文章目录
离散化介绍及模板
当题目中数据范围很⼤,但是数据的总量不是很⼤,并且我们需要⽤数据的值来映射数组的下标时,直接映射大概率会失败,因为无法开辟很大容量的空间。此时我们就可以⽤离散化的思想先预处理⼀下所有的数据,使的每⼀个数据都映射成⼀个范围较小的值。
比如: [9, 99, 9999, 999999] 离散之后就变成 [1, 2, 3, 4] ,所以离散听起来高大上,本质就是一种映射。
对于用离散化预处理数据,小编下面介绍两种模板:
模板一:排序+去重+二分查找首先用两个数组a[N],d[N]存储原数据,d[N]用来进行排序+去重操作,首先用algorithm的sort排序,然后用algorithm的unique去重,unique的参数传递和sort一样,返回值是去重后数组的最后一个元素的下一个位置。
然后用二分查找找指定数据在d[N]对应的下标,d[N]对应的下标即为映射后的范围较小的值。
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int n; //原数据个数
int pos; //去重后数据个数
int a[N]; //原数据
int d[N]; //离散化后的数据
//二分查找原数据在离散化后所在数组的下标,即为离散化后的值
int find(int a)
{
int l = 1, r = pos;
int mid = 0;
while (l < r)
{
mid = (l + r) / 2;
if (d[mid] >= a)
{
//结果是中点或在中点左边
r = mid;
}
else
{
//结果在中点右边
l = mid + 1;
}
}
return l;
}
int main()
{
cin >> n;
//初始化原数据
for (int i = 1; i <= n; i++)
{
cin >> a[i];
d[i] = a[i];
}
//排序
sort(d + 1, d + 1 + n);
//去重 + 计算去重后的数据个数
pos = unique(d + 1, d + 1 + n) - (d + 1);
//输出结果
for (int i = 1; i <= n; i++)
{
cout << a[i] << "离散化后:" << find(a[i]) << endl;
}
return 0;
}模板二:排序+哈希表去重和确定最终位置
整体实现和模板一相似,主要区别在去重和确定最终位置上,除了a[N]存放原数据和d[N]存放排序后的数据外,还需要一个unordered_map对象id来确定离散后的位置,k,v分别是<原始的值,离散之后的值>,实现思路是遍历排序后的数组,遇到没存过的数据直接将它的原始数据和离散后的数据存入id,遇到存过的直接continue。后面要使用离散后的值直接拿着原始值到id中查即可,不用像将离散后的值存在数组中需要拿着原始值通过查找算法找到对应的数组下标。
cpp
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 1e5 + 10;
int n; //原数据个数
int a[N]; //原数据
int d[N]; //排序后的数据
unordered_map<int, int> id; //<原始的值,离散之后的值>
int main()
{
cin >> n;
//初始化原数据
for (int i = 1; i <= n; i++)
{
cin >> a[i];
d[i] = a[i];
}
//排序
sort(d + 1, d + 1 + n);
//利用哈希表去重+记录映射后位置
int cnt = 1; //记录当前元素是第几号元素
for (int i = 1; i <= n; i++)
{
int x = d[i];
if (id.count(x))
{
//已经存过了,直接continue
continue;
}
id[x] = cnt++;
}
//输出结果
for (int i = 1; i <= n; i++)
{
cout << a[i] << "离散化后:" << id[a[i]] << endl;
}
return 0;
}火烧赤壁
题目描述
题目解析
本题解题思路是离散化+差分,首先要统计被烧的区间长度,本质就是利用一个初始化为0的数组,若被烧就将对应的区间在数组中的数据整体加1,最后统计数组中不为0的数据个数即为被烧长度,而将数组中的一段区间整体加上一个数就可以用差分来处理。
然后因为本题的数据范围较大,直接用原数据进行差分空间不够,所以需要先将原数据离散化为较小的值,然后用较小的值进行差分,最后再通过离散后的值找到离散前的值统计最终长度。
注意:本题需要对离散化模板进行一定改进,在利用哈希表去重+离散时需要事先将排序后的数组进行去重操作,然后进行离散化,目的是为了解决最后通过离散化后的数据找离散化前的数据时:ret += d[j] - d[i]; ,d[j]、d[i]中的 i j 表面上是离散化后的数据,但是它们本质是排序后的数组下标,以下面这个排序后的数组为例: (-1,-1, 4, 5, 9)比如我们要找这个数组中的4,是通过d[2]找到的,但是如果不提前去重,d[2]就会找到-1。
代码
cpp
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
const int N = 2e4 + 10;
int n;
int a[N], b[N]; //原左端点,右端点数据
int pos; //标记d数组初始化数据时的下标
int cnt; //标记去重后的元素个数
int d[2 * N]; //排序后的数据
unordered_map<int, int> id; //<原数据, 离散后的数据>
int f[2 * N]; //差分数组
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i] >> b[i];
d[++pos] = a[i], d[++pos] = b[i];
}
//排序 + 提前去重
sort(d + 1, d + 1 + pos);
cnt = unique(d + 1, d + 1 + pos) - (d + 1);
int p = 0; //用来初始化离散值
//利用哈希表离散
for (int i = 1; i <= cnt; i++)
{
id[d[i]] = ++p;
}
// 将离散后的数据进行差分
for (int i = 1; i <= n; i++)
{
int l = id[a[i]], r = id[b[i]];
f[l]++;
f[r]--; //因为题目区间本身左闭右开,所以这里不用r-1
}
//将差分数组进行还原
for (int i = 1; i <= cnt; i++)
{
f[i] = f[i] + f[i - 1];
}
//利用还原后的离散数据找到原数据统计最终长度
int ret = 0; //燃烧长度总和
for (int i = 1; i <= cnt; i++)
{
//遍历还原后的差分数组
int j = i;
while (j <= cnt && f[j])//找到一段不为0的区间,i为起点,j为终点
j++;
ret += d[j] - d[i];
i = j;
}
cout << ret << endl;
return 0;
}贴海报
题目描述
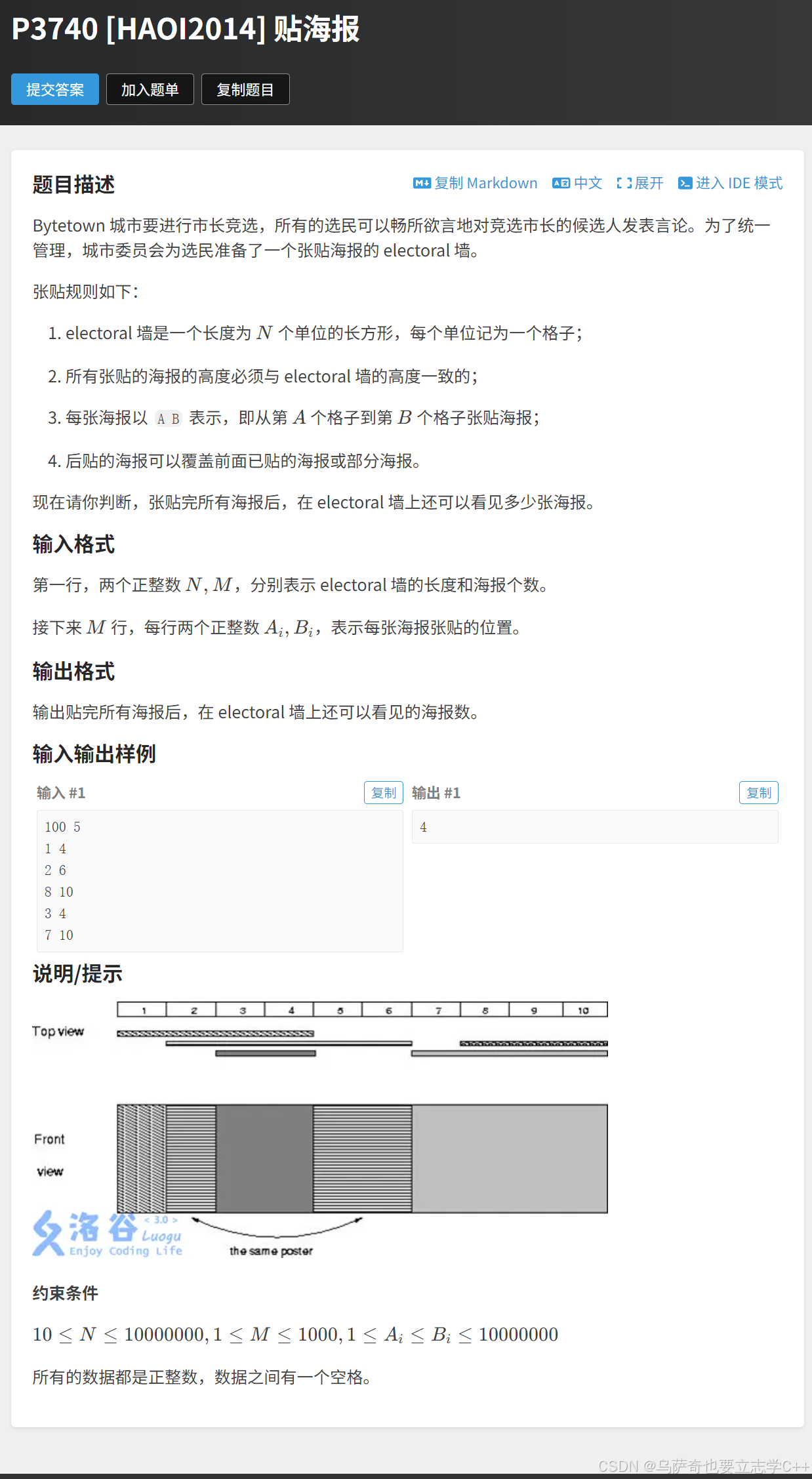
题目解析
本题首先理解题意,要求墙上还可以看见的海报数,我们把数组当作墙,不同的数值当作不同的海报,本质就是求数组中有多少个不同的数,张贴海报就是覆盖式的修改数组中一段区间的值,张贴海报需要两层for循环,一层遍历所有海报,一层模拟粘贴海报:遍历海报的左右区间并赋值,最坏的情况是1e4 * 1e8,必然会超时,所以需要将区间左右端点值离散化。 首先小编先提出一个需要注意的点,本题不能直接按照模板进行离散化,例如区间[2 5] [2 3] [5 6],直接进行离散化结果是2,但是其实结果是3,因为直接离散化会出现区间端点的覆盖情况, 比如这里的5同时属于 [2,5] 和 [5,6],离散后丢失中间间隔解决办法就是除了将区间左右端点离散化,还需要将左右端点各自加1的值离散化。
最后统计结果利用set,因为set有去重功能。
代码
cpp
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
using namespace std;
const int N = 1010;
int a[N], b[N]; //海报起始位置,终止位置
int pos; //标记去重前海报
int d[4 * N]; //存储所有海报
int cnt; //标记去重后海报
int post[4 * N]; //模拟墙面,存储每个位置被哪张海报覆盖
unordered_map<int, int> id; //原数据,离散后数据
unordered_set<int> ret; //统计可以看见的海报数
int main()
{
int m, n;
cin >> n >> m;
for (int i = 1; i <= m; i++)
{
cin >> a[i] >> b[i];
d[++pos] = a[i];
d[++pos] = b[i];
d[++pos] = a[i] + 1;
d[++pos] = b[i] + 1;
}
//排序
sort(d + 1, d + 1 + pos);
//利用哈希表去重 + 离散
for (int i = 1; i <= pos; i++)
{
int x = d[i];
if (id.count(x))
continue;
id[x] = ++cnt;
}
//模拟张贴海报
for (int i = 1; i <= m; i++)
{
int l = id[a[i]], r = id[b[i]];
for (int j = l; j <= r; j++)
{
post[j] = i;
}
}
//统计post数组中有多少个不同的值,即为答案
for (int i = 1; i <= cnt; i++)
{
if (!post[i] || ret.count(post[i])) //post[i]为0或已经存入ret直接continue
continue;
ret.insert(post[i]);
}
cout << ret.size() << endl;
return 0;
}以上就是小编分享的全部内容了,如果觉得不错还请留下免费的关注和收藏如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
