[机器学习-从入门到入土] 拓展-范数
个人导航
知乎:https://www.zhihu.com/people/byzh_rc
CSDN:https://blog.csdn.net/qq_54636039
注:本文仅对所述内容做了框架性引导,具体细节可查询其余相关资料or源码
参考文章:各方资料
文章目录
- [[机器学习-从入门到入土] 拓展-范数](#[机器学习-从入门到入土] 拓展-范数)
- 个人导航
- 范数
-
-
-
- [L 0 L_0 L0范数 (严格来说不是范数)](#L 0 L_0 L0范数 (严格来说不是范数))
- [L 1 L_1 L1范数](#L 1 L_1 L1范数)
- [L 2 L_2 L2范数](#L 2 L_2 L2范数)
- [L p L_p Lp范数](#L p L_p Lp范数)
- 范数的等值线
-
-
范数
设向量
x = ( x 1 , x 2 , ... , x d ) ∈ R d x=(x_1,x_2,\dots,x_d)\in\mathbb{R}^d x=(x1,x2,...,xd)∈Rd
L 0 L_0 L0范数 (严格来说不是范数)
非零元素的个数:
∥ x ∥ 0 = # { i ∣ x i ≠ 0 } \|x\|_0 = \#\{i \mid x_i \neq 0\} ∥x∥0=#{i∣xi=0}
( 某个集合 ) \#(\text{某个集合}) #(某个集合): 表示集合中元素的个数
- 直接度量稀疏性 -> 理论上的"理想稀疏约束"
- 不关心数值大小,只关心"是不是 0"
优化性质:
- ❌ 非凸
- ❌ 非连续
- ❌ NP-hard(组合优化)
L 1 L_1 L1范数
稀疏性的凸替身
∥ x ∥ 1 = ∑ i = 1 d ∣ x i ∣ \|x\|1=\sum{i=1}^d |x_i| ∥x∥1=i=1∑d∣xi∣
优化性质:
- ✅ 凸
- ❌ 不光滑(0 点不可导)
典型用途:
-
Lasso 回归
min w ∥ y − X w ∥ 2 2 + λ ∥ w ∥ 1 \min_w \|y-Xw\|_2^2+\lambda\|w\|_1 minw∥y−Xw∥22+λ∥w∥1
L 2 L_2 L2范数
能量与稳定性
∥ x ∥ 2 = ( ∑ i = 1 d x i 2 ) 1 / 2 \|x\|2=\left(\sum{i=1}^d x_i^2\right)^{1/2} ∥x∥2=(i=1∑dxi2)1/2
优化性质:
- ✅ 凸
- ✅ 光滑
- ✅ 强凸(数值稳定)
典型用途:
-
Ridge 回归 (岭回归)
min w ∥ y − X w ∥ 2 2 + λ ∥ w ∥ 2 2 w \min_w \|y-Xw\|_2^2+\lambda\|w\|_2^2w minw∥y−Xw∥22+λ∥w∥22w
L p L_p Lp范数
∥ x ∥ p = ( ∑ i = 1 d ∣ x i ∣ p ) 1 / p , p ≥ 1 \|x\|p = \left(\sum{i=1}^d |x_i|^p\right)^{1/p},\quad p\ge 1 ∥x∥p=(i=1∑d∣xi∣p)1/p,p≥1
- p p p 越小 → 越稀疏,但越难优化
- p p p 越大 → 越平滑,但越不稀疏
严格意义上,只有 p ≥ 1 p\ge 1 p≥1 时才是"范数"
| p | 几何形状 | 性质 |
|---|---|---|
| p = 1 p=1 p=1 | 菱形 | 强稀疏 |
| 1 < p < 2 1<p<2 1<p<2 | 圆角菱形 | 稀疏 + 稳定 |
| p = 2 p=2 p=2 | 圆 | 平滑、稳定 |
| p → ∞ p\to\infty p→∞ | 正方形 | 控制最大分量 |
极限情形:
- p → 0 p\to 0 p→0:趋近 L 0 L_0 L0
- p → ∞ p\to\infty p→∞: ∥ x ∥ ∞ = max i ∣ x i ∣ \|x\|_\infty=\max_i |x_i| ∥x∥∞=maxi∣xi∣
| 范数 | 是否凸 | 是否光滑 | 是否产生稀疏 | 典型角色 |
|---|---|---|---|---|
| L 0 L_0 L0 | ❌ | ❌ | ⭐⭐⭐⭐⭐ | 理想目标 |
| L 1 L_1 L1 | ✅ | ❌ | ⭐⭐⭐⭐ | 稀疏替代 |
| L 2 L_2 L2 | ✅ | ✅ | ⭐ | 稳定正则 |
| L n L_n Ln | n > 1 n>1 n>1 ✅ | n > 1 n>1 n>1 ✅ | 递减 | 折中方案 |
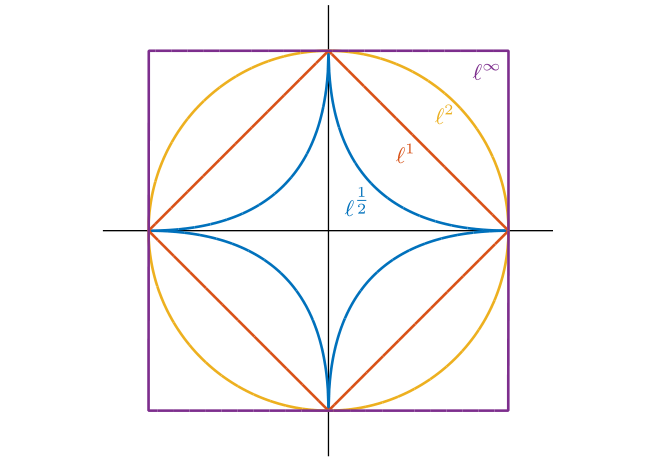
范数的等值线
在二维情况下: x = ( x 1 , x 2 ) ∈ R 2 x=(x_1,x_2)\in\mathbb{R}^2 x=(x1,x2)∈R2
范数的等值线:
- ∥ x ∥ p = 1 \|x\|_p = 1 ∥x∥p=1:一条曲线
- ∥ x ∥ p ≤ 1 \|x\|_p \le 1 ∥x∥p≤1:这条曲线围成的区域
各范数的情况:
- L 0 L_0 L0: x轴与y轴
(当y有值时x=0, 当x有值时y=0) - L 1 L_1 L1: 菱形
(顶点是 ( − 1 , 0 ) , ( 1 , 0 ) , ( 0 , 1 ) , ( 0 , − 1 ) (-1,0),(1,0),(0,1),(0,-1) (−1,0),(1,0),(0,1),(0,−1)) - L 2 L_2 L2: 圆
(经过 ( − 1 , 0 ) , ( 1 , 0 ) , ( 0 , 1 ) , ( 0 , − 1 ) (-1,0),(1,0),(0,1),(0,-1) (−1,0),(1,0),(0,1),(0,−1))