leetcode 1458. 两个子序列的最大点积困难

给你两个数组 nums1 和 nums2 。

请你返回 nums1 和 nums2 中两个长度相同的非空子序列的最大点积。

数组的非空子序列是通过删除原数组中某些元素（可能一个也不删除）后剩余数字组成的序列，但不能改变数字间相对顺序。比方说，[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。

示例 1：

复制代码

输入：nums1 = [2,1,-2,5], nums2 = [3,0,-6]
输出：18
解释：从 nums1 中得到子序列 [2,-2] ，从 nums2 中得到子序列 [3,-6] 。
它们的点积为 (2*3 + (-2)*(-6)) = 18 。

示例 2：

复制代码

输入：nums1 = [3,-2], nums2 = [2,-6,7]
输出：21
解释：从 nums1 中得到子序列 [3] ，从 nums2 中得到子序列 [7] 。
它们的点积为 (3*7) = 21 。

示例 3：

复制代码

输入：nums1 = [-1,-1], nums2 = [1,1]
输出：-1
解释：从 nums1 中得到子序列 [-1] ，从 nums2 中得到子序列 [1] 。
它们的点积为 -1 。

提示：

1 <= nums1.length, nums2.length <= 500
-1000 <= nums1[i], nums2[i] <= 1000

点积：

复制代码

定义 a = [a1, a2,..., an] 和b = [b1, b2,..., bn] 的点积为：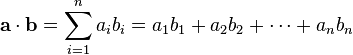

复制代码

这里的 Σ 指示总和符号。

分析：动态规划，令 dp[i][j] 代表 nums1 前 i 个数，nums2 前 j 个数这两个子序列可以取得的最大点积，可初始化 dp 数组的第一行和第一列为：

dp[1][1]=nums1[0]*nums2[0]，

dp[1][i]=max(dp[1][i-1]，nums1[0]*nums2[i-1])，

dp[i][1]=max(dp[i-1][1]，nums1[i-1]*nums2[0])。

这里代表其中一个数组只取第一个数，另一个数组逐渐取到所有数时可以获得的最大子序列点积。当 i 和 j 都大于 1 时， dp[i][j] 可以由 dp[i-1][j]，dp[i][j-1]，以及 dp[i-1][j-1] 转移而来，具体来说，即 nums1 前 i 个数，nums2 前 j 个数这两个子序列可以取得的最大点积，要么是：

nums1 前 i-1 个数，nums2 前 j 个数的最大点积，或者

nums1 前 i 个数，nums2 前 j-1 个数的最大点积，或者

nums1 前 i-1 个数，nums2 前 j-1 个数的最大点积加上 nums[i]*nums[j]。

可得转移方程：dp[i][j]=max(dp[i-1][j-1]+nums1[i-1]*nums2[j-1],max(dp[i-1][j],dp[i][j-1]))

注意如果 dp[i-1][j-1] 小于零，而 nums1[i-1]*nums2[j-1] 大于 0，那么转移方程中 dp[i-1][j-1]+nums1[i-1]*nums2[j-1] 就要变成 nums1[i-1]*nums2[j-1]。

cpp 复制代码

int maxDotProduct(int* nums1, int nums1Size, int* nums2, int nums2Size) {
    int ans=0;
    int dp[510][510];
    for(int i=0;i<=500;++i)
        for(int j=0;j<=500;++j)
            dp[i][j]=0;
    dp[1][1]=nums1[0]*nums2[0];
    for(int i=2;i<=nums2Size;++i)
        dp[1][i]=fmax(dp[1][i-1],nums1[0]*nums2[i-1]);
    for(int i=2;i<=nums1Size;++i)
        dp[i][1]=fmax(dp[i-1][1],nums1[i-1]*nums2[0]);
    
    for(int i=2;i<=nums1Size;++i)
    {
        for(int j=2;j<=nums2Size;++j)
        {
            int sum=nums1[i-1]*nums2[j-1];
            if(sum>0&&dp[i-1][j-1]<0)dp[i][j]=fmax(sum,fmax(dp[i-1][j],dp[i][j-1]));
            else dp[i][j]=fmax(dp[i-1][j-1]+sum,fmax(dp[i-1][j],dp[i][j-1]));
        }
    }

    return dp[nums1Size][nums2Size];
}

leetcode 1458. 两个子序列的最大点积 困难

leetcode 1458. 两个子序列的最大点积困难