在机器学习实践中,我们每天都在和数据打交道:加载数据集、清洗数据、训练模型、评估指标。
但有一个问题,几乎所有初学者,甚至不少工程师都会下意识忽略 :你的数据集,从来都不是"全部世界",它只是一个样本。
在机器学习和数据分析中,抽样策略 往往比模型结构更早决定结论是否可信。这一篇,我们不再讨论"为什么要抽样",而是直接进入核心问题:不同的抽样方式,会把你带向完全不同的世界。
本节讨论的五种抽样方式,几乎覆盖了现实世界中所有数据来源的原型。
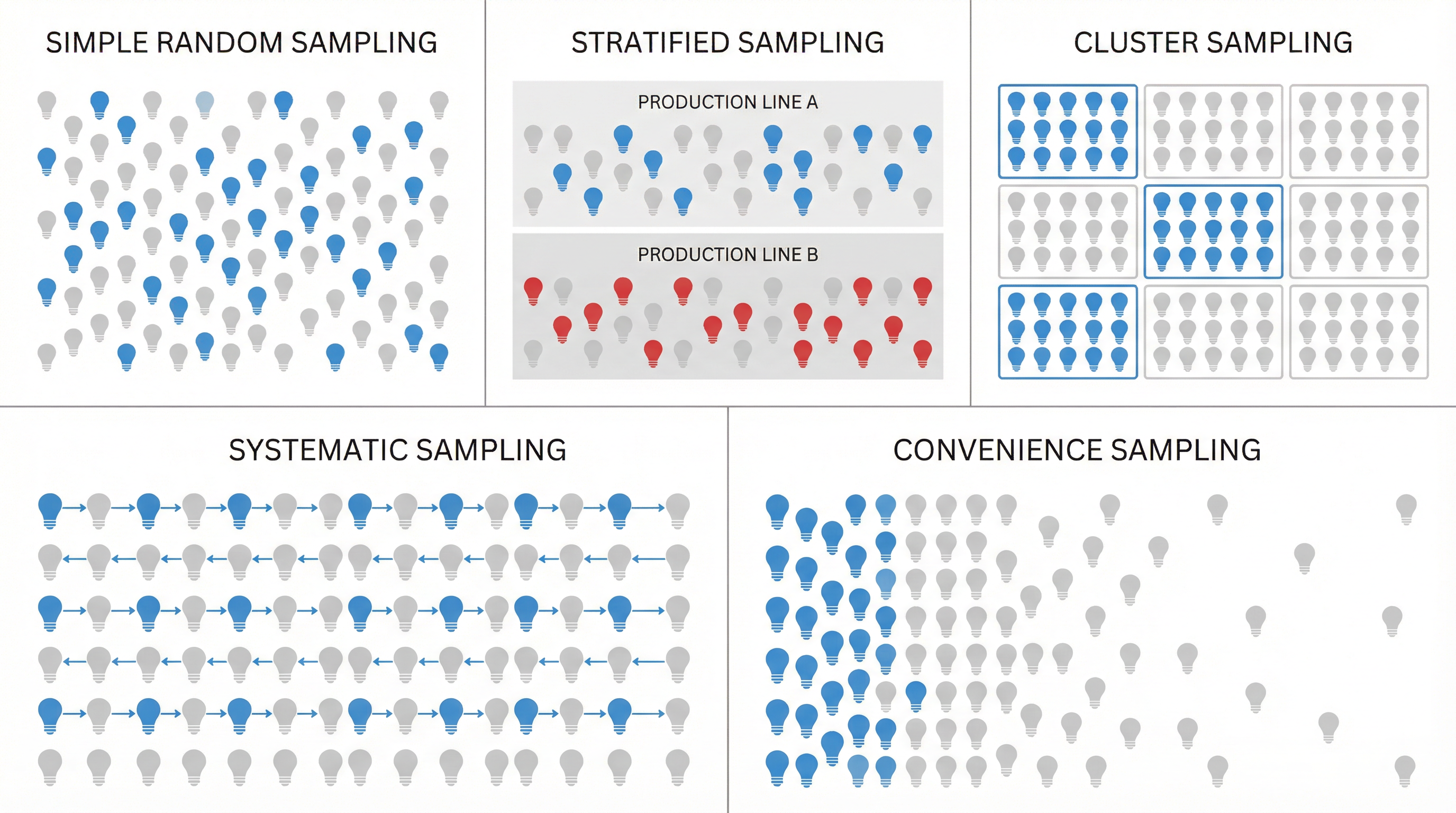
一、抽样问题的工程化表述
沿用灯泡工厂的例子(上一篇已经介绍过背景):
1.1 背景
设今年共生产灯泡 N=1,000,000N = 1{,}000{,}000N=1,000,000 个,其真实平均使用寿命记为总体参数 μ\muμ,但是该参数属于总体层面,无法直接观测。
1.2 工程约束
由于寿命测试具有破坏性,实验与成本条件限制我们最多只能对n=1000n=1000n=1000个灯泡进行测试。因此,对总体参数 μ\muμ 的认知只能建立在样本之上。
1.3 推断目标
在统计意义上,这一问题属于有限样本条件下的参数推断问题。
而在工程实践中,问题的关键并不在于参数估计公式的选择,而在于样本是通过何种抽样机制从总体中生成的。
不同的抽样机制对应不同的样本分布假设,并将直接影响估计量的无偏性、方差以及由此得出的结论是否可靠。
二、简单随机抽样(Simple Random Sampling)
2.1 抽样机制定义
简单随机抽样(Simple Random Sampling, SRS)指的是:在抽样过程中,总体中的每一个个体都具有完全相同的被选中概率,且样本的产生不依赖于任何额外的结构信息或分组假设。
在形式上,这等价于从规模为NNN的总体中,以均匀分布、无放回地抽取nnn个个体作为样本。
2.2 在灯泡工厂问题中的实现方式
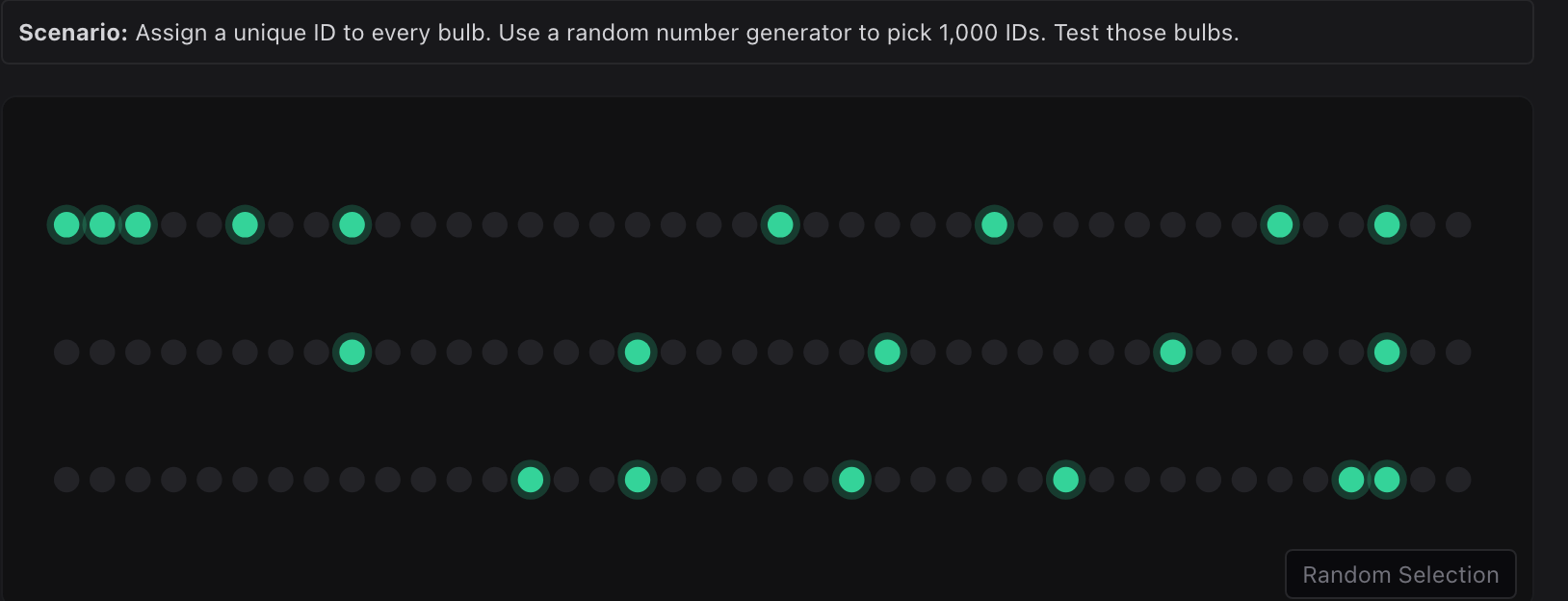
在灯泡工厂的设定下,简单随机抽样要求能够对每一个灯泡进行等概率访问。这通常意味着需要为每个灯泡建立唯一标识,并借助随机数生成机制,从全部生产灯泡中随机选取n=1000n=1000n=1000 个进行寿命测试。
该过程假设抽样操作本身不会引入任何与灯泡质量相关的系统性因素。
2.4 统计性质与理论地位
由于样本是通过理想化的随机机制产生的,简单随机抽样在统计理论中占据基础性地位。在该抽样假设下,常见统计量(如样本均值)通常具有良好的理论性质,包括无偏性以及可解析的方差表达形式。
正因如此,许多统计推断结论以及机器学习中的理论分析,都会默认训练数据来源满足简单随机抽样或近似满足独立同分布(IID)的假设。
2.4 工程可行性与现实代价
尽管简单随机抽样在理论上具有诸多优点,但在工程实践中往往难以严格实现。该方法要求完整、可索引的抽样框,并且需要能够在实际系统中对任意个体进行等概率访问。
在大规模生产环境、在线系统或数据流场景下,这种访问条件通常难以满足,从而迫使工程实践采用对简单随机抽样的各种近似或替代方案。
2.5 在机器学习中的对应关系
在机器学习语境下,简单随机抽样对应于经典的 IID 数据假设。模型的泛化分析、误差界推导以及许多正则化理论,均建立在这一假设或其近似成立的前提之上。
当真实数据的生成机制显著偏离简单随机抽样时,这些理论结论的适用性也需要重新审视。
三、分层抽样(Stratified Sampling)
3.1 抽样机制定义
分层抽样(Stratified Sampling)是一种在已知总体结构信息的前提下进行的抽样方法。其核心思想是:根据某些关键属性将总体划分为若干互不重叠的子总体(层),然后在每一个层内分别进行随机抽样。
在形式上,分层抽样可以被视为对简单随机抽样的结构化扩展:随机性仍然存在,但被限定在每一个预先定义的层内部。
3.2 在灯泡工厂问题中的实现方式
在灯泡工厂的例子中,假设我们已知不同生产线在全年产量中所占的比例,例如:
- A 生产线占总产量的 70%
- B 生产线占总产量的 30%
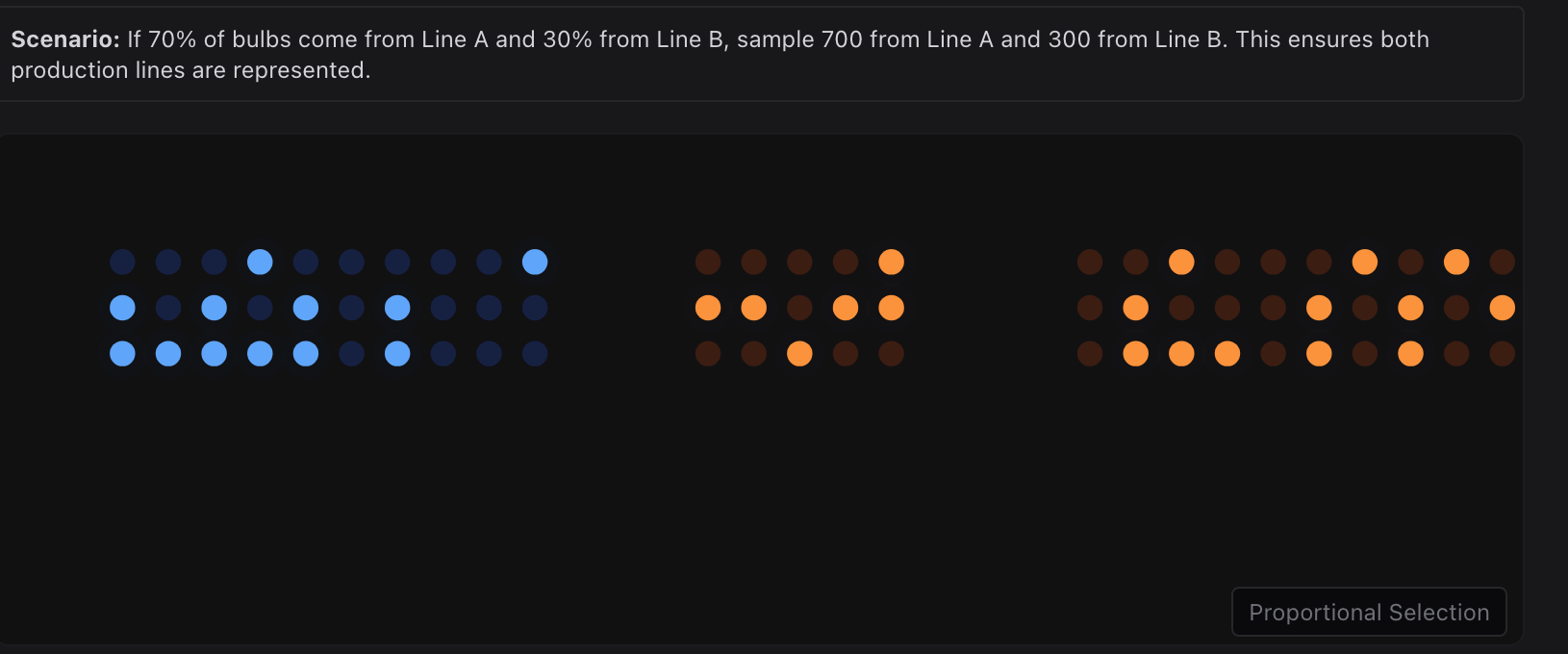
在这种情况下,可以先按生产线对总体进行分层,然后分别从 A、B 两个层中随机抽取样本,例如从 A 线抽取 700 个灯泡,从 B 线抽取 300 个灯泡进行寿命测试。
这一过程保证了样本在生产线维度上的组成结构与总体保持一致。
3.3 统计性质与潜在优势
相较于不加区分的简单随机抽样,分层抽样在统计上具有一个重要优势:当层内个体相对同质、层间差异较大时,分层抽样通常能够显著降低估计量的方差。
直观地说,通过在每一个关键子群体中分别进行抽样,可以避免由于样本偶然性导致某些群体被过度或不足表示,从而提升估计结果的稳定性与精度。
3.4 前提条件与潜在风险
分层抽样的有效性依赖于一个关键前提:分层所依据的属性必须与研究目标高度相关。
如果分层维度选择不当,或者忽略了真正重要的异质性来源,那么分层抽样不仅无法降低方差,反而可能引入新的系统性偏差。此外,分层抽样要求在抽样之前能够获得可靠的分层信息,这在某些工程场景下本身就是一项不小的成本。
3.5 在机器学习中的对应关系
在机器学习实践中,分层抽样是一种极为常见的数据处理策略。
-
例如:
- 在类别不平衡问题中,常通过分层抽样确保各类别在训练集和测试集中均有充分代表;
- 在数据集划分阶段,采用分层的 train / test 划分以保持标签分布一致;
- 在用户行为建模中,按关键用户属性进行分层以减少采样偏差。
-
这些做法本质上都是在利用已知结构信息,对简单随机抽样进行修正,以获得更具代表性的样本。
3.6 小结
分层抽样通过引入结构性先验信息,在保持随机性的同时提高了样本的代表性和估计精度。然而,这一方法并非"无条件更优",其效果高度依赖于分层维度的合理性。
在实践中,分层抽样体现了一种典型的工程权衡:用对数据结构的先验认知,换取更低的统计不确定性。
四、整群抽样(Cluster Sampling)
4.1 抽样机制定义
整群抽样(Cluster Sampling)是一种以"自然形成的群体"为基本抽样单位的方法。在该机制下,总体首先被划分为若干互不重叠的群体(cluster),随后随机抽取部分群体,并将被选中群体中的所有个体全部纳入样本。
与分层抽样不同,整群抽样的随机性作用于"群体层面",而非个体层面。
4.2 在灯泡工厂问题中的实现方式
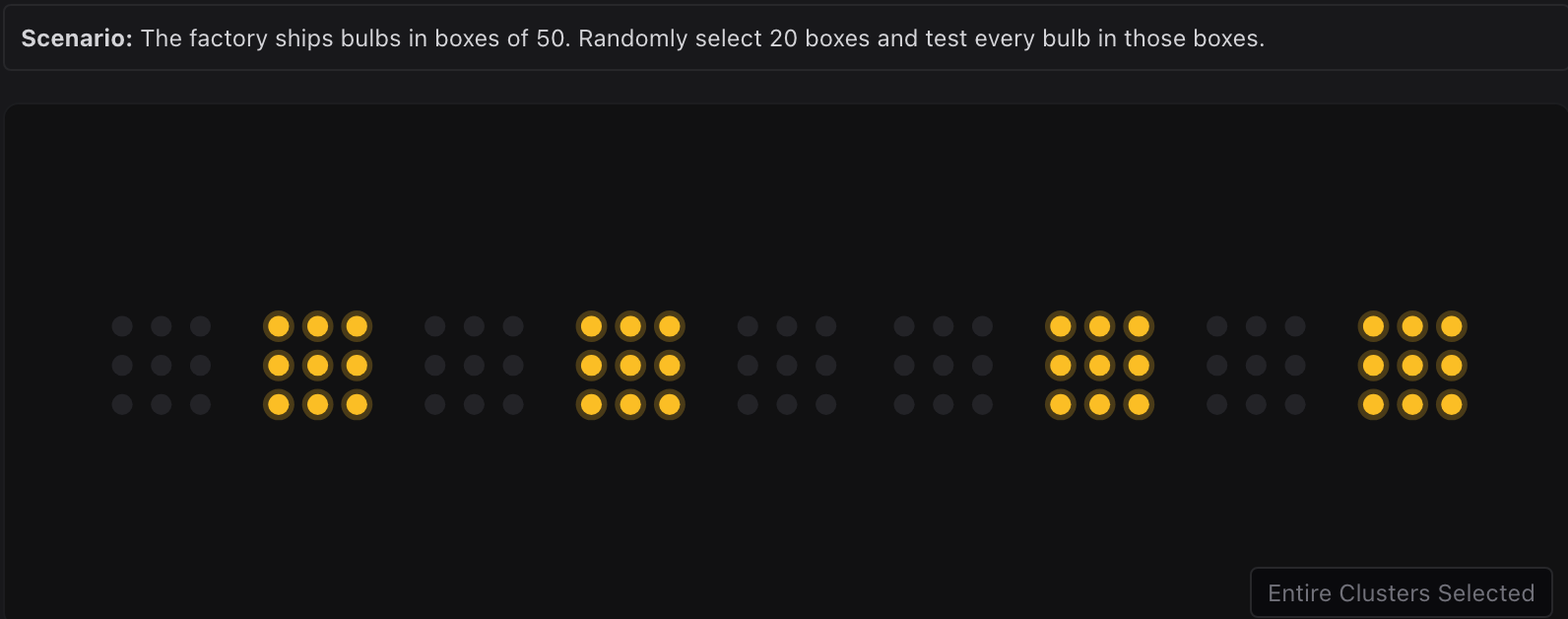
在灯泡工厂的例子中,假设灯泡以每盒505050个的形式进行包装与流转。此时,每一盒灯泡可被视为一个自然群体。
整群抽样的实施方式是:随机抽取若干盒灯泡(例如202020盒),并对这些盒子中的所有灯泡进行寿命测试。由此得到的样本规模为20×50=100020 \times 50 = 100020×50=1000。
该过程显著简化了抽样操作,因为测试单位从"单个灯泡"转变为"整盒灯泡"。
4.3 工程优势与现实动机
整群抽样在工程实践中的主要优势在于其较低的实施成本与较高的操作可行性。由于抽样和测试都以群体为单位进行,该方法通常能够显著减少物流、管理以及抽样过程本身的复杂度。
正因如此,整群抽样在工业生产、现场调查以及大规模系统监控中被广泛采用。
4.4 隐含假设与统计风险
整群抽样的有效性依赖于一个极其关键、却往往被忽略的隐含假设:每一个群体在统计意义上,都是总体的一个近似缩影。
一旦这一假设不成立,例如群体内部高度同质、群体之间存在显著差异,那么样本将严重偏离总体分布。由于整群抽样在群体层面"整体纳入",这种偏差往往会被成倍放大,而非被随机性所抵消。
因此,相较于简单随机抽样或分层抽样,整群抽样通常具有更高的估计方差和更大的偏差风险。
4.5 在机器学习中的高频风险场景
在机器学习实践中,整群抽样的风险尤为常见,其典型表现包括:
- 按用户、设备或城市采样数据;
- 按时间窗口或批次收集日志数据;
- 在训练与评估阶段未能正确处理群体依赖结构。
这些场景下,如果同一群体的数据同时出现在训练集与测试集中,极易引发 group leakage ,从而导致模型性能被系统性高估。此外,模型可能过度拟合群体特征而非真正具有泛化能力的信号,形成 group bias。
4.6 小结
整群抽样通过牺牲个体层面的随机性,换取了工程上的便利性与成本优势。然而,这种便利并非免费,其代价是对"群体可代表总体"这一假设的高度依赖。
在实践中,整群抽样是一种工程驱动型抽样策略,其使用前提必须经过慎重评估,否则将成为系统性偏差的重要来源。
五、系统抽样(Systematic Sampling)
5.1 抽样机制定义
系统抽样(Systematic Sampling)是一种在总体排序后,按照固定间隔规则选取样本的抽样方法。
其典型流程为:在总体中随机确定一个起始位置,然后按照固定步长kkk(如每隔kkk个个体)依次抽取样本,直至达到预定样本规模。
5.2 在灯泡工厂问题中的实现方式
在灯泡工厂场景中,假设灯泡按照生产顺序依次下线并编号。
若需要抽取n=1000n=1000n=1000个样本,可以设定抽样间隔为每100010001000个灯泡抽取 1 个,并随机确定第一个抽样位置。这种方式避免了为每个个体生成随机数,抽样过程高度规则化,极易实现自动化。

5.3 工程优势
系统抽样的主要优势在于其操作简单、成本低、可重复性强。
在许多工业流水线或在线系统中,系统抽样几乎不需要额外的抽样框构建成本,非常适合流式数据或持续生成的数据场景。
5.4 隐含假设与潜在风险
系统抽样的风险来自于一个关键前提:总体的排列顺序本身不应与目标变量存在周期性或结构性关联。
一旦总体顺序与某些潜在模式高度相关(例如生产批次、设备轮换、时间周期),固定步长的抽样方式可能会系统性地遗漏或重复某类样本,从而引入难以察觉的偏差。
这种偏差并非由样本量不足导致,而是由抽样机制本身的结构性缺陷引入。
5.5 机器学习中的典型对应
在机器学习中,系统抽样的影子几乎无处不在,例如:
- 按时间顺序每隔kkk条日志采样;
- 从排序后的数据集中按固定步长切分训练样本;
- 未打乱顺序直接进行 mini-batch 构建。
在这些场景中,若数据顺序本身携带信息(时间趋势、用户行为阶段、系统状态变化),系统抽样可能导致模型学习到错误的统计结构。
5.6 小结
系统抽样是一种高度工程友好的抽样方式,但其安全性严重依赖于数据顺序的"无信息性"。在机器学习任务中,若忽略这一前提,该方法极易成为隐蔽偏差的来源。
六、便利抽样(Convenience Sampling)
6.1 抽样机制定义
便利抽样(Convenience Sampling)是指样本并非通过随机机制产生,而是基于获取成本、可用性或操作便利性直接收集。
在统计学中,这是一种非概率抽样方法,其样本生成机制通常无法用明确的概率模型描述。
6.2 在灯泡工厂问题中的实现方式
在灯泡工厂场景中,便利抽样可能表现为:
-
只测试库存中现成的灯泡;
-
只抽取某一天、某一班次的产品;
-
只选择容易接触或运输的批次进行测试。
这些样本并非从总体中"被抽中",而是"刚好在手边"。
6.3 工程动机
便利抽样在现实工程中极为常见,其背后动机非常直接:
-
成本最低;
-
速度最快;
-
操作门槛几乎为零。
在资源受限或快速迭代的场景下,便利抽样往往成为默认选择。
6.4 统计后果
便利抽样的根本问题在于:样本分布完全由采集路径决定,而非由总体决定。
由于抽样概率未知,甚至在个体层面不可定义,基于便利样本进行的统计推断通常缺乏严格的理论保证。任何看似"合理"的估计结果,都可能只是采样偏差的产物。
6.5 在机器学习中的现实映射
在机器学习实践中,便利抽样几乎是最常见、也最危险的数据来源:
- 只使用"已有日志"训练模型;
- 用线上曝光数据替代真实用户分布;
- 用易获取的公开数据集推断真实业务场景。
这类做法往往在离线评估阶段表现良好,但一旦部署到真实环境,模型性能迅速退化,其根源正是训练数据与目标分布之间的系统性偏差。
6.6 小结
便利抽样并非"错误",但它从来不是中性的。一旦使用便利样本,所有后续分析都必须明确承认其适用范围与局限性,否则模型性能与统计结论都将失去可信基础。
七、总结:抽样方式决定你能相信什么
从简单随机抽样到分层、整群、系统与便利抽样,每一种方法都隐含着不同的统计假设与工程取舍。
在机器学习中,模型从不直接面对"世界本身",而只能看到被抽样机制过滤后的现实。理解抽样方式,等价于理解模型认知边界的来源。