本节再详细讲解下地面约束的理论跟具体实现,本节以ceres-solver的解析雅克比进行验证,接下来情况具体实现;
一. 问题描述


二. 数学推导






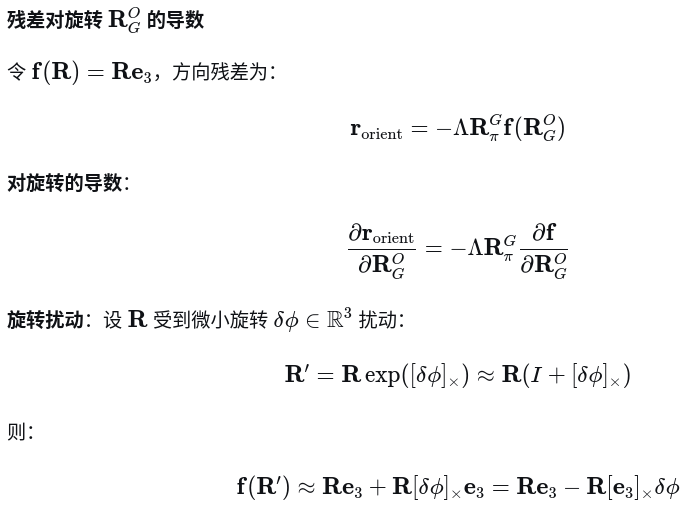
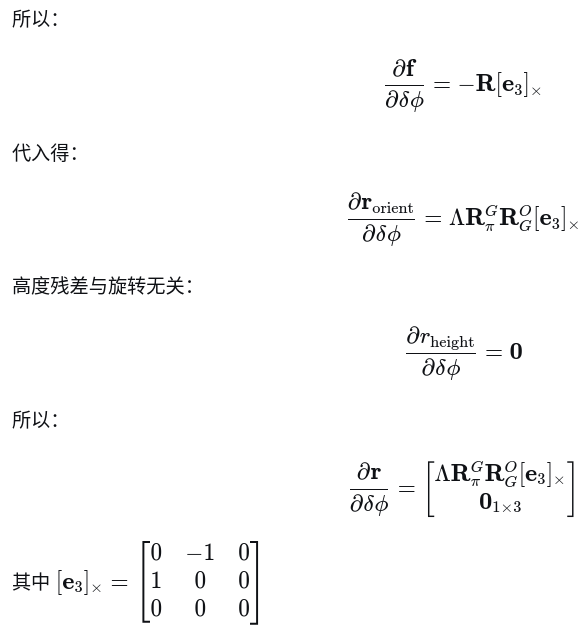



二.结果展示
bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const override {
Eigen::Map<const Eigen::Matrix<double, 3, 1>> p_a(parameters[0]);
Eigen::Map<const Eigen::Quaterniond> q_a(parameters[1]);
const Eigen::Matrix<double, 3, 3> G_R_O = q_a.toRotationMatrix();
const Eigen::Matrix<double, 3, 1> G_p_O = p_a;
// 提取平面参数
const Eigen::Matrix<double, 3, 3> pi_R_G = Eigen::Matrix<double, 3, 3>::Identity();
const double pi_z_G = 0.0;
// 选择矩阵:取向量的前两个分量
Eigen::Matrix<double, 2, 3> Lambda;
Lambda << 1.0, 0.0, 0.0,
0.0, 1.0, 0.0;
// Z 轴单位向量
const Eigen::Matrix<double, 3, 1> e3(double(0.0), double(0.0), double(1.0));
Eigen::Map<Eigen::Matrix<double, 3, 1>> residual(residuals);
// 前两个残差:方向约束
// O 坐标系的 Z 轴在平面坐标系下的投影应该为零(即与平面法线对齐)
residual.head<2>() = -Lambda * pi_R_G * G_R_O * e3;
// 第三个残差:高度约束
// 位姿原点在平面法线方向上的投影应该等于平面高度
residual[2] = pi_z_G + e3.transpose() * pi_R_G * G_p_O;
residual = sqrt_information_ * residual;
if (!jacobians) return true;
auto skew = [](const Eigen::Vector3d& v) -> Eigen::Matrix3d {
Eigen::Matrix3d S;
S << 0., -v.z(), v.y(),
v.z(), 0., -v.x(),
-v.y(), v.x(), 0.;
return S;
};
// 注意:这里使用左乘的so(3)表示,因为残差前两行与旋转有关
if (jacobians[0]) {
Eigen::Map<Eigen::Matrix<double, 3, 3>, Eigen::RowMajor> jacobian_pos(jacobians[0]);
Eigen::Matrix<double, 3, 3> jacobian = Eigen::Matrix<double, 3, 3>::Zero();
// 对位置的雅可比(只有高度约束与位置有关)
jacobian.block<2, 3>(0, 0).setZero(); // 方向约束与位置无关
jacobian.block<1, 3>(2, 0) = e3.transpose() * pi_R_G;
jacobian_pos = sqrt_information_ * jacobian;
}
// 对四元数的雅可比计算
if (jacobians[1]) {
Eigen::Map<Eigen::Matrix<double, 3, 4>, Eigen::RowMajor> jacobian_quat(jacobians[1]);
// 计算残差对四元数的雅可比
// 首先计算残差对旋转矩阵的导数
Eigen::Matrix<double, 3, 3> dres_dR = Eigen::Matrix<double, 3, 3>::Zero();
// 前两个残差对旋转的导数
dres_dR.block<2, 3>(0, 0) = -Lambda * pi_R_G * skew(G_R_O * e3);
// 第三个残差与旋转无关
dres_dR.block<1, 3>(2, 0).setZero();
// 然后计算旋转矩阵对四元数的导数 (3x4)
// 四元数 q = [w, x, y, z],旋转矩阵 R(q)
Eigen::Quaterniond q = q_a;
Eigen::Matrix<double, 3, 4> dR_dq = Eigen::Matrix<double, 3, 4>::Zero();
// 旋转矩阵对四元数的导数公式
// dR/dq = [dR/dw, dR/dx, dR/dy, dR/dz]
double w = q.w(), x = q.x(), y = q.y(), z = q.z();
// 对 w 的导数(第0列)
// ∂R/∂w = 2 * [0, -z, y; z, 0, -x; -y, x, 0]
dR_dq(0, 0) = 0; dR_dq(0, 1) = -2*z; dR_dq(0, 2) = 2*y;
dR_dq(1, 0) = 2*z; dR_dq(1, 1) = 0; dR_dq(1, 2) = -2*x;
dR_dq(2, 0) = -2*y; dR_dq(2, 1) = 2*x; dR_dq(2, 2) = 0;
// 对 x 的导数(第1列)
// ∂R/∂x = 2 * [0, y, z; y, -2x, -w; z, w, -2x]
dR_dq(0, 3) = 0; dR_dq(0, 4) = 2*y; dR_dq(0, 5) = 2*z;
dR_dq(1, 3) = 2*y; dR_dq(1, 4) = -4*x; dR_dq(1, 5) = -2*w;
dR_dq(2, 3) = 2*z; dR_dq(2, 4) = 2*w; dR_dq(2, 5) = -4*x;
// 对 y 的导数(第2列)
// ∂R/∂y = 2 * [-2y, x, -w; x, 0, z; -w, z, -2y]
dR_dq(0, 6) = -4*y; dR_dq(0, 7) = 2*x; dR_dq(0, 8) = -2*w;
dR_dq(1, 6) = 2*x; dR_dq(1, 7) = 0; dR_dq(1, 8) = 2*z;
dR_dq(2, 6) = -2*w; dR_dq(2, 7) = 2*z; dR_dq(2, 8) = -4*y;
// 对 z 的导数(第3列)
// ∂R/∂z = 2 * [-2z, -w, x; w, -2z, y; x, y, 0]
dR_dq(0, 9) = -4*z; dR_dq(0, 10) = -2*w; dR_dq(0, 11) = 2*x;
dR_dq(1, 9) = 2*w; dR_dq(1, 10) = -4*z; dR_dq(1, 11) = 2*y;
dR_dq(2, 9) = 2*x; dR_dq(2, 10) = 2*y; dR_dq(2, 11) = 0;
// 链式法则:dres/dq = dres/dR * dR/dq
Eigen::Matrix<double, 3, 4> dres_dq = dres_dR * dR_dq;
// 应用信息矩阵
jacobian_quat = sqrt_information_ * dres_dq;
}
return true;
}注意上述残差与之前基本无区别,雅克比部分与之前章节也区别不大,唯一区别较大的地方是,对四元素求雅克比,这里展开下

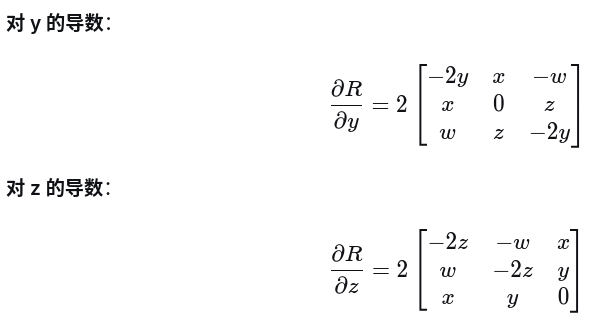
也可以

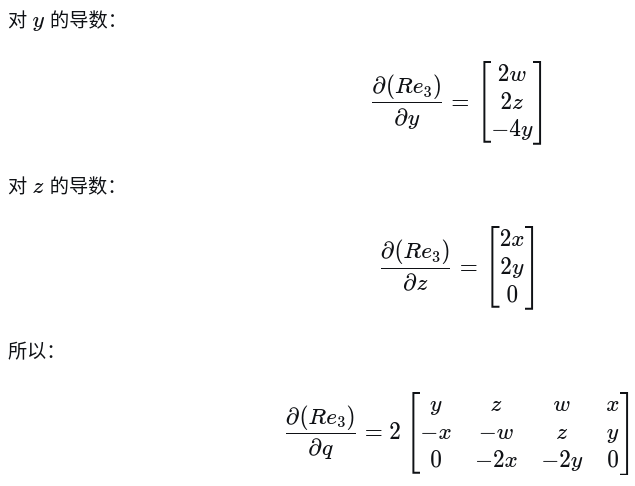
上述公式唯一要注意的点是旋转矩阵的表示形式
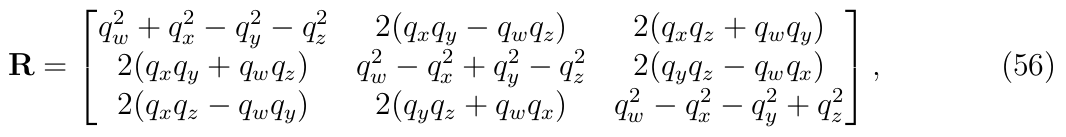
式(56)实际上是哈密顿约定(Hamilton Convention): 四元数表示为:q = [w, x, y, z] ,其中 w 是实部;
本文用的是JPL约定(Shuster Convention): 四元数表示为:q = [x, y, z, w] ,其中 w 是实部但放在最后
两种形式完全是等价的,可以利用单位四元数的模长是1,将两个的旋转矩阵的每个元素来一一转换
效果展示

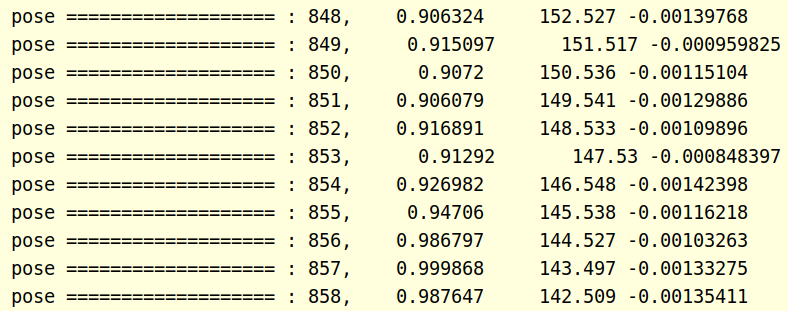
总结
本节利用ceres-solver解析解进行平面约束求解,实际结果证明,再z轴方向确实能将结果拉成接近于0,也证明算法的有效性