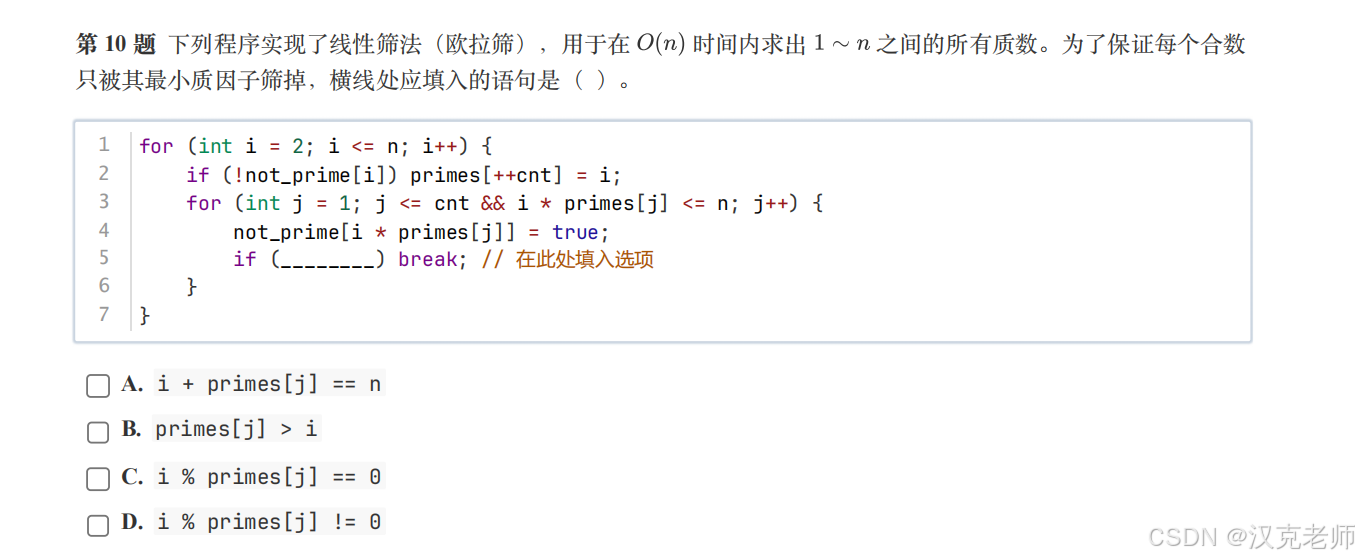
🧩 第 10 题:质数工厂的"线性筛魔法"
1、📖 故事背景
(1)在 数字王国 🏰 里,有一家 质数工厂:
国王想要知道:
👉 1~n 之间,哪些是质数?
(2)老方法太慢,于是请来了
🧙♂️ **欧拉大师(Euler),**发明了一种超快方法:
✨ 线性筛(欧拉筛)
2、🧠 线性筛在干什么?
📌 保证每个合数,只被"它最小的质因子"筛掉一次
这样,程序才会跑得非常快 🚀
3、🧠 代码回顾(关键位置)
cpp
for (int i = 2; i <= n; i++) {
if (!not_prime[i]) primes[++cnt] = i;
for (int j = 1; j <= cnt && i * primes[j] <= n; j++) {
not_prime[i * primes[j]] = true;
if (________) break;
}
}4、🧠 横线这里到底在干嘛?
这是线性筛最最关键的一句!
5、🧠 正确逻辑
(1) 假设:
-
当前数字是
i -
正在用质数
primes[j]去筛
🛑 一旦发现:
cpp
i % primes[j] == 0(2) 说明:
-
primes[j]已经是i的 最小质因子 -
再往后的质数,
👉 不可能是最小的了
-
必须立刻停!
(3) ✅ 正确填空
cpp
if (i % primes[j] == 0) break;6、✅ 正确答案
👉 C
7、🌟 记忆口诀
✔️ 线性筛,真线性,"每个数只处理一次"
✔️ 当前数字 叫 小 i ,
✔️ 小 i 的最小因数已出现,小 i 马上就走开
✔️ if (i % primes[j] == 0) break;

🧩 第 11 题:类的"出生与告别"(构造 & 析构)
1、📖 故事背景
在 类王国 👑 里:
-
每创建一个对象
👉 就像一个小宝宝出生 👶
-
每销毁一个对象
👉 就像一个人离开 👋
2、🧠 题目问什么?
👉 下面哪一句话是正确的?
🧩 四个选项逐个看
❌ A:派生类可以访问基类 private 成员
🚫 错!
-
private:👉 只有自己能用
-
子类也不行!
❌ B:private 继承后,protected 变 public
🚫 完全错误!
-
private 继承后:
👉 public / protected
👉 都会变成 private
❌ D:销毁时先析构基类
🚫 顺序反了!
3、✅ C:正确说法
创建派生类对象时:
先调用基类构造函数,
再调用派生类构造函数
4、🧠 C++ 与"类"相关的两个重要函数
| 名字 | 作用 |
|---|---|
| 构造函数 | 对象出生时调用 |
| 析构函数 | 对象消失时调用 |
5、🧠 用故事记住顺序
(1)🏠 盖房子顺序:
1️⃣ 先打地基(基类)
2️⃣ 再盖楼层(派生类)
(2)🧨 拆房子顺序:
1️⃣ 先拆楼层(派生类)
2️⃣ 再拆地基(基类)


🧩 第 12 题:函数里的"隐藏数学规律"
1、📖 故事背景
小明在写一个程序,
他输入了一个数字 n = 6,
程序是这样的:
cpp
#include <iostream>
using namespace std;
int f(int n) {
if (n <= 3) return n;
return f(n - 1) + f(n - 2) + 2 * f(n - 3);
}
int main() {
int n;
cin >> n;
cout << f(n) << endl;
return 0;
}问:
👀 程序最后输出多少?
2、🧠 别慌!一步一步来
🧠 我们来手算(要仔细)
(1) n = 1 👉 f(1) = 1
(2) n = 2 👉 f(2) = 1
(3) n = 3 👉 f(3) = 3
(4) n = 4 👉 f(4) = f(4 - 1) + f(4 - 2) + 2 * f(4 - 3);
👉 f(4) = f(3) + f(2) + 2 * f(1) = 3 + 2 + 2 * 1 = 7
(5) n = 5 👉 f(5) = f(5 - 1) + f(5 - 2) + 2 * f(5 - 3);
👉 f(5) = f(4) + f(3) + 2 * f(2) = 7 + 3 + 2 * 2 = 14
(6) n = 6 👉 f(6) = f(6 - 1) + f(6 - 2) + 2 * f(6 - 3);
👉 f(6) = f(5) + f(4) + 2 * f(3) = 14+ 7 + 3 * 2 = 27
3、✅ 正确答案
👉 B. 27
4、🌟 记忆口诀
✔️ 见递归,莫惊慌
✔️ 找到起点,才开始
✔️ 递归来把递推转
✔️ 一步一步到终点