Counting Towers

洛生&2026-01-10 18:40

题目描述

Your task is to build a tower whose width is 2 and height is n. You have an unlimited supply of blocks whose width and height are integers.

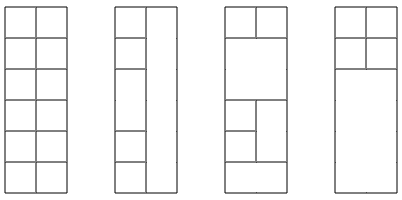
For example, here are some possible solutions for n=6:

Given n, how many different towers can you build? Mirrored and rotated towers are counted separately if they look different.

输入

The first input line contains an integer t: the number of tests.

After this, there are t lines, and each line contains an integer n: the height of the tower.

Constraints

1 ≤ t ≤ 100

1 ≤ n ≤

输出

For each test, print the number of towers modulo

样例输入
复制代码
3
2
6
1337
样例输出
复制代码
8
2864
640403945

题目大意： 建立一个宽为2，高为n的塔，有无限的宽度高度都为整数的方块，问最终可以构建出多少种塔，最终的方法数要模

**方法：**很明显的dp题，关键就是状态转移方程怎么想，由于塔的宽度仅为2，所以我们分析塔的一行，可以发现有两种情况，一个是塔的一行是同一个方块，一个则是来自不同方块，我们分别将这两种类型记作a和b，最终的方法数就是an+bn，接下来分析an和bn的计算：

an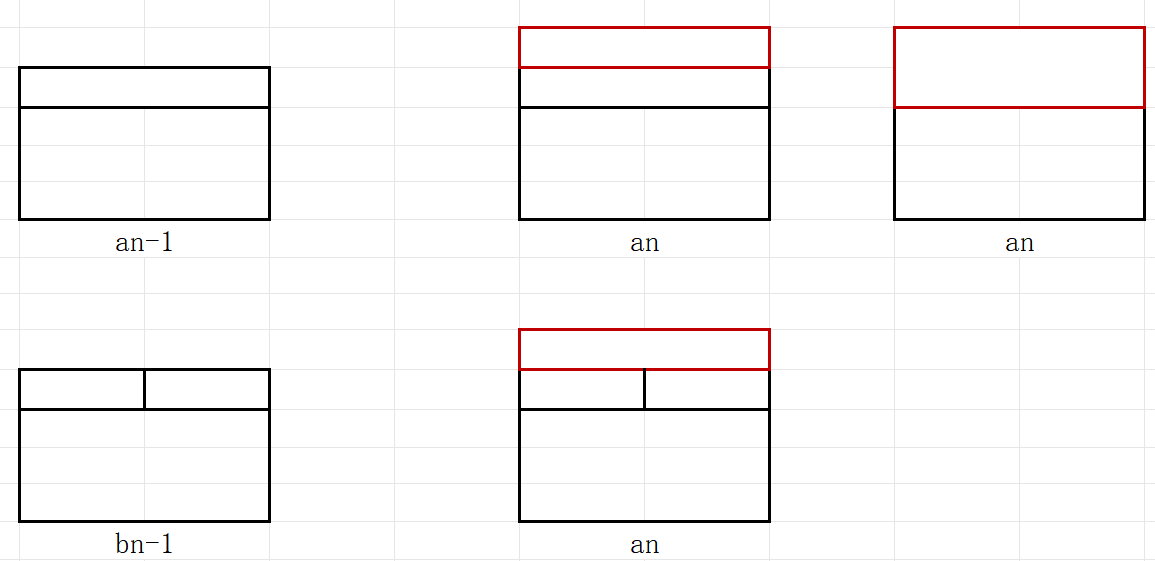：an=2*an-1+bn-1

bn:

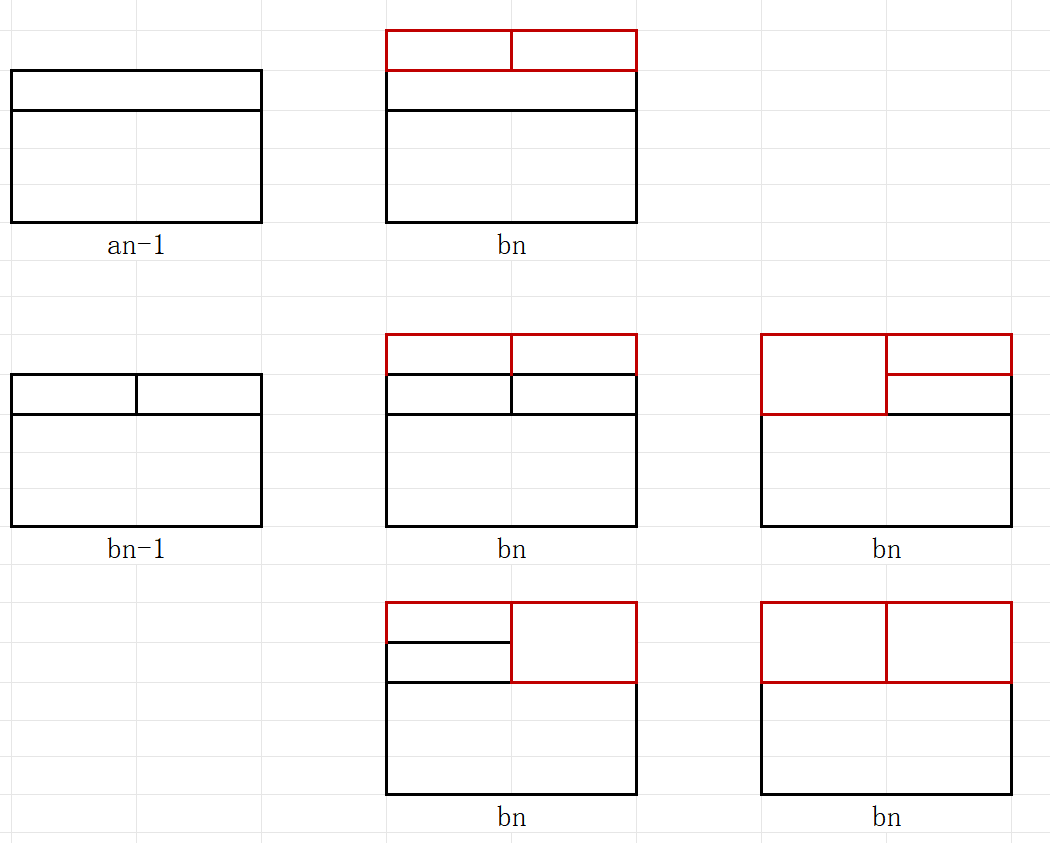
bn=an-1+4*bn-1

代码

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int mod=1000000007;
const int N=1000000;
ll a[N+10],b[N+10];
int main(){
    int t;cin>>t;
    a[1]=1,b[1]=1;
    for (int i=2;i<=N;i++){
        a[i]=(2*a[i-1]+b[i-1])%mod;
        b[i]=(a[i-1]+4*b[i-1])%mod;
    }
    while(t--){
        int n;cin>>n;
        cout<<(a[n]+b[n])%mod<<"\n";
    }
    return 0;
}