更弱智的算法学习 day25

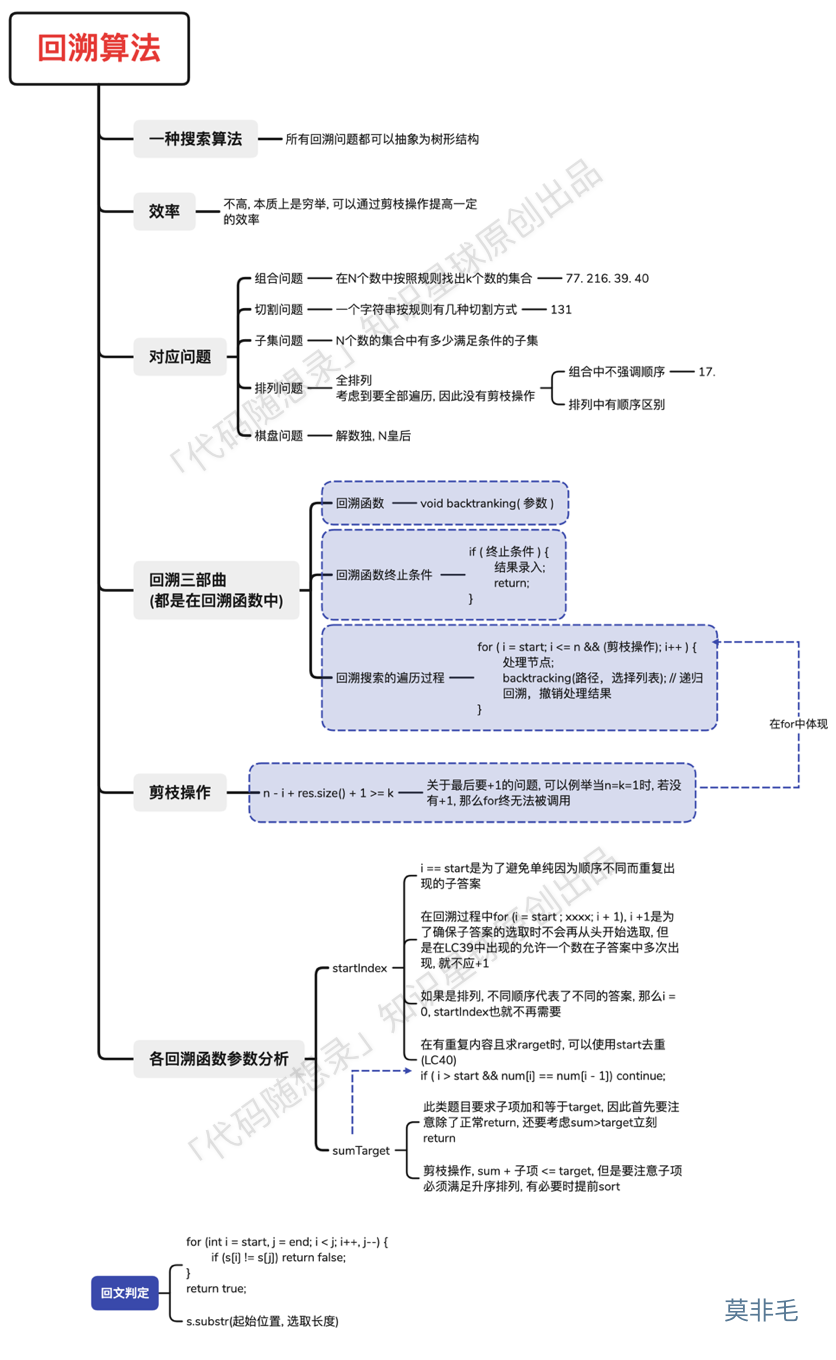
491.递增子序列

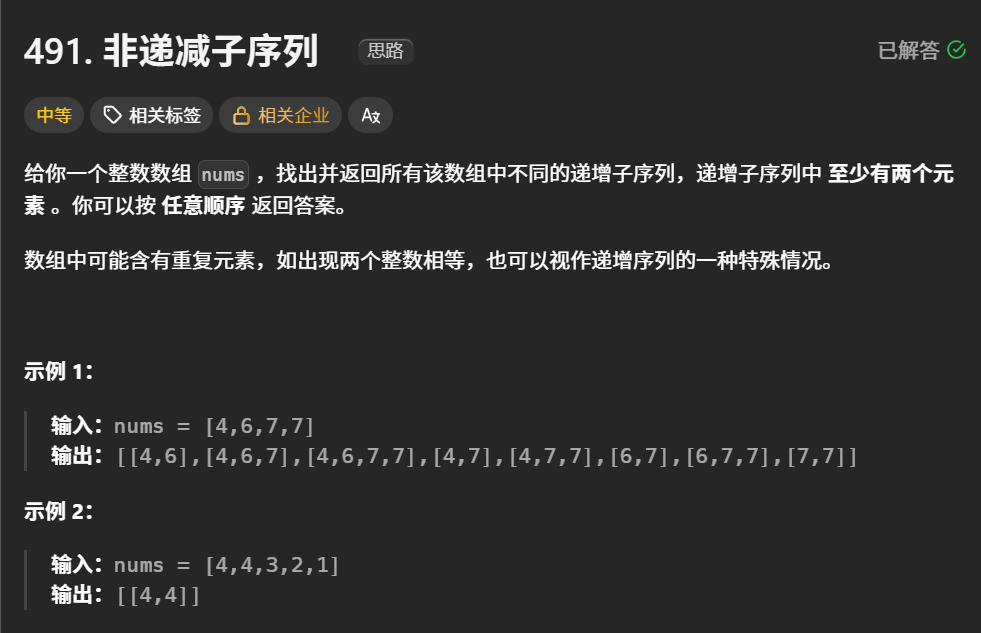
简单整理一下逻辑：本题和昨天的看上去像，实际上不太相同：

首先要考虑因为重复问题引起的去重需求，对于4676数组而言，会出现不同的两个46，而该数组不能排序，所以无法用之前的逻辑进行去重，我们新的去重逻辑应该是，在本层树中使用过该数字了，如6，就不再使用了，因此给定一个set集合，每使用一个数，就装入集合中，后续使用的时候，检查是否在集合中已经出现过了。

加入out数组的逻辑是，在out存在时，检查其最后一位和当前i位置数组大小

python 复制代码

class Solution:
    def findSubsequences(self, nums: List[int]) -> List[List[int]]:
        self.out = []
        self.res = []
        self.backtrack(nums, 0)
        return self.res

    def backtrack(self, nums, start):
        if len(self.out) >= 2:
            self.res.append(list(self.out))
            # return  这里不返回，而是继续寻找更长的子序列
        used = set()

        for i in range(start, len(nums)):
            if self.out and nums[i] < self.out[-1]:
                continue
            if nums[i] in used:
                continue
            used.add(nums[i])
            self.out.append(nums[i])
            self.backtrack(nums,i+1)
            self.out.pop()

46.全排列

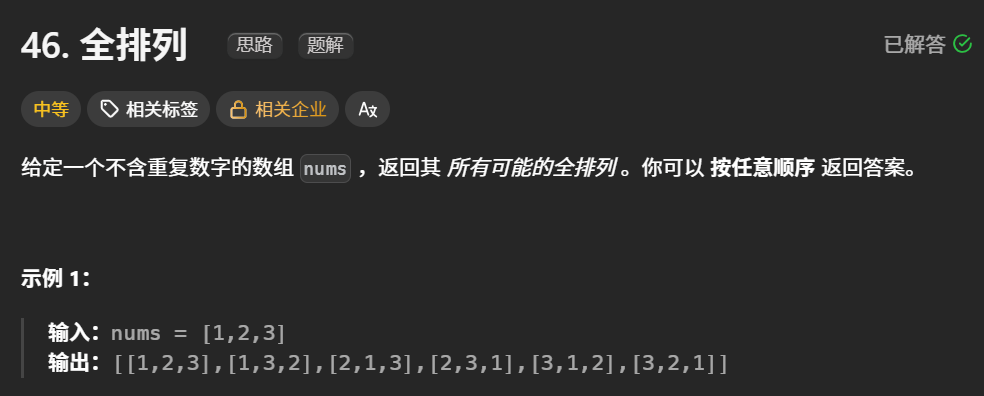
这个题前面已经做过，但是依然做错，嘻嘻。

全排列和组合的区别是顺序，也即132和123都是一个组合，但是不是一个排列，因此只要保证每一子树下面不适用相同元素即可，这里用used数组标注了使用过的元素

python 复制代码

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        self.out = []
        self.res = []
        self.used = [False] * len(nums)
        self.backtrack(nums)
        return self.res

    def backtrack(self,nums):
        if len(self.out) == len(nums):
            self.res.append(list(self.out))
            return

        for i in range(len(nums)):
            if self.used[i] is True:
                continue
            self.out.append(nums[i])
            self.used[i] = True 
            self.backtrack(nums)
            self.out.pop()
            self.used[i] = False

47.全排列 II

由于包含了可重复数，因此多了一个去重的逻辑，和之前使用的相似

if self.used[i-1] and nums[i-1] == nums[i] and i>0:

其他地方的内容相似

python 复制代码

class Solution:
    def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        self.out = []
        self.res = []
        self.used = [False] * len(nums)
        nums.sort()
        self.backtrack(nums)
        return self.res


    def backtrack(self, nums):
        if len(self.out) == len(nums):
            self.res.append(list(self.out))
            return

        for i in range(len(nums)):
            if self.used[i-1] and nums[i-1] == nums[i] and i>0:
                continue
            if self.used[i]:
                continue
            self.out.append(nums[i])
            self.used[i] = True
            self.backtrack(nums)
            self.out.pop()
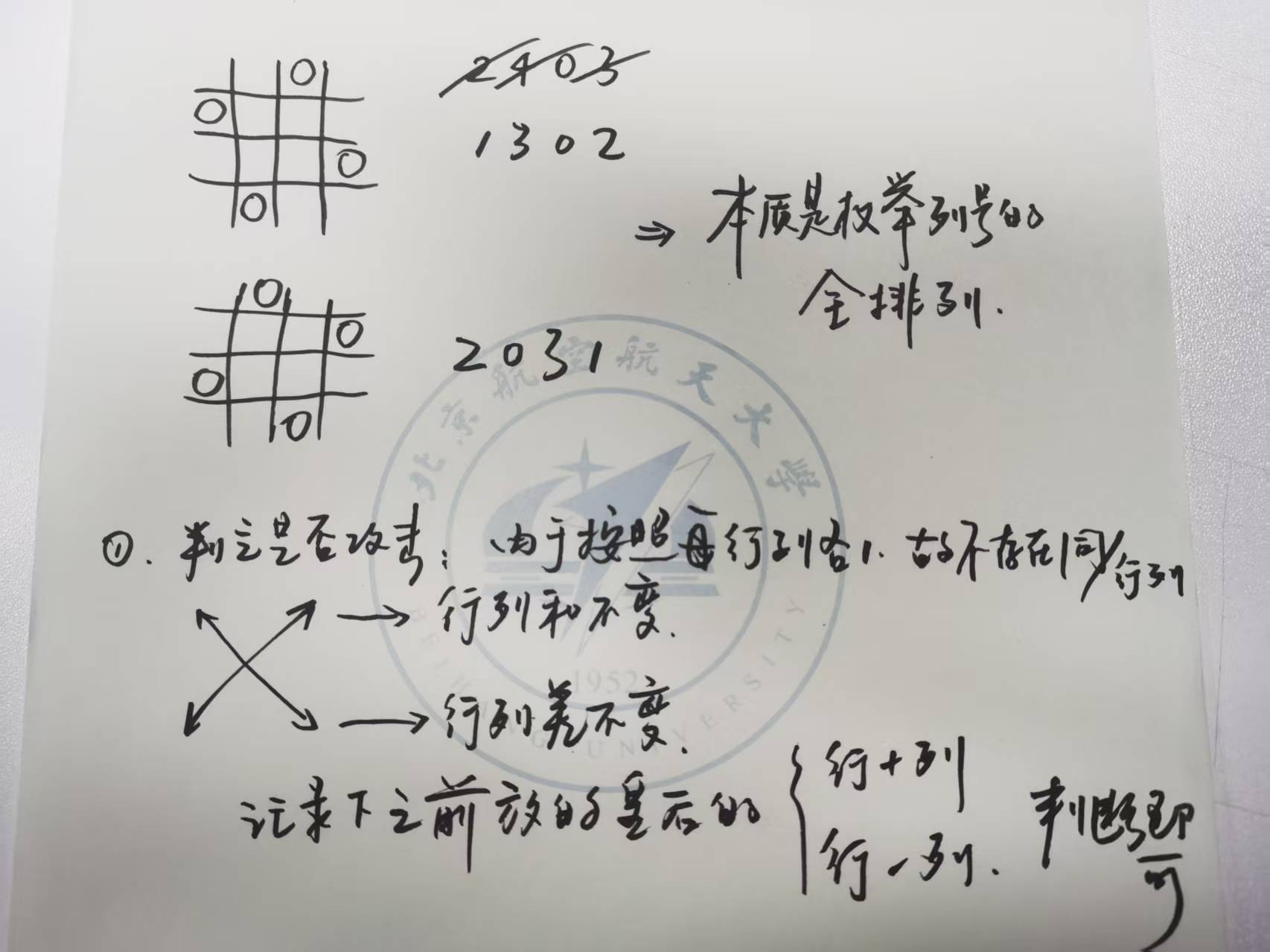
            self.used[i] = False

N皇后（适当跳过）

巧妙啊。

这个题目小时候抱过我，印象真是很深刻。

下面这个思路用上，我们逐行处理位置即可

python 复制代码

class Solution:
    def solveNQueens(self, n: int) -> List[List[str]]:
        self.out = []
        self.res = []
        self.sumqueen = []
        self.diffqueen = []
        self.used = [False]*n


        self.backtrack(n,0) #从0行开始
        return self.res

    def backtrack(self,n,row):
        if len(self.out) == n:
            chessboard = []
            for i in self.out:
                row = '.'*i + 'Q'+'.'*(n-1-i)
                chessboard.append(row)
            self.res.append(chessboard)
            return

        for i in range(n):
            if self.used[i] is True:
                continue
            if row+i in self.sumqueen or row-i in self.diffqueen:
                continue
            self.out.append(i)
            self.used[i] = True
            self.sumqueen.append(row+i)
            self.diffqueen.append(row-i)
            self.backtrack(n,row+1)
            self.out.pop()
            self.used[i] = False
            self.sumqueen.pop()
            self.diffqueen.pop()

解数独（适当跳过）

这有点复杂了，我看不如跳过

更弱智的算法学习 day25

491.递增子序列

46.全排列

47.全排列 II

总结