想象你是班主任,拿到了班上25名学生的数学考试成绩(满分100),分数如下:
45, 52, 59, 61, 62, 63, 65, 66, 68, 70, 72, 74, 75, 75, 76, 77, 78, 81, 82, 85, 88, 90, 92, 95, 98
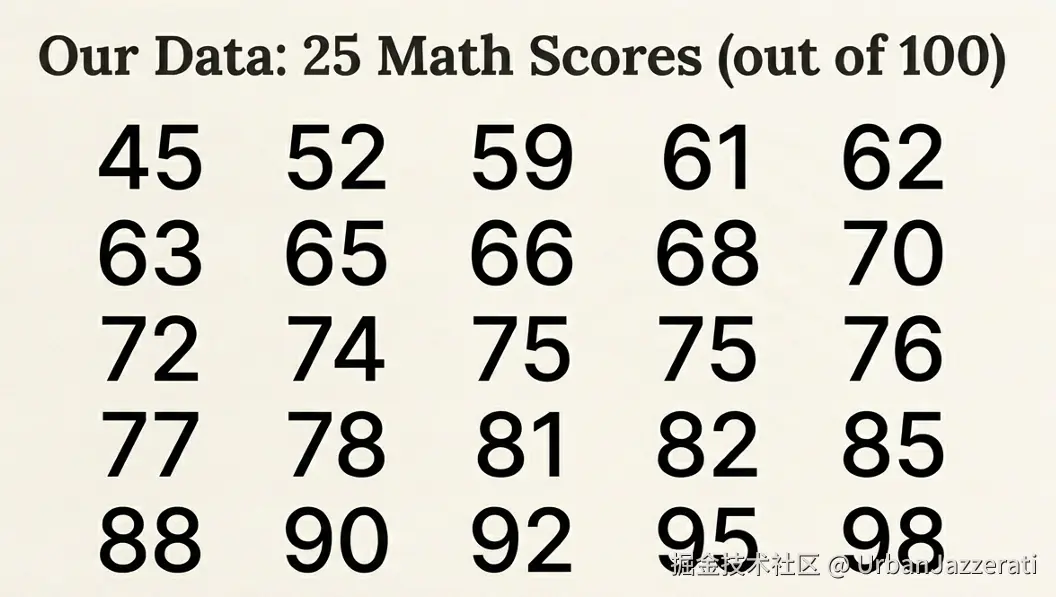
让我们看看茎叶图和箱线图分别怎么"描绘"这群学生的成绩。
第一部分:茎叶图 --- 像一株植物,列出所有细节
一、它是什么?
茎叶图是一种将原始数据 和数据分布形状结合显示的图表。它像一株植物,"茎"是高位数字,"叶"是低位数字,所有数据点一目了然。
二、怎么画?(用我们的成绩数据)
-
分茎和叶:这里我们取十位数作"茎",个位数作"叶"。
-
画竖线:在纸上画一条竖线。
-
写"茎" :在竖线左侧,从最小十位数到最大十位数,依次写下:4, 5, 6, 7, 8, 9。
-
添"叶" :遍历每个分数,将它的个位数(叶),按顺序写在对应茎的右侧。
- 第一个分数45 → 茎是
4,叶是5,在4的右边记一个5。 - 第二个分数52 → 茎是
5,叶是2,在5的右边记一个2。 - 以此类推...
- 第一个分数45 → 茎是
最终得到的茎叶图如下:
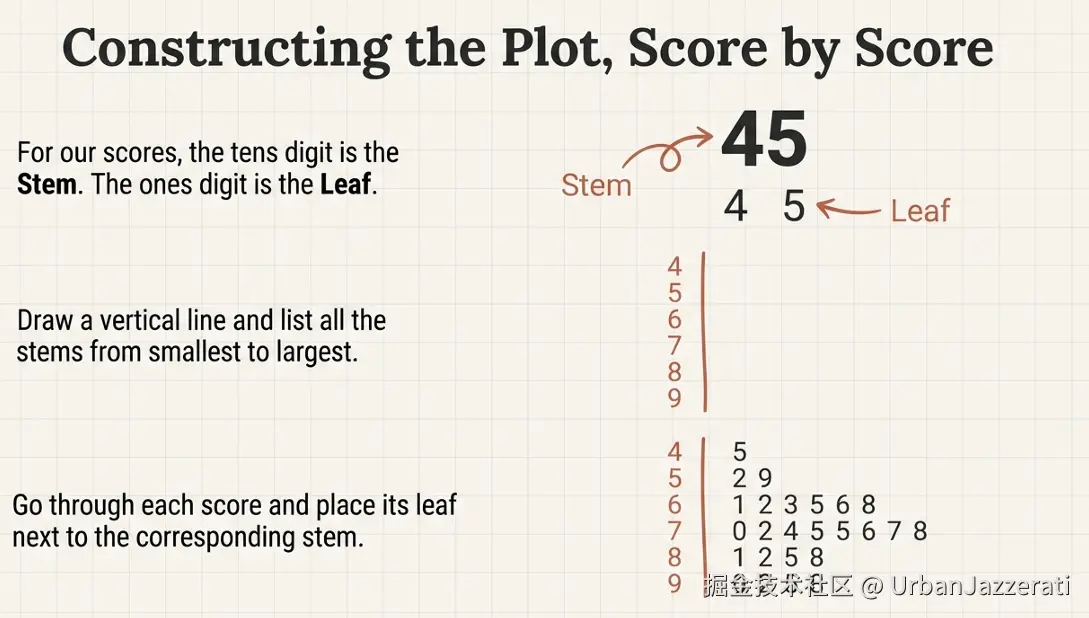
markdown
数学考试成绩茎叶图
十位(茎) | 个位(叶)
-----------------
4 | 5
5 | 2 9
6 | 1 2 3 5 6 8
7 | 0 2 4 5 5 6 7 8
8 | 1 2 5 8
9 | 0 2 5 8(注:为了清晰,我们已将"叶"从小到大排序)
三、它能告诉我们什么?(解读图例)
- 看整体形状:数据集中在60-80多分之间(茎6,7,8),形状大致对称,像一座小山。
- 找具体数据 :可以直接读出每个分数!比如
7 | 0 2 4 5 5 6 7 8表示有70, 72, 74, 75, 75, 76, 77, 78分的学生。这是它独一无二的优点。 - 发现异常值:最低分45分(茎4)看起来有点"离群"。
四、优点与局限
- 优点 :保留了每个原始数据,直观展示分布,制作简单。
- 局限:数据量很大(比如几百个)时,会变得冗长、混乱,不适合用。
第二部分:箱线图 --- 五个数字,概括全局
如果说茎叶图是"工笔画",列出所有细节,那么箱线图就是"简笔画",用五个关键数字 概括数据的整体分布。 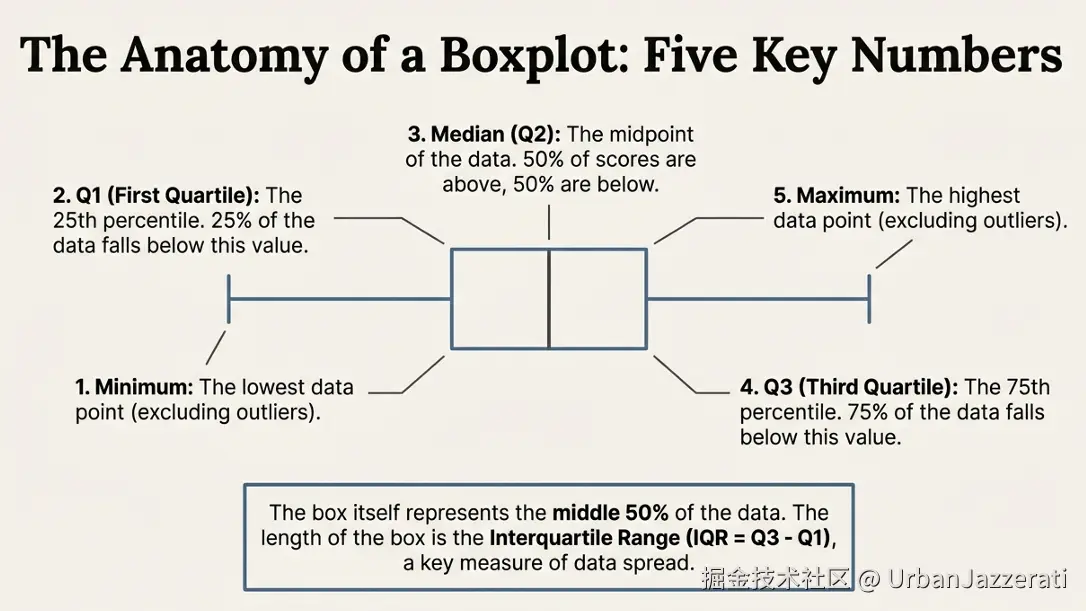 一、五个关键数字是什么?
一、五个关键数字是什么?
让我们先计算成绩数据的这五个数:
- 最小值 :
45(非异常值的最小值) - 第一四分位数 :
66(将所有数据从小到大排序,位于前25%位置的数,记作Q1) - 中位数 :
75(排序后正中间的数,记作Q2或中位数) - 第三四分位数 :
82(位于前75%位置的数,记作Q3) - 最大值 :
98(非异常值的最大值)

二、箱线图长什么样?(基于以上五个数) 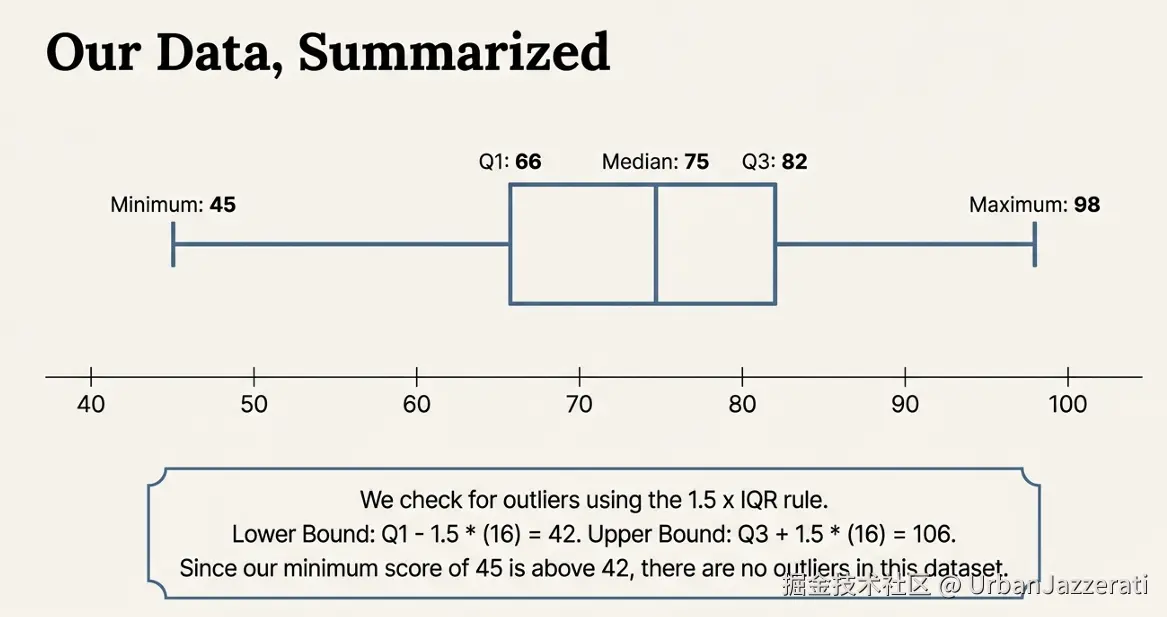
scss
最小值 Q1 中位数 Q3 最大值
|-----[====|====]-----|
45 66 75 82 98
↓ ↓ ↓ ↓
下界 箱子起点 箱子终点 上界
(IQR范围)([ ]表示箱子,|在箱子中间是中位数,-----是须线)
更标准的箱线图还会标出可能的异常值(用点·表示) 。
三、它能告诉我们什么?(解读图例)
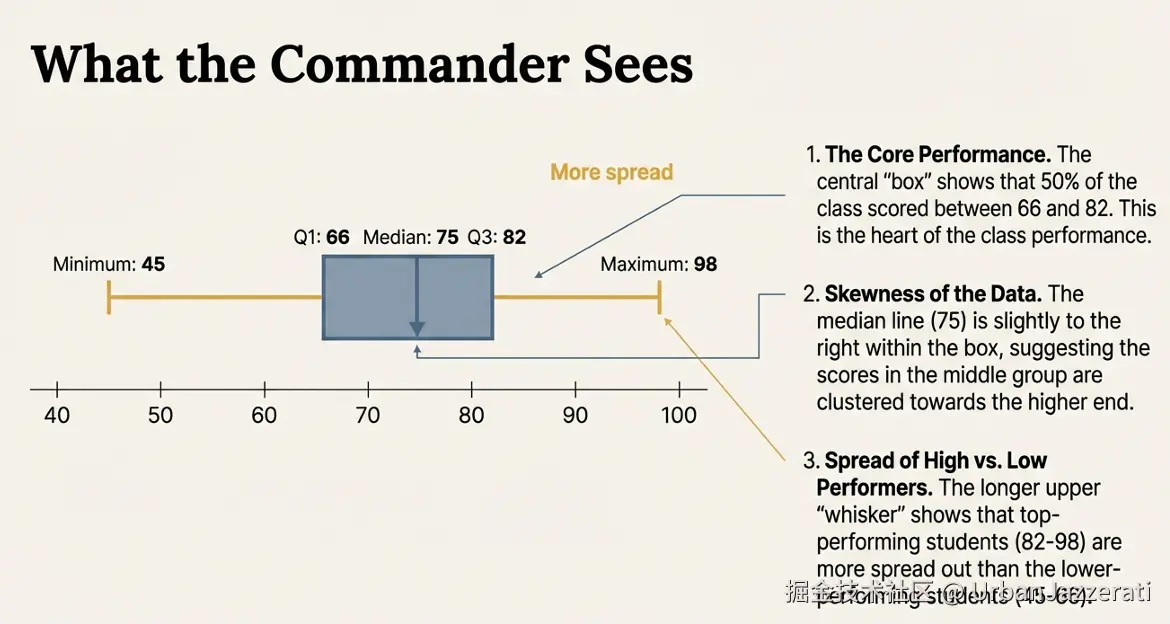
-
看箱子的位置和长度:
- 箱子包含了中间50%的数据(从Q1到Q3,即66分到82分)。
- 箱子长度 = Q3 - Q1 = 16,这叫四分位距,反映了中间半数数据的波动范围。这里箱子不长,说明中等水平的学生成绩比较集中。
- 中位数线(75) 在箱子中间偏右一点,说明成绩分布稍微偏向高分一侧。
-
看须线的长度:
- 下须线(Q1到最小值45)比上须线(Q3到最大值98)长很多,说明高=低分学生分布更分散,而高分学生(除了个别)相对集中。
-
识别异常值:
-
箱线图通常用
1.5倍IQR规则判断异常值。本例中:- 下界 = Q1 - 1.5*IQR = 66 - 24 = 42
- 上界 = Q3 + 1.5*IQR = 82 + 24 = 106
-
分数
45高于下界42,所以没有异常值 。如果有分数低于42,就会被单独标为异常点·。
-
四、箱线图的巨大威力:多组比较
这是箱线图最不可替代的用途!一眼比较不同班级、不同方法的效果。
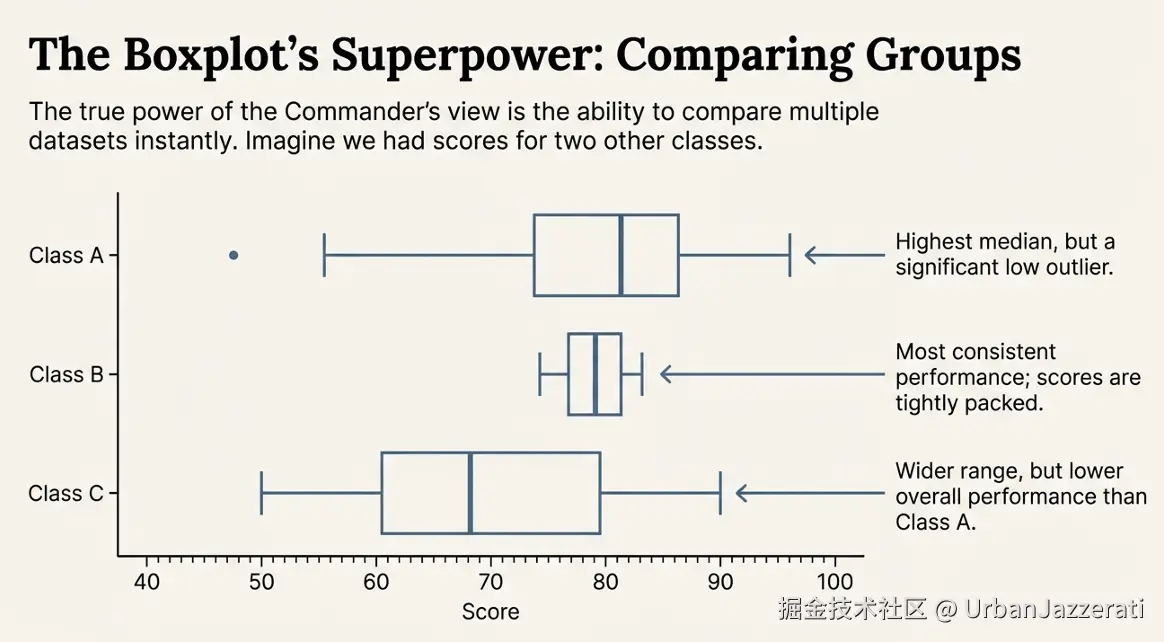
css
班级A成绩 |---[==|==]---|·········>
班级B成绩 |---[=|==]---|
班级C成绩 |---[===|===]---|
←---------------分数---------------→一眼看出:A班中位数最高,但有个超低异常值;B班整体紧凑;C班整体偏低但均匀。
第三部分:总结与对比
| 特性 | 茎叶图 | 箱线图 |
|---|---|---|
| 核心功能 | 展示细节,列出每个数据点 | 概括分布,用五个统计量总结 |
| 呈现信息 | 所有原始数据、分布形状 | 中位数、四分位范围、极值、异常值 |
| 最佳场景 | 数据量小(如<50),需要精确知道每个值时 | 数据量大,快速了解分布概况,特别适合多组数据对比 |
| 优点 | 不丢失原始信息,制作简单 | 简洁有力,对异常值敏感,比较能力强 |
| 局限 | 数据量大时混乱不堪 | 丢失了数据分布的细节(如双峰分布) |
给你的最终指南
- 如果你是"考古学家" ,想仔细审视一小批数据的每一个细节,用茎叶图。
- 如果你是"指挥官" ,想快速把握一批或多批数据的整体分布、典型水平和异常情况,用箱线图。
记住这个口诀:
茎叶图,个个现,数据一多就花眼。
箱线图,五条线,分布异常全看见。