数学建模美赛倒计时，选对适合自己团队的题目将会事半功倍，本文将分析美赛ABCDEF题目特点，并总结数学建模常用模型及算法。
一、美赛题目浅析
美国大学生数学建模竞赛（MCM/ICM）是由美国数学及其应用联合会（COMAP）组织的一项国际性赛事。该竞赛要求参赛队伍由三名本科生组成，在四天的时间内，针对给定问题完成数学模型构建、求解、验证以及英文论文撰写等全部工作。
- **竞赛时间（北京时间）：**2026年1月30日 06：00~2026年2月3日 09：00
- **论文提交截止：**2026年2月3日10:00
- **竞赛结果：**预计2026年5月8日
1、题型设置
（1 ）两大类型
美赛题目主要分为两种类型：MCM 与ICM
- MCM（Mathematical Contest in Modeling，数学建模竞赛）通常对应A、B、C三道题，侧重传统数学建模方法，要求参赛者运用数学工具分析与解决特定问题。
- ICM（Interdisciplinary Contest in Modeling，跨学科建模竞赛）则对应D、E、F题，内容更具交叉学科特色，常涉及社会经济、环境政策、网络科学等领域，需要综合多学科知识进行建模。
（2 ）六个题目
- A **题连续型问题：**变量连续变化，常涉及微分方程、物理建模，如2025年"楼梯磨损分析"。专业和编程要求高。类、决策树分类、支持向量机分类等。
- B **题离散型问题：**变量离散变化，常涉及图论、组合优化、离散算法。同样对建模和编程能力要求较高。
- C **题大数据问题：**官方常会提供数据集，侧重数据分析、机器学习、时间序列预测。需熟练掌握数据处理和编程。
- D **题运筹学问题：**核心是图论与优化问题，如资源分配、交通网络。对算法和数据结构基础要求高。
- E **题可持续性问题：**侧重环境、生态、资源可持续，如气候变化、生态系统模拟。题目较开放，对编程要求相对较低。
- F **题政策研究问题：**聚焦社会科学政策评估与制定，如教育、网络安全政策。非常开放，注重逻辑论证与写作。
2、选题建议
（1 ）建模与编程功底扎实------A/B/D 题
A、B、D 题整体对数学建模能力和编程基础要求较高，尤其是 D 题往往涉及图论与优化问题，若缺乏算法和数据结构基础，完成难度较大，因此参赛队伍相对较少，但竞争压力也相应较低；对于具备一定专业功底和编程能力的团队而言，只要模型思路清晰并能运行出结果，辅以适度创新，反而更具获奖优势。
（2 ）具备数据分析基础------C 题
相比之下，C、E、F 题上手门槛较低，更适合基础一般或首次参赛的队伍，其中 C 题因自带数据、分析路径清晰，参赛人数最多，但竞争也最为激烈，想要获得较高奖项往往需要在模型深度和创新性上进一步"内卷"。
（3 ）擅长逻辑与写作------E/F 题
E、F 题对编程依赖较小，常规模型即可完成问题，因此论文结构、图表呈现和整体表达质量在评分中占据更大比重。
综合来看，新手队伍更适合从 C、E、F 题入手；专业背景扎实、具备建模与编程能力的团队则可考虑 A、B、D 题。
3、数学建模常用模型
数学建模常用模型可分为评价模型、预测模型、分类与聚类模型、统计分析模型等。每类模型涉及方法有很多种，下图梳理了高频使用的模型算法，供大家查阅。
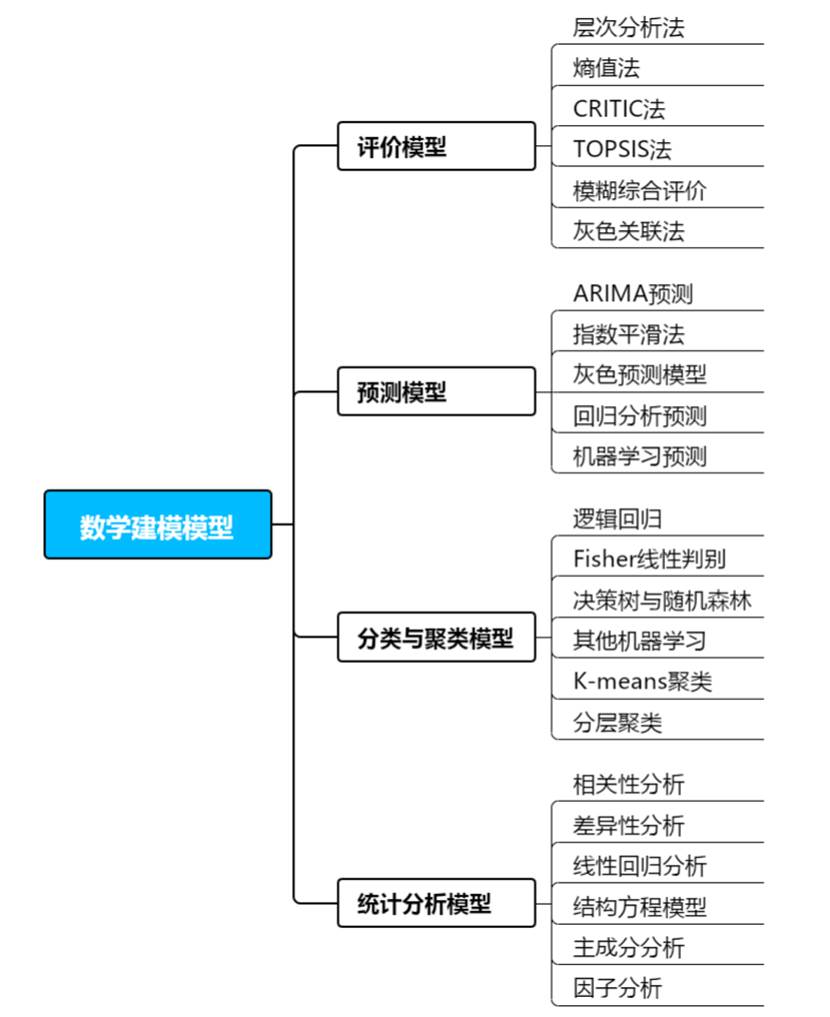
随着现代统计分析软件的快速发展，许多复杂模型已不再需要编程即可完成分析。例如，国产统计分析软件SPSSAU就能实现数学建模中绝大多数模型的分析，这对没有编程基础的同学来说非常友好。下面将详细介绍以上四大模型。
二、评价模型
评价模型主要用于对多个对象或方案进行综合评估和排序。常用方法包括权重计算与综合评价两大类。权重计算方法有AHP层次分析法、熵值法、CRITIC法等；综合评价方法有TOPSIS法、模糊综合评价、灰色关联法、Vikor法等。
1、层次分析法
AHP层次分析法是一种解决多目标复杂问题的定性和定量相结合进行计算决策权重的研究方法。通常包括三个步骤分别是：标度确定和构造判断矩阵；特征向量，特征根计算和权重计算；一致性检验分析。AHP层次分析法的数据格式比较特殊，需要手工录入判断矩阵，SPSSAU提供"和积法"与"方根法"计算，可自行选择，操作如下图：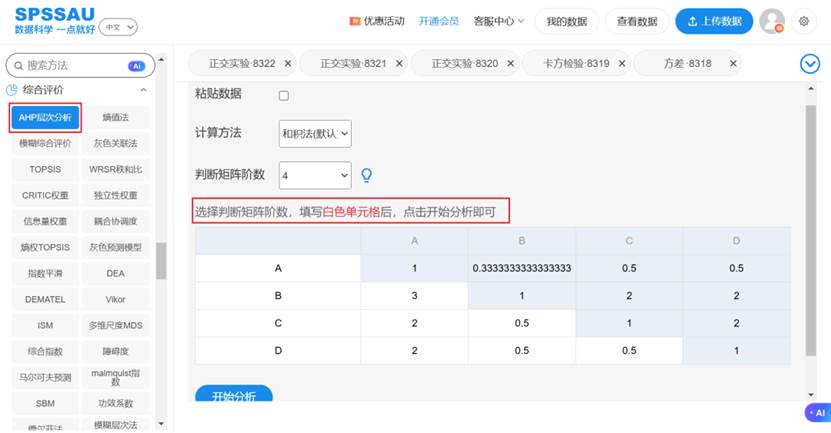
层次分析详细说明及案例操作解读可点击查看下方帮助手册：
2、熵值法
熵值是不确定性的一种度量。信息量越大，不确定性就越小，熵也就越小；信息量越小，不确定性越大，熵也越大。因而利用熵值携带的信息进行权重计算，结合各项指标的变异程度，利用信息熵这个工具，计算出各项指标的权重，为多指标综合评价提供依据。
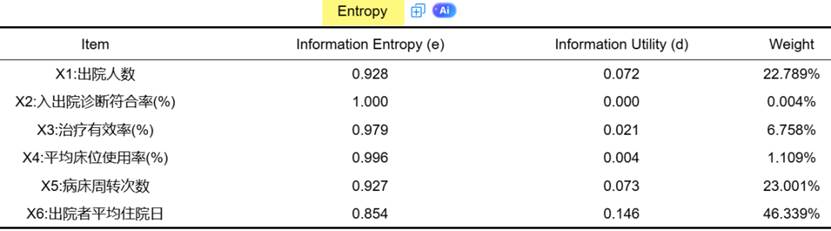
SPSSAU输出熵值法结果示例如下：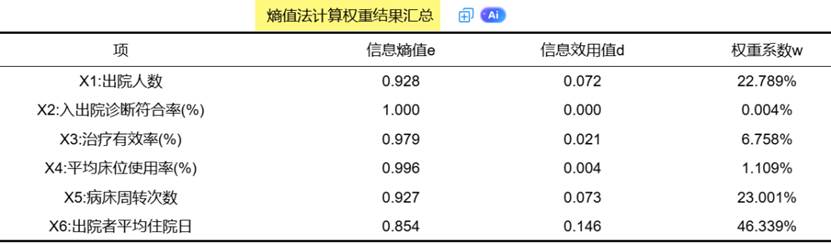
提示：SPSSAU输出分析结果为标准三线表格式 ，可直接复制到论文中使用，并可进行中英文切换，对美赛论文报告非常友好哦~
- SPSSAU中文版网址：https://spssau.com/
- SPSSAU国际版网址：https://spssau.net/
3、CRITIC法
CRITIC权重法是一种客观赋权法。其思想在于用于两项指标，分别是对比强度和冲突性指标。对比强度使用标准差进行表示，如果数据标准差越大说明波动越大，权重会越高；冲突性使用相关系数进行表示，如果指标之间的相关系数值越大，说明冲突性越小，那么其权重也就越低。权重计算时，对比强度与冲突性指标相乘，并且进行归一化处理，即得到最终的权重。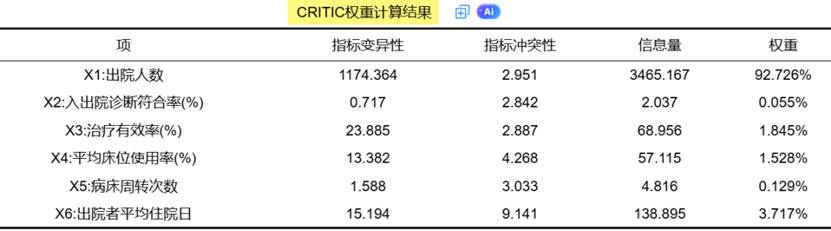
CRITIC法帮助手册
4、TOPSIS法
TOPSIS法是一种基于距离和相似性度量的多属性决策方法。TOPSIS法首先将多个备选方案与理想解进行比较，计算每个备选方案与理想解之间的相似性和距离。然后根据计算结果，评估和排序各个备选方案，选择最佳的方案。TOPSIS法能够较好地处理多属性决策问题，特别适用于需要考虑多个评价指标的情况。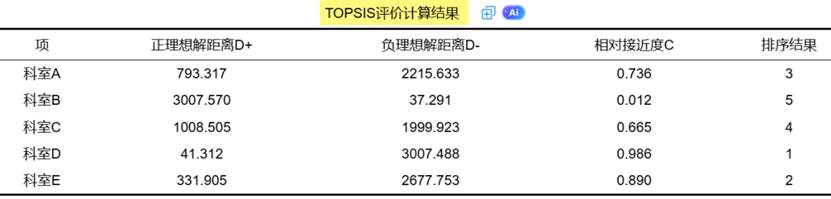
TOPSIS法帮助手册
5、模糊综合评价
模糊综合评价是一种处理具有模糊信息的评价方法。在模糊综合评价中，将模糊的评价指标通过隶属度函数转化为隶属度，然后根据权重给予不同指标不同的重要性。最后，通过对隶属度进行加权求和，得到一个综合评价结果。模糊综合评价方法能够有效处理不确定性和模糊性的问题，适用于现实世界中的复杂决策。
模糊综合评价帮助手册
6、灰色关联法
灰色关联分析法通过研究数据关联性大小（母序列与特征序列之间的关联程度），通过关联度（即关联性大小）进行度量数据之间的关联程度，从而辅助决策的一种研究方法。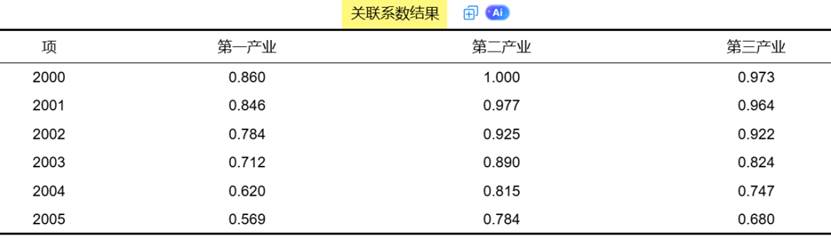
三、预测模型
预测模型是通过对历史数据的分析和建模，来预测未来趋势或结果的数学模型。常用的预测模型算法如ARIMA 预测、指数平滑法、灰色预测模型、回归分析预测、机器学习预测等。
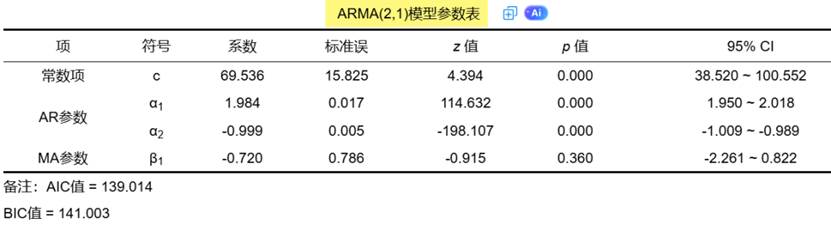
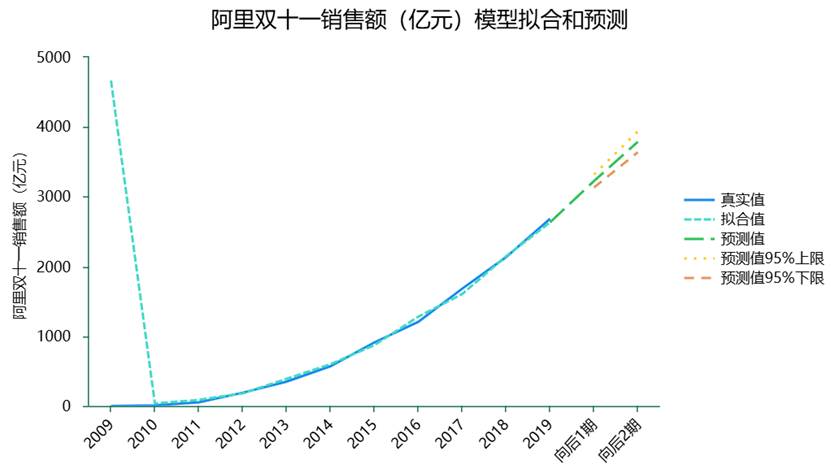
1、ARIMA预测
ARIMA模型是最常见的时间序列预测分析方法，适用于平稳时间序列数据**。** 它包括三个部分：自回归（AR）、差分（I）和移动平均（MA）。SPSSAU可以智能地找出最佳的AR模型，I即差分值和MA模型，并且最终给出最佳模型预测结果**。**当然，研究人员也可以自行设置参数进行模型构建。具体来说，ARIMA模型有以下三个参数：
- p：自回归阶数，表示当前观察值与前p个观察值之间的相关性。
- d：差分阶数，表示为使时间序列变得平稳所需的差分次数。如果平稳，则d=0。
- q：移动平均阶数，表示当前观察值与前q个观察值的残差之间的相关性。
2、指数平滑法
指数平滑法常用于数据序列较少时使用，且一般只适用于中短期预测。对于长期趋势或复杂非线性关系的数据可能表现不佳。一次平滑法为历史数据的加权预测，二次平滑法适用于具有一定线性趋势的数据，三次平滑法适用于具有一定曲线关系时使用。如果不设置平滑方法，SPSSAU将自动运行三种平滑方法，选择最优效果时对应的平滑方法。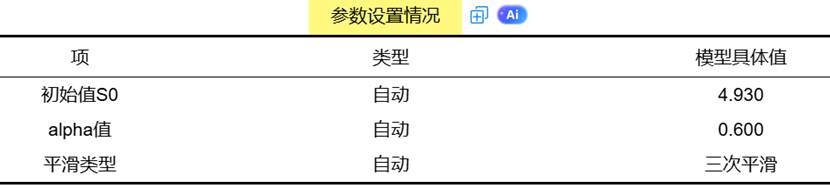
指数平滑法帮助手册
3、灰色预测模型
灰色预测模型可针对数量非常少（比如仅4个），数据完整性和可靠性较低的数据序列进行有效预测。其利用微分方程来充分挖掘数据的本质，建模所需信息少，精度较高，运算简便，易于检验，也不用考虑分布规律或变化趋势等。但灰色预测模型一般只适用于短期数据、有一定指数增长趋势的数据进行预测，不建议进行长期预测。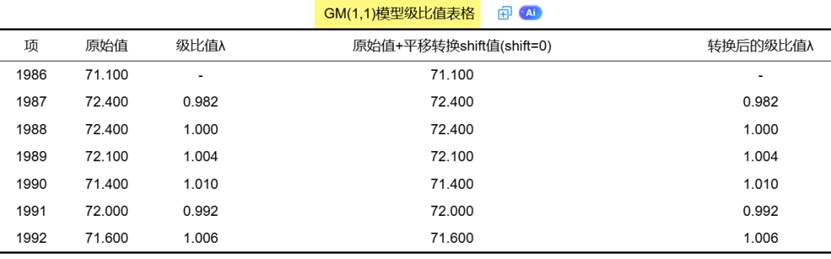
4、回归分析预测
回归分析是一种常用的统计方法，用于建立变量间的关系模型，并通过该模型对未知数据进行预测。常见的比如线性回归和logistic回归分析。
- **线性回归分析常用于预测数值型数据：**它基于自变量与因变量之间的线性关系建立模型，并利用该模型对未知的因变量进行预测。
- logistic **回归分析常用于预测分类变量数据：**可细分为三种------二元logistic回归、有序logistic回归和多分类logistic回归。
5、机器学习预测
机器学习是一种强大的技术，用于从数据中学习模式和规律，并利用这些知识进行预测。常用的预测类分析方法如决策树、随机森林、 K 近邻算法、朴素贝叶斯、支持向量机、神经网络等。 SPSSAU【机器学习】模块如下：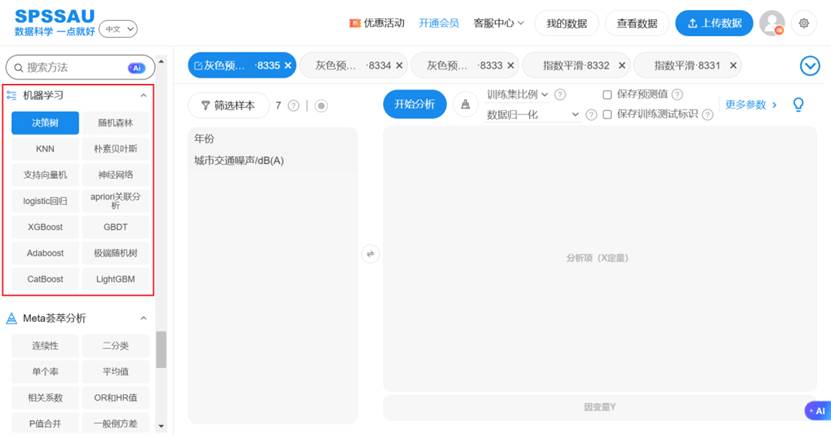
更多预测类分析方法查看下方文章：常用预测类数据分析方法分类汇总时间序列预测五类常用模型 | ARIMA、指数平滑、灰色预测、Sarima、VAR
四、分类与聚类模型
分类模型属于有监督学习，用于预测已知的类别标签（例如判断邮件是否为垃圾邮件），常用算法有逻辑回归、决策树、支持向量机等。而聚类模型属于无监督学习，用于探索数据内在的未知分组结构（例如对客户进行细分），常见算法包括K-Means、层次聚类等。
1、逻辑回归
逻辑回归是一种广泛应用于分类问题的统计方法，尽管其名称包含"回归"，但它实际上也是一种用于二分类或多分类问题的分类算法 。逻辑回归通过估计一个事件发生的概率来预测类别标签，由于其简单、易于理解和实现，以及在分类问题中的有效性，成为了机器学习和数据分析中非常流行的算法。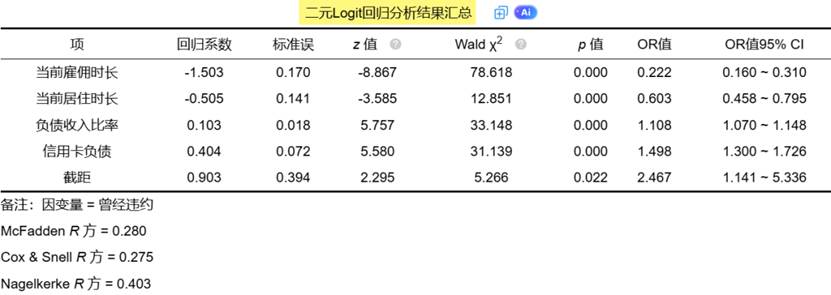
2、Fisher线性判别
判别分析一种机器学习算法，其用于在分类确定前提下，根据数据的特征研究数据归类问题。判别分析有多种，比如距离判别，Fisher判别（典型判别，线性判别分析、Fisher线性判别），Bayes判别等。其中Fisher判别使用频率最高，原因在于其对数据特征的分布没有任何限制，SPSSAU默认使用Fisher线性判别进行分析。
3、决策树等机器学习方法
决策树、随机森林、朴素贝叶斯、KNN 等可归类为机器学习进行分类。SPSSAU输出部分结果示例如下：
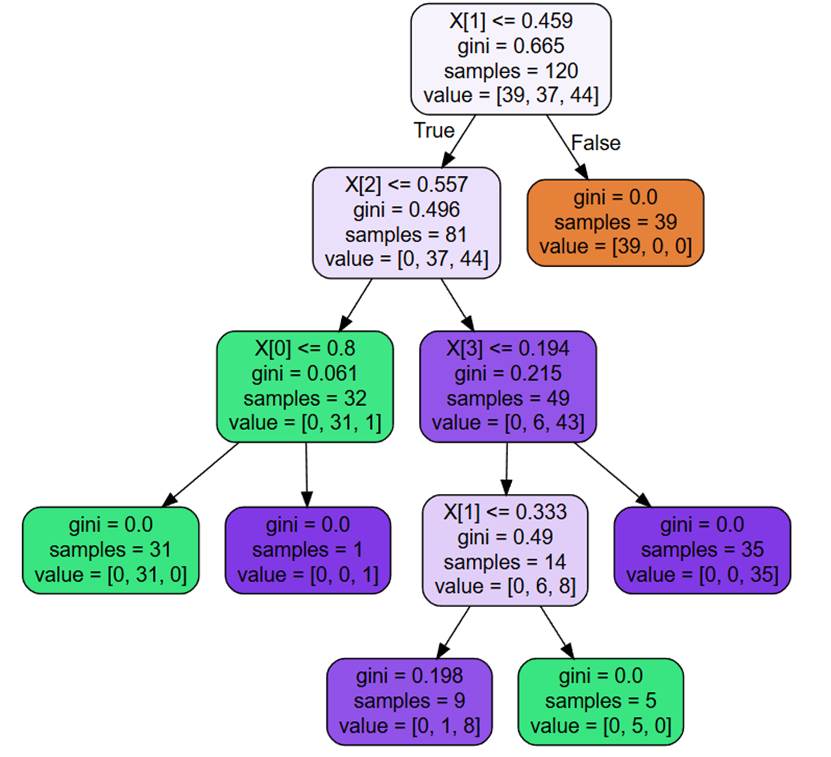SPSSAU【机器学习】模块方法如下（点击方法名称可跳转至相关方法帮助手册）：
|------------------------------------------------------------------------------------|----------------------------|
| 方法名称 | 核心功能 |
| 决策树 | 通过树形结构进行决策分类或回归，模型直观易懂。 |
| 随机森林 | 集成多棵决策树，通过投票提高预测准确性和稳定性。 |
| KNN | K近邻算法，根据最近样本的类别来判断新样本的类别。 |
| 朴素贝叶斯 | 基于贝叶斯定理，假设特征独立，进行高效的概率分类。 |
| 支持向量机 | 寻找最优分类边界，擅长处理高维数据和小样本分类。 |
| 神经网络 | 模拟人脑神经元连接，能拟合极其复杂的非线性模式。 |
| logistic回归 | 经典的分类算法，预测二分类或多分类事件的概率。 |
| apriori关联分析 | 从数据中挖掘频繁项集，发现"如果A则B"的关联规则。 |
| XGBoost | 一种高效、强大的梯度提升决策树算法，常获竞赛冠军。 |
| GBDT | 梯度提升决策树，通过迭代训练弱分类器来提升模型性能。 |
| Adaboost | 自适应增强算法，通过调整样本权重迭代提升分类精度。 |
| 极端随机树 | 随机森林的变体，引入更多随机性以进一步降低过拟合。 |
| CatBoost | 擅长处理类别特征的无偏梯度提升算法，无需大量预处理。 |
| LightGBM | 轻量的梯度提升框架，训练速度快且内存消耗低。 |
4、K-Means聚类
K-Means聚类是一种经典的无监督算法。其核心思想是预先指定目标簇数K，通过迭代计算，不断更新每个簇的中心点，并将每个数据点分配到距离其最近的簇中，最终使得簇内样本的相似度最高（距离最小），而簇间差异最大。
SPSSAU【进阶方法】模块提供的【聚类】分析，包括K-Means聚类、K-modes聚类、K-prototype聚类，只需要把定量/定类变量拖拽至右侧对应分析框即可进行相应的聚类分析。SPSSAU操作如下图：
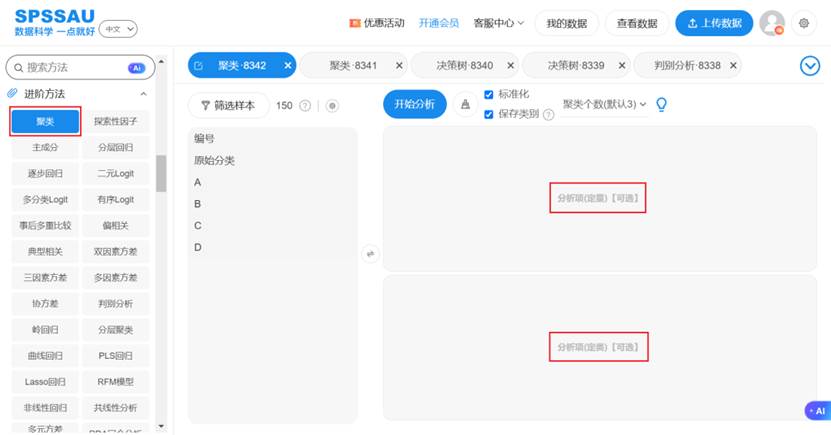
SPSSAU输出K-Means聚类分析部分结果如下：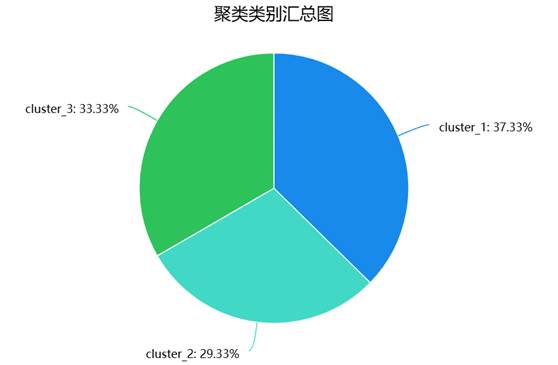
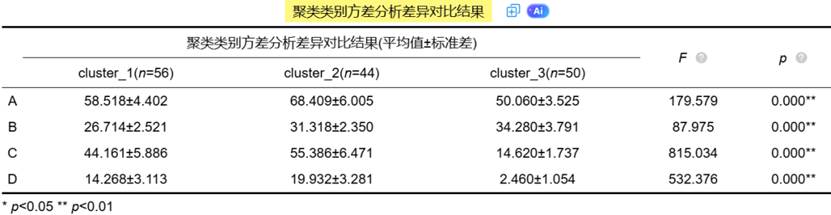
5、分层聚类
从分析角度上看，聚类分析可分为两种，一种是按样本（或个案）聚类，此类聚类的代表是K-Means聚类方法；另外一种是按变量（或标题）聚类，此类聚类的代表是分层聚类。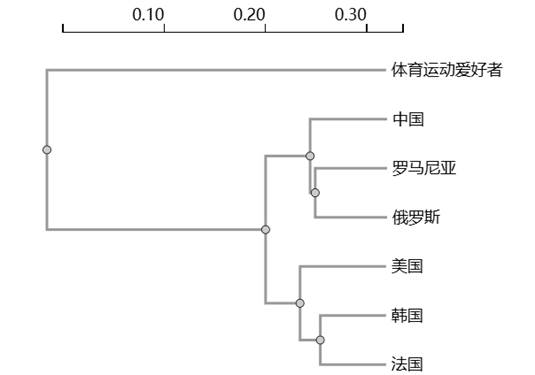
五、统计分析模型
在数学建模中，除了上述综合性模型外，许多问题的局部求解还会涉及一些基础但关键的统计分析知识点。这些方法虽然原理相对简单，但它们是构建严谨数学模型、验证假设和分析数据关系的基石。简单介绍如下（点击方法名称跳转至详细教程）：
|--------------------------------------------------------------------------------------------------------------------------------------------------------|--------------------------------|
| 方法名称 | 核心目的 |
| 相关性分析 | 衡量多个变量之间的关联强度与方向。 |
| 差异性分析 | 检验两个或多个组别在某指标上是否存在显著差异。 |
| 线性回归分析 | 建立因变量与一个/多个自变量的线性关系模型，用于预测或解释。 |
| 结构方程模型 | 检验多个变量之间复杂的因果路径关系（包含潜变量）。 |
| 主成分分析 | 对原始多变量进行降维，提取少数几个综合成分（主成分）。 |
| 因子分析 | 从多个可测变量中提取背后潜在的公共因子，以解释其内在结构。 |
统计分析高频分析方法以往也总结过，更详细的介绍可以查看下方文章：