大家好, 我是印刻君. 今天我们来聊一个很多 AI 爱好者容易困惑的问题, 函数, 向量, 矩阵与神经网络之间到底是什么关系?
不少朋友接触 AI 时, 常会被一连串数学概念绕得晕头转向. 上一秒是 "函数", 下一秒是 "向量", 过一会又出现 "矩阵", 紧接着又是 "神经网络". 自己似乎每个概念都懂一点, 但放在一起就成了一团乱麻.
今天, 我们就从最基础的概念出发, 一步步把这些知识点串联起来, 梳理出一条清晰的逻辑链, 帮你看懂这些数学概念的关系.
阅读本文前, 最好对向量, 矩阵有一个基础了解, 阅读体验会更好:
不熟悉向量, 可以看我的文章: 不再费脑,写给爱好者的 AI 向量 (Vector) 入门课
不熟悉矩阵, 可以看我的文章: 不再费脑, 写给 AI 爱好者的矩阵 (Matrix) 入门指南
1 从函数说起, AI 的本质是用函数刻画世界规律
要理清这些概念, 我们首先要回到最根本的数学工具函数 上. 其实人工智能的核心目标很简单, 用函数刻画现实世界的规律.
这个目标可以简化为 "输入-输出" 的转换过程, 输入是 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x, 输出是经过函数计算的结果 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) f(x) </math>f(x), 中间的转换过程就是函数.
这里的输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 可以是现实世界的各种数据, 比如苹果的重量, 图片的像素值等; 而 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) f(x) </math>f(x) 则是我们想要得到的结果, 比如苹果的总价, 图片的分类标签 (是猫还是狗) 等. AI 要做的核心工作, 就是找出合适的 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) f(x) </math>f(x), 完成从输入到输出的转换.
需要注意的是, 现代 AI 并没有找到绝对精准的函数, 找到的只是近似的函数, 这种 "近似" 涉及到概率论的相关知识, 本文为了聚焦核心逻辑链, 暂不展开这部分内容.
2 一元函数与线性关系
要找 AI 需要的函数, 我们先从最简单的规律入手. 现实中最容易理解的规律是线性关系, 对应的数学工具是线性函数, 表达式为 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = w x + b f(x) = wx + b </math>f(x)=wx+b. 这里的 <math xmlns="http://www.w3.org/1998/Math/MathML"> w w </math>w 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b 是两个关键参数.
- <math xmlns="http://www.w3.org/1998/Math/MathML"> w w </math>w 是 "权重", 可以理解为 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 对结果的影响程度.
- b 是 "偏置", 可以理解为不依赖输入的固定的基准值.
举生活例子, 假如 1 斤苹果卖 5 元钱, 那么买 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x 斤苹果的总价 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) f(x) </math>f(x), 就可以用线性函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = 5 x + 0 f(x) = 5x + 0 </math>f(x)=5x+0 表示.
- 这里的权重 <math xmlns="http://www.w3.org/1998/Math/MathML"> w = 5 w=5 </math>w=5, 代表每斤苹果的价格对总价的影响;
- 偏置 <math xmlns="http://www.w3.org/1998/Math/MathML"> b = 0 b=0 </math>b=0, 因为买 0 斤苹果时, 总价自然为 0, 没有额外的固定成本. (如果例子是打车, 起步费为 10 块, 偏置就是 10).
3 单输出的多元函数与向量
刚才苹果的例子,是 "单输入 (单元), 单输出" 的情况. 但实际生活中, 情况其实更复杂, 我们更容易遇见的 "多输入 (多元), 单输出" 的情况.
比如通过 "房间数量, 房间面积, 楼层高度" 这三个输入, 预测 "房屋总价" 这一个输出.
这时候我们需要用 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 1 x_1 </math>x1, <math xmlns="http://www.w3.org/1998/Math/MathML"> x 2 x_2 </math>x2 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 3 x_3 </math>x3 分别代表三个输入, 对应的函数表达式为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x 1 , x 2 , x 3 ) f(x_1, x_2, x_3) </math>f(x1,x2,x3)
<math xmlns="http://www.w3.org/1998/Math/MathML"> = w 1 x 1 + w 2 x 2 + w 3 x 3 + b \quad = w_1x_1 + w_2x_2 + w_3x_3 + b </math>=w1x1+w2x2+w3x3+b
其中 <math xmlns="http://www.w3.org/1998/Math/MathML"> w 1 w_1 </math>w1, <math xmlns="http://www.w3.org/1998/Math/MathML"> w 2 w_2 </math>w2, <math xmlns="http://www.w3.org/1998/Math/MathML"> w 3 w_3 </math>w3 分别是三个输入对应的权重 (比如 <math xmlns="http://www.w3.org/1998/Math/MathML"> w 2 w_2 </math>w2 代表房间面积对房价的影响力度), <math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b 是偏置项.
如果推广到 <math xmlns="http://www.w3.org/1998/Math/MathML"> n n </math>n 个输入的场景, 函数表达式写为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x 1 , x 2 , . . . x n ) f(x_1, x_2, ...x_n) </math>f(x1,x2,...xn)
<math xmlns="http://www.w3.org/1998/Math/MathML"> = w 1 x 1 + w 2 x 2 + . . . + w n x n + b \quad = w_1x_1 + w_2x_2 + ... + w_nx_n + b </math>=w1x1+w2x2+...+wnxn+b
我们发现, 当输入变量增多后, 表达式就变得冗长了, 这时候需要一种工具来简化表达.
向量就是这个关键工具:
- 我们可以把所有输入 <math xmlns="http://www.w3.org/1998/Math/MathML"> [ x 1 , x 2 , . . . , x n ] [x_1, x_2, ..., x_n] </math>[x1,x2,...,xn] 打包, 用 <math xmlns="http://www.w3.org/1998/Math/MathML"> x \boldsymbol{x} </math>x (小写字母加粗) 表示, 它就是输入向量;
- 再把所有权重 <math xmlns="http://www.w3.org/1998/Math/MathML"> [ w 1 , w 2 , . . . , w n ] [w_1, w_2, ..., w_n] </math>[w1,w2,...,wn] 打包, 用 <math xmlns="http://www.w3.org/1998/Math/MathML"> w \boldsymbol{w} </math>w (小写字母加粗) 表示, 它就是权重向量.
通过点乘运算 (本质是对应元素相乘后求和), 原本冗长的表达式就被简化为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f ( x ) = w ⋅ x + b f(\boldsymbol{x}) = \boldsymbol{w} \cdot \boldsymbol{x} + b </math>f(x)=w⋅x+b
这里可以明确一个关系, 一元函数是多元函数的特殊情况, 当输入向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> x \boldsymbol{x} </math>x 只有 1 维时, 多元函数就退化成了一元函数.
这里向量的核心作用, 就是把多个参数打包整合, 让复杂的函数表达式更简洁, 更通用.
4 多输出的多元函数与矩阵
前面预测 "房屋总价" 的例子是 "多输入, 单输出", 但现实生活中, 我们还常常会遇到 "多输入, 多输出" 的场景.
同样以房屋为例子, 我们需要通过 "房间数量, 房间面积, 楼层高度" 这三个输入, 预测 "房屋总价, 月租金额" 两个输出.
这种情况下, 我们需要为每个输出单独构建一个多元函数, 形成方程组:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> { f 1 ( x 1 , x 2 , x 3 ) = w 11 x 1 + w 12 x 2 + w 13 x 3 + b 1 f 2 ( x 1 , x 2 , x 3 ) = w 21 x 1 + w 22 x 2 + w 23 x 3 + b 2 \begin{cases} f_1(x_1, x_2, x_3) = w_{11}x_1 + w_{12}x_2 + w_{13}x_3 + b_1 \\ f_2(x_1, x_2, x_3) = w_{21}x_1 + w_{22}x_2 + w_{23}x_3 + b_2 \end{cases} </math>{f1(x1,x2,x3)=w11x1+w12x2+w13x3+b1f2(x1,x2,x3)=w21x1+w22x2+w23x3+b2
其中:
- <math xmlns="http://www.w3.org/1998/Math/MathML"> f 1 ( x 1 , x 2 , x 3 ) f_1(x_1, x_2, x_3) </math>f1(x1,x2,x3) 是预测房屋总价的函数, 而 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 2 ( x 1 , x 2 , x 3 ) f_2(x_1, x_2, x_3) </math>f2(x1,x2,x3) 是预测月租金额的函数;
- <math xmlns="http://www.w3.org/1998/Math/MathML"> w i j w_{ij} </math>wij 表示第 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 个输出对应的第 <math xmlns="http://www.w3.org/1998/Math/MathML"> j j </math>j 个输入的权重 (比如 <math xmlns="http://www.w3.org/1998/Math/MathML"> w 12 w_{12} </math>w12是房间面积 <math xmlns="http://www.w3.org/1998/Math/MathML"> x 2 x_2 </math>x2 对房屋总价 <math xmlns="http://www.w3.org/1998/Math/MathML"> f 1 f_1 </math>f1 的影响权重);
- <math xmlns="http://www.w3.org/1998/Math/MathML"> b 1 b_1 </math>b1 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> b 2 b_2 </math>b2 则是对应两个输出的偏置项
观察这个方程组会发现, 如果我们把所有的 <math xmlns="http://www.w3.org/1998/Math/MathML"> w i j w_{ij} </math>wij 提取出来, 会形成一个 2 行 3 列的 "权重阵列", 再把两个输出, 三个输入, 两个权重打包成向量, 方程组就开始用矩阵乘法简化表示:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ f 1 f 2 ] = [ w 11 w 12 w 13 w 21 w 22 w 23 ] ⋅ [ x 1 x 2 x 3 ] + [ b 1 b 2 ] \begin{bmatrix} f_1 \\ f_2 \end{bmatrix} = \begin{bmatrix} w_{11} & w_{12} & w_{13} \\ w_{21} & w_{22} & w_{23} \\ \end{bmatrix} \cdot \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} b_1 \\ b_2 \end{bmatrix} </math>[f1f2]=[w11w21w12w22w13w23]⋅ x1x2x3 +[b1b2]
我们把这个 "权重阵列" 称为矩阵 ,用大写粗体字母 <math xmlns="http://www.w3.org/1998/Math/MathML"> W \boldsymbol{W} </math>W 表示, 同时用 <math xmlns="http://www.w3.org/1998/Math/MathML"> f \boldsymbol{f} </math>f, <math xmlns="http://www.w3.org/1998/Math/MathML"> x \boldsymbol{x} </math>x 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> b \boldsymbol{b} </math>b 表示竖着排的输出向量, 输入向量和偏置向量, 方程组可以简化为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f = W ⋅ x + b \boldsymbol{f} = \boldsymbol{W} \cdot \boldsymbol{x} + \boldsymbol{b} </math>f=W⋅x+b
这里要明确核心关系, 矩阵 本质是向量的组合, 把多个向量横着或者竖着排, 就形成了矩阵. 反过来, 向量也可以看成是 1 行 n 列, 或者 n 行 1 列的矩阵.
矩阵的核心作用, 就是把 "多输入, 多输出" 的复杂场景, 用一套标准的运算统一整合. 大幅度提升 AI 处理复杂任务的效率.
5 非线性关系与激活函数
前面我们讨论的都是线性关系, 但现实生活的规律大多数都是非线性的.
举个例子, 人的年龄和收入的关系. 20 岁之前, 收入可能很低甚至为零; 20~40 岁之间, 收入会快速增长; 40岁之后, 收入可能趋于稳定甚至缓慢下降.
这种 "不按比例线性变化" 的关系, 就是非线性关系. 显然,线性函数无法精准刻画这种复杂的规律.
这时候, 激活函数 就成了解决问题的关键, 我们在原有线性计算的基础上, 加入一个激活函数 <math xmlns="http://www.w3.org/1998/Math/MathML"> g g </math>g, 函数表达式变为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f = g ( W ⋅ x + b ) \boldsymbol{f} = g(\boldsymbol{W} \cdot \boldsymbol{x} + \boldsymbol{b}) </math>f=g(W⋅x+b)
激活函数的作用, 就是给线性计算的结果, 加上 "非线性" 转换, 让函数拥有刻画复杂规律的能力.
常见的激活函数有:
Sigmoid, 可以将结果映射到 0 和 1 之间, 适合概率预测;
ReLU, 在输入为正时直接输出, 为负是输出 0, 是当前 AI 最常用的激活函数之一.
而 "线性计算 + 非线性激活" 的组合, 就是神经网络中最基础的神经元, 它模拟了生物接受信号, 处理信号的过程, 如果用神经网络结构图表示, 单个神经元结构如下:
- 单输入的神经元:

- 多输入的神经元:
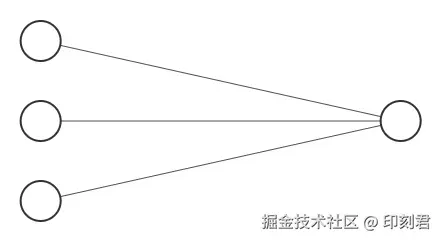
6 多层堆叠与神经网络
可能有朋友会问, 加入一次非线性转换, 就够拟合所有复杂规律了吗? 答案是 "不够".
现实世界中的很多规律, 比如图像识别 (判断图片是猫还是狗), 自然语言理解 (从文字中读懂情感) 这类复杂任务, 其复杂程度远超一次非线性转换能刻画的范围.
那该怎么办呢? 我们的做法是: 把 "线性计算 + 非线性激活" 的模块, 一层一层地叠加. 这就是 "多层神经网络" 的核心逻辑.
比如一个 2 层的神经网络, 它的函数表达式为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> f = W 2 ⋅ g ( W 1 ⋅ x + b 1 ) + b 2 \boldsymbol{f} = \boldsymbol{W_2} \cdot g(\boldsymbol{W_1} \cdot \boldsymbol{x} + \boldsymbol{b_1}) + \boldsymbol{b_2} </math>f=W2⋅g(W1⋅x+b1)+b2
这个过程中:
- 第一层神经元先对原始特征 <math xmlns="http://www.w3.org/1998/Math/MathML"> x \boldsymbol{x} </math>x 做初步的特征提取 (比如在图像检测中, 提取边缘/纹理等简单特征. 经过激活函数处理后, 把结果传递到第二层;
- 第二层神经元, 对第一层的结果做更复杂的特征整合 (比如把边缘, 纹理等特征整合为 "眼睛" "耳朵" 等更高级的特征), 最终输出预测结果.
这个过程, 假设最开始的输入是 6 个, 第一层输出是 3 个, 第二层输出是 1 个, 则神经网络结构图为:
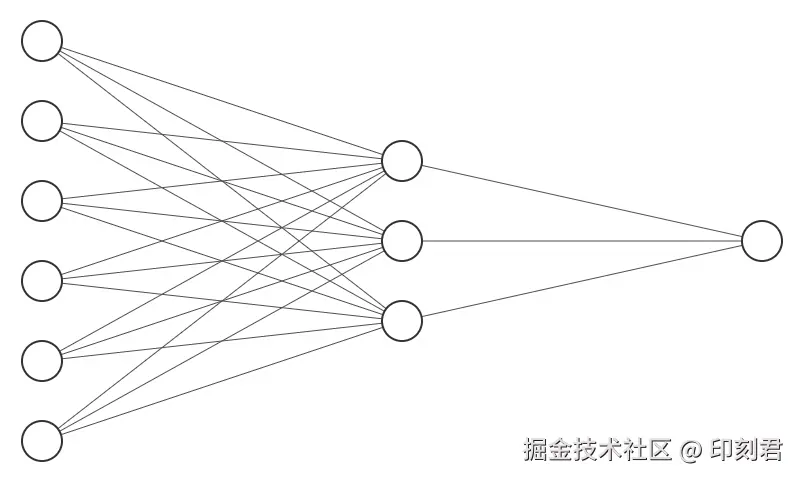
层数堆叠越多, 结构越来越复杂, 这就是神经网络:
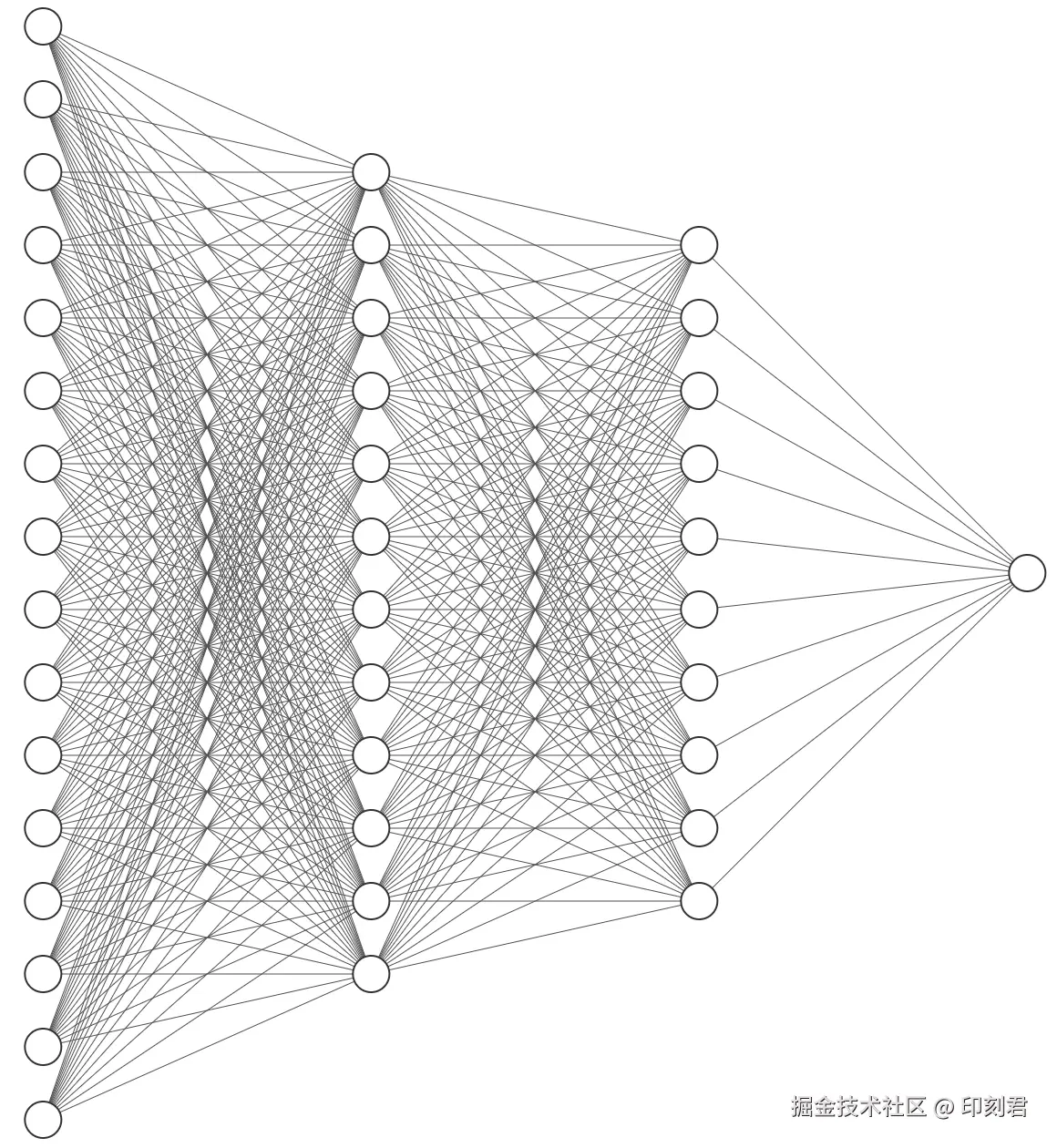
当前主流的大模型, 堆叠的层数更是达到了几百甚至上千层.
总结
AI 的核心目的是刻画世界的规律, 而函数, 向量, 矩阵, 神经网络是达成这个目的的数学工具. 向量被用来简化多输入的表达, 矩阵被用来整合多输出的运算, 叠加 "线性计算 + 非线性激活" 则形成了神经网络.
我是印刻君,一位探索 AI 的前端程序员,关注我,让 AI 知识有温度,技术落地有深度.