一、背景
本文提出了一种相对简单的缺陷校正算法,仅需7×7的原始彩色滤光片阵列数据核即可有效校正多种缺陷类型。该自适应边缘算法具有高质量、占用图像行数少、适应性强且独立于其他板载DSP算法的特点。实验结果表明,相较于传统一维校正方法,该算法在高频图像区域的校正效果显著提升
二、原理:
由于相邻像素能为缺陷像素的插值提供最佳信息,希望先确定该区域的边缘方向,再利用该方向上的两个相邻像素来估算缺失像素值。bayer结构下与缺陷颜色相同且最近的已知信息至少相隔两个像素,插值精度会随着与缺陷位置距离的增加而急剧下降
三、算法整体流程(在 7×7 Bayer 原始窗口内完成)
1、方向向量提取
以缺陷像素 d[m0,n0] 为中心,按 4 个方向抽 7 点向量: d1:垂直 d2:主对角 d3:水平 d4:副对角

d 1 ( n ) = a ( m 0 , n 0 − 3 ) , . . . . a ( m 0 , n 0 ) , . . . , a ( m 0 , n 0 + 3 ) d_1(n)=a(m_0,n_0-3),....a(m_0,n_0),...,a(m_0,n_0+3) d1(n)=a(m0,n0−3),....a(m0,n0),...,a(m0,n0+3)
d 2 ( n ) = a ( m 0 − 3 , n 0 + 3 ) , . . . . a ( m 0 , n 0 ) , . . . , a ( m 0 + 3 , n 0 − 3 ) d_2(n)=a(m_0-3,n_0+3),....a(m_0,n_0),...,a(m_0+3,n_0-3) d2(n)=a(m0−3,n0+3),....a(m0,n0),...,a(m0+3,n0−3)
d 3 ( n ) = a ( m 0 − 3 , n 0 ) , . . . . a ( m 0 , n 0 ) , . . . , a ( m 0 + 3 , n 0 ) d_3(n)=a(m_0-3,n_0),....a(m_0,n_0),...,a(m_0+3,n_0) d3(n)=a(m0−3,n0),....a(m0,n0),...,a(m0+3,n0)
d 4 ( n ) = a ( m 0 − 3 , n 0 − 3 ) , . . . . a ( m 0 , n 0 ) , . . . , a ( m 0 + 3 , n 0 + 3 ) d_4(n)=a(m_0-3,n_0-3),....a(m_0,n_0),...,a(m_0+3,n_0+3) d4(n)=a(m0−3,n0−3),....a(m0,n0),...,a(m0+3,n0+3)
备注: 如果缺陷是整列缺陷,则不使用垂直向量 d1。
2、向量内部坏点处理
若某位置仍是坏点,用"隔 2 点镜像"快速插值补全,避免把台阶平均掉。 4 条向量全部变为"无坏点"的连续信号。确保向量一侧的阶跃函数不会被平均到另一侧。这可确保在算法后续阶段,该向量不会被错误地选为边缘方向
3、跨颜色平面归一化(核心)
对每条向量取最近同色点 d i [ − 2 ] d_i[-2] di[−2]、d_i\[+2\] 做基准;向量点 做基准; 向量点 做基准;向量点di\[−1\] 和 和 和di\[+1\](即距离缺陷最近的点,计算异色平面在缺陷两侧的一阶导数 σ i ( − 1 ) \sigma_{i}(-1) σi(−1), σ i ( 1 ) \sigma_{i}(1) σi(1);
σ i ( − 1 ) = d i ( − 1 ) − d i ( − 3 ) 2 \sigma_{i}(-1)=\frac{d_{i}(-1)-d_{i}(-3)}{2} σi(−1)=2di(−1)−di(−3)
σ ( 1 ) = d i ( 1 ) − d i ( 3 ) 2 \sigma(1)=\frac{d_{i}(1)-d_{i}(3)}{2} σ(1)=2di(1)−di(3)
方向导数用于关联缺陷颜色平面附近的点,定义新的向量来估计样本点相对于缺陷颜色平面的位置,把异色点 d i ^ ( − 1 ) \hat{d_{i}}(-1) di^(−1), d i ^ ( 1 ) \hat{d_{i}}(1) di^(1)按导数偏移量"搬"到缺陷颜色平面,得到归一化值
d i ^ ( − 1 ) = d i ( − 2 ) + σ i ( − 1 ) \hat{d_{i}}(-1)={d_{i}(-2)+\sigma_{i}(-1)} di^(−1)=di(−2)+σi(−1)
d i ^ ( 1 ) = d i ( 2 ) + σ i ( 1 ) \hat{d_{i}}(1)={d_{i}(2)+\sigma_{i}(1)} di^(1)=di(2)+σi(1)
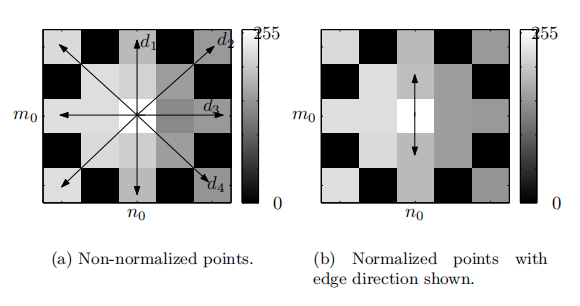
该算法无需知晓特定像素的实际滤色值------它仅需知道拜耳模式在任意方向上会采样两种颜色。
4、 边缘加权融合
加权融合公式如下:
β i = 1 − σ i k ∑ σ i k I − 1 \beta_{i}=\frac{1-\frac{\sigma_{i}^{k}}{\sum\sigma_{i}^{k}}}{I-1} βi=I−11−∑σikσik
其中,计算向量灰度差
σ i = ∣ d i ( − 1 ) − d i ( 1 ) ∣ \sigma_{i}=|d_i(-1)-d_i(1)| σi=∣di(−1)−di(1)∣
指数k可调节以改变算法对di[n]差异的敏感度,敏感度随k增大而增强。使用向量的数量用I表示。与边缘方向对齐最接近的向量(即|di[−1]−di[+1]|最小值)将具有最大 ξi 权重。
缺陷补偿
a ^ ( m 0 , n 0 ) = ∑ β i ( ∣ d i ( − 1 ) − d i ( 1 ) ∣ 2 ) \hat{a}(m_0,n_0)=\sum\beta_i(\frac{|d_i(-1)-d_i(1)|}{2}) a^(m0,n0)=∑βi(2∣di(−1)−di(1)∣)
最后,校正数据修正,满足以下条件校正,否则保留原始缺陷值,防止高频区"修坏"
a ( m 0 , n 0 ) = a ^ ( m 0 , n 0 ) , i f ∣ a ^ ( m 0 , n 0 ) − a ( m 0 , n 0 ) ∣ < e C + t C a(m_0,n_0)=\hat{a}(m_0,n_0),if|\hat{a}(m_0,n_0)-{a}(m_0,n_0)|<eC+tC a(m0,n0)=a^(m0,n0),if∣a^(m0,n0)−a(m0,n0)∣<eC+tC
e是工厂标定最大偏差,t是 混叠容限
5、处理效果
