动机
当前大模型的强化学习训练(RLHF、RLAIF等)往往需要同时优化多个目标:回答要准确(correctness)、格式要规范(format compliance)、长度要合适(length constraint)、足够有帮助(helpfulness)等,就像给学生评定综合成绩,需要同时考虑语文、数学、体育等多门课程
常见的多奖励优化方法(如 GRPO)的做法是:先把各科成绩加权汇总,再对总分做归一化计算优势函数。这看起来很合理,但实际训练中会出现一个致命问题:优势塌缩(advantage collapse)------不同的奖励组合被映射成相同的优势值,模型看不到这些组合之间的细微差异,导致训练信号失真
对此英伟达提出了 GDPO(Group reward-Decoupled Normalization Policy Optimization),其解决方案为:先对每个奖励单独做归一化,再加权融合,最后再做批归一化
漫画版介绍
https://blog.csdn.net/qq_36671160/article/details/156837211
论文标题
GDPO: Group reward-Decoupled Normalization Policy Optimization for Multi-reward RL Optimization
论文地址
https://arxiv.org/pdf/2601.05242
作者背景
英伟达
代码地址
https://github.com/NVlabs/GDPO/tree/main/trl-GDPO
问题分析
优势坍缩
论文给出了一个直观的例子:假设有两个二元奖励 r₁, r₂ ∈ {0,1},每个问题采样两条轨迹。虽然存在 6 种不同的奖励组合(忽略顺序),但 GRPO 归一化后只剩下 2 个不同的优势组:
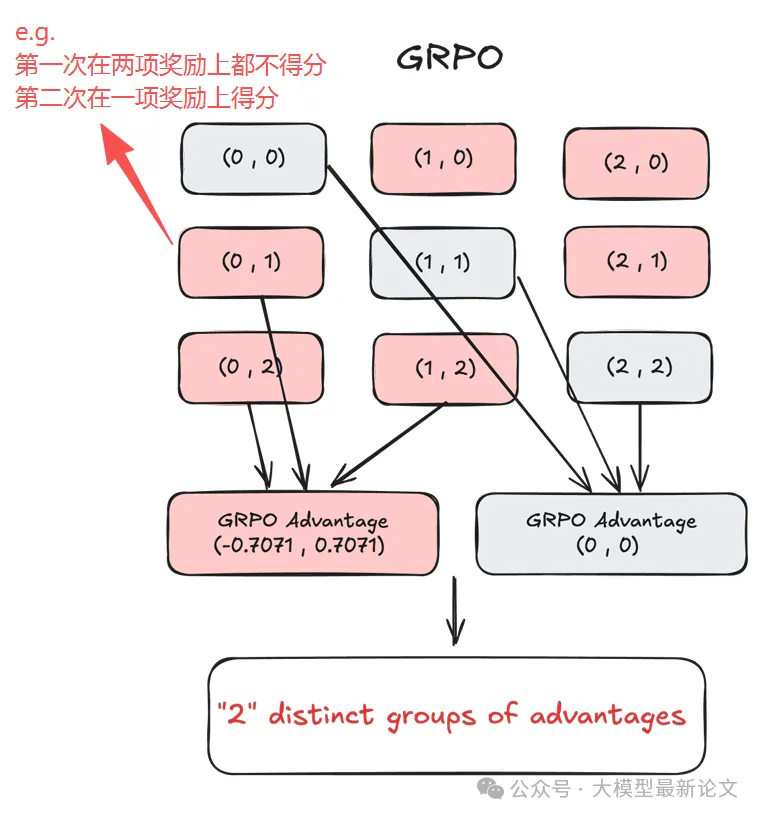
这就出问题了:直觉上 (0,2) 应该比 (0,1) 产生更强的学习信号(因为前者拿到了两个奖励,后者只有一个),但 GRPO 让它们完全相同!
更糟的是,(1,1) 看起来两条轨迹表现相同,但它可能来自:
r₁ = (1,1), r₂ = (0,0) ------ 都擅长目标1,但完全忽略目标2
r₁ = (0,0), r₂ = (1,1) ------ 都擅长目标2,但完全忽略目标1这两种情况有本质区别,但 GRPO 都给它们赋予零优势值,模型学不到任何信号
规模越大问题越严重
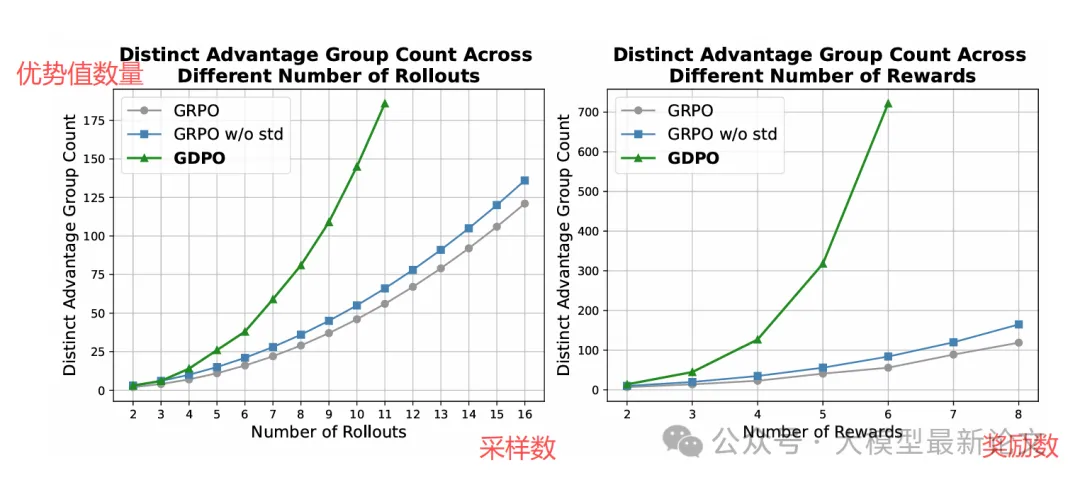
最近还有一些工作如 Dr.GRPO 和 DeepSeek-v3.2 采用了一种 GRPO 的变体,移除了标准差规范化项,使得:
A_sum = (r_sum - mean_group(r_sum)) / std_group(r_sum)尽管此修改原本是为了缓解问题级别的难度偏差,但从表面看,它似乎也解决了上述问题:移除标准差规范化后,(0, 1) 与 (0, 2) 的优势值变成了 (−0.5, 0.5) 与 (−1.0, 1.0)。然而可惜的是,当 rollout 次数或奖励数量更多时,优势组的多样性仅有少量提升
真实训练中的崩溃
优势塌缩不只是理论问题,会直接导致实际训练失败(细节见下文【实验结果】)
GDPO的"三步归一化"方案
GDPO 的改进分为三步:
第1步:独立归一化每个奖励
对每个奖励维度单独做组内标准化:
A₁ = (r₁ - mean_group(r₁)) / std_group(r₁)
A₂ = (r₂ - mean_group(r₂)) / std_group(r₂)
...
Aₙ = (rₙ - mean_group(rₙ)) / std_group(rₙ)第2步:加权融合
将标准化后的优势值按权重相加:
A_sum = w₁·A₁ + w₂·A₂ + ... + wₙ·Aₙ第3步:批量优势归一化
在整个 batch 的所有轨迹上再做一次归一化:
Â_sum = (A_sum - mean_batch(A_sum)) / (std_batch(A_sum) + ε)为什么需要第3步?
- 确保优势的数值范围稳定,不会因为奖励数量增加而爆炸
- 实验表明去掉这一步会导致训练不稳定,有时甚至完全失败
回到之前的例子,GDPO 将会产生 3 个不同的优势组,更准确地区分了不同轨迹的表现水平
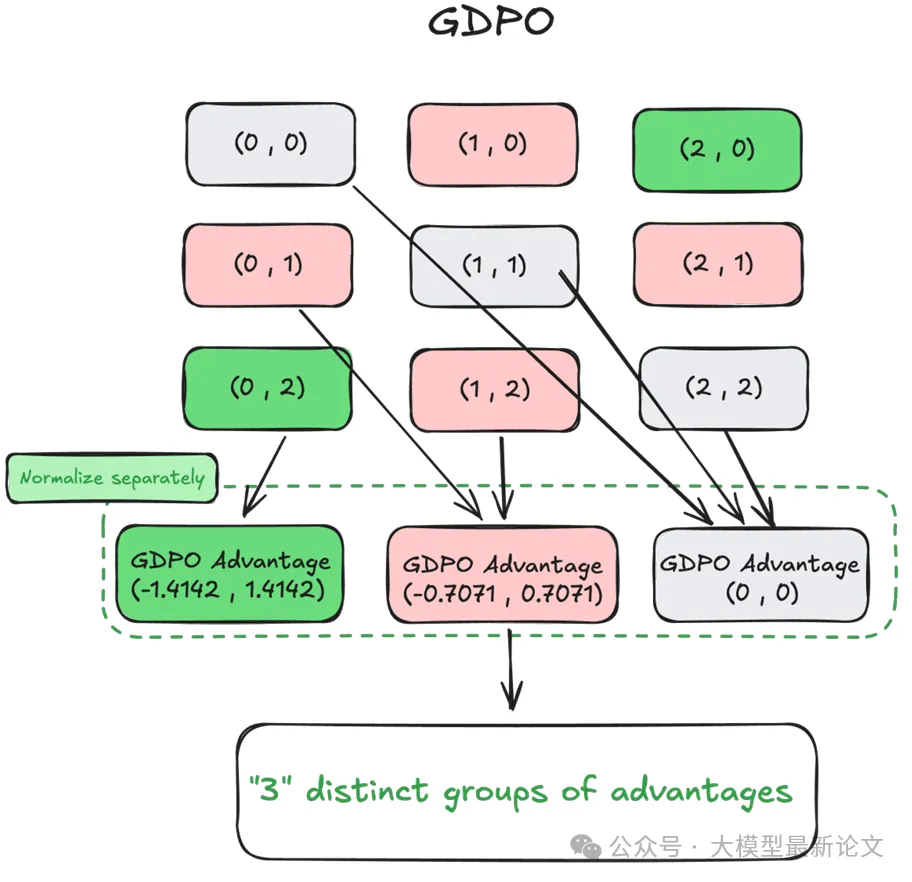
更重要的是,对于之前的 (1,1) 情况:
r₁=(1,1), r₂=(0,0) → GDPO 会给出正向的 A₁ 信号
r₁=(0,0), r₂=(1,1) → GDPO 会给出正向的 A₂ 信号奖励优先级调整
前面我们假设所有奖励同等重要(权重都是1)。但实际应用中,我们往往有优先级,例如:
- 准确性 > 长度约束
宁可长一点,也不能错 - 安全性 > 帮助性
宁可拒绝回答,也不能输出有害内容
直觉的做法是:给重要的奖励更高的权重 w。但论文发现,当两个目标难度差异很大时,调权重往往不管用(细节见下文【实验结果】)
对此,作者提出了一个更有效的策略:把简单的奖励条件化在困难的奖励之上。定义条件化长度奖励:
R̃_length = R_length if R_correct >= threshold else0即只有在答对的前提下,长度约束才有意义;答错了,再短也不给奖励
实验结果
作者在三类典型任务上验证了 GDPO 的有效性:
任务1:工具调用(Tool Calling)
数据集:ToolRL (4000条训练样本,来自 ToolACE、Hammar、xLAM)
模型:Qwen2.5-1.5B 和 3B
奖励:格式奖励 R_format ∈ {0,1},正确性奖励 R_correct ∈ [-3, 3]
评估:BFCL-v3 排行榜(包含单步/多步/多工具等多种场景)
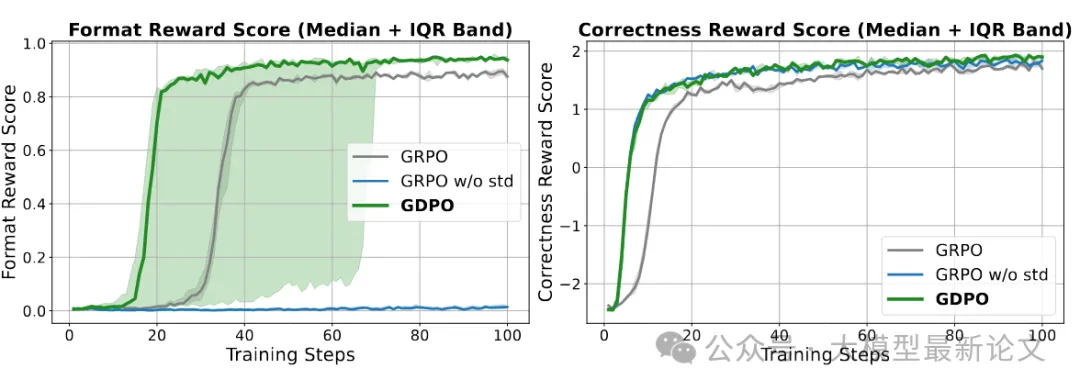
实验结论:
- GDPO 在格式和正确性奖励上都收敛到更高值
- GDPO 早期改进更快,后期稳定性更好
- GRPO w/o std 虽然正确性接近 GDPO,但格式约束完全失败
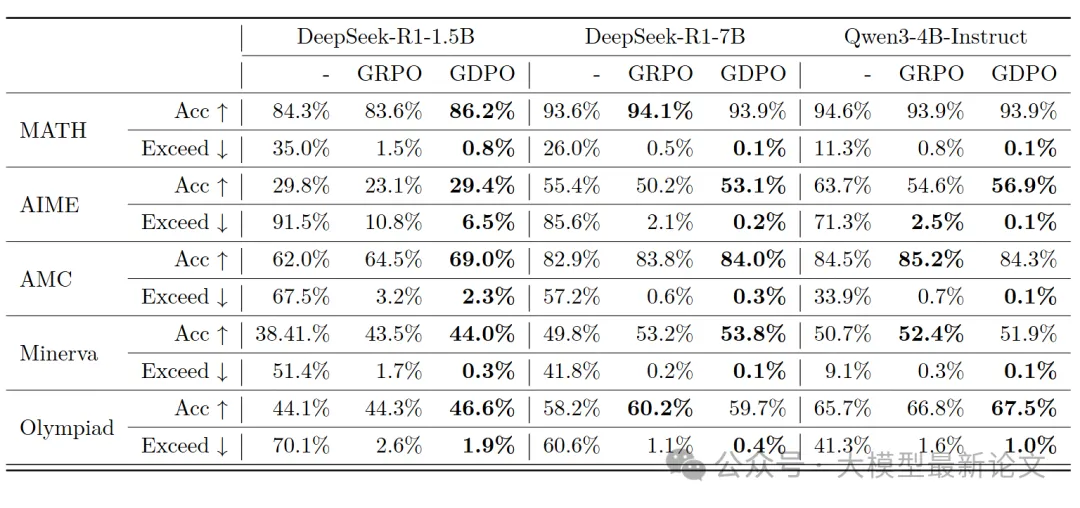
任务2:数学推理(Math Reasoning)
- 数据集:DeepScaleR-Preview (40K 竞赛级数学题)
- 模型:DeepSeek-R1-1.5B、7B 和 Qwen3-4B
- 奖励:正确性 R_correct ∈ {0,1},长度约束 R_length ∈ {0,1} (限制≤4000 tokens)
- 评估:MATH、AIME、AMC、Minerva、Olympiad Bench
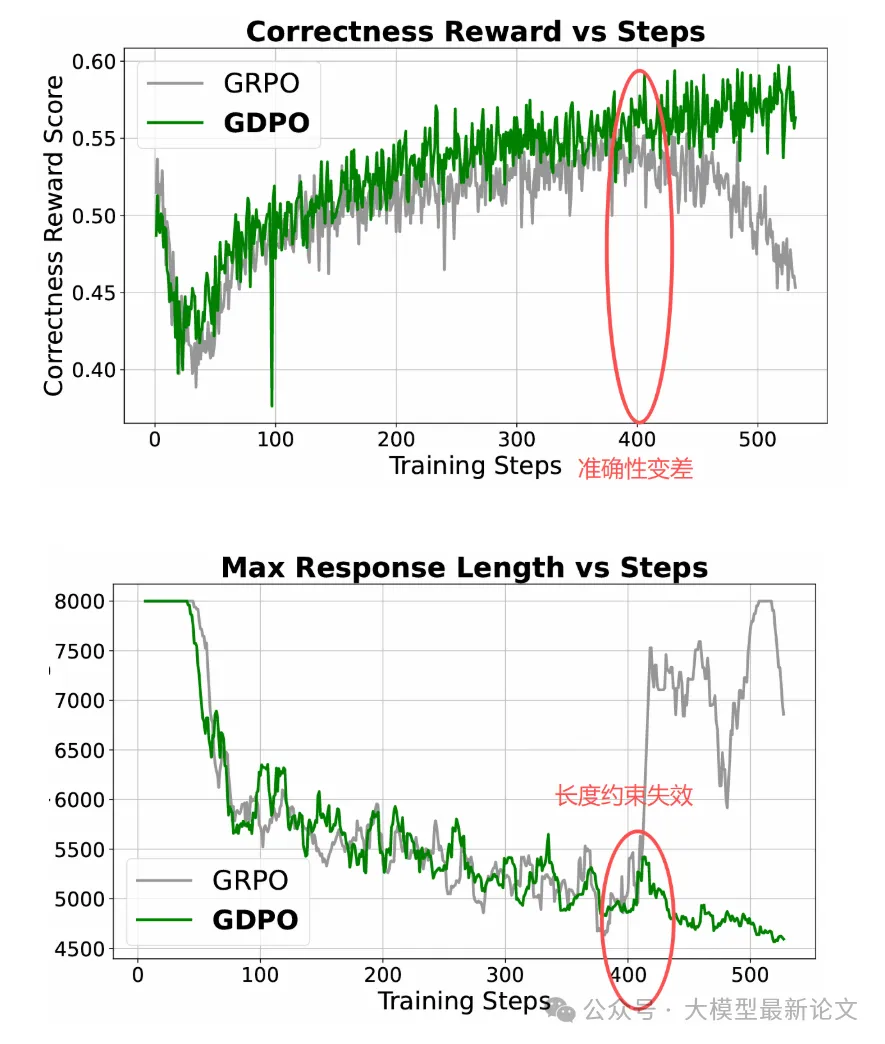
实验结论:
- 前100步:长度约束目标很容易,两个模型都很快掌握
- 100-400步:GDPO 的正确性恢复更快,达到更高值
- 400步后:GRPO 出现训练崩溃:
- 正确性奖励开始下降
- 长度约束直接失效
- 最难的 AIME 任务上,GDPO 优势最明显(+6.3% vs GRPO)
在数学任务设置上,作者分析了奖励加权的效果:
- 固定正确性权重 w_correct = 1.0
- 长度权重 w_length 在 {1.0, 0.75, 0.5, 0.25} 变化
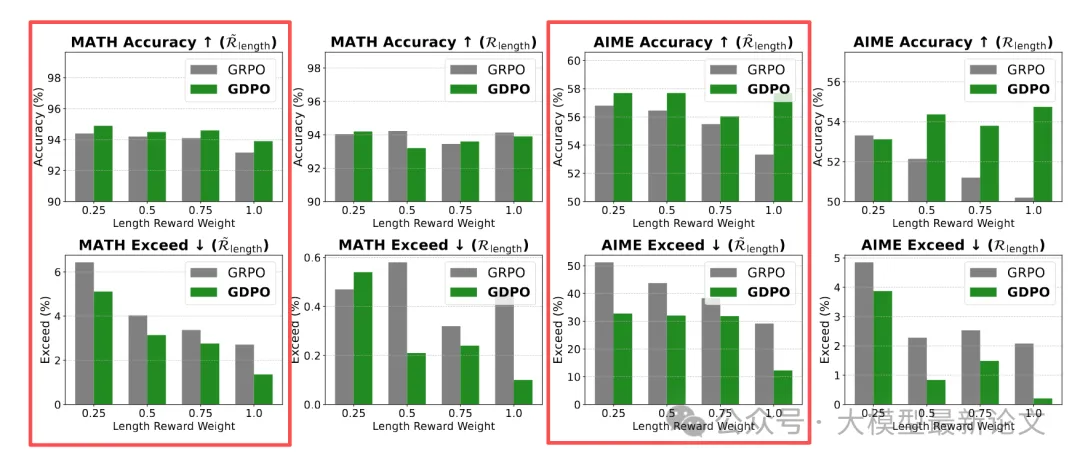
上图展示了标准 GRPO 与 GDPO 在使用上述不同奖励权重组合的情况下,准确率与超长率(回答长度超过限制)变化情况,其中红框中的是使用条件化长度奖励的结果,可见:
- w_length 从 1.0 降到 0.5,超长率几乎不变
- 只有降到 0.25(极端的 4:1 权重比),才能抵消两个目标的难度差异
这说明简单目标(长度)的"吸引力"太强,小幅调权重根本压不住。而对简单目标施加条件化约束后,问题得到解决,权重真正生效
任务3:代码推理(Code Reasoning)
在具有三项约束(准确率、长度约束、缺陷率)的代码推理场景上,GDPO 在多个维度上都优于 GRPO