REAP the Experts:为什么一刀切的 MoE 压缩里,Pruning 比 Merging 更稳、更准
这篇论文解决什么问题
Sparsely-activated Mixture-of-Experts(SMoE)在 LLM 里很香:预训练省算力、推理低延迟,但代价是 参数量爆炸 和 显存占用高 。于是大家开始做专家压缩。过去的结论常常是:在多选题(MC)上,Merging 比 Pruning 好。但这篇论文指出:一旦任务变成 生成式(code、math、creative writing、tool calling) ,结论会反过来,Pruning 更优,并且给出理论原因与新的剪枝准则 REAP。
关键结论一:Merging 会导致"功能子空间坍缩"
作者先建立一个极简但关键的分析:把两个专家 f i , f j f_i, f_j fi,fj 压成一个专家时,会发生什么?
原始 SMoE 层输出:
h ( x ) = ∑ k = 1 K g k ( x ) f k ( x ) h(x)=\sum_{k=1}^K g_k(x) f_k(x) h(x)=k=1∑Kgk(x)fk(x)
Merging 的根本问题
合并时把 g i ( x ) g_i(x) gi(x) 和 g j ( x ) g_j(x) gj(x) 直接相加,并用一个固定组合的专家 f ~ \tilde f f~ 替代:
h ~ ( x ) = ∑ k ≠ i , j g k ( x ) f k ( x ) + ( g i ( x ) + g j ( x ) ) f ~ ( x ) \tilde h(x) = \sum_{k\neq i,j} g_k(x)f_k(x) + \big(g_i(x)+g_j(x)\big)\tilde f(x) h~(x)=k=i,j∑gk(x)fk(x)+(gi(x)+gj(x))f~(x)
但原本两个专家在不同输入下的比例是动态的。定义:
r ( x ) = g i ( x ) g i ( x ) + g j ( x ) r(x) = \frac{g_i(x)}{g_i(x)+g_j(x)} r(x)=gi(x)+gj(x)gi(x)
原始组合实际上是:
( g i + g j ) ⋅ ( r ( x ) f i ( x ) + ( 1 − r ( x ) ) f j ( x ) ) (g_i+g_j)\cdot\Big(r(x)f_i(x)+(1-r(x))f_j(x)\Big) (gi+gj)⋅(r(x)fi(x)+(1−r(x))fj(x))
问题:Merging 强行把动态混合变成静态混合,理论上会引入不可消除的误差。
核心下界(论文定理):
Error = E [ ( g i + g j ) 2 ] ⋅ V a r [ r ( x ) ] ⋅ ∥ f i − f j ∥ 2 \text{Error} = \mathbb{E}\!\left[(g_i{+}g_j)^2\right]\cdot \mathrm{Var}[r(x)] \cdot \|f_i-f_j\|^2 Error=E[(gi+gj)2]⋅Var[r(x)]⋅∥fi−fj∥2
只要:
- router 的 mixing policy 不是常数( V a r [ r ] > 0 \mathrm{Var}[r]>0 Var[r]>0)
- 两专家不是同一个函数( ∥ f i − f j ∥ > 0 \|f_i-f_j\|>0 ∥fi−fj∥>0)
那么 误差必然 > 0。
Pruning 的优势
如果直接剪掉 f j f_j fj:
Error = E [ g j ( x ) 2 ∥ f i − f j ∥ 2 2 ] \text{Error} = \mathbb{E}[g_j(x)^2\|f_i-f_j\|_2^2] Error=E[gj(x)2∥fi−fj∥22]
这里没有 V a r [ r ] \mathrm{Var}[r] Var[r],所以 Pruning 不会因为策略多样性而受罚。这就是"功能子空间坍缩"结论的理论原因。
关键结论二:经验层面,Merging 在生成任务上崩得更快
作者用 PCA 可视化显示:在高层 MoE 中,Merging 会把专家输出子空间强行拉到中心,出现 "functional subspace collapse";Pruning 则保留原来的 manifold 结构。
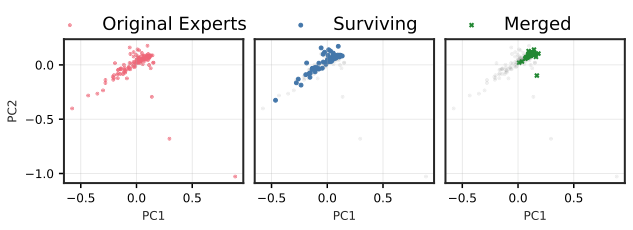
图解:Qwen3-30B 早期层 PCA 空间,Pruning 保留原分布形状,Merging 明显收缩。
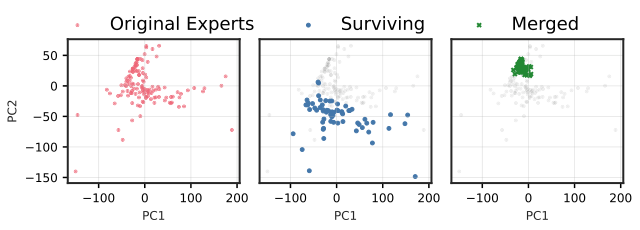
图解:Qwen3-30B 后期层 PCA 空间,Merging 收缩更剧烈,Pruning 仍保持原 manifold 结构。
REAP:Router-weighted Expert Activation Pruning
为了让 Pruning 更稳,作者提出新的剪枝准则 REAP ,直觉是:专家重要性不仅取决于 路由频率 ,还取决于 输出幅度。
定义专家 j j j 的 saliency:
S j = 1 ∣ X j ∣ ∑ x ∈ X j g j ( x ) ⋅ ∥ f j ( x ) ∥ 2 S_j = \frac{1}{|\mathcal{X}j|}\sum{x\in\mathcal{X}_j} g_j(x)\cdot \|f_j(x)\|_2 Sj=∣Xj∣1x∈Xj∑gj(x)⋅∥fj(x)∥2
含义:
- g j ( x ) g_j(x) gj(x):router gate 值
- ∥ f j ( x ) ∥ 2 \|f_j(x)\|_2 ∥fj(x)∥2:专家输出激活幅度
- X j \mathcal{X}_j Xj:该专家被 TopK 激活的 token 集合
剪掉 S j S_j Sj 最小的专家,就能最大限度减小 layer 输出变化。
实验设置概览
- 模型规模:21B 到 1T
- 压缩比例:25% / 50%
- Baseline:Frequency, EAN, HC-SMoE, M-SMoE
- 任务:MC QA、Code、Math、Creative Writing、Tool Calling
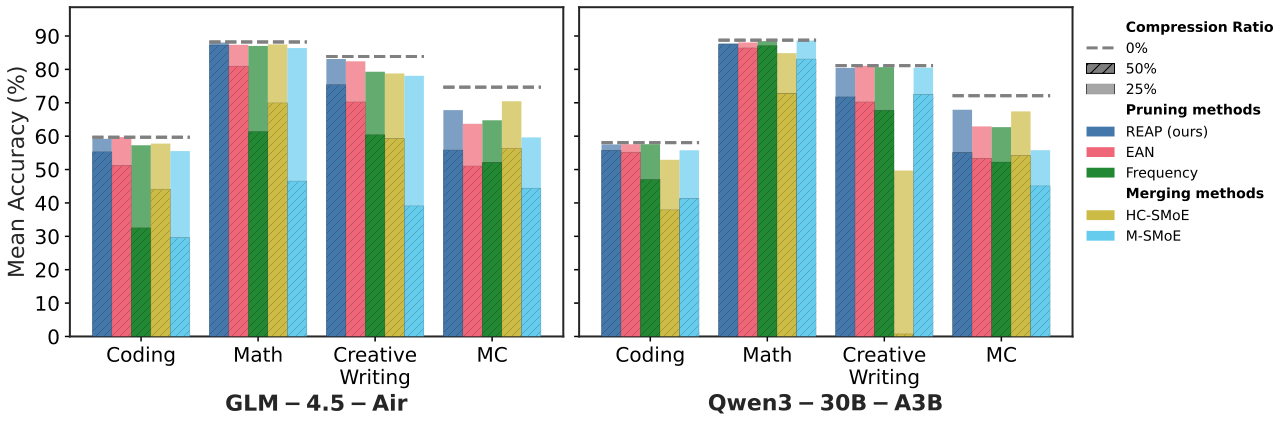
图解:GLM-4.5-Air 与 Qwen3-30B 在多任务上的压缩效果。50% 压缩时,Merging 在生成类任务上明显下滑,REAP 保持最好稳定性。
生成任务分析:Merging 为什么更差
作者进一步统计生成输出分布差异:
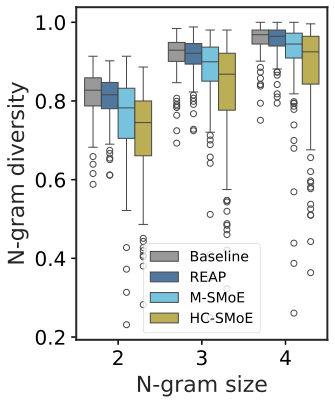
图解:N-gram 多样性。Merging 输出显著更重复,REAP 接近原模型。
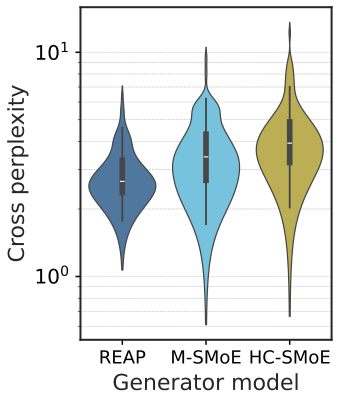
图解:cross perplexity,Merging 与原模型分布偏离更大。
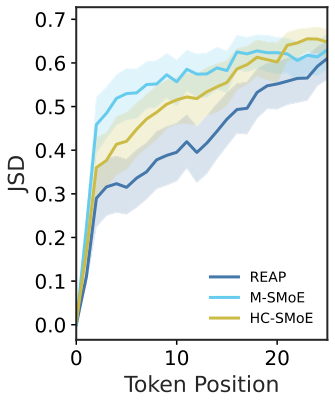
图解:logit JSD 随 token 位置变化。Merging 随序列增长快速失配,REAP 更稳。
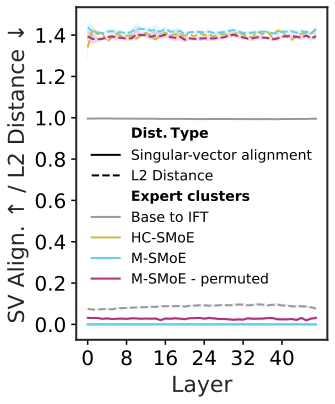
图解:专家权重间距离和奇异向量对齐度。专家之间差异大,导致 Merging 的"参数平均"本身就不稳定。
大模型级别验证
REAP 在 480B 和 1T 级别仍然稳定:
- Qwen3-Coder-480B:50% Pruning 仅 1.4% 代码准确下降
- Kimi-K2:50% Pruning 仍保持近无损表现
- 在 SWE-Bench、BFCLv3 等 agentic / tool tasks 上,REAP 依然稳于 Frequency 和 EAN
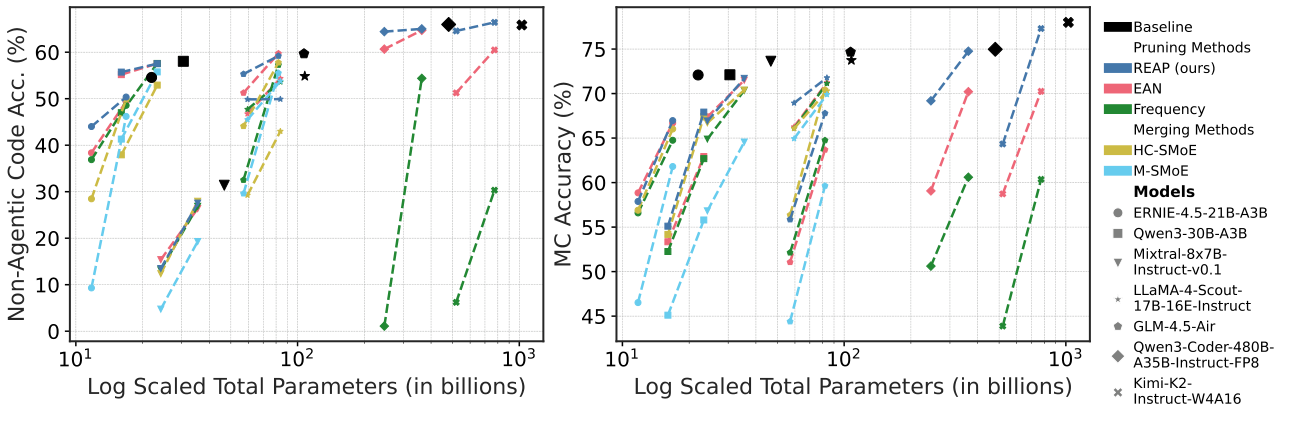
图解:Coding + MC vs 参数规模。50% 压缩时,REAP 显著优于其他方法。
Merging 的额外挑战:簇结构本身很糟
Merging 依赖聚类,但现实中聚类经常出现:
- 大量 singleton clusters
- 少量 mega-clusters(几十专家强行合并)
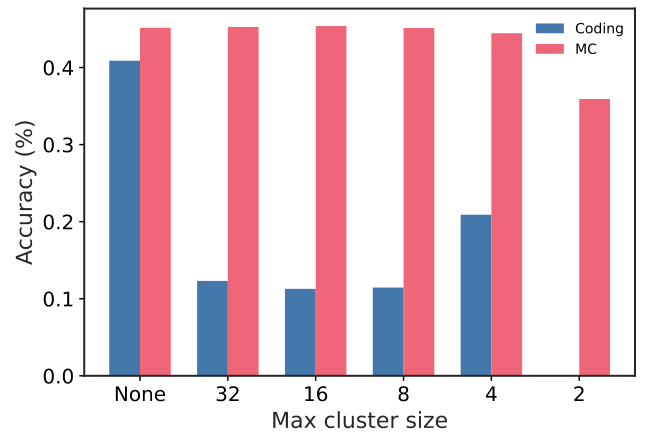
图解:限制最大 cluster size 后,编码任务准确率大幅下降,说明大簇是性能崩溃来源。
校准数据的重要性
生成任务必须用 领域数据校准,否则压缩模型可能完全失效。
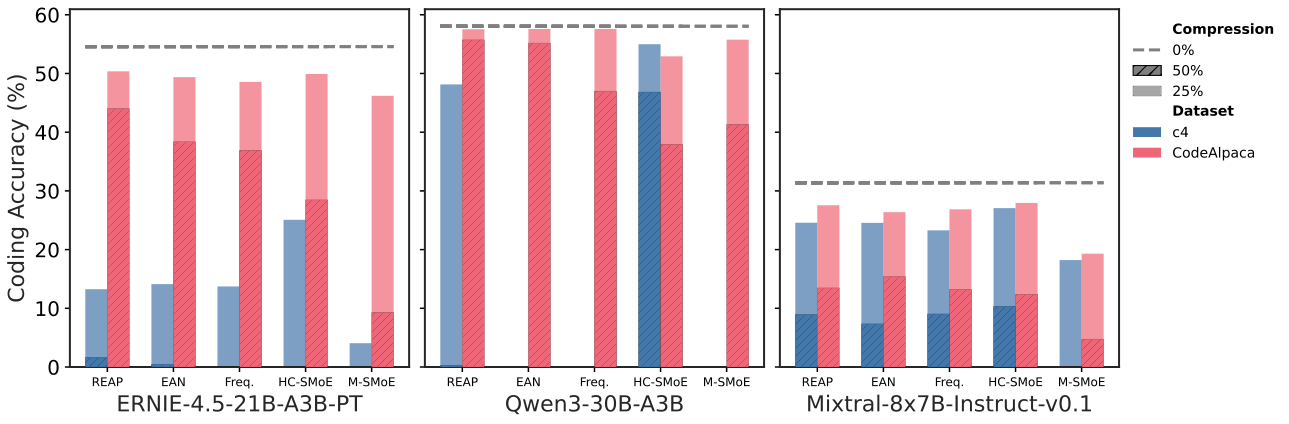
图解:用 c4 校准导致 coding 质量崩溃,领域数据明显更稳。
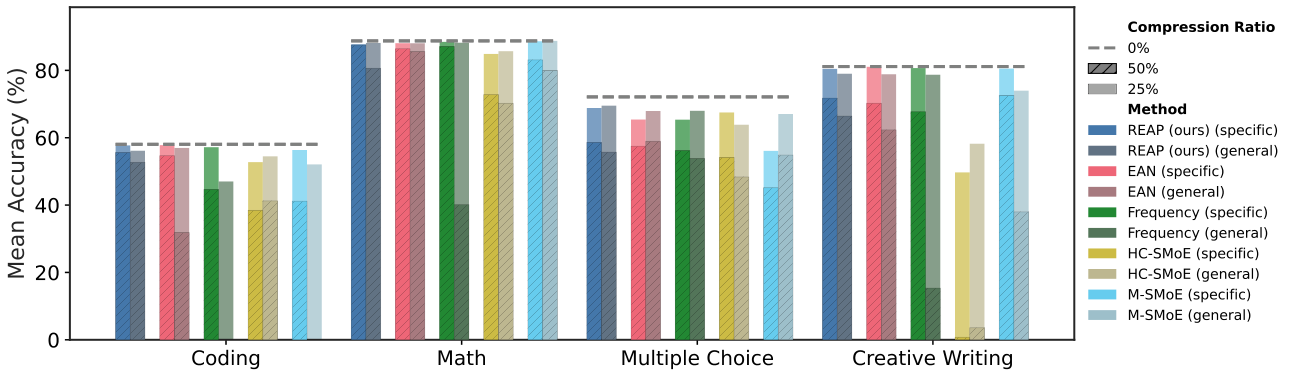
图解:领域校准在 50% 压缩下更关键,通用校准数据表现显著下降。
结论与意义
- Merging 在生成任务上存在不可消除的理论误差,根因是 router 控制权被绑定。
- Pruning 保留 router 独立控制,避免功能子空间坍缩。
- REAP 通过结合 gate 值与激活幅度,显著优于频率剪枝与 EAN,且能扩展到超大模型。
- 这篇论文说明:压缩 SMoE 时,只看 MC 或 perplexity 是误导性的,生成任务才是现实表现的关键。
本文参考自 REAP the Experts: Why Pruning Prevails for One-Shot MoE compression