文章目录
- [1. 推荐系统](#1. 推荐系统)
-
- [1.1 推荐的类型](#1.1 推荐的类型)
- [1.2 用数学语言表达](#1.2 用数学语言表达)
-
- [1.2.1 效用函数](#1.2.1 效用函数)
- [1.2.2 推荐系统的问题](#1.2.2 推荐系统的问题)
- [2. 基于内容的推荐系统(Content-Based Recommender Systems)](#2. 基于内容的推荐系统(Content-Based Recommender Systems))
-
- [2.1 Item Profile(物品画像)](#2.1 Item Profile(物品画像))
-
- [2.1.1 TF-IDF](#2.1.1 TF-IDF)
- [2.2 User Profiles(用户画像)](#2.2 User Profiles(用户画像))
-
- [2.2.1 例1](#2.2.1 例1)
- [2.2.2 例2](#2.2.2 例2)
- [2.3 如何确定是否喜欢](#2.3 如何确定是否喜欢)
- [2.4 优点](#2.4 优点)
- [2.5 缺点](#2.5 缺点)
- [3. 协同过滤(Collaborative Filtering)](#3. 协同过滤(Collaborative Filtering))
-
- [3.1 用户相似度](#3.1 用户相似度)
-
- [3.1.1 Jaccard相似度](#3.1.1 Jaccard相似度)
- [3.1.2 余弦相似度(Cosine Similarity)](#3.1.2 余弦相似度(Cosine Similarity))
- [3.1.3 中心化余弦相似度(Centered Cosine Similarity)](#3.1.3 中心化余弦相似度(Centered Cosine Similarity))
- [3.2 评分预测](#3.2 评分预测)
- [3.3 基于物品的协同过滤(Item--Item Collaborative Filtering)](#3.3 基于物品的协同过滤(Item–Item Collaborative Filtering))
-
- [3.3.1 示例](#3.3.1 示例)
- [3.4 优点](#3.4 优点)
- [3.5 缺点](#3.5 缺点)
- [3.6 混合推荐方法(Hybrid Methods)](#3.6 混合推荐方法(Hybrid Methods))
- [4. 评估推荐系统](#4. 评估推荐系统)
1. 推荐系统
推荐系统是在大量 items(商品/内容) 中,给用户推荐可能感兴趣的东西。
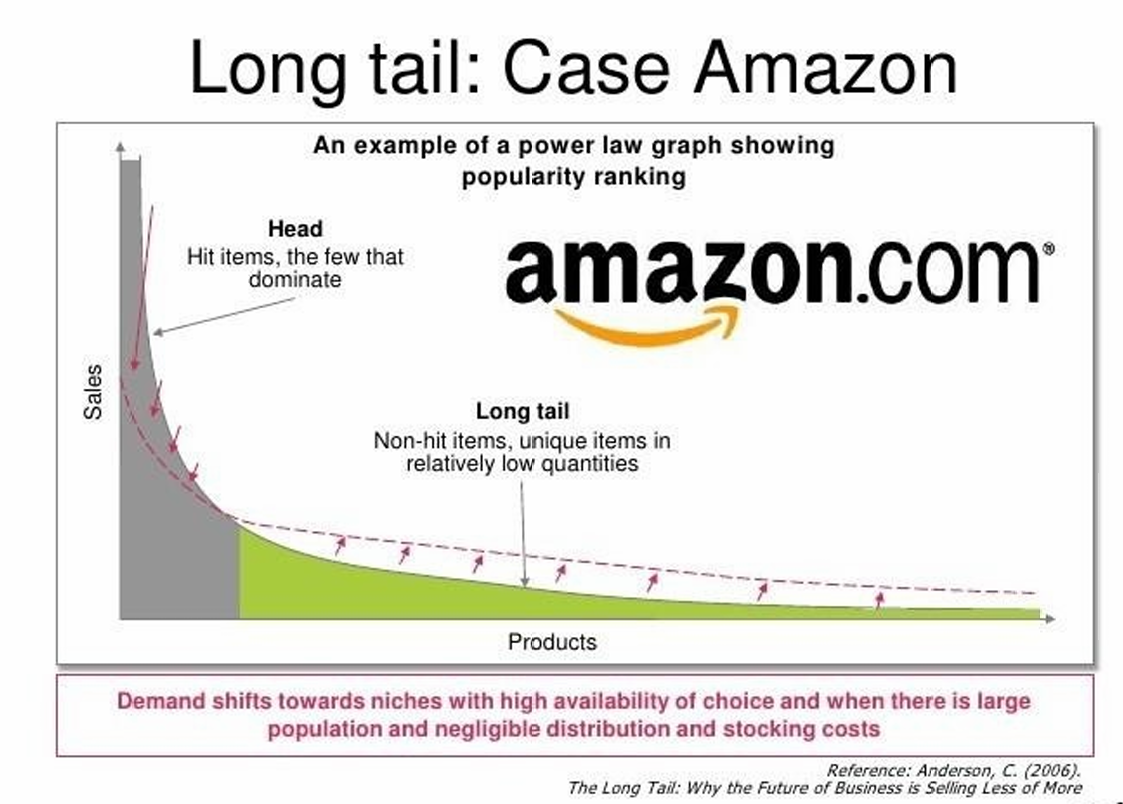
互联网的出现让信息传播成本几乎为0,这解决了过去资源稀缺的问题,但是带来了信息过剩,导致Long Tail(长尾效应)。
长尾效应指的是少数热门内容(头部)大量冷门内容(长尾),而长尾加起来的价值非常大。而Amazon、Netflix 能靠卖"冷门但很多"的东西赚钱
因此选择越多,因此就越需要推荐引擎来做过滤。
或者说推荐系统是在用户没有明确搜索时,主动从海量内容中筛选并推送"可能感兴趣的东西"。
1.1 推荐的类型
有三种类型的推荐:
- 人工编辑 / 人工精选推荐。
这是完全靠人来选,不需要算法。
例子有:编辑精选、必买清单、年度最佳、收藏列表。 - 简单统计型推荐
这是对所有用户一视同仁,只做统计排序。
例如: 最受欢迎、销售前10、最新上架。 - 为"每个用户"量身定制的推荐(Tailored to individual users)
这是根据用户历史、行为、偏好给不同用户推不同内容。
这是我们这部分要说的,也是市面上Amazon、Netflix、TikTok所使用的推荐。
1.2 用数学语言表达
X X X表示所有用户的集合。
S S S表示所有物品的集合。
u : X × S → R u:X×S→R u:X×S→R是效用函数。
它是给定一个用户 X X X和一个物品 S S S,
返回一个数值,表示用户有多喜欢这个物品。
R R R是评分空间,存放"喜欢程度"的数值,是一个可以比较大小的集合(全序)。
例子:是 0--5 星或 0--1 之间的实数。
1.2.1 效用函数
下面的表格展示了效用矩阵(Utility Matrix) / 用户--物品评分矩阵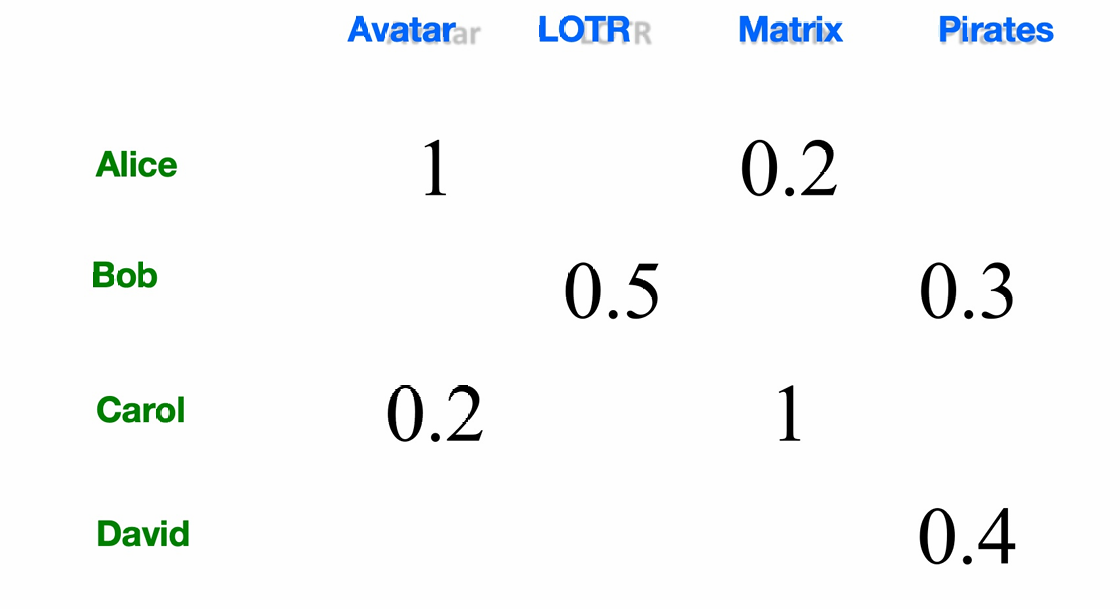
这里单元格里的数字,表示这个用户有多喜欢这部电影。
Alice 对 Avatar 的评分是 1 → 非常喜欢
Alice 对 Matrix 的评分是 0.2 → 不太喜欢
Bob 对 LOTR 的评分是 0.5 → 一般
Carol 对 Matrix 的评分是 1 → 非常喜欢
David 对 Pirates 的评分是 0.4 → 一般
需要注意的是这里的空白表示未知(没看过/没评分),而非不喜欢。
大多数用户只看过极少数物品,所以 utility matrix 是 高度稀疏(sparse) 的。
1.2.2 推荐系统的问题
由刚刚的效用矩阵(Utility Matrix),我们得到了推荐系统要解决的三大核心问题。
- 如何得到"已知的评分"(Gathering "known" ratings for matrix)
我们如何手机Utility Matrix里的数据。一般分显式(用户主动打分或者直接问用户,但是现实中鲜果不好,因为用户不愿意被打扰)和隐式(从行为推断喜好,例如购买代表可能喜欢,但是没买不是代表不喜欢,可能是没看到、没买、没点等等)。 - 用已知评分,推断未知评分(Extrapolate unknown ratings from the known ones)
重点不是"你讨厌什么",而是我们只关心你可能会"很喜欢"的那些未知项。
因为推荐是为了 推你可能喜欢的东西。不需要精确预测所有低分。
这个问题的难点在于效用矩阵是稀疏的(sparse)。
这就涉及到了Cold start(冷启动问题):
新物品:没人评过分,系统不知道该推荐给谁。
新用户:没历史行为,系统不知道他喜欢什么。
三种推荐系统思路(重点框架):
Content-based(基于内容)、Collaborative(协同过滤)、Latent factor based(隐因子)。这章后续将介绍前两种。
第一种是看物品本身的特征,给你推荐"和你以前喜欢的东西相似的"。第二种是看和你相似的人,"你和他们喜欢的一样"。第三种是用矩阵分解(PCA/SVD),自动学"潜在兴趣维度"。 - 怎么评估推荐算法好不好(Evaluating extrapolation methods)
问题是:预测准不准?推荐有没有用?
常见评估:预测误差(RMSE 等);推荐效果(命中率、排序)。
2. 基于内容的推荐系统(Content-Based Recommender Systems)
核心思想:给用户 x x x推荐的东西,应当和他过去"高分喜欢过"的东西在内容上相似。
这里的content指的是物体本身的特征,不是评分本身而是例如电影:演员、导演、类型、关键词。
新闻/网页:文本内容、主题词、标签。
因此如果你喜欢科幻,喜欢某个导演,或者给某些电影打了高分。那么系统就会推荐同演员 / 同导演 / 同类型 的电影。
再比如经常看 AI / 科技文章,那么系统就会推荐 AI / 科技 网站、博客、新闻。
下图介绍了一个基于内容的推荐系统。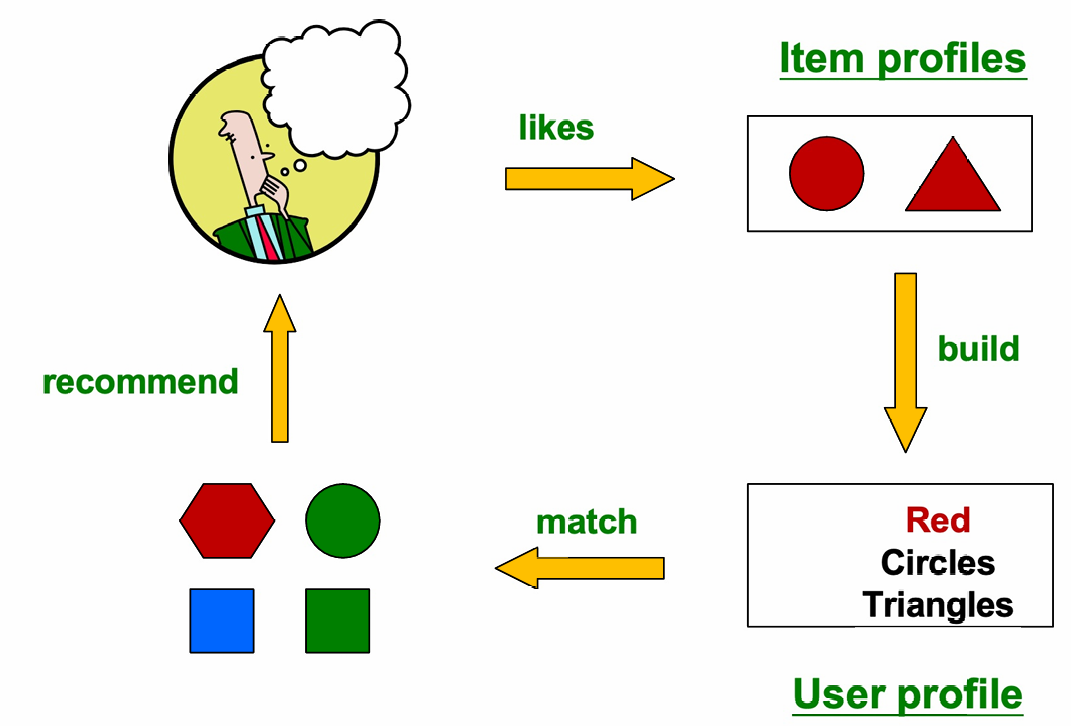
用户喜欢右上角这样的一些 item,所以系统就根据这些 Item profiles 做聚合,从而得到了 User profile,比如这里系统认为用户偏好红色、圆形、三角形。因此系统就会按照这个 User profile 去所有候选物品中做相似度计算从而找到最像用户感兴趣的物品推荐给用户。
2.1 Item Profile(物品画像)
当然对于这里的操作我们需要将每个物品变成一个向量。因此对每一个物品,都要建一个 item profile,我们用一个统一的方式表示从而方便后面进行相似度计算。
因此 Item profile 本质是一个"特征向量",即 p r o f i l e = [ f e a t u r e 1 , f e a t u r e 2 , . . . , f e a t u r e n ] profile = [feature_1, feature_2, ..., feature_n] profile=[feature1,feature2,...,featuren]。
不同类型的 item,特征不同。
例如电影的特征包括作者、演员、导演、类型(genre)。
文本的特征包含一些文档里重要的词,当然也包含每个词。
那怎么选"重要特征"呢?
这里经常使用文本挖掘(text mining)的经典方法------TF-IDF。
TF-IDF = Term Frequency × Inverse Document Frequency
TF:这个词在当前文档里出现得多不多。
IDF:这个词在所有文档里是不是"太常见"。
IDF可以帮助我们将常见废词(the/is)降低,从而将更有意义的内容保留下来。
所以在推荐系统里,文本里的 词 = 特征,文本本身 = 一个 item。
2.1.1 TF-IDF
正如前面所说,我们希望文本的特征包含一些文档里重要的词,所以TF-IDF的目标就是给重要且有区分度的词以更高的权重,而给到处都有的废词更低权重。
T F i j = f i j max k f k j TF_{ij} = \frac{f_{ij}}{\max_k f_{kj}} TFij=maxkfkjfij,这是对词频做归一化,用于消除文档长度差异。
其中 f i j f_{ij} fij:词(feature) i i i 在文档(item) j j j 中出现的次数。
在越少文档中出现的词,IDF 越大,区分度越高。
I D F i = log ( N n i ) IDF_i = \log\left(\frac{N}{n_i}\right) IDFi=log(niN)
其中 n i n_i ni:包含词 i i i的文档数量。
N N N:文档总数。
TF-IDF 权重(最终分数)为:
w i j = T F i j × I D F i w_{ij} = TF_{ij} \times IDF_i wij=TFij×IDFi
用一句话概况那就是在这篇文档里常见,但在整体里少见的词,权重最高。
因此对于文本, Doc profile = TF-IDF 分数最高的一组词 + 它们的权重。
也就是选 TF-IDF 最大的几个词,把它们当作这个 item 的特征向量。
2.2 User Profiles(用户画像)
用户画像的构建方式有很多:
- 最基础、常用的方法是对于用户的 item profile向量的评分作为权重从而做加权平均。
- 改进版:用"用户平均评分"做归一化。
有的人打分偏高(什么都 4--5 分),而有的人打分很严格(很少给高分)。为了解决这个问题,我们可以先减去用户的平均评分,再用"相对喜好"当权重。所以用户的5分现在这指的是比他平常打得高。 - 更复杂的方法也可以。
2.2.1 例1
我们用一个布尔型效用矩阵演示 user profiles 如何从 item profiles 算出来。
Items 是电影,唯一特征是"演员"。
每个演员是一个特征维度。
如果电影有这个演员 → 1,没有 → 0。
举例(假设只有演员 A 和 B):
电影 1(有 A): [ 1 , 0 ] [1, 0] [1,0]。
电影 2(有 B): [ 0 , 1 ] [0, 1] [0,1]。
用户 x x x看过 5 部电影:2 部有演员 A,3 部有演员 B。
因为是 boolean,每个 item profile 是 0/1,直接取平均就是"比例"。
Feature A 权重: 2 5 = 0.4 \frac{2}{5} = 0.4 52=0.4
Feature B 权重: 3 5 = 0.6 \frac{3}{5} = 0.6 53=0.6
因此 user profiles 是 u x = [ 0.4 , 0.6 ] u_x=[0.4, 0.6] ux=[0.4,0.6]
表示演员喜欢演员 A 和 B,但是更偏好 B。
2.2.2 例2
我们刚刚是布尔型,我们现在改成连续的带星级评分的用户画像。
例子与刚刚一直,但是有 1-5 星评分。
Actor A 的电影评分:3、5。
Actor B 的电影评分:1、2、4。
这里需要做一个关键操作,对这里的分数进行归一化操作。
这里的所有评分是: 3、5、1、2、4。 所以平均值是3。
因此对于演员 A 的电影评分,归一化的结果就是 0 和 +2。
因此取平均的结果就是 1。
表示:演员 A 明显高于用户平均偏好。
而对于演员 B 的电影评分,归一化的结果是 -2 ,-1和 +1。
因此取平均的结果就是 − 2 3 -\frac{2}{3} −32。
表示:演员 B 整体低于用户平均偏好。
因此 user profiles 是 u x = [ 1 , − 2 3 ] u_x=[1, -\frac{2}{3}] ux=[1,−32]
表示用户 更喜欢演员 A,对演员 B 整体不太感兴趣。
2.3 如何确定是否喜欢
那么对于 Content-Based Recommender Systems,系统怎么最终打分 / 预测给定一个用户和一个物品,他是否会喜欢呢?
这里使用余弦相似度(cosine similarity)进行计算。
u ( x , i ) = cos ( x , i ) = x ⋅ i ∥ x ∥ ∥ i ∥ u(x,i) = \cos(\mathbf{x}, \mathbf{i}) = \frac{\mathbf{x} \cdot \mathbf{i}} {\lVert \mathbf{x} \rVert \, \lVert \mathbf{i} \rVert} u(x,i)=cos(x,i)=∥x∥∥i∥x⋅i,
其中 x \mathbf{x} x:用户画像向量(user profile)。
i \mathbf{i} i:物品画像向量(item profile)。
x ⋅ i \mathbf{x} \cdot \mathbf{i} x⋅i:点积。
∥ x ∥ 、 ∥ i ∥ \lVert \mathbf{x} \rVert、\lVert \mathbf{i} \rVert ∥x∥、∥i∥:向量长度(范数)
如下图所示。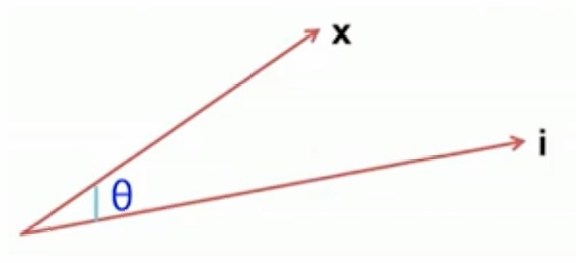
θ θ θ 小 → c o s cos cos 接近 1 → 非常相似
𝜃 = 90 ∘ 𝜃=90^∘ 𝜃=90∘→ c o s = 0 cos = 0 cos=0 → 无关
𝜃 > 90 ∘ 𝜃>90^∘ 𝜃>90∘→ c o s < 0 cos < 0 cos<0 → 偏好相反
2.4 优点
基于内容推荐的优点如下:
- 不需要其他用户的数据(No need for data on other users)
不存在 cold-start 和稀疏性问题,也就是新物品只要有内容就立马能被推荐而不需要等待第一个人来评分。 - 能服务"口味很小众"的用户(Able to recommend to users with unique tastes)
- 能推荐新内容 / 冷门内容(Able to recommend new & unpopular items)
同样不需要等待第一个人来评分。 - 推荐结果"可解释"(Able to provide explanations)
因为推荐是基于内容特征匹配。
2.5 缺点
基于内容推荐的缺点如下:
- 选对"内容特征"本身就很难(Finding the appropriate features is hard)
文本可以使用 TF-IDE,但是对于图片、电影、音乐这种包含情绪、风格、美感的很难用简单特征表示。 - 过度专一(Overspecialization)
系统只推荐"你已经喜欢的那一小块东西"。因此不会推荐用户内容画像以外的东西。但是用户可能有多种兴趣。这样无法利用其他用户的质量评价(Unable to exploit quality judgments of other users)。 - 新用户问题(Recommendations for new users)
Content-based 仍然无法解决新用户冷启动问题,因为没有历史,就没有 user profiles。
3. 协同过滤(Collaborative Filtering)
核心思想:和你兴趣相似的人,喜欢的东西,你也很可能喜欢。
我们要给用户 x x x做推荐。
首先找一组和 x x x评分"相似"的其他用户 N N N。这些用户被称为邻居(neighbors)。
用邻居用户的评分来预测 x x x的评分。
下图同样展示了这个过程。
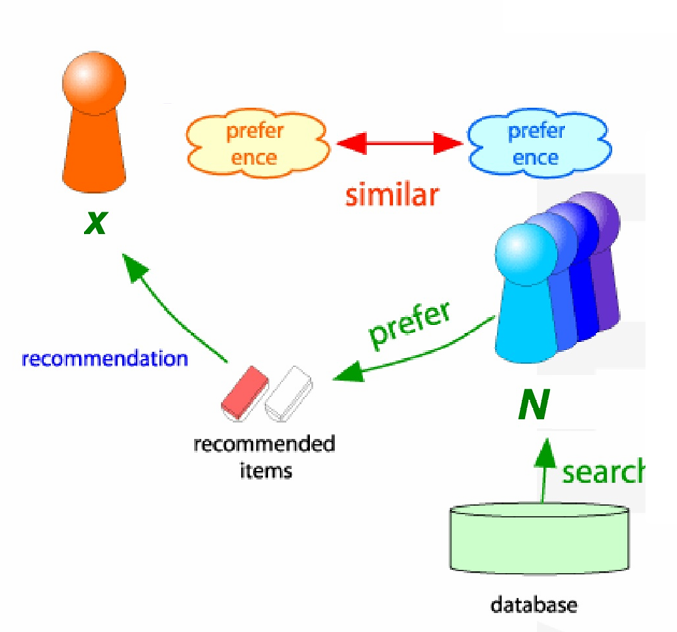
我们有用户 x x x,找到一群和他 preference(偏好)相似 的用户 N N N,这些用户在数据库里喜欢了一些物品。把这些物品推荐给 x x x。
3.1 用户相似度
我们该如何判断用户是否相似呢?
下图展示了一个评分矩阵。

我们现在要找到一群和目标用户评分模式相似的用户。
我们可以对每个用户:将用户对所有物品的评分当成一个向量 r x = ( r x 1 , r x 2 , . . . ) r_x=(r_{x1},r_{x2},...) rx=(rx1,rx2,...)。
我们需要一个函数用于计算相似度: s i m ( x , y ) sim(x,y) sim(x,y)。
我们希望这个公式符合人类直觉:如果两个用户给同一批电影打了相近的分,那么他们就很相似。同样如果 s i m ( A , B ) > s i m ( A , C ) sim(A,B)>sim(A,C) sim(A,B)>sim(A,C),那么A和B重合部分比A和C高。
3.1.1 Jaccard相似度
我们尝试使用 Jaccard 相似度。
计算式方式是计算 A 和 B 的交集个数以及并集个数,从而计算比值。
公式为: s i m ( A , B ) = ∣ r A ∩ r B ∣ ∣ r A ∪ r B ∣ \mathrm{sim}(A,B) = \frac{\lvert r_A \cap r_B \rvert} {\lvert r_A \cup r_B \rvert} sim(A,B)=∣rA∪rB∣∣rA∩rB∣
回到上面的例子,那么 A 和 B 的相似度为 s i m ( A , B ) = 1 5 \mathrm{sim}(A,B) = \frac{1}{5} sim(A,B)=51
A 和 C 的相似度为 s i m ( A , C ) = 2 4 \mathrm{sim}(A,C) = \frac{2}{4} sim(A,C)=42
因此 s i m ( A , B ) < s i m ( A , C ) sim(A,B)<sim(A,C) sim(A,B)<sim(A,C)
这么做虽然可以快速计算,但是忽略了评分。比如这里A和B其实都对HP1打了高分,说明他们都喜欢HP1,而A和C对TW和SW1的评价完全不同,因此应该是A和C喜好不一致而A和B喜好一致,因此应该是 s i m ( A , B ) > s i m ( A , C ) sim(A,B)>sim(A,C) sim(A,B)>sim(A,C),但是这里得出的结论违背了我们的直觉。
3.1.2 余弦相似度(Cosine Similarity)
因此我们介绍刚刚也使用过的余弦相似度。通过评分向量的方向相似度去判断。
公式为 s i m ( x , y ) = cos ( r x , r y ) = ∑ i r x i r y i ∑ i r x i 2 ∑ i r y i 2 \mathrm{sim}(x,y) = \cos(\mathbf{r}x, \mathbf{r}y) = \frac{\sum_i r{x i}\, r{y i}} {\sqrt{\sum_i r_{x i}^2}\; \sqrt{\sum_i r_{y i}^2}} sim(x,y)=cos(rx,ry)=∑irxi2 ∑iryi2 ∑irxiryi
s i m ( A , B ) = cos ( r A , r B ) \mathrm{sim}(A,B) = \cos(\mathbf{r}_A, \mathbf{r}_B) sim(A,B)=cos(rA,rB)
这里分子表示两个人在同一部电影上的评分重合程度,
分母表示各自评分"强度"的归一化,
结果表示只看方向是否一致,不看绝对大小。
根据前面的例子,我们可以得到 s i m ( A , B ) = 0.38 sim(A,B)=0.38 sim(A,B)=0.38
s i m ( A , C ) = 0.32 sim(A,C)=0.32 sim(A,C)=0.32
所以 s i m ( A , B ) > s i m ( A , C ) sim(A,B)>sim(A,C) sim(A,B)>sim(A,C),但差距不大。
但这个方法也存在问题:在计算中,没评分 = 0,0 也会参与点积和范数计算。没评分可能只是没看到、没时间、没机会。但 cosine similarity 会:
把大量"空白"当作负信号,拉低相似度。
换句话说稀疏矩阵下效果会被严重扭曲。
3.1.3 中心化余弦相似度(Centered Cosine Similarity)
先把每个用户的评分减去他自己的平均评分(做中心化),再用 cosine similarity 计算用户相似度。
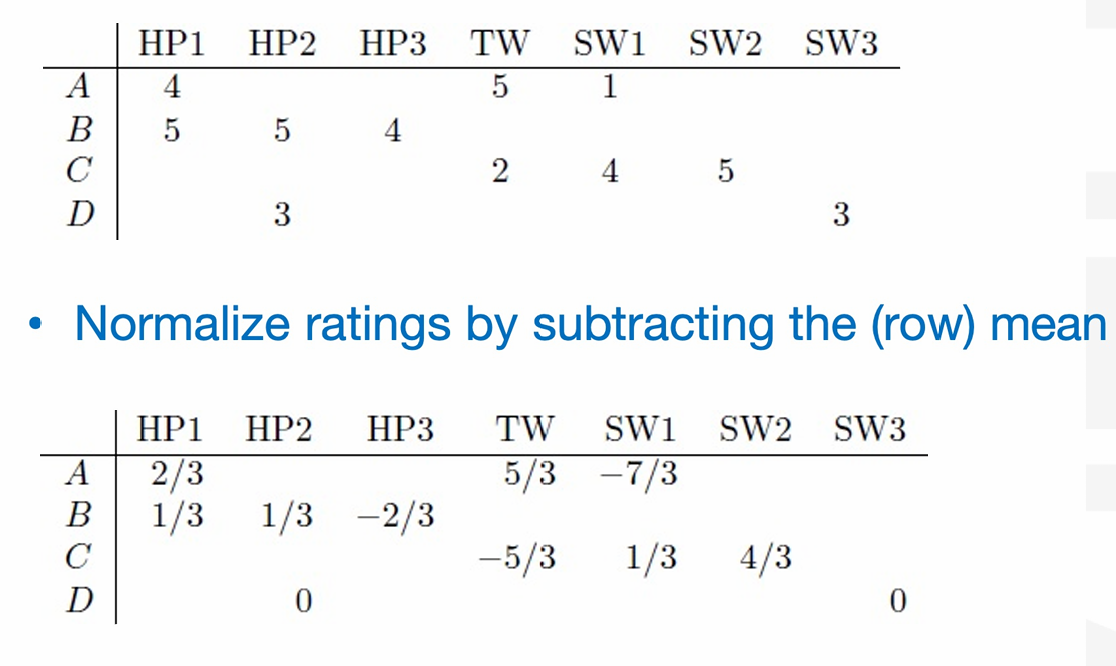
我们这样做还可以解决相似度被个人大份习惯干扰的问题。我们得出来的新评分中,正数表示比他平时更喜欢,负数表示比他平时更不喜欢,0表示一般。
我们对做完中心化后的向量,再做 cosine similarity。
得到的结果是 s i m ( A , B ) = 0.09 sim(A,B)=0.09 sim(A,B)=0.09
s i m ( A , C ) = − 0.56 sim(A,C)=-0.56 sim(A,C)=−0.56
所以 s i m ( A , B ) > s i m ( A , C ) sim(A,B)>sim(A,C) sim(A,B)>sim(A,C)。
现在这里的结果表示用户 A 和 B 在共同看过的电影上,大致方向一致。用户 A 和 C 偏好方向相反。所以 A 和 B 比 A 和 C 更"像"。
为什么这样的操作能够解决前面方案里 0 带来的问题呢?
因为这里的 0 是代表平均水平,所以是中性值,不像前面的 0 是会带来负面效果。换句话说 0 不会扣分。
平均化操作可以避免人们打分之间的松紧程度不一样。
s i m ( x , y ) = ∑ s ∈ S x y ( r x s − r ˉ x ) ( r y s − r ˉ y ) ∑ s ∈ S x y ( r x s − r ˉ x ) 2 ∑ s ∈ S x y ( r y s − r ˉ y ) 2 \mathrm{sim}(x,y) =\frac{ \sum_{s \in S_{xy}} (r_{xs} - \bar r_x)(r_{ys} - \bar r_y) }{ \sqrt{\sum_{s \in S_{xy}} (r_{xs} - \bar r_x)^2} \; \sqrt{\sum_{s \in S_{xy}} (r_{ys} - \bar r_y)^2}} sim(x,y)=∑s∈Sxy(rxs−rˉx)2 ∑s∈Sxy(rys−rˉy)2 ∑s∈Sxy(rxs−rˉx)(rys−rˉy)
其中 r ˉ x \bar r_x rˉx, r ˉ y \bar r_y rˉy是用户 x 、 y x、y x、y的平均评分, S x y S_{xy} Sxy是两人都评分过的项目集合。
这个公式同时也是 Pearson 相关系数(Pearson Correlation)
3.2 评分预测
现在我们知道哪些用户与该用户相似,那么我们如何根据这些相似用户的评分进行评分预测呢?
现在我们用用和用户 x x x最相似的一批用户 N N N(包含 k k k名用户),对某个物品 I I I的评分,来预测 x x x对 I I I的评分。
我们很容易想到直接将这些人的评分计算平均值:
r x i = 1 k ∑ y ∈ N r y i r_{xi}= \frac{1}{k} \sum_{y \in N} r_{yi} rxi=k1∑y∈Nryi
这么做其实没有区分非常像和有点像的用户,因为每个人的权重都一致。
因此我们有了一下的第二个公式:
r x i = ∑ y ∈ N s x y r y i ∑ y ∈ N s x y r_{xi}= \frac{\sum_{y \in N} s_{xy}\, r_{yi}} {\sum_{y \in N} s_{xy}} rxi=∑y∈Nsxy∑y∈Nsxyryi
这里的 s x y s_{xy} sxy是相似度 s x y = s i m ( x , y ) s_{xy} = \mathrm{sim}(x,y) sxy=sim(x,y)
相似度越高的用户,对预测的影响越大。
3.3 基于物品的协同过滤(Item--Item Collaborative Filtering)
我们其实可以将前面的操作对象换一下,我们不再找"和我相似的用户",而是找"和这个物品相似的其他物品"。然后用用户已经评价过的、与目标物品相似的物品,来预测评分。
我们前面是找与用户 x x x向此的用户 D D D,用这些用户对物品 I I I的评分预测 x x x对 I I I的评分。
现在是找和物品 I I I相似的物品,用用户 x x x对这些物品的评分来预测 x x x对 I I I的评分。
公式结构和 user--user 完全对称
r x i = ∑ y ∈ N ( i ; x ) s i j r x j ∑ y ∈ N ( i ; x ) s i j r_{xi}= \frac{\sum_{y \in N(i;x)} s_{ij}\, r_{xj}} {\sum_{y \in N(i;x)} s_{ij}} rxi=∑y∈N(i;x)sij∑y∈N(i;x)sijrxj
其中 r x i r_{xi} rxi是用户 x x x对物品 i i i的评分。
j j j是和物品 i i i相似的其他物品。
N ( i ; x ) N(i;x) N(i;x)是用户 x x x以及评分过的、且与 i i i相似的物品集合。
s i j s_{ij} sij是物品 i i i和物品 j j j的相似度。
r x j r_{xj} rxj是用户 x x x对物品 j j j的已知评分。
那这个和我们前面的基于内容的推荐系统根据用户喜欢的物品 item profiles 生成 user profiles,然后根据这个user profiles推荐有什么区别呢?
两者其实在预测阶段形式非常接近。都可以理解为我们根据用户喜欢的其他问题知道用户是否喜欢这类物体,如果这个新来的物体与之类似,那么我们就可以预测。
区分点在于这里是怎么得到类似的结论的。这里物体之间是否类似还是根据别的用户的评分是否类似来的,而前面基于内容的推荐系统的物品相似度是根据物品的内容特征来的。
因此就像前文所说,基于内容的推荐系统不需要其他用户的数据,而这里的基于物品的协同过滤会有冷启动问题。
3.3.1 示例
下图展示了一组数据。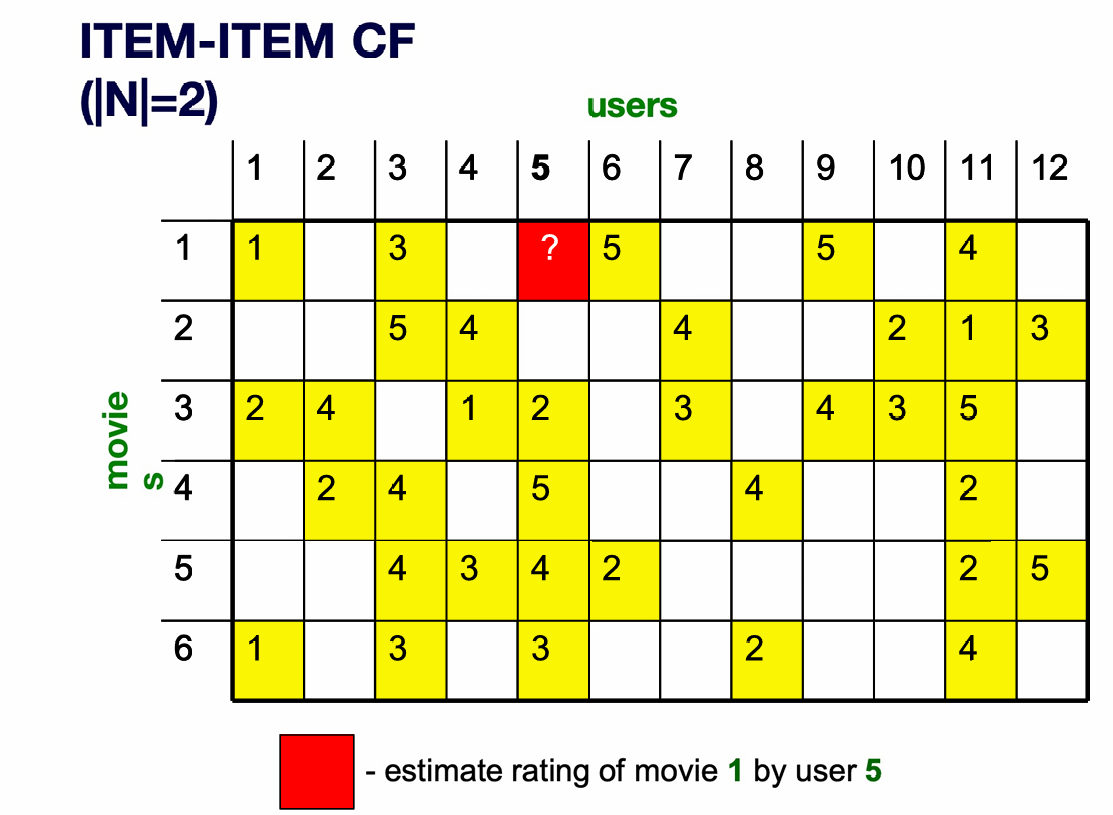
我们希望根据这些用户对这些电影的打分来预测用户5对电影1的打分。
我们的解决思路是找到和电影 1 最相似的、且用户 5 已经评分过的 2 部电影。
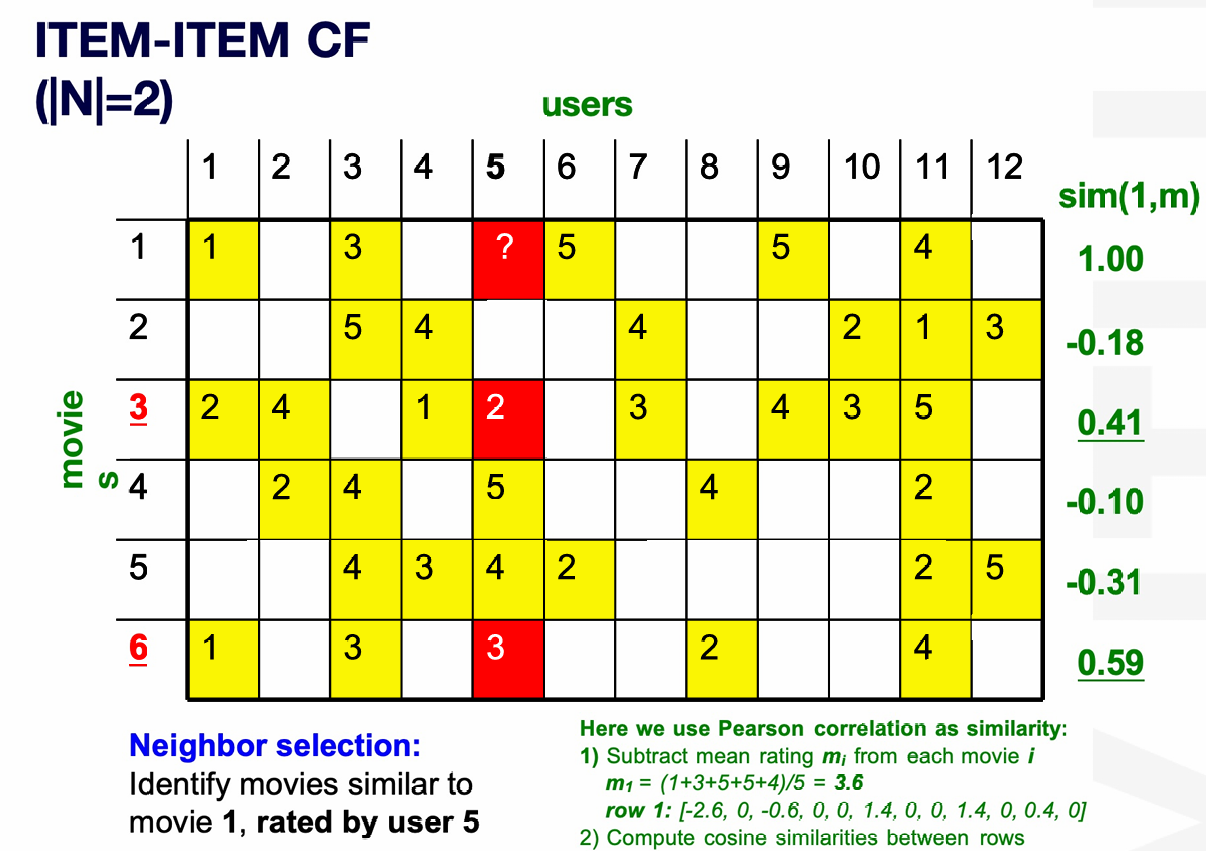
我们这里使用中心化余弦(Pearson correlation)计算电影1和其他电影的相似度。得出是电影3和电影6和电影1最相似,而且用户5给他们打过分。
因此我们现在可以预测用户 5 给电影 1 的评分为:
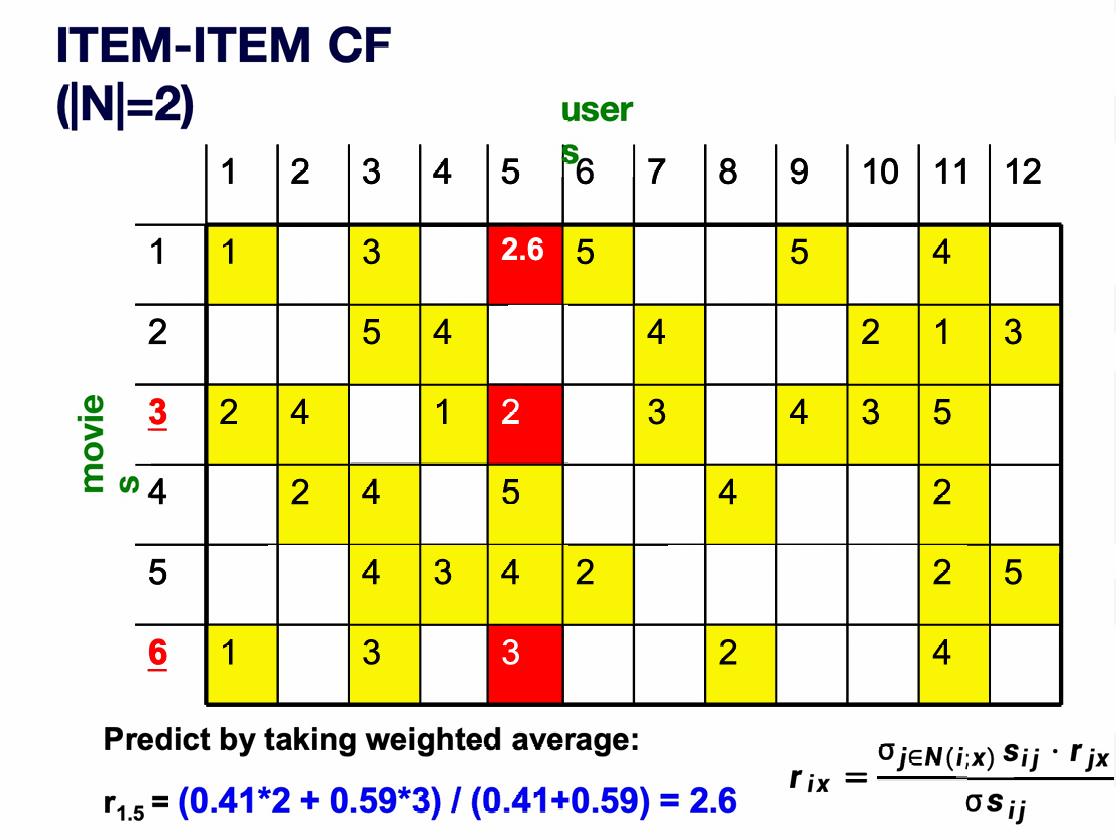
根据公式 r i x = ∑ j ∈ N ( i ; x ) s i j r j x ∑ j ∈ N ( i ; x ) s i j r_{ix}= \frac{\sum_{j \in N(i;x)} s_{ij} \, r_{jx}} {\sum_{j \in N(i;x)} s_{ij}} rix=∑j∈N(i;x)sij∑j∈N(i;x)sijrjx,
我们电影1和电影3的相似度是0.41,用户5给电影3的评分是2,电影1和电影6的相似度是0.59,用户5给电影6的评分是3,代入公式后计算结果为2.6。
在实际系统中,经验证明 Item--Item 协同过滤通常比 User--User 表现更好。

因为物品更"稳定",用户更"复杂"。电影《Matrix》就是《Matrix》,特征相对稳定。而用户同一个人可能每天都有不同的想法,口味是多模态的、会变化的。
3.4 优点
其的优点有:
- 适用于任何类型的物品(Works for any kind of item)。
不需要人为设计或提取物品特征。协同过滤只依赖用户行为(评分 / 点击 / 购买),不关心物品"是什么"。
而之前的内容推荐要有 item profile(actor / genre / keywords)。
3.5 缺点
其的缺点有:
- Cold Start(冷启动问题)
系统中需要"足够多的用户",才能找到相似对象。 - 稀疏性问题
用户--评分矩阵非常稀疏(大多数是空的),很难找到两个用户对"同一批物品"都打过分。 - 首评者问题(First rater problem)
如果一个物品从未被评分,协同过滤无法推荐。这对新物品、冷门物品(Esoteric items)尤其吃亏。 - 流行度偏置(Popularity bias)
难以服务"口味非常独特"的用户。系统更倾向推荐热门物品。
3.6 混合推荐方法(Hybrid Methods)
由于单一推荐方法各有缺陷,实际系统会把多种方法"混合"使用。
- 把基于内容的方法加入协同过滤(Add content-based methods to collaborative filtering)
用物品内容特征解决"新物品冷启动"。给新物品构建 item profile(内容特征),从而用内容相似性从而解决没人评分的问题,等有了评分再交给协同过滤解决。
也可以使用人口统计信息解决"新用户冷启动"(Demographics to deal with new user problem)。先做一个"粗粒度用户画像"包含年龄、性别、地区等,从而给新用户一个初始推荐。 - 实现多个推荐系统,然后融合它们的预测结果。
这里可能用一个线性模型来融合。
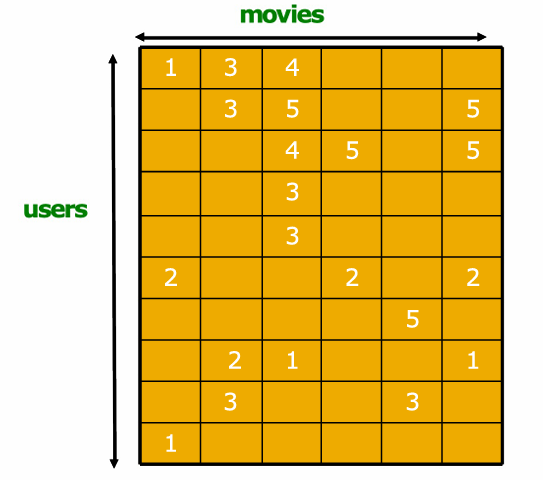
4. 评估推荐系统
这里的方法其实和我们平时的机器学习类似。
我们可以把已有评分藏起来一部分,看系统能不能把它们预测出来。
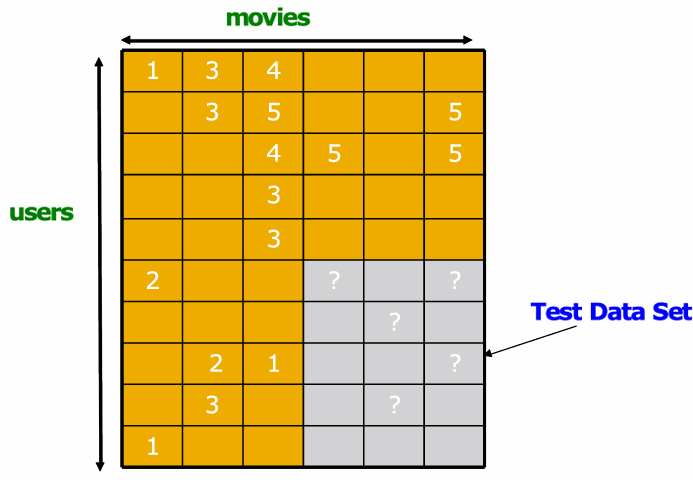
把模型预测的评分,和我们故意藏起来的真实评分作比较,用 RMSE 衡量误差大小。
R M S E = ∑ ( x , i ) ∈ T ( r x i − r x i ∗ ) 2 N \mathrm{RMSE}= \sqrt{ \frac{ \sum_{(x,i)\in T} \left( r_{xi} - r^*_{xi} \right)^2 }{N} } RMSE=N∑(x,i)∈T(rxi−rxi∗)2
其中 N = T N=T N=T, T T T是测试集。
r x i r_{xi} rxi是模型预测的评分。
r x i ∗ r_{xi}^* rxi∗是真实评分(ground truth)。
当然同理,只用 Accuracy(准确率)是不够的,而要看 Precision 和 Recall。
例如网站从最近的评论中,选 10 句话展示给用户,我们需要展示 正面 / 有利于营销的评论,避免展示负面评论。
Precision指的是你预测为正面的内容里,有多少是真的正面。
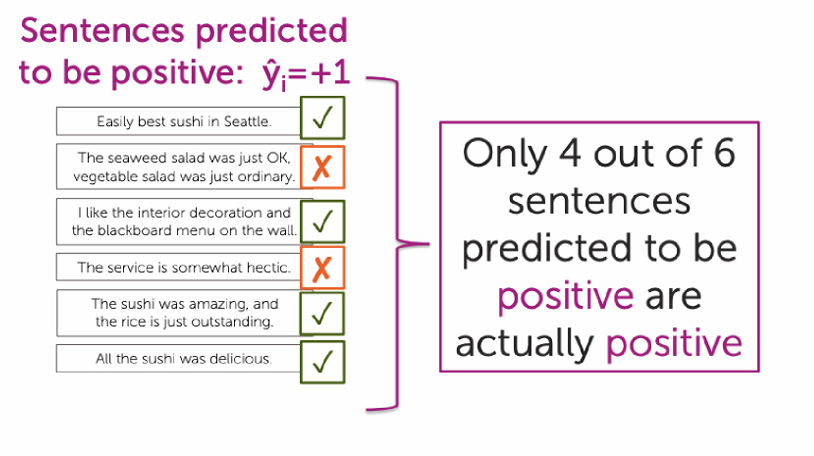
Precision = TP TP + FP \text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}} Precision=TP+FPTP
在这个例子中真正例(TP) = 4
预测为正的总数(TP + FP) = 6
因此代入公式, Precision = 4 6 ≈ 0.67 \text{Precision} = \frac{4}{6} \approx 0.67 Precision=64≈0.67
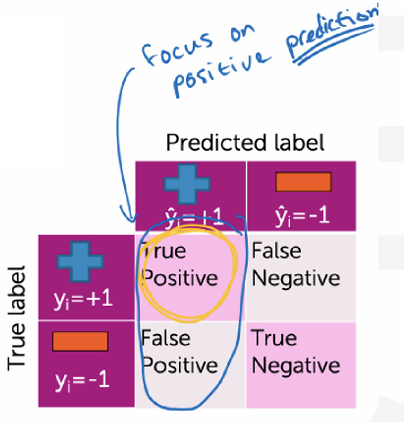
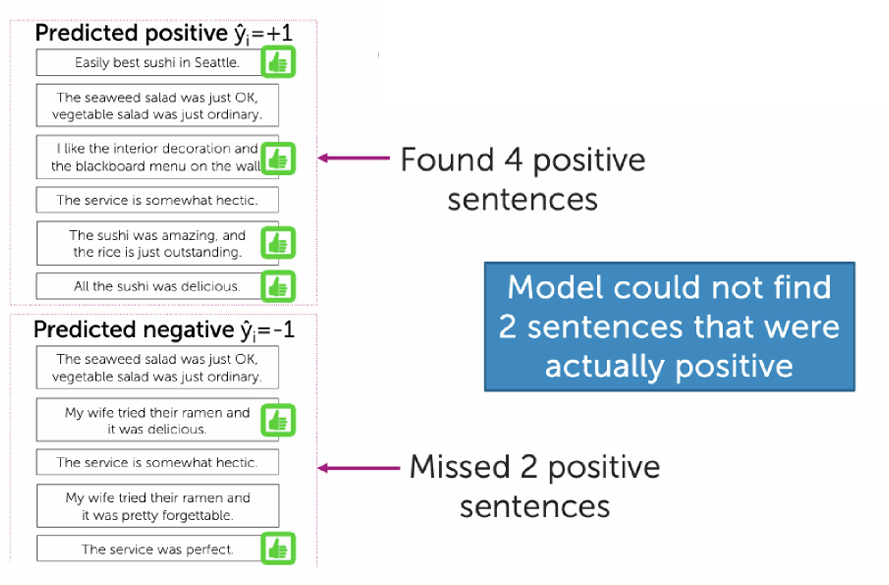
Recall指的是所有"真实为正"的样本里,我找回了多少?换句话说该找的正例中有多少被我找到了?
Recall = TP TP + FN \text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}} Recall=TP+FNTP
在这个例子中真正例(TP) = 4
应该为正的总数是(TP + FN) = 6 ,有2条正例,被我们误判为负例了。
因此代入公式, Recall = 4 6 ≈ 0.67 \text{Recall} = \frac{4}{6} \approx 0.67 Recall=64≈0.67
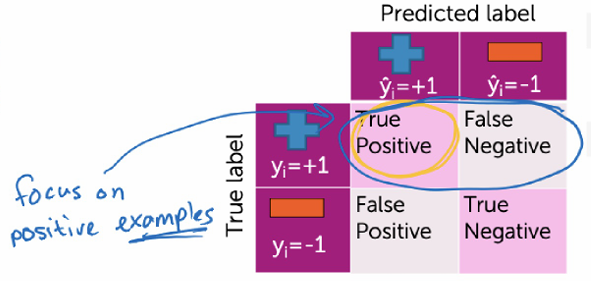
因此我们可以认为Precision表示模型选出来的准不准,而Recall表示该选出来的漏了多少。
放进推荐系统里理解,Accuracy没有什么用,而Precision表示推荐出来的内容,有多少是用户真的喜欢的。而Recall表示用户真正喜欢的内容,有多少被推荐到了。
因此如果我全部放进一样的类,我可能获得极高的正确率,但对应的Precision和Recall会很差。
因此单纯用正确率来评估系统是有问题的。
只盯着 Accuracy / RMSE,容易"跑偏":
- Prediction Diversity(多样性)
一个系统如果总是推荐"大家都爱看的爆款",RMSE 可能很低,但用户体验很差(太无聊)。 - Prediction Context(预测语境)
同样一个推荐,在首页推 vs 在"猜你喜欢"里推包括给新用户 vs 老用户,意义完全不同。但是正确率不会考虑这个场景问题。 - Order of predictions(排序)
推荐系统是 排序问题,用户只看前 5 / 前 10 个,而RMSE 把"排第 1"和"排第 100"看成一样。
现实中,我们只在乎"高分推荐":
- 因此 RMSE 可能会"惩罚好方法",因为可能有一个方法擅长找5分的好物,而对1-3分预测不准。RMSE 会觉得它很差,但是用户觉得其很好。
- 因此我们可以在推荐给用户的前 K 个里使用Precision/Recall。
Top-K Precision:推荐出来的前 K 个中,有多少是用户真实喜欢的?
Top-K Recall:用户真实最喜欢的那些里,有多少被你放进了前 K?