信息学奥赛一本通（部分题解）

1259：【例9.3】求最长不下降序列

C++ 代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 210; // 根据题目 n<=200

int n;
int a[N], f[N], pre[N]; 

// 递归输出路径
void print(int k) {
    if (k == 0) return;
    print(pre[k]);
    cout << a[k] << (f[k] == f[0] ? "" : " "); // f[0] 在这里没用到，只是逻辑占位
}

// 稍微调整一下输出逻辑，用一个临时数组存路径更符合你的习惯
int res[N], cnt;

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];

    int ans = 0, last = 0;
    for (int i = 1; i <= n; i++) {
        f[i] = 1; // 初始化，每个数自成序列长度为1
        for (int j = 1; j < i; j++) {
            if (a[j] <= a[i]) { // 不下降条件
                if (f[j] + 1 > f[i]) {
                    f[i] = f[j] + 1;
                    pre[i] = j; // 记录前驱下标
                }
            }
        }
        if (f[i] > ans) {
            ans = f[i];
            last = i; // 记录最长序列的最后一个位置
        }
    }

    cout << "max=" << ans << endl;

    // 回溯路径
    for (int i = last; i != 0; i = pre[i]) {
        res[++cnt] = a[i];
    }

    // 倒序输出
    for (int i = cnt; i >= 1; i--) {
        cout << res[i] << (i == 1 ? "" : " ");
    }
    cout << endl;

    return 0;
}

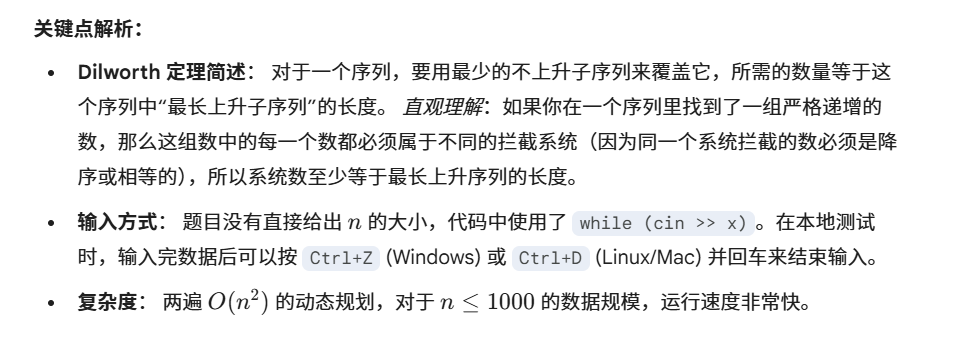
1260：【例9.4】拦截导弹(Noip1999)

C++代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n = 0;
int a[N], f[N];

int main() {
    // 读入数据，题目未给出n，通常使用 while(cin >> x)
    int x;
    while (cin >> x) {
        a[++n] = x;
    }

    // 第一问：最长不上升子序列 (a[j] >= a[i])
    int ans1 = 0;
    for (int i = 1; i <= n; i++) {
        f[i] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j] >= a[i]) {
                f[i] = max(f[i], f[j] + 1);
            }
        }
        ans1 = max(ans1, f[i]);
    }

    // 第二问：最少系统数 = 最长上升子序列 (a[j] < a[i])
    int ans2 = 0;
    // 重置 f 数组用于第二次 DP
    for (int i = 1; i <= n; i++) {
        f[i] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) {
                f[i] = max(f[i], f[j] + 1);
            }
        }
        ans2 = max(ans2, f[i]);
    }

    cout << ans1 << endl;
    cout << ans2 << endl;

    return 0;
}

1261：【例9.5】城市交通路网

C++代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;
const int INF = 1e9; // 定义一个无穷大量

int n;
int a[N][N], f[N], nxt[N];

int main() {
    // 1. 读入城市数量
    if (!(cin >> n)) return 0;

    // 2. 读入费用矩阵
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            cin >> a[i][j];
        }
    }

    // 3. 动态规划：从后往前推
    f[n] = 0; // 终点到终点的距离为0
    for (int i = n - 1; i >= 1; i--) {
        f[i] = INF; // 初始化为无穷大
        for (int j = i + 1; j <= n; j++) {
            // 如果 i 和 j 之间有路，且经过 j 能获得更短路径
            if (a[i][j] > 0 && f[j] != INF) {
                if (a[i][j] + f[j] < f[i]) {
                    f[i] = a[i][j] + f[j];
                    nxt[i] = j; // 记录从 i 往后走的最优决策点
                }
            }
        }
    }

    // 4. 输出结果
    cout << "minlong=" << f[1] << endl;

    // 5. 输出路径
    int curr = 1;
    while (curr != 0) {
        cout << curr << (nxt[curr] == 0 ? "" : " ");
        curr = nxt[curr];
    }
    cout << endl;

    return 0;
}

1262：【例9.6】挖地雷

C++代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 210;

int n;
int w[N];           // 每个地窖的地雷数
int g[N][N];        // 邻接矩阵存储地窖间的连通关系
int f[N];           // DP数组，f[i]表示挖到第i个地窖时的最大地雷数
int pre[N];         // 记录路径前驱
int res[N], cnt;    // 用于最后输出路径

int main() {
    // 1. 输入地窖数量
    cin >> n;

    // 2. 输入每个地窖的地雷数
    for (int i = 1; i <= n; i++) {
        cin >> w[i];
    }

    // 3. 输入连通关系
    int u, v;
    while (cin >> u >> v && (u != 0 || v != 0)) {
        g[u][v] = 1; // 表示从 u 可以到 v
    }

    // 4. 动态规划
    int max_mines = 0;
    int last_node = 0;

    for (int i = 1; i <= n; i++) {
        f[i] = w[i]; // 初始值为该地窖本身的地雷数
        for (int j = 1; j < i; j++) {
            if (g[j][i]) { // 如果从 j 可以到 i
                if (f[j] + w[i] > f[i]) {
                    f[i] = f[j] + w[i];
                    pre[i] = j; // 记录是从哪个地窖挖过来的
                }
            }
        }
        // 更新全局最大值
        if (f[i] > max_mines) {
            max_mines = f[i];
            last_node = i;
        }
    }

    // 5. 回溯路径
    for (int i = last_node; i != 0; i = pre[i]) {
        res[++cnt] = i;
    }

    // 6. 输出结果
    for (int i = cnt; i >= 1; i--) {
        cout << res[i] << (i == 1 ? "" : "-");
    }
    cout << endl;
    cout << max_mines << endl;

    return 0;
}

1263：【例9.7】友好城市

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 5010;

// 定义城市对结构体
struct City {
    int s, n; // s: 南岸坐标, n: 北岸坐标
} a[N];

// 排序规则：按南岸坐标从小到大排
bool cmp(City x, City y) {
    return x.s < y.s;
}

int n;
int f[N]; // DP数组，f[i] 表示以第 i 个城市结尾的最长上升子序列长度

int main() {
    // 1. 输入数据
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i].s >> a[i].n;
    }

    // 2. 预处理：按南岸坐标排序
    sort(a + 1, a + n + 1, cmp);

    // 3. 动态规划求解北岸坐标的最长上升子序列
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        f[i] = 1; // 初始长度为1
        for (int j = 1; j < i; j++) {
            // 如果北岸坐标也是上升的，则可以构成不相交航道
            if (a[j].n < a[i].n) {
                f[i] = max(f[i], f[j] + 1);
            }
        }
        // 更新全局最大值
        ans = max(ans, f[i]);
    }

    // 4. 输出结果
    cout << ans << endl;

    return 0;
}

1264：【例9.8】合唱队形

C++代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n;
int a[N], f[N], g[N];

int main() {
    // 1. 输入学生总数和身高
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    // 2. 从左向右计算最长上升子序列 (LIS)
    for (int i = 1; i <= n; i++) {
        f[i] = 1; // 初始长度为1
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) {
                f[i] = max(f[i], f[j] + 1);
            }
        }
    }

    // 3. 从右向左计算最长上升子序列 (相当于从左往右的最长下降子序列)
    for (int i = n; i >= 1; i--) {
        g[i] = 1; // 初始长度为1
        for (int j = n; j > i; j--) {
            if (a[j] < a[i]) {
                g[i] = max(g[i], g[j] + 1);
            }
        }
    }

    // 4. 计算最大合唱队人数
    int max_k = 0;
    for (int i = 1; i <= n; i++) {
        if (f[i] + g[i] - 1 > max_k) {
            max_k = f[i] + g[i] - 1;
        }
    }

    // 5. 输出最少出列人数 = 总人数 - 最大合唱队人数
    cout << n - max_k << endl;

    return 0;
}

1265：【例9.9】最长公共子序列

C++代码实现

cpp 复制代码

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

const int N = 1010;

string s1, s2;
int f[N][N];

int main() {
    // 1. 读入两个字符串
    // 由于字符串可能包含空格，但在本题描述中是大写字母，直接用cin即可
    if (!(cin >> s1 >> s2)) return 0;

    int n = s1.length();
    int m = s2.length();

    // 2. 动态规划过程
    // 为了方便对应 f[i][j] 的逻辑，下标从 1 开始
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            // 注意字符串下标从 0 开始，所以比较时用 i-1 和 j-1
            if (s1[i - 1] == s2[j - 1]) {
                f[i][j] = f[i - 1][j - 1] + 1;
            } else {
                f[i][j] = max(f[i - 1][j], f[i][j - 1]);
            }
        }
    }

    // 3. 输出最长公共子序列的长度
    cout << f[n][m] << endl;

    return 0;
}

1266：【例9.10】机器分配

C++代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int MAXN = 15;
const int MAXM = 20;

int n, m;
int w[MAXN][MAXM];    // w[i][j] 表示第 i 个公司分 j 台机器的盈利
int f[MAXN][MAXM];    // f[i][j] 状态数组
int way[MAXN][MAXM];  // way[i][j] 记录第 i 个公司在当前最优决策下分得的机器数
int res[MAXN];        // 存储最终每个公司的分配方案

int main() {
    // 1. 输入数据
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            cin >> w[i][j];
        }
    }

    // 2. 动态规划过程
    for (int i = 1; i <= n; i++) {           // 枚举分公司
        for (int j = 0; j <= m; j++) {       // 枚举总机器数
            for (int k = 0; k <= j; k++) {   // 枚举给当前第 i 个公司分 k 台
                if (f[i - 1][j - k] + w[i][k] >= f[i][j]) {
                    f[i][j] = f[i - 1][j - k] + w[i][k];
                    way[i][j] = k;           // 记录第 i 个公司分了 k 台
                }
            }
        }
    }

    // 3. 输出最大盈利
    cout << f[n][m] << endl;

    // 4. 回溯分配方案
    int curr_m = m;
    for (int i = n; i >= 1; i--) {
        res[i] = way[i][curr_m];
        curr_m -= res[i]; // 剩余机器数减去已分配的
    }

    // 5. 输出每家公司的分配情况
    for (int i = 1; i <= n; i++) {
        cout << i << " " << res[i] << endl;
    }

    return 0;
}

1281：最长上升子序列

C++代码实现

cpp 复制代码

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010; // 假设 N 最大为 1000

int n;
int a[N], f[N];

int main() {
    // 1. 输入数据
    if (!(cin >> n)) return 0;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }

    // 2. 动态规划过程
    int ans = 0;
    for (int i = 1; i <= n; i++) {
        f[i] = 1; // 每一个数初始化长度为 1
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) { // 严格上升条件
                f[i] = max(f[i], f[j] + 1);
            }
        }
        // 在计算过程中顺便记录全局最大值
        ans = max(ans, f[i]);
    }

    // 3. 输出最长长度
    cout << ans << endl;

    return 0;
}