LeetCode 3453.分割正方形 I：二分查找

【LetMeFly】3453.分割正方形 I：二分查找

力扣题目链接：https://leetcode.cn/problems/separate-squares-i/

给你一个二维整数数组 squares ，其中 squares[i] = [x_i, y_i, l_i] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。

找到一个最小的 y 坐标，它对应一条水平线，该线需要满足它以上正方形的总面积等于该线以下正方形的总面积。

答案如果与实际答案的误差在 10^-5 以内，将视为正确答案。

注意：正方形 可能会 重叠。重叠区域应该被 多次计数。

示例 1：
输入： squares = [[0,0,1],[2,2,1]]

输出： 1.00000

解释：

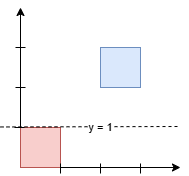
任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方，1 平方单位的面积在其下方。最小的 y 坐标是 1。

示例 2：
输入： squares = [[0,0,2],[1,1,1]]

输出： 1.16667

解释：

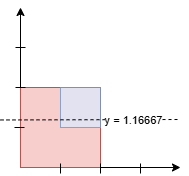
面积如下：

线下的面积：7/6 * 2 (红色) + 1/6 (蓝色) = 15/6 = 2.5。
线上的面积：5/6 * 2 (红色) + 5/6 (蓝色) = 15/6 = 2.5。

由于线以上和线以下的面积相等，输出为 7/6 = 1.16667。

提示：

1 <= squares.length <= 5 * 10⁴
squares[i] = [x_i, y_i, l_i]
squares[i].length == 3
0 <= x_i, y_i <= 10⁹
1 <= l_i <= 10⁹
所有正方形的总面积不超过 10¹²。

解题方法：二分查找

先算下所有正方形的总面积，然后二分分割线高度，太低就高点太高就低点。

终止条件：两次计算结果分割线移动返回不超过 10 − 5 10^{-5} 10−5或直接进行 50 50 50次求值。

python 复制代码

>>> 10**9 / 2**46
1.4210854715202004e-05
>>> 10**9 / 2**47
7.105427357601002e-06

时间复杂度 O ( C × l e n ( s q u a r e s ) ) O(C\times len(squares)) O(C×len(squares))，其中 C = 50 C=50 C=50或 C = log ⁡ 2 m a x ( s q u i r e s [ i ] [ 1 ] ) − m i n ( s q u i r e s [ i ] [ 1 ] ) C=\log_2{max(squires[i][1])-min(squires[i][1])} C=log2max(squires[i][1])−min(squires[i][1])
空间复杂度 O ( 1 ) O(1) O(1)

AC代码

C++

cpp 复制代码

/*
 * @LastEditTime: 2026-01-13 22:21:20
 */
class Solution {
private:
    double half = 0;
    vector<vector<int>> squares;

    bool check(double h) {
        double total = 0;
        for (vector<int>& s : squares) {
            double from = max(double(s[1]), h);
            double to = s[1] + s[2];
            total += max(0., (to - from) * s[2]);
        }

        return total > half;
    }
public:
    double separateSquares(vector<vector<int>>& squares) {
        long long total = 0;  // !!!!!记得初始化
        for (vector<int>& s : squares) {
            total += ((long long) s[2]) * s[2];
        }
        this->squares = move(squares);
        half = 1. * total / 2;

        double l = 0, r = 1000000000;
        for (int _ = 0; _ < 50; _++) {
            double mid = (l + r) / 2;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid;
            }
        }
        return l;
    }
};

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源