leetcode 3453. 分割正方形 I 中等

给你一个二维整数数组 squares ，其中 squares[i] = [xi, yi, li] 表示一个与 x 轴平行的正方形的左下角坐标和正方形的边长。

找到一个最小的 y 坐标，它对应一条水平线，该线需要满足它以上正方形的总面积等于该线以下正方形的总面积。

答案如果与实际答案的误差在 10^-5 以内，将视为正确答案。

注意：正方形 可能会 重叠。重叠区域应该被 多次计数。

示例 1：

输入： squares = $\[0,0,1$ , $2,2,1$ ]

输出： 1.00000

解释：

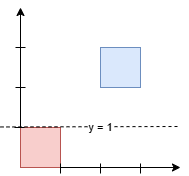
任何在 y = 1 和 y = 2 之间的水平线都会有 1 平方单位的面积在其上方，1 平方单位的面积在其下方。最小的 y 坐标是 1。

示例 2：

输入： squares = $\[0,0,2$ , $1,1,1$ ]

输出： 1.16667

解释：

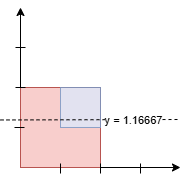
面积如下：

线下的面积：7/6 * 2 (红色) + 1/6 (蓝色) = 15/6 = 2.5。
线上的面积：5/6 * 2 (红色) + 5/6 (蓝色) = 15/6 = 2.5。

由于线以上和线以下的面积相等，输出为 7/6 = 1.16667。

提示：

1 <= squares.length <= 5 * 10^4
squares[i] = [xi, yi, li]
squares[i].length == 3
0 <= xi, yi <= 10^9
1 <= li <= 10^9
所有正方形的总面积不超过 10^12。

分析：浮点二分答案，设当前的上界为 r，下界为 l，中线为 mid。分别计算当前答案的上方和下方面积和，如果面积差小于 10 的 -5 次方，则可将 r=mid；否则 l=mid。因为题目要求答案误差范围在 10 的 -5 次方内，所以结束条件为 r-l<0.00001。

cpp 复制代码

double separateSquares(int** squares, int squaresSize, int* squaresColSize) {
    double ans=0;
    int low=squares[0][1],high=squares[0][1]+squares[0][2];
    for(int i=1;i<squaresSize;++i)
        low=fmin(low,squares[i][1]),high=fmax(high,squares[i][1]+squares[i][2]);
    double l=low,r=high;
    while(l<r)
    {
        double mid=(l+r)/2.0,area_l=0.0,area_h=0.0;
        for(int i=0;i<squaresSize;++i)
        {
            if(mid<=squares[i][1])area_h+=1.0*squares[i][2]*squares[i][2];
            else if(mid>=squares[i][1]+squares[i][2])area_l+=1.0*squares[i][2]*squares[i][2];
            else
            {
                double temp=squares[i][2]*1.0*(squares[i][1]+squares[i][2]-mid);
                area_h+=temp,area_l+=1.0*squares[i][2]*squares[i][2]-temp;
            }
        }
        if(area_h<=area_l)r=mid;
        else if(area_h>area_l)l=mid;

        // printf("l=%f r=%f mid=%f\n",l,r,mid);
        if(r-l<=0.00001)
        {
            ans=l;break;
        }
    }
    return ans;
}