信奥赛C++提高组csp-s之KMP算法详解

一、KMP算法概述
KMP算法(Knuth-Morris-Pratt算法)是一种高效的字符串匹配算法,用于在文本串中查找模式串的出现位置。与朴素的暴力匹配相比,KMP算法的时间复杂度为O(n+m),其中n是文本串长度,m是模式串长度。
二、核心思想:利用已匹配信息避免重复比较
朴素算法的缺点
cpp
// 暴力匹配示例
for (int i = 0; i <= n - m; i++) {
bool found = true;
for (int j = 0; j < m; j++) {
if (text[i + j] != pattern[j]) {
found = false;
break;
}
}
if (found) {
// 找到匹配
}
}
// 时间复杂度:O(n*m)KMP算法的核心是:当出现不匹配时,利用已知信息,将模式串向右滑动尽可能远的距离,而不是每次只移动一位。
三、关键概念:前缀函数(next数组)
1. 什么是前缀函数?
- 对于模式串P的每个位置i(1≤ i ≤ m),定义前缀函数nxt[i]表示:
- 子串P[1:i]的最长相同真前缀和真后缀的长度
- 真前缀:不包括字符串本身的前缀
- 真后缀:不包括字符串本身的后缀
2. next数组的作用
- 记录匹配失败时,模式串应该回退到哪个位置继续匹配
- 避免主串指针回退,保持O(n)的时间复杂度
四、next数组的构造(重点!)
1. 理解前缀和后缀
对于字符串"ababa":
- 真前缀有:"a", "ab", "aba", "abab"
- 真后缀有:"a", "ba", "aba", "baba"
最长公共前后缀:"aba",长度为3
2. next数组的手动计算过程
以模式串"ABABCABAA"为例(备注:举例中的字符串下标从1开始):
步骤分解:
模式串:A B A B C A B A A
索引: 1 2 3 4 5 6 7 8 9
next: 0 0 1 2 0 1 2 3 1计算过程详解:
- i=1: 子串"A" → 没有真前缀和真后缀 → next[1]=0
- i=2: 子串"AB" → 前缀{"A"},后缀{"B"} → 无公共 → next[2]=0
- i=3: 子串"ABA" → 前缀{"A","AB"},后缀{"A","BA"} → 最长公共"A" → next[3]=1
- i=4: 子串"ABAB" → 前缀{"A","AB","ABA"},后缀{"B","AB","BAB"} → 最长公共"AB" → next[4]=2
- i=5: 子串"ABABC" → 无公共前后缀 → next[5]=0
- i=6: 子串"ABABCA" → 最长公共"A" → next[6]=1
- i=7: 子串"ABABCAB" → 最长公共"AB" → next[7]=2
- i=8: 子串"ABABCABA" → 最长公共"ABA" → next[8]=3
- i=9: 子串"ABABCABAA" → 最长公共"A" → next[9]=1
3.next数组的构造算法思想
构造next数组的过程本质上是模式串的自我匹配:
- 初始化:next[1] = 0,设j = 0(j表示当前已匹配的前缀长度)
- 递推计算 :对于i从1到m-1(m为模式串长度)
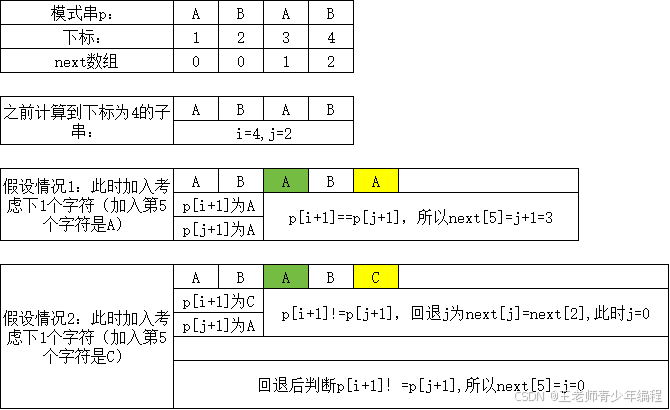
- 如果p[i+1] == p[j+1],则j++,next[i+1] = j
- 否则,将j回退到next[j],继续比较
- 如果j回退到0仍不匹配,则next[i] = 0
关键理解:
-
j实际上表示当前位置之前的最长匹配前缀的长度
-
当p[i+1] != p[j+1]时,我们不是从头开始,而是利用已经计算好的next[j]来回退
-
我们可以把next数组看作一个状态转移函数:
- 当前状态为j(已匹配的长度)
- 如果下一个字符匹配成功,转移到状态j+1
- 如果下一个字符匹配失败,转移到状态next[j]
4. next数组的代码实现
cpp
nxt[0] = 0; // 边界条件,空字符串的border长度为0
nxt[1] = 0; // 单个字符没有非自身的border,长度为0
// 计算nxt[2]到nxt[len_p]
for (int i = 1, j = 0; i < len_p; i++) {// i从1开始,实际计算的是nxt[i+1],j表示当前已匹配的前缀长度
// 当j>0且下一个字符不匹配时,利用已知的next信息回溯j
while (j > 0 && p[i + 1] != p[j + 1]) {
j = nxt[j]; // 回溯到前一个可能匹配的位置
}
// 如果下一个字符匹配,则增加匹配长度
if (p[i + 1] == p[j + 1]) {
j++;
}
// 记录当前前缀的最长border长度
nxt[i + 1] = j; // nxt[i+1] = 前缀p[1...i+1]的最长border长度
}五、KMP匹配过程详解
示例:在文本串中查找模式串(备注:举例中的字符串S和P的下标从1开始)
文本串s: "ABABDABACDABABCABAB"
模式串p: "ABABCABAB"
next数组: [0, 0, 1, 2, 0, 1, 2, 3, 4]
1 2 3 4 5 6 7 8 9 (模式串索引)匹配过程:
-
首次失配(位置5):
文本串:ABAB D ... 模式串:ABAB C ... 已匹配:ABAB (j=4) 失配字符:D vs C- 执行
j = next[4] = 2 - 模式串滑动:比较文本串的D与模式串的
p[3]=A - 继续失配,
j = next[2] = 0 - 最终从模式串开头重新比较
- 执行
-
完全匹配(位置11-19):
文本串位置:11 12 13 14 15 16 17 18 19 文本串字符:A B A B C A B A B 模式串字符:A B A B C A B A B 匹配过程:逐步匹配,j从0增加到9- 匹配成功后输出位置:
i - len(p) + 2 = 18 - 9 + 2 = 11 - 继续:
j = next[9] = 4,准备可能的重叠匹
- 匹配成功后输出位置:
KMP匹配的代码实现:
cpp
for (int i = 0, j = 0; i < len_s; i++) { // i遍历文本串,j表示当前匹配的模式串长度
// 当字符不匹配且j>0时,利用next数组回溯j,避免文本串指针i回退
while (j > 0 && s[i + 1] != p[j + 1]) {
j = nxt[j]; // 模式串向右滑动
}
// 当前字符匹配,模式串匹配长度加1
if (s[i + 1] == p[j + 1]) {
j++;
}
// 如果完全匹配模式串
if (j == len_p) {
// 输出匹配位置:当前文本串位置i+1减去模式串长度再加1
// 因为字符串从1开始索引,所以起始位置为 i - len_p + 2
printf("%d\n", i - len_p + 2);
// 继续寻找下一个匹配:将j设为当前匹配串的最长border长度
j = nxt[j];
}
}研究案例
题目描述
给出两个字符串 s 1 s_1 s1 和 s 2 s_2 s2,若 s 1 s_1 s1 的区间 [ l , r ] [l, r] [l,r] 子串与 s 2 s_2 s2 完全相同,则称 s 2 s_2 s2 在 s 1 s_1 s1 中出现了,其出现位置为 l l l。
现在请你求出 s 2 s_2 s2 在 s 1 s_1 s1 中所有出现的位置。
定义一个字符串 s s s 的 border 为 s s s 的一个非 s s s 本身 的子串 t t t,满足 t t t 既是 s s s 的前缀,又是 s s s 的后缀。
对于 s 2 s_2 s2,你还需要求出对于其每个前缀 s ′ s' s′ 的最长 border t ′ t' t′ 的长度。
输入格式
第一行为一个字符串,即为 s 1 s_1 s1。
第二行为一个字符串,即为 s 2 s_2 s2。
输出格式
首先输出若干行,每行一个整数,按从小到大的顺序 输出 s 2 s_2 s2 在 s 1 s_1 s1 中出现的位置。
最后一行输出 ∣ s 2 ∣ |s_2| ∣s2∣ 个整数,第 i i i 个整数表示 s 2 s_2 s2 的长度为 i i i 的前缀的最长 border 长度。
输入 #1
ABABABC
ABA输出 #1
1
3
0 0 1说明/提示
样例 1 解释
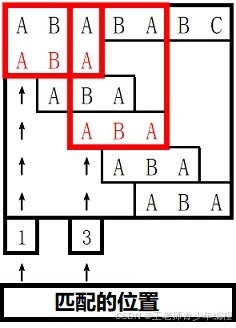
对于 s 2 s_2 s2 长度为 3 3 3 的前缀 ABA,字符串 A 既是其后缀也是其前缀,且是最长的,因此最长 border 长度为 1 1 1。
数据规模与约定
本题采用多测试点捆绑测试,共有 4 个子任务。
- Subtask 0(30 points): ∣ s 1 ∣ ≤ 15 |s_1| \leq 15 ∣s1∣≤15, ∣ s 2 ∣ ≤ 5 |s_2| \leq 5 ∣s2∣≤5。
- Subtask 1(40 points): ∣ s 1 ∣ ≤ 10 4 |s_1| \leq 10^4 ∣s1∣≤104, ∣ s 2 ∣ ≤ 10 2 |s_2| \leq 10^2 ∣s2∣≤102。
- Subtask 2(30 points):无特殊约定。
- Subtask 3(0 points):Hack。
对于全部的测试点,保证 1 ≤ ∣ s 1 ∣ , ∣ s 2 ∣ ≤ 10 6 1 \leq |s_1|,|s_2| \leq 10^6 1≤∣s1∣,∣s2∣≤106, s 1 , s 2 s_1, s_2 s1,s2 中均只含大写英文字母。
代码实现
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10; // 定义足够大的数组大小,满足题目数据范围
char s[N], p[N]; // s为文本串,p为模式串,下标从1开始
int nxt[N]; // next数组,nxt[i]表示模式串前i个字符组成的前缀的最长border长度
int main() {
// 输入字符串,从下标1开始存储
scanf("%s%s", s + 1, p + 1);
int len_s = strlen(s + 1); // 文本串长度
int len_p = strlen(p + 1); // 模式串长度
// ---------- 第一部分:计算模式串的next数组(前缀函数) ----------
nxt[0] = 0; // 边界条件,空字符串的border长度为0
nxt[1] = 0; // 单个字符没有非自身的border,长度为0
// 计算nxt[2]到nxt[len_p]
for (int i = 1, j = 0; i < len_p; i++) { // i从1到len_p-1,实际计算的是nxt[i+1]
// 当j>0且下一个字符不匹配时,利用已知的next信息回溯j
while (j > 0 && p[i + 1] != p[j + 1]) {
j = nxt[j]; // 回溯到前一个可能匹配的位置
}
// 如果下一个字符匹配,则增加匹配长度
if (p[i + 1] == p[j + 1]) {
j++;
}
// 记录当前前缀的最长border长度
nxt[i + 1] = j; // nxt[i+1] = 前缀p[1...i+1]的最长border长度
}
// ---------- 第二部分:KMP匹配过程 ----------
for (int i = 0, j = 0; i < len_s; i++) { // i遍历文本串,j表示当前匹配的模式串长度
// 当字符不匹配且j>0时,利用next数组回溯j,避免文本串指针i回退
while (j > 0 && s[i + 1] != p[j + 1]) {
j = nxt[j]; // 模式串向右滑动
}
// 当前字符匹配,模式串匹配长度加1
if (s[i + 1] == p[j + 1]) {
j++;
}
// 如果完全匹配模式串
if (j == len_p) {
// 输出匹配位置:当前文本串位置i+1减去模式串长度再加1
// 因为字符串从1开始索引,所以起始位置为 i - len_p + 2
printf("%d\n", i - len_p + 2);
// 继续寻找下一个匹配:将j设为当前匹配串的最长border长度
j = nxt[j];
}
}
// ---------- 第三部分:输出模式串每个前缀的最长border长度 ----------
for (int i = 1; i <= len_p; i++) {
printf("%d ", nxt[i]);
}
return 0;
}功能分析
1. 算法目标
- 实现KMP字符串匹配算法,解决两个问题:
a) 找出模式串在文本串中所有出现的位置
b) 计算模式串每个前缀的最长border长度
2. 核心数据结构
nxt[]数组:存储模式串的"前缀函数"值,nxt[i]表示子串p[1...i]的最长border长度- 定义:border是字符串的非本身的前缀,且同时是该字符串的后缀
- 例如:
"ABA"的最长border是"A",长度为1
3. 算法流程
第一步:预处理模式串(计算next数组)
- 目的:得到模式串的"自匹配"信息,用于匹配失败时快速跳过不必要的比较
- 关键操作 :
- 初始化
nxt[0]=0, nxt[1]=0 - 使用双指针
i和j:i:当前正在计算的前缀的结束位置(实际代码中i从1开始,计算nxt[i+1])j:当前已匹配的前缀长度,也指向下一个待比较字符
- 循环中不断尝试扩展匹配长度,失败时通过
j = nxt[j]回溯到更短的匹配前缀
- 初始化
- 时间复杂度:O(len_p)
第二步:文本串匹配
- 目的:在文本串中找到所有模式串出现的位置
- 关键操作 :
- 双指针
i(文本串指针)和j(模式串匹配长度) - 不匹配时,
j通过nxt数组回溯,i永不回退 - 匹配成功时输出位置,并继续通过
nxt[j]寻找下一个可能的匹配
- 双指针
- 时间复杂度:O(len_s)
4. 算法特点
- 时间复杂度:O(len_s + len_p),线性复杂度
- 空间复杂度:O(len_p),用于存储next数组
- 核心优势:通过next数组避免文本串指针回退,显著提高效率
5. 代码细节说明
- 字符串存储:从下标1开始存储,方便与next数组下标对齐
- 边界处理 :
- 模式串长度为1时,next数组计算循环不执行,直接使用初始值
- 匹配成功后执行
j = nxt[j],确保不遗漏重叠匹配(如文本串"AAAA"中找模式串"AA")
- 位置计算 :匹配位置计算公式为
i - len_p + 2i:当前循环变量(从0开始)len_p:模式串长度+2:补偿下标从1开始和匹配结束位置到起始位置的转换
6. 示例验证
对于输入:
ABABABC
ABA程序执行:
-
计算next数组:
nxt[1]=0, nxt[2]=0, nxt[3]=1 -
匹配过程:
- 位置1匹配成功(
ABA) - 位置3匹配成功(
ABA)
- 位置1匹配成功(
-
输出:
1 3 0 0 1
更多系列知识,请查看专栏:《信奥赛C++提高组csp-s知识详解及案例实践》:
https://blog.csdn.net/weixin_66461496/category_13113932.html
各种学习资料,助力大家一站式学习和提升!!!
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<"########## 一站式掌握信奥赛知识! ##########";
cout<<"############# 冲刺信奥赛拿奖! #############";
cout<<"###### 课程购买后永久学习,不受限制! ######";
return 0;
}1、csp信奥赛高频考点知识详解及案例实践:
CSP信奥赛C++动态规划:
https://blog.csdn.net/weixin_66461496/category_13096895.html点击跳转
CSP信奥赛C++标准模板库STL:
https://blog.csdn.net/weixin_66461496/category_13108077.html 点击跳转
信奥赛C++提高组csp-s知识详解及案例实践:
https://blog.csdn.net/weixin_66461496/category_13113932.html
2、csp信奥赛冲刺一等奖有效刷题题解:
CSP信奥赛C++初赛及复赛高频考点真题解析(持续更新):https://blog.csdn.net/weixin_66461496/category_12808781.html 点击跳转
CSP信奥赛C++一等奖通关刷题题单及题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12673810.html 点击跳转
3、GESP C++考级真题题解:

GESP(C++ 一级+二级+三级)真题题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12858102.html 点击跳转

GESP(C++ 四级+五级+六级)真题题解(持续更新):https://blog.csdn.net/weixin_66461496/category_12869848.html 点击跳转
GESP(C++ 七级+八级)真题题解(持续更新):
https://blog.csdn.net/weixin_66461496/category_13117178.html
4、CSP信奥赛C++竞赛拿奖视频课:
https://edu.csdn.net/course/detail/40437 点击跳转

· 文末祝福 ·
cpp
#include<bits/stdc++.h>
using namespace std;
int main(){
cout<<"跟着王老师一起学习信奥赛C++";
cout<<" 成就更好的自己! ";
cout<<" csp信奥赛一等奖属于你! ";
return 0;
}