3454: 分割正方形Ⅱ
扫描线模板题:矩形面积并
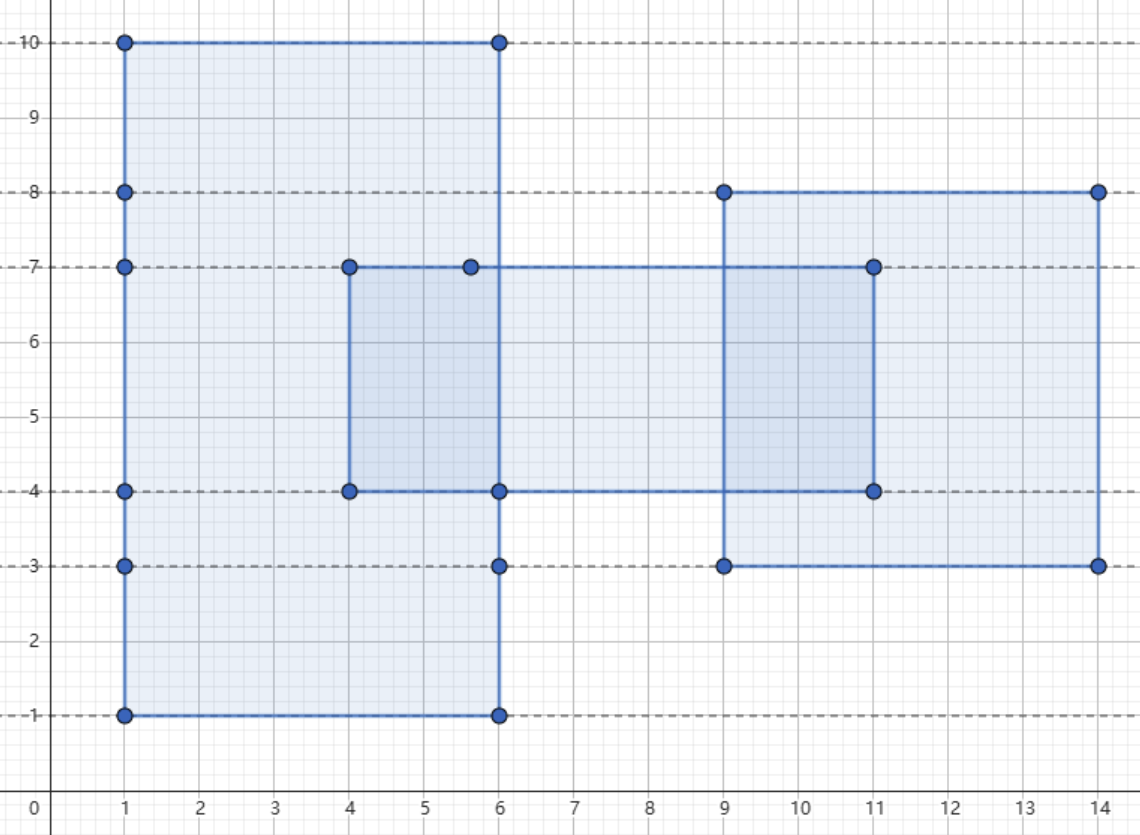
我们以上图的三个矩形为例,讲述如何求它们面积的并。我们对每个矩形的上边界和下边界都画一条水平线,可以看出,相邻水平线之间,矩形的横截长度都是一样的。因此,相邻水平线之间矩形面积的并,就等于横截长度乘以水平线的高度差。问题转为如何求矩形的横截长度。
我们来看相邻的水平线之间,矩形的横截长度发生了什么变化。
- 在 y=1 时,横截长度只是区间 [1,6] 的长度,即 5。所以 y=1 到 y=3 之间的面积是 (3−1)×5=10。
- 到了 y=3 时,由于新矩形的加入,区间数量增加了一个,变成 [1,6]∪[9,14] 的长度,即 10。所以 y=3 到 y=4 之间的面积是 (4−3)×10=10。
- 到了 y=4 时,由于新矩形的加入,区间数量又增加了一个,变成 [1,6]∪[4,11]∪[9,14]=[1,14] 的长度,即 13。所以 y=4 到 y=7 之间的面积是 (7−4)×13=39。
- 到了 y=7 时,由于一个矩形的退出,区间的数量减少了一个,变成 [1,6]∪[9,14] 的长度,即 10。所以 y=7 到 y=8 之间的面积是 (8−7)×10=10。
- 到了 y=8 时,由于一个矩形的退出,区间的数量又减少了一个,变成 [1,6] 的长度,即 5。所以 y=8 到 y=10 之间的面积是 (10−8)×5=10。
所以矩形面积并为 10+10+39+10+10=79。
从上面的例子可以看出,横截长度的变化,其实就是维护一个区间的集合。每次我要加入或删除一个区间,然后求区间并集的长度。

因为操作涉及到了区间修改 + 区间查询,我们可以用懒标记下推线段树完成操作的维护。这样我们就成功维护了横截长度。最后的问题是找到最下面的水平线,使得水平线下方的面积并减去水平线上方的面积并大等于 0。

class Solution {
public:
double separateSquares(vector<vector<int>>& squares) {
int n = squares.size(), m = 0;
map<int, int> mp; // 默认升序
for (auto &sq : squares) { // 标记正方形的左右 x 端点
mp[sq[0]] = 1;
mp[sq[0] + sq[2]] = 1;
}
for (auto &p : mp) p.second = m++; // 离散化:x 坐标 -> 0,1,2...
vector<int> A(m); // 反查表 A[i] = 第 i 个端点坐标
for (auto &p : mp) A[p.second] = p.first;
/* -------- 线段树部分 -------- */
struct Node {
int mn, len, lazy;
void add(int v) { mn += v; lazy += v; }
};
vector<Node> tree(m * 4); // 足够大的线段树
// 合并左右子节点
auto merge = [&](const Node& L, const Node& R) {
int mn = min(L.mn, R.mn);
int lsum = (L.mn == mn ? L.len : 0) + (R.mn == mn ? R.len : 0);
return Node{mn, lsum, 0};
};
// 下推懒标记
auto down = [&](int id) {
if (!tree[id].lazy) return;
int lc = id << 1, rc = lc | 1;
tree[lc].add(tree[id].lazy);
tree[rc].add(tree[id].lazy);
tree[id].lazy = 0;
};
// 建树
function<void(int,int,int)> build = [&](int id,int l,int r) {
if (l == r) tree[id] = {0, A[r] - A[r-1], 0};
else {
int mid = (l + r) >> 1;
build(id<<1, l, mid);
build(id<<1|1, mid+1, r);
tree[id] = merge(tree[id<<1], tree[id<<1|1]);
}
};
// 区间 [ql,qr] 加减 qv
function<void(int,int,int,int,int,int)> modify = [&](int id,int l,int r,int ql,int qr,int qv) {
if (ql <= l && r <= qr) { tree[id].add(qv); return; }
down(id);
int mid = (l + r) >> 1;
if (ql <= mid) modify(id<<1, l, mid, ql, qr, qv);
if (qr > mid) modify(id<<1|1, mid+1, r, ql, qr, qv);
tree[id] = merge(tree[id<<1], tree[id<<1|1]);
};
/* -------- 线段树部分结束 -------- */
// 扫描线事件:y, x1_idx, x2_idx, ±1
vector<array<int,4>> vec;
for (auto &sq : squares) {
int x1 = mp[sq[0]], x2 = mp[sq[0] + sq[2]];
vec.push_back({sq[1], x1+1, x2, 1});
vec.push_back({sq[1]+sq[2], x1+1, x2, -1});
}
sort(vec.begin(), vec.end());
// 第一遍:求总并面积 tot
build(1, 1, m-1);
long long tot = 0;
for (int i = 0; i + 1 < (int)vec.size(); ++i) {
modify(1, 1, m-1, vec[i][1], vec[i][2], vec[i][3]);
int len = A[m-1] - A[0];
if (tree[1].mn == 0) len -= tree[1].len;
tot += (long long)len * (vec[i+1][0] - vec[i][0]);
}
// 第二遍:边扫边算 delta
build(1, 1, m-1);
long long now = 0;
for (int i = 0; i + 1 < (int)vec.size(); ++i) {
modify(1, 1, m-1, vec[i][1], vec[i][2], vec[i][3]);
int len = A[m-1] - A[0];
if (tree[1].mn == 0) len -= tree[1].len;
now += (long long)len * (vec[i+1][0] - vec[i][0]);
long long det = now - (tot - now);
if (det >= 0) // 找到分割线
return vec[i+1][0] - 0.5 * det / len;
}
return -1;
}
};