一、能控性与能观性的定义
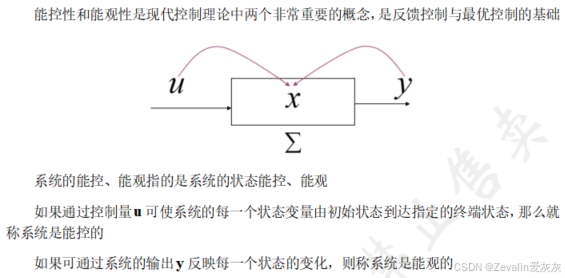
二、线性定常系统的能控性
1、线性定常系统能控性的定义
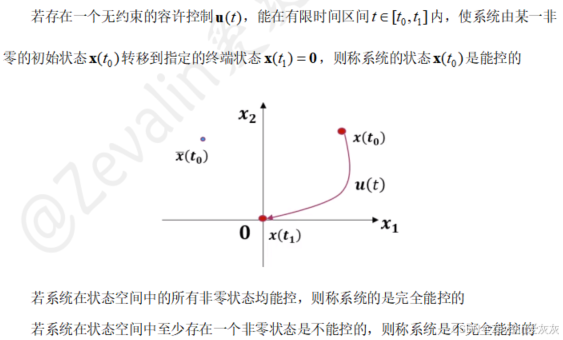
2、线性定常系统的能控性的描述
(1)由系统完全能控的定义,若系统在状态空间中任一非零的初始状态,均能找到一个容许控制,使系统在有限的时间内转移到平衡状态,则称系统是完全能控的。
(2)完全能控的数学描述:

3、Gram(格拉姆)矩阵判据
(1)Gram(格拉姆)矩阵判据内容:

(2)Gram(格拉姆)矩阵判据充分性证明:

(3)Gram(格拉姆)矩阵判据必要性证明:


4、秩判据
(1)秩判据内容:

(2)秩判据充分性证明:

(3)秩判据必要性证明:

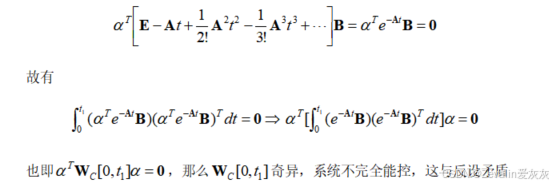
(4)秩判据的应用举例:

5、PBH秩判据
(1)PBH秩判据内容:

(2)PBH秩判据必要性证明:

(3)PBH秩判据充分性证明:
充分性需应用能控性分解进行证明,此处就不详细展开了
(4)PBH秩判据的应用举例:

6、规范型判据
(1)规范型判据内容:
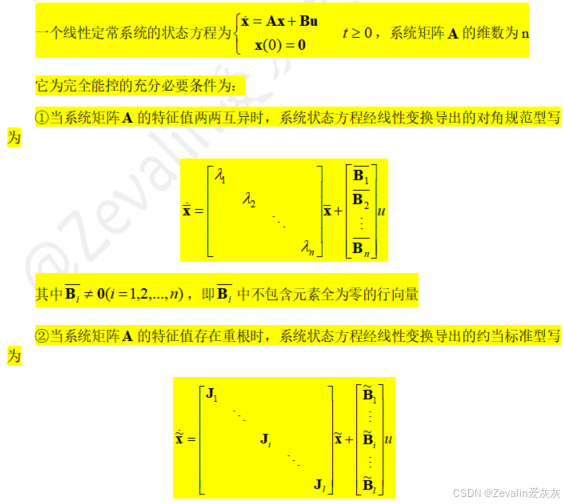
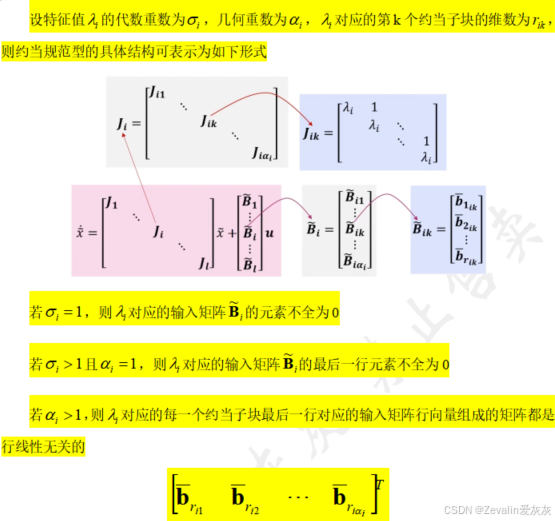
(2)对角规范型判据证明:

(3)约当规范型判据证明:
应用PBH秩判据,可推导出约当规范型完全能控的充要条件,由于一般地表述较为复杂,这里以一个7维系统进行说明



(4)规范型判据的应用举例:




三、线性定常系统的能观性
1、线性定常系统的能观性的定义与描述

2、线性定常系统能观性的判据




3、线性定常系统能观性的判据应用举例

四、线性时变系统的能控性能观性
1、线性时变系统能控性的定义

2、线性时变系统能控性的判据
(1)Gram(格拉姆)矩阵判据:

(2)秩判据:

(3)线性时变系统能控性的判据应用举例:

3、线性时变系统能观性的定义

4、线性时变系统能观性的判据




五、对偶原理
1、对偶系统的定义
(1)线性时变对偶系统:

(2)线性定常对偶系统:

2、线性时变系统的对偶原理
(1)讨论性质------互为对偶的两系统的状态转移矩阵互为转置逆。


(2)对偶原理内容:

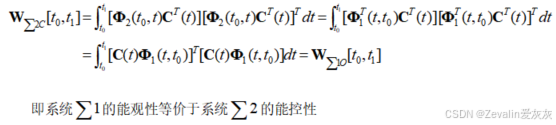
3、线性定常系统的对偶原理
(1)讨论性质------互为对偶的两系统的状态转移矩阵互为转置逆。

(2)对偶原理内容:


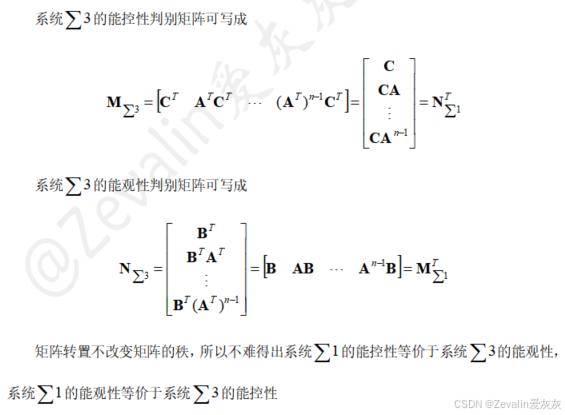
六、状态空间表达式的能控能观标准型
1、能控性与能观性的不变性

2、能控标准I型变换
(1)定理:

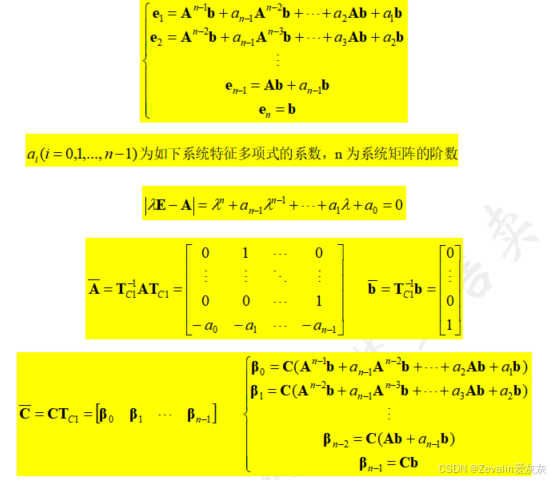
(2)定理证明如下:



(3)举例:

3、能控标准II型变换
(1)定理:


(2)定理证明如下:


(3)举例:

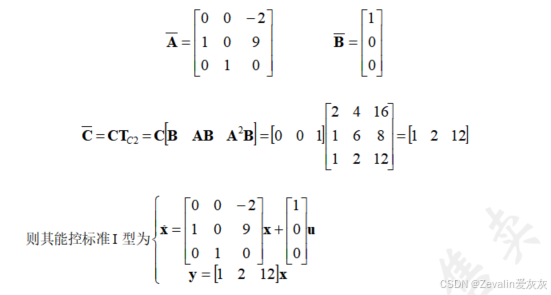
4、能观标准I型变换
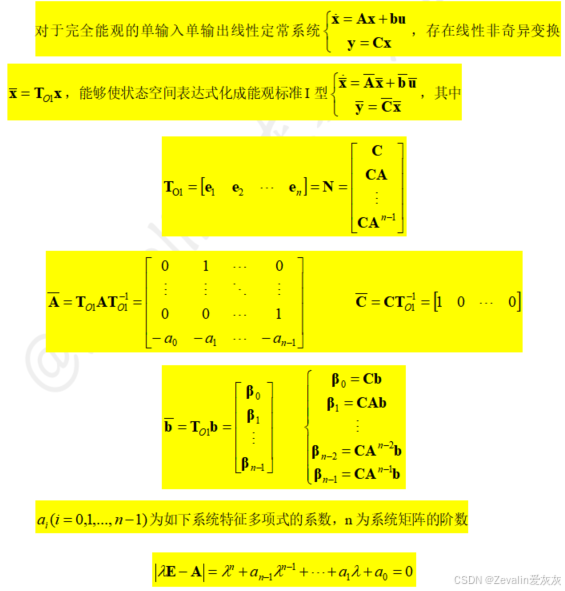
5、能观标准II型变换

七、状态空间表达式的能控能观分解
1、能控性分解
(1)能控性分解的说明:



(2)能控性分解举例:



2、能观性分解
(1)能观性分解的说明:



(2)能观性分解举例:

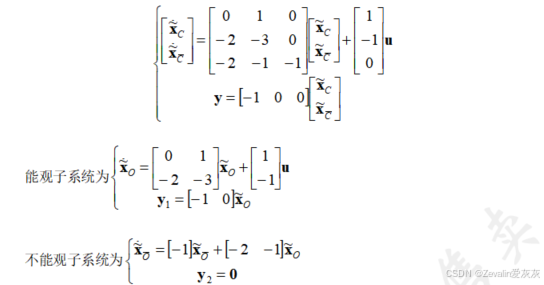
3、能控性和能观性分解
