【系列跟学之——强化学习】基础篇

清蒸鳜鱼2026-01-16 13:43

目录

  • [1 强化学习的概念](#1 强化学习的概念)
  • [2 多臂老虎机](#2 多臂老虎机)
    • [2.1 问题介绍](#2.1 问题介绍)
    • [2.2 ε-贪婪算法（ε-Greedy）](#2.2 ε-贪婪算法（ε-Greedy）)
    • [2.3 上置信界算法（UCB）](#2.3 上置信界算法（UCB）)
    • [2.4 汤普森采样（Thompson Sampling）](#2.4 汤普森采样（Thompson Sampling）)
    • [2.5 关于懊悔的说明](#2.5 关于懊悔的说明)
    • [2.6 算法对比 & 与强化学习的关系](#2.6 算法对比 & 与强化学习的关系)
    • [本部分 所有算法的代码](#本部分 所有算法的代码)
  • [3 马尔可夫决策过程](#3 马尔可夫决策过程)
    • [3.1 马尔可夫过程（MP）](#3.1 马尔可夫过程（MP）)
    • [3.2 马尔可夫奖励过程（MRP）](#3.2 马尔可夫奖励过程（MRP）)
    • [3.3 马尔可夫决策过程（MDP）](#3.3 马尔可夫决策过程（MDP）)
    • [3.4 蒙特卡洛方法](#3.4 蒙特卡洛方法)
    • [3.5 占用度量](#3.5 占用度量)
    • [3.6 最优策略](#3.6 最优策略)
    • 总结1：三种过程的递进关系
    • 总结2：最核心的公式
    • 本部分的所有代码
  • [4 动态规划算法](#4 动态规划算法)
    • [4.1 简介](#4.1 简介)
    • [4.2 悬崖漫步环境](#4.2 悬崖漫步环境)
    • [4.3 策略迭代算法](#4.3 策略迭代算法)
      • [4.3.1 策略评估](#4.3.1 策略评估)
      • [4.3.2 策略提升](#4.3.2 策略提升)
      • [4.3.3 策略迭代流程](#4.3.3 策略迭代流程)
    • [4.4 价值迭代算法](#4.4 价值迭代算法)
    • 本部分的代码
  • [5 时序差分算法](#5 时序差分算法)
    • [5.1 时序差分 vs 蒙特卡洛](#5.1 时序差分 vs 蒙特卡洛)
    • [5.2 Sarsa 算法](#5.2 Sarsa 算法)
    • [5.3 多步 Sarsa 算法](#5.3 多步 Sarsa 算法)
    • [5.4 Q-learning 算法](#5.4 Q-learning 算法)
    • [5.5 本章总结](#5.5 本章总结)
    • 本部分的所有代码
  • [6 Dyan-Q算法](#6 Dyan-Q算法)

学习资料：https://hrl.boyuai.com

1 强化学习的概念

强化学习用智能体（agent）这个概念来表示做决策的机器。相比于有监督学习中的"模型"，强化学习中的"智能体"强调机器不但可以感知周围的环境信息，还可以通过做决策来直接改变这个环境，而不只是给出一些预测信号。

这里，智能体有3种关键要素，即感知、决策和奖励。

强化学习vs监督学习

这是一个非常精准且深刻的定义。为了帮你更好地理解和记忆，我将这段文字总结为核心区别 、形象比喻 和数学本质三个维度：

维度 监督学习 (Supervised Learning) 强化学习 (Reinforcement Learning)
核心目标 拟合数据 (Fitting Data) 探索最优 (Exploring Optimal)
关注点 寻找一个模型 ( f f f) 寻找一个策略 ( π \pi π)
数据视角 给定的 (Given)：数据分布是固定的，不可改变。 产生的 (Generated)：数据分布由智能体的行为决定，是动态变化的。
优化方向 最小化 损失函数的期望 (Error ↓ \downarrow ↓) 最大化 奖励函数的期望 (Reward ↑ \uparrow ↑)
交互方式 被动接收数据（看一眼，学一下）。 主动与环境交互（试一下，看反馈）。

2 多臂老虎机

2.1 问题介绍

场景：面前有一台 K 根拉杆的老虎机，每根拉杆对应不同的奖励概率分布（未知）。目标是在有限次操作内获得尽可能高的累积奖励。

核心挑战：探索与利用的平衡

  • 探索（Exploration）：尝试不同拉杆，了解奖励分布
  • 利用（Exploitation）：选择当前已知最优的拉杆

形式化定义：

  • 动作集合： A = { a 1 , a 2 , . . . , a K } \mathcal{A} = \{a_1, a_2, ..., a_K\} A={a1,a2,...,aK}
  • 奖励分布：拉动拉杆 a k a_k ak 获得的奖励 r r r 服从概率分布 R ( r ∣ a k ) \mathcal{R}(r|a_k) R(r∣ak)
  • 目标：最大化累积奖励 ∑ t = 1 T r t \sum_{t=1}^{T} r_t ∑t=1Trt

期望奖励与最优期望：

  • 动作 a a a 的期望奖励： Q ( a ) = E [ r ∣ a ] Q(a) = \mathbb{E}[r|a] Q(a)=E[r∣a]
  • 最优期望奖励： Q ∗ = max ⁡ a ∈ A Q ( a ) Q^* = \max_{a \in \mathcal{A}} Q(a) Q∗=maxa∈AQ(a)

懊悔与累积懊悔：

  • 单步懊悔： R ( a ) = Q ∗ − Q ( a ) R(a) = Q^* - Q(a) R(a)=Q∗−Q(a)
  • 累积懊悔： σ R = ∑ t = 1 T R ( a t ) = ∑ t = 1 T ( Q ∗ − Q ( a t ) ) \sigma_R = \sum_{t=1}^{T} R(a_t) = \sum_{t=1}^{T} (Q^* - Q(a_t)) σR=∑t=1TR(at)=∑t=1T(Q∗−Q(at))

目标"最大化累积奖励"等价于"最小化累积懊悔"。

原因：
累积奖励 ：
∑ t = 1 T Q ( a t ) \sum_{t=1}^{T} Q(a_t) t=1∑TQ(at)
累积懊悔 ：
σ R = ∑ t = 1 T ( Q ∗ − Q ( a t ) ) = T ⋅ Q ∗ − ∑ t = 1 T Q ( a t ) \sigma_R = \sum_{t=1}^{T} (Q^* - Q(a_t)) = T \cdot Q^* - \sum_{t=1}^{T} Q(a_t) σR=t=1∑T(Q∗−Q(at))=T⋅Q∗−t=1∑TQ(at)

因为 T ⋅ Q ∗ T \cdot Q^* T⋅Q∗ 是一个常数（总步数 × 最优期望奖励），所以：
σ R = T ⋅ Q ∗ ⏟ 常数 − ∑ t = 1 T Q ( a t ) ⏟ 累积奖励 \sigma_R = \underbrace{T \cdot Q^*}{\text{常数}} - \underbrace{\sum{t=1}^{T} Q(a_t)}_{\text{累积奖励}} σR=常数 T⋅Q∗−累积奖励 t=1∑TQ(at)

当累积奖励越大时，累积懊悔就越小；当累积奖励越小时，累积懊悔就越大。

所以最大化累积奖励 和最小化累积懊悔是完全等价的目标。
为什么用懊悔而不是奖励？

用懊悔来衡量有一个好处：它能直观反映算法和"最优策略"之间的差距。如果累积懊悔增长慢（比如对数增长），说明算法很快就能找到最优拉杆并持续利用它。

期望奖励估计的增量更新公式：

Q k = Q k − 1 + 1 k ( r k − Q k − 1 ) Q_k = Q_{k-1} + \frac{1}{k}(r_k - Q_{k-1}) Qk=Qk−1+k1(rk−Qk−1)

推导过程：

Q k = 1 k ∑ i = 1 k r i = 1 k ( r k + ∑ i = 1 k − 1 r i ) = 1 k ( r k + ( k − 1 ) Q k − 1 ) = 1 k r k + k − 1 k Q k − 1 = 1 k r k + Q k − 1 − 1 k Q k − 1 = Q k − 1 + 1 k ( r k − Q k − 1 ) \begin{aligned} Q_k &= \frac{1}{k} \sum_{i=1}^{k} r_i \\ &= \frac{1}{k} \left( r_k + \sum_{i=1}^{k-1} r_i \right) \\ &= \frac{1}{k} \left( r_k + (k-1) Q_{k-1} \right) \\ &= \frac{1}{k} r_k + \frac{k-1}{k} Q_{k-1} \\ &= \frac{1}{k} r_k + Q_{k-1} - \frac{1}{k} Q_{k-1} \\ &= Q_{k-1} + \frac{1}{k}(r_k - Q_{k-1}) \end{aligned} Qk=k1i=1∑kri=k1(rk+i=1∑k−1ri)=k1(rk+(k−1)Qk−1)=k1rk+kk−1Qk−1=k1rk+Qk−1−k1Qk−1=Qk−1+k1(rk−Qk−1)

这样每次更新只需 O ( 1 ) O(1) O(1) 的时间和空间复杂度。

2.2 ε-贪婪算法（ε-Greedy）

思想：以小概率探索，大概率利用

策略：

a t = { arg ⁡ max ⁡ a Q ^ ( a ) 以概率 1 − ϵ （利用） 随机选择 以概率 ϵ （探索） a_t = \begin{cases} \arg\max_a \hat{Q}(a) & \text{以概率 } 1-\epsilon \text{（利用）} \\ \text{随机选择} & \text{以概率 } \epsilon \text{（探索）} \end{cases} at={argmaxaQ^(a)随机选择以概率 1−ϵ（利用）以概率 ϵ（探索）

改进：ε 衰减

ϵ t = 1 t \epsilon_t = \frac{1}{t} ϵt=t1

性能：

  • 固定 ε：累积懊悔线性增长 O ( T ) O(T) O(T)
  • ε 衰减：累积懊悔次线性增长 O ( log ⁡ T ) O(\log T) O(logT)

懊悔分析：

随机探索的平均懊悔为 Δ ˉ = 1 K ∑ k = 1 K ( Q ∗ − Q ( a k ) ) \bar{\Delta} = \frac{1}{K} \sum_{k=1}^{K} (Q^* - Q(a_k)) Δˉ=K1∑k=1K(Q∗−Q(ak))

  • 固定 ε ：每步期望懊悔为 ϵ ⋅ Δ ˉ \epsilon \cdot \bar{\Delta} ϵ⋅Δˉ，T 步累积懊悔为 T ⋅ ϵ ⋅ Δ ˉ T \cdot \epsilon \cdot \bar{\Delta} T⋅ϵ⋅Δˉ，呈线性增长
  • ε 衰减 （ ϵ t = 1 / t \epsilon_t = 1/t ϵt=1/t）：累积懊悔为 Δ ˉ ∑ t = 1 T 1 t ≈ Δ ˉ ln ⁡ T \bar{\Delta} \sum_{t=1}^{T} \frac{1}{t} \approx \bar{\Delta} \ln T Δˉ∑t=1Tt1≈ΔˉlnT，呈对数增长

其中 ∑ t = 1 T 1 t ≈ ln ⁡ T \sum_{t=1}^{T} \frac{1}{t} \approx \ln T ∑t=1Tt1≈lnT 是调和级数的近似（由积分 ∫ 1 T 1 x d x = ln ⁡ T \int_1^T \frac{1}{x}dx = \ln T ∫1Tx1dx=lnT 得到）。

2.3 上置信界算法（UCB）

思想：不确定性越大，越值得探索（"乐观面对不确定性"）

策略：

a t = arg ⁡ max ⁡ a [ Q ^ ( a ) + c ln ⁡ t 2 N ( a ) ] a_t = \arg\max_a \left[ \hat{Q}(a) + c\sqrt{\frac{\ln t}{2N(a)}} \right] at=argamax[Q^(a)+c2N(a)lnt ]

其中：

  • Q ^ ( a ) \hat{Q}(a) Q^(a)：动作 a a a 的期望奖励估计值
  • N ( a ) N(a) N(a)：动作 a a a 被选择的次数
  • t t t：当前总步数
  • c c c：探索系数

直观理解：

  • 被选次数少 → 不确定性项大 → UCB 值高 → 更可能被选中探索
  • 被选次数多 → 不确定性项小 → 主要看期望估计值

性能 ：累积懊悔对数增长 O ( log ⁡ T ) O(\log T) O(logT)

懊悔分析 ：不确定性项 ln ⁡ t N ( a ) \sqrt{\frac{\ln t}{N(a)}} N(a)lnt 随选择次数增加而减小，次优拉杆被选次数有上界约 O ( ln ⁡ T ) O(\ln T) O(lnT)，总懊悔为 O ( log ⁡ T ) O(\log T) O(logT)。

2.4 汤普森采样（Thompson Sampling）

思想：用概率分布描述不确定性，通过采样做决策

策略（针对伯努利老虎机）：

  1. 对每个动作 a a a，维护成功次数 α a \alpha_a αa 和失败次数 β a \beta_a βa
  2. 从每个动作的 Beta 分布中采样： θ a ∼ Beta ( α a + 1 , β a + 1 ) \theta_a \sim \text{Beta}(\alpha_a + 1, \beta_a + 1) θa∼Beta(αa+1,βa+1)
  3. 选择采样值最大的动作： a t = arg ⁡ max ⁡ a θ a a_t = \arg\max_a \theta_a at=argmaxaθa
  4. 更新：若获奖则 α a ← α a + 1 \alpha_a \leftarrow \alpha_a + 1 αa←αa+1，否则 β a ← β a + 1 \beta_a \leftarrow \beta_a + 1 βa←βa+1

直观理解：

  • 选择次数少 → Beta 分布宽 → 采样值波动大 → 有机会采样到高值被探索
  • 选择次数多 → Beta 分布窄 → 采样值稳定 → 收敛到真实期望

性能 ：累积懊悔对数增长 O ( log ⁡ T ) O(\log T) O(logT)

懊悔分析 ：随着采样次数增加，Beta 分布逐渐集中在真实概率附近，次优拉杆采样值超过最优拉杆的概率越来越小，总懊悔为 O ( log ⁡ T ) O(\log T) O(logT)。

2.5 关于懊悔的说明

Q ∗ Q^* Q∗ 是真实的最优期望奖励 ，由环境决定，固定不变但未知。懊悔是理论分析工具，不是算法运行时需要计算的：

场景 是否知道 Q ∗ Q^* Q∗ 懊悔的作用
理论分析 假设存在 证明算法性能上界
实验仿真 人为设定，已知 画图比较算法
真实应用 不知道 不需要算，直接跑算法

算法本身只依赖估计值 Q ^ ( a ) \hat{Q}(a) Q^(a)，不需要知道 Q ∗ Q^* Q∗。

2.6 算法对比 & 与强化学习的关系

算法 探索机制 累积懊悔增长
ε-贪婪（固定 ε） 随机探索 线性 O ( T ) O(T) O(T)
ε-贪婪（ε 衰减） 随机探索，逐渐减少 对数 O ( log ⁡ T ) O(\log T) O(logT)
UCB 基于不确定性上界 对数 O ( log ⁡ T ) O(\log T) O(logT)
Thompson Sampling 基于概率分布采样 对数 O ( log ⁡ T ) O(\log T) O(logT)

累积懊悔的"复杂度"其实不是时间复杂度

这里的 O ( log ⁡ T ) O(\log T) O(logT) 或 O ( T ) O(T) O(T) 描述的是累积懊悔随步数 T 增长的速度 ，不是计算需要多少时间。

举例：

假设 Δ ˉ = 0.1 \bar{\Delta} = 0.1 Δˉ=0.1（平均每次选错的损失）

步数 T 固定 ε=0.1 的懊悔 O ( T ) O(T) O(T) ε 衰减的懊悔 O ( log ⁡ T ) O(\log T) O(logT)
10 10 × 0.1 × 0.1 = 0.1 10 \times 0.1 \times 0.1 = 0.1 10×0.1×0.1=0.1 0.1 × ln ⁡ 10 ≈ 0.23 0.1 \times \ln 10 \approx 0.23 0.1×ln10≈0.23
100 100 × 0.1 × 0.1 = 1 100 \times 0.1 \times 0.1 = 1 100×0.1×0.1=1 0.1 × ln ⁡ 100 ≈ 0.46 0.1 \times \ln 100 \approx 0.46 0.1×ln100≈0.46
1000 1000 × 0.1 × 0.1 = 10 1000 \times 0.1 \times 0.1 = 10 1000×0.1×0.1=10 0.1 × ln ⁡ 1000 ≈ 0.69 0.1 \times \ln 1000 \approx 0.69 0.1×ln1000≈0.69
10000 10000 × 0.1 × 0.1 = 100 10000 \times 0.1 \times 0.1 = 100 10000×0.1×0.1=100 0.1 × ln ⁡ 10000 ≈ 0.92 0.1 \times \ln 10000 \approx 0.92 0.1×ln10000≈0.92

因此 O ( T ) O(T) O(T)：步数增加 10 倍，懊悔也增加约 10 倍（线性）， O ( log ⁡ T ) O(\log T) O(logT)：步数增加 10 倍，懊悔只增加一点点（对数）

多臂老虎机是无状态的强化学习 ------每次交互不会改变环境。强化学习在此基础上引入状态，形成马尔可夫决策过程（MDP）。

本部分 所有算法的代码

python 复制代码 
# 导入需要使用的库,其中numpy是支持数组和矩阵运算的科学计算库,而matplotlib是绘图库
import numpy as np
import matplotlib.pyplot as plt


class BernoulliBandit:
    """ 伯努利多臂老虎机,输入K表示拉杆个数 """
    def __init__(self, K):
        self.probs = np.random.uniform(size=K)  # 随机生成K个0～1的数,作为拉动每根拉杆的获奖
        print("各拉杆的获奖概率分别为:", np.round(self.probs, 4))
        # 概率
        self.best_idx = np.argmax(self.probs)  # 获奖概率最大的拉杆
        self.best_prob = self.probs[self.best_idx]  # 最大的获奖概率
        self.K = K

    def step(self, k):
        # 当玩家选择了k号拉杆后,根据拉动该老虎机的k号拉杆获得奖励的概率返回1（获奖）或0（未
        # 获奖）
        if np.random.rand() < self.probs[k]:
            print("拉动了%d号拉杆,获得奖励1" % k)
            return 1
        else:
            return 0

class Solver:
    """ 多臂老虎机算法基本框架 """
    def __init__(self, bandit):
        self.bandit = bandit
        self.counts = np.zeros(self.bandit.K)  # 每根拉杆的尝试次数
        self.regret = 0.  # 当前步的累积懊悔
        self.actions = []  # 维护一个列表,记录每一步的动作
        self.regrets = []  # 维护一个列表,记录每一步的累积懊悔

    def update_regret(self, k):
        # 计算累积懊悔并保存,k为本次动作选择的拉杆的编号
        self.regret += self.bandit.best_prob - self.bandit.probs[k]
        self.regrets.append(self.regret)

    def run_one_step(self):
        # 返回当前动作选择哪一根拉杆,由每个具体的策略实现
        raise NotImplementedError

    def run(self, num_steps):
        # 运行一定次数,num_steps为总运行次数
        for _ in range(num_steps):
            k = self.run_one_step()
            self.counts[k] += 1
            self.actions.append(k)
            self.update_regret(k)

class EpsilonGreedy(Solver):
    """ epsilon贪婪算法,继承Solver类 """
    def __init__(self, bandit, epsilon=0.01, init_prob=1.0):
        super(EpsilonGreedy, self).__init__(bandit)
        self.epsilon = epsilon
        #初始化拉动所有拉杆的期望奖励估值
        self.estimates = np.array([init_prob] * self.bandit.K)

    def run_one_step(self):
        if np.random.random() < self.epsilon:
            k = np.random.randint(0, self.bandit.K)  # 随机选择一根拉杆
        else:
            k = np.argmax(self.estimates)  # 选择期望奖励估值最大的拉杆
        r = self.bandit.step(k)  # 得到本次动作的奖励
        self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
        return k

class DecayingEpsilonGreedy(Solver):
    """ epsilon值随时间衰减的epsilon-贪婪算法,继承Solver类 """
    def __init__(self, bandit, init_prob=1.0):
        super(DecayingEpsilonGreedy, self).__init__(bandit)
        self.estimates = np.array([init_prob] * self.bandit.K)
        self.total_count = 0

    def run_one_step(self):
        self.total_count += 1
        
        epsilon = 1 / (1 + 0.001 * self.total_count)  # 改用更慢的衰减方式，而不是1/t
        if np.random.random() < epsilon:
            k = np.random.randint(0, self.bandit.K)
        else:
            k = np.argmax(self.estimates)

        r = self.bandit.step(k)
        self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
        return k

class UCB(Solver):
    """ UCB算法,继承Solver类 """
    def __init__(self, bandit, coef, init_prob=1.0):
        super(UCB, self).__init__(bandit)
        self.total_count = 0
        self.estimates = np.array([init_prob] * self.bandit.K)
        self.coef = coef

    def run_one_step(self):
        self.total_count += 1
        ucb = self.estimates + self.coef * np.sqrt(
            np.log(self.total_count) / (2 * (self.counts + 1)))  # 计算上置信界
        k = np.argmax(ucb)  # 选出上置信界最大的拉杆
        r = self.bandit.step(k)
        self.estimates[k] += 1. / (self.counts[k] + 1) * (r - self.estimates[k])
        return k

class ThompsonSampling(Solver):
    """ 汤普森采样算法,继承Solver类 """
    def __init__(self, bandit):
        super(ThompsonSampling, self).__init__(bandit)
        self._a = np.ones(self.bandit.K)  # 列表,表示每根拉杆奖励为1的次数
        self._b = np.ones(self.bandit.K)  # 列表,表示每根拉杆奖励为0的次数

    def run_one_step(self):
        samples = np.random.beta(self._a, self._b)  # 按照Beta分布采样一组奖励样本
        k = np.argmax(samples)  # 选出采样奖励最大的拉杆
        r = self.bandit.step(k)

        self._a[k] += r  # 更新Beta分布的第一个参数
        self._b[k] += (1 - r)  # 更新Beta分布的第二个参数
        return k

# ==============================
def plot_results(solvers, solver_names):
    """生成累积懊悔随时间变化的图像。输入solvers是一个列表,列表中的每个元素是一种特定的策略。
    而solver_names也是一个列表,存储每个策略的名称"""
    for idx, solver in enumerate(solvers):
        time_list = range(len(solver.regrets))
        plt.plot(time_list, solver.regrets, label=solver_names[idx])
    plt.xlabel('Time steps')
    plt.ylabel('Cumulative regrets')
    plt.title('%d-armed bandit' % solvers[0].bandit.K)
    plt.legend()
    plt.show()

# ===============主函数==================
np.random.seed(1)
K = 10
bandit_10_arm = BernoulliBandit(K)
print("随机生成了一个%d臂伯努利老虎机" % K)
print("获奖概率最大的拉杆为%d号,其获奖概率为%.4f" %
      (bandit_10_arm.best_idx, bandit_10_arm.best_prob))
print('-' * 50)

# 运行epsilon-贪婪算法
epsilon_greedy_solver = EpsilonGreedy(bandit_10_arm, epsilon=0.01)
epsilon_greedy_solver.run(5000)
print('epsilon-贪婪算法的累积懊悔为：', epsilon_greedy_solver.regret)
plot_results([epsilon_greedy_solver], ["EpsilonGreedy"])
print('-' * 50)

# 运行不同epsilon值的epsilon-贪婪算法进行对比
epsilons = [1e-4, 0.01, 0.1, 0.25, 0.5]
epsilon_greedy_solver_list = [
    EpsilonGreedy(bandit_10_arm, epsilon=e) for e in epsilons
]
epsilon_greedy_solver_names = ["epsilon={}".format(e) for e in epsilons]
for solver in epsilon_greedy_solver_list:
    solver.run(5000)

# plot_results(epsilon_greedy_solver_list, epsilon_greedy_solver_names)

# 运行epsilon值衰减的epsilon-贪婪算法
decaying_epsilon_greedy_solver = DecayingEpsilonGreedy(bandit_10_arm)
decaying_epsilon_greedy_solver.run(5000)
print('epsilon值衰减的贪婪算法的累积懊悔为：', decaying_epsilon_greedy_solver.regret)
plot_results([decaying_epsilon_greedy_solver], ["DecayingEpsilonGreedy"])
# 在运行结束后，检查算法是否找到了最优拉杆
print("各拉杆被选择的次数:", decaying_epsilon_greedy_solver.counts)
print("最优拉杆编号:", bandit_10_arm.best_idx)
print("各拉杆的期望估计值:", np.round(decaying_epsilon_greedy_solver.estimates, 4))

# 运行上置信界算法
coef = 1  # 控制不确定性比重的系数
UCB_solver = UCB(bandit_10_arm, coef)
UCB_solver.run(5000)
print('上置信界算法的累积懊悔为：', UCB_solver.regret)
plot_results([UCB_solver], ["UCB"])

# 运行汤普森采样算法
thompson_sampling_solver = ThompsonSampling(bandit_10_arm)
thompson_sampling_solver.run(5000)
print('汤普森采样算法的累积懊悔为：', thompson_sampling_solver.regret)
plot_results([thompson_sampling_solver], ["ThompsonSampling"])

3 马尔可夫决策过程

3.1 马尔可夫过程（MP）

组成元素

符号 含义 例子
S S S 状态集合 { s 1 , s 2 , s 3 , s 4 , s 5 , s 6 } \{s_1, s_2, s_3, s_4, s_5, s_6\} {s1,s2,s3,s4,s5,s6}
P P P 状态转移矩阵 P ( s j ∣ s i ) P(s_j | s_i) P(sj∣si) = 从 s i s_i si 到 s j s_j sj 的概率

核心性质（马尔可夫性质）：下一状态只取决于当前状态，与历史无关。无公式，只需理解概念。

3.2 马尔可夫奖励过程（MRP）

组成元素

符号 含义 例子
S S S 状态集合 { s 1 , s 2 , . . . } \{s_1, s_2, ...\} {s1,s2,...}
P P P 状态转移矩阵 P ( s ′ ∣ s ) P(s' | s) P(s′∣s)
R ( s ) R(s) R(s) 奖励函数（在节点上） R ( s 4 ) = 10 R(s_4) = 10 R(s4)=10
γ \gamma γ 折扣因子 0.5 0.5 0.5
G t G_t Gt 回报（从 t t t 时刻开始往未来的累计奖励） 一条轨迹的总收益
V ( s ) V(s) V(s) 价值函数（回报的期望） 从 s s s 出发平均能拿多少

R、G、V 的关系

符号 名称 一句话解释
R R R 奖励 这一步拿了多少
G G G 回报 这一局往后总共能拿多少
V V V 价值 平均每局能拿多少
复制代码 
R（单步奖励）
    ↓ 累加（带折扣）
G（一条轨迹的总回报）
    ↓ 求期望
V（平均回报）

核心公式

回报的定义：
G t = R t + γ R t + 1 + γ 2 R t + 2 + ⋯ G_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots Gt=Rt+γRt+1+γ2Rt+2+⋯

回报的递归形式：
G t = R t + γ G t + 1 G_t = R_t + \gamma G_{t+1} Gt=Rt+γGt+1

价值函数：
V ( s ) = E [ G t ∣ S t = s ] V(s) = \mathbb{E}[G_t | S_t = s] V(s)=E[Gt∣St=s]

贝尔曼方程：
V ( s ) = R ( s ) + γ ∑ s ′ P ( s ′ ∣ s ) V ( s ′ ) V(s) = R(s) + \gamma \sum_{s'} P(s'|s) V(s') V(s)=R(s)+γs′∑P(s′∣s)V(s′)

矩阵形式：
V = R + γ P V \mathcal{V} = \mathcal{R} + \gamma \mathcal{P} \mathcal{V} V=R+γPV

解析解：
V = ( I − γ P ) − 1 R \mathcal{V} = (\mathbf{I} - \gamma \mathcal{P})^{-1} \mathcal{R} V=(I−γP)−1R

3.3 马尔可夫决策过程（MDP）

组成元素

符号 含义 例子
S S S 状态集合 { s 1 , s 2 , s 3 , s 4 , s 5 } \{s_1, s_2, s_3, s_4, s_5\} {s1,s2,s3,s4,s5}
A A A 动作集合 { 保持 , 前往 , . . . } \{\text{保持}, \text{前往}, ...\} {保持,前往,...}
P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a) 状态转移函数 在 s s s 选 a a a 后到 s ′ s' s′ 的概率
R ( s , a ) R(s,a) R(s,a) 奖励函数（在边上） R ( s 4 , 前往 s 5 ) = 10 R(s_4, \text{前往}s_5) = 10 R(s4,前往s5)=10
γ \gamma γ 折扣因子 0.5 0.5 0.5
π ( a ∣ s ) \pi(a|s) π(a∣s) 策略（在状态 s s s 选动作 a a a 的概率） π ( 前往 s 5 ∣ s 4 ) = 0.5 \pi(\text{前往}s_5 | s_4) = 0.5 π(前往s5∣s4)=0.5
G t G_t Gt 回报 同 MRP
V π ( s ) V^\pi(s) Vπ(s) 状态价值函数 用策略 π \pi π，从 s s s 出发的期望回报
Q π ( s , a ) Q^\pi(s,a) Qπ(s,a) 动作价值函数 用策略 π \pi π，在 s s s 选 a a a 的期望回报

MRP vs MDP 对比

MRP MDP
奖励在哪 节点上 R ( s ) R(s) R(s) 边上 R ( s , a ) R(s,a) R(s,a)
转移概率 P ( s ′ ∣ s ) P(s'|s) P(s′∣s) P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a)
有无动作 无 有
价值函数 V ( s ) V(s) V(s) V π ( s ) V^\pi(s) Vπ(s)（依赖策略）

V 和 Q 的区别

V π ( s ) V^\pi(s) Vπ(s) Q π ( s , a ) Q^\pi(s,a) Qπ(s,a)
问的问题 在状态 s s s，未来能拿多少？ 在状态 s s s 选动作 a a a，未来能拿多少？
输入 状态 s s s 状态 s s s + 动作 a a a

核心公式

状态价值函数：
V π ( s ) = E π [ G t ∣ S t = s ] V^\pi(s) = \mathbb{E}_\pi[G_t | S_t = s] Vπ(s)=Eπ[Gt∣St=s]

动作价值函数：
Q π ( s , a ) = E π [ G t ∣ S t = s , A t = a ] Q^\pi(s,a) = \mathbb{E}_\pi[G_t | S_t = s, A_t = a] Qπ(s,a)=Eπ[Gt∣St=s,At=a]

V 和 Q 的关系：
V π ( s ) = ∑ a π ( a ∣ s ) ⋅ Q π ( s , a ) V^\pi(s) = \sum_a \pi(a|s) \cdot Q^\pi(s,a) Vπ(s)=a∑π(a∣s)⋅Qπ(s,a)

Q π ( s , a ) = R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V π ( s ′ ) Q^\pi(s,a) = R(s,a) + \gamma \sum_{s'} P(s'|s,a) V^\pi(s') Qπ(s,a)=R(s,a)+γs′∑P(s′∣s,a)Vπ(s′)

贝尔曼期望方程：
V π ( s ) = ∑ a π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V π ( s ′ ) ] V^\pi(s) = \sum_a \pi(a|s) \left[ R(s,a) + \gamma \sum_{s'} P(s'|s,a) V^\pi(s') \right] Vπ(s)=a∑π(a∣s)[R(s,a)+γs′∑P(s′∣s,a)Vπ(s′)]

MDP → MRP 转化（边缘化）

奖励边缘化（边上 → 节点上）：
R M R P ( s ) = ∑ a π ( a ∣ s ) ⋅ R ( s , a ) R_{MRP}(s) = \sum_a \pi(a|s) \cdot R(s,a) RMRP(s)=a∑π(a∣s)⋅R(s,a)

转移概率边缘化：
P M R P ( s ′ ∣ s ) = ∑ a π ( a ∣ s ) ⋅ P ( s ′ ∣ s , a ) P_{MRP}(s'|s) = \sum_a \pi(a|s) \cdot P(s'|s,a) PMRP(s′∣s)=a∑π(a∣s)⋅P(s′∣s,a)

3.4 蒙特卡洛方法

核心思想：不用公式推导，直接做实验求平均。

需要的变量

符号 含义
N ( s ) N(s) N(s) 状态 s s s 被访问的次数
G G G 回报

核心公式

价值估计：
V ( s ) ≈ 1 N ( s ) ∑ i = 1 N ( s ) G i ( s ) V(s) \approx \frac{1}{N(s)} \sum_{i=1}^{N(s)} G_i(s) V(s)≈N(s)1i=1∑N(s)Gi(s)

增量更新：
V ( s ) ← V ( s ) + 1 N ( s ) ( G − V ( s ) ) V(s) \leftarrow V(s) + \frac{1}{N(s)}(G - V(s)) V(s)←V(s)+N(s)1(G−V(s))

算法步骤

复制代码 
1. 采样很多条轨迹
2. 对每条轨迹，从后往前计算每个状态的回报 G
   （因为 G_t = R_t + γG_{t+1}，必须先知道后面的）
3. 更新该状态的价值（取平均）

和解析解对比

解析解 蒙特卡洛
需要知道 转移概率 P、奖励 R 不需要！只要能玩游戏
计算方式 矩阵求逆 采样 + 求平均
结果 精确 近似（采样越多越准）

3.5 占用度量

核心概念

符号 含义 一句话解释
ν π ( s ) \nu^\pi(s) νπ(s) 状态访问分布 用策略 π \pi π 访问状态 s s s 的频率
ρ π ( s , a ) \rho^\pi(s,a) ρπ(s,a) 占用度量 用策略 π \pi π 访问 ( s , a ) (s,a) (s,a) 的频率

核心公式

ρ π ( s , a ) = ν π ( s ) ⋅ π ( a ∣ s ) \rho^\pi(s,a) = \nu^\pi(s) \cdot \pi(a|s) ρπ(s,a)=νπ(s)⋅π(a∣s)

ν π ( s ) = ∑ a ρ π ( s , a ) \nu^\pi(s) = \sum_a \rho^\pi(s,a) νπ(s)=a∑ρπ(s,a)

直观理解 ：玩 1000 步游戏，统计 ν π ( s 4 ) = 0.1 \nu^\pi(s_4) = 0.1 νπ(s4)=0.1 表示 10% 的时间在状态 s 4 s_4 s4， ρ π ( s 4 , 前往 s 5 ) = 0.05 \rho^\pi(s_4, \text{前往}s_5) = 0.05 ρπ(s4,前往s5)=0.05 表示 5% 的时间在" s 4 s_4 s4 选前往 s 5 s_5 s5"。

为什么需要？ 策略告诉你"怎么选"，占用度量告诉你"实际会在哪里花时间"。

3.6 最优策略

核心概念

符号 含义
V ∗ ( s ) V^*(s) V∗(s) 最优状态价值：所有策略中最大的 V V V
Q ∗ ( s , a ) Q^*(s,a) Q∗(s,a) 最优动作价值：所有策略中最大的 Q Q Q
π ∗ \pi^* π∗ 最优策略：能达到最优价值的策略

核心公式

最优价值定义：
V ∗ ( s ) = max ⁡ π V π ( s ) V^*(s) = \max_\pi V^\pi(s) V∗(s)=πmaxVπ(s)
Q ∗ ( s , a ) = max ⁡ π Q π ( s , a ) Q^*(s,a) = \max_\pi Q^\pi(s,a) Q∗(s,a)=πmaxQπ(s,a)

最优策略：
π ∗ ( s ) = arg ⁡ max ⁡ a Q ∗ ( s , a ) \pi^*(s) = \arg\max_a Q^*(s,a) π∗(s)=argamaxQ∗(s,a)

贝尔曼最优方程：
V ∗ ( s ) = max ⁡ a [ R ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ∗ ( s ′ ) ] V^*(s) = \max_a \left[ R(s,a) + \gamma \sum_{s'} P(s'|s,a) V^*(s') \right] V∗(s)=amax[R(s,a)+γs′∑P(s′∣s,a)V∗(s′)]

贝尔曼期望方程 vs 贝尔曼最优方程

贝尔曼期望方程 贝尔曼最优方程
对动作 ∑ a π ( a ∣ s ) [ ⋯   ] \sum_a \pi(a|s)[\cdots] ∑aπ(a∣s)[⋯]（按策略加权） max ⁡ a [ ⋯   ] \max_a [\cdots] maxa[⋯]（选最好的）
求的是 某个策略的价值 最优价值

总结1：三种过程的递进关系

复制代码 
马尔可夫过程 (MP)：S, P
        ↓ + 奖励 R、折扣 γ
马尔可夫奖励过程 (MRP)：S, P, R, γ
        ↓ + 动作 A、策略 π
马尔可夫决策过程 (MDP)：S, A, P, R, γ, π

总结2：最核心的公式

名称 公式 一句话解释
回报 G t = R t + γ G t + 1 G_t = R_t + \gamma G_{t+1} Gt=Rt+γGt+1 当前奖励 + 折扣×未来回报
MRP贝尔曼 V ( s ) = R ( s ) + γ ∑ s ′ P ( s ′ ∣ s ) V ( s ′ ) V(s) = R(s) + \gamma \sum_{s'} P(s'|s) V(s') V(s)=R(s)+γ∑s′P(s′∣s)V(s′) 价值 = 即时奖励 + 折扣×下一状态价值期望
V和Q关系 V π ( s ) = ∑ a π ( a ∣ s ) Q π ( s , a ) V^\pi(s) = \sum_a \pi(a|s) Q^\pi(s,a) Vπ(s)=∑aπ(a∣s)Qπ(s,a) 状态价值 = 动作价值的加权平均
MDP贝尔曼 V π ( s ) = ∑ a π ( a ∣ s ) [ R ( s , a ) + γ ∑ s ′ P V π ( s ′ ) ] V^\pi(s) = \sum_a \pi(a|s)[R(s,a) + \gamma \sum_{s'} P V^\pi(s')] Vπ(s)=∑aπ(a∣s)[R(s,a)+γ∑s′PVπ(s′)] 多了动作选择的加权
最优贝尔曼 V ∗ ( s ) = max ⁡ a [ R ( s , a ) + γ ∑ s ′ P V ∗ ( s ′ ) ] V^*(s) = \max_a [R(s,a) + \gamma \sum_{s'} P V^*(s')] V∗(s)=maxa[R(s,a)+γ∑s′PV∗(s′)] 把加权平均换成取最大

本部分的所有代码

python 复制代码 
import numpy as np
np.random.seed(0)

# =============================================================================
# 3.3 马尔可夫奖励过程 (MRP)
# =============================================================================

# MRP的状态转移矩阵 (6个状态: s1, s2, s3, s4, s5, s6)
P_mrp = [
    [0.9, 0.1, 0.0, 0.0, 0.0, 0.0],  # s1
    [0.5, 0.0, 0.5, 0.0, 0.0, 0.0],  # s2
    [0.0, 0.0, 0.0, 0.6, 0.0, 0.4],  # s3
    [0.0, 0.0, 0.0, 0.0, 0.3, 0.7],  # s4
    [0.0, 0.2, 0.3, 0.5, 0.0, 0.0],  # s5
    [0.0, 0.0, 0.0, 0.0, 0.0, 1.0],  # s6 (终止状态)
]
P_mrp = np.array(P_mrp)

# MRP的奖励函数 (进入每个状态的奖励)
rewards_mrp = [-1, -2, -2, 10, 1, 0]

# 折扣因子
gamma = 0.5


# -----------------------------------------------------------------------------
# 3.3.1 计算回报 (Return)
# -----------------------------------------------------------------------------
def compute_return(start_index, chain, gamma):
    """
    计算一条轨迹的回报
    start_index: 从轨迹的哪个位置开始计算
    chain: 状态序列，如 [1, 2, 3, 6] 表示 s1 -> s2 -> s3 -> s6
    gamma: 折扣因子
    """
    G = 0
    for i in reversed(range(start_index, len(chain))):
        G = gamma * G + rewards_mrp[chain[i] - 1]
    return G


# 示例：计算轨迹 s1 -> s2 -> s3 -> s6 的回报
chain = [1, 2, 3, 6]
start_index = 0
G = compute_return(start_index, chain, gamma)
print("=" * 60)
print("3.3.1 回报计算")
print("=" * 60)
print(f"轨迹: {chain}")
print(f"根据本序列计算得到回报为：{G}")


# -----------------------------------------------------------------------------
# 3.3.2 价值函数 - 解析解
# -----------------------------------------------------------------------------
def compute(P, rewards, gamma, states_num):
    """
    利用贝尔曼方程的矩阵形式计算解析解
    V = (I - γP)^(-1) * R
    """
    rewards = np.array(rewards).reshape((-1, 1))
    value = np.dot(np.linalg.inv(np.eye(states_num, states_num) - gamma * P),
                   rewards)
    return value


# 计算MRP中每个状态的价值
V_mrp = compute(P_mrp, rewards_mrp, gamma, 6)
print("\n" + "=" * 60)
print("3.3.2 MRP价值函数（解析解）")
print("=" * 60)
print("MRP中每个状态价值分别为：")
print(V_mrp)


# =============================================================================
# 3.4 马尔可夫决策过程 (MDP)
# =============================================================================

print("\n" + "=" * 60)
print("3.4 马尔可夫决策过程 (MDP)")
print("=" * 60)

# 状态集合
S = ["s1", "s2", "s3", "s4", "s5"]

# 动作集合
A = ["保持s1", "前往s1", "前往s2", "前往s3", "前往s4", "前往s5", "概率前往"]

# 状态转移函数 P(s'|s,a)
# 格式: "状态-动作-下一状态": 概率
P = {
    "s1-保持s1-s1": 1.0,
    "s1-前往s2-s2": 1.0,
    "s2-前往s1-s1": 1.0,
    "s2-前往s3-s3": 1.0,
    "s3-前往s4-s4": 1.0,
    "s3-前往s5-s5": 1.0,
    "s4-前往s5-s5": 1.0,
    "s4-概率前往-s2": 0.2,
    "s4-概率前往-s3": 0.4,
    "s4-概率前往-s4": 0.4,
}

# 奖励函数 R(s,a)
# 格式: "状态-动作": 奖励
R = {
    "s1-保持s1": -1,
    "s1-前往s2": 0,
    "s2-前往s1": -1,
    "s2-前往s3": -2,
    "s3-前往s4": -2,
    "s3-前往s5": 0,
    "s4-前往s5": 10,
    "s4-概率前往": 1,
}

gamma = 0.5

# MDP元组
MDP = (S, A, P, R, gamma)

# 策略1: 随机策略 (每个动作50%概率)
Pi_1 = {
    "s1-保持s1": 0.5,
    "s1-前往s2": 0.5,
    "s2-前往s1": 0.5,
    "s2-前往s3": 0.5,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.5,
    "s4-概率前往": 0.5,
}

# 策略2: 自定义策略
Pi_2 = {
    "s1-保持s1": 0.6,
    "s1-前往s2": 0.4,
    "s2-前往s1": 0.3,
    "s2-前往s3": 0.7,
    "s3-前往s4": 0.5,
    "s3-前往s5": 0.5,
    "s4-前往s5": 0.1,
    "s4-概率前往": 0.9,
}


def join(str1, str2):
    """把两个字符串通过"-"连接"""
    return str1 + '-' + str2


# -----------------------------------------------------------------------------
# MDP转化为MRP (边缘化)
# -----------------------------------------------------------------------------
print("\n" + "-" * 60)
print("MDP转化为MRP（边缘化）")
print("-" * 60)

# 转化后的MRP的状态转移矩阵
# 通过边缘化计算: P_mrp(s'|s) = Σ_a π(a|s) * P(s'|s,a)
P_from_mdp_to_mrp = [
    [0.5, 0.5, 0.0, 0.0, 0.0],  # s1: 50%留在s1, 50%去s2
    [0.5, 0.0, 0.5, 0.0, 0.0],  # s2: 50%去s1, 50%去s3
    [0.0, 0.0, 0.0, 0.5, 0.5],  # s3: 50%去s4, 50%去s5
    [0.0, 0.1, 0.2, 0.2, 0.5],  # s4: 边缘化后的结果
    [0.0, 0.0, 0.0, 0.0, 1.0],  # s5: 终止状态
]
P_from_mdp_to_mrp = np.array(P_from_mdp_to_mrp)

# 转化后的MRP的奖励函数
# 通过边缘化计算: R_mrp(s) = Σ_a π(a|s) * R(s,a)
R_from_mdp_to_mrp = [-0.5, -1.5, -1.0, 5.5, 0]

# 使用解析解计算MDP中的状态价值函数
V_mdp = compute(P_from_mdp_to_mrp, R_from_mdp_to_mrp, gamma, 5)
print("MDP中每个状态价值分别为（使用随机策略Pi_1）：")
print(V_mdp)


# =============================================================================
# 3.5 蒙特卡洛方法
# =============================================================================

print("\n" + "=" * 60)
print("3.5 蒙特卡洛方法")
print("=" * 60)


def sample(MDP, Pi, timestep_max, number):
    """
    采样函数
    MDP: 马尔可夫决策过程元组
    Pi: 策略
    timestep_max: 限制最长时间步
    number: 总共采样序列数
    返回: episodes列表，每个episode是(s, a, r, s_next)元组的列表
    """
    S, A, P, R, gamma = MDP
    episodes = []
    for _ in range(number):
        episode = []
        timestep = 0
        s = S[np.random.randint(4)]  # 随机选择初始状态(s1-s4)
        
        # 直到到达终止状态s5或超过最大步数
        while s != "s5" and timestep <= timestep_max:
            timestep += 1
            
            # 根据策略选择动作
            rand, temp = np.random.rand(), 0
            for a_opt in A:
                temp += Pi.get(join(s, a_opt), 0)
                if temp > rand:
                    a = a_opt
                    r = R.get(join(s, a), 0)
                    break
            
            # 根据状态转移概率确定下一状态
            rand, temp = np.random.rand(), 0
            for s_opt in S:
                temp += P.get(join(join(s, a), s_opt), 0)
                if temp > rand:
                    s_next = s_opt
                    break
            
            episode.append((s, a, r, s_next))
            s = s_next
        
        episodes.append(episode)
    return episodes


# 采样5条序列示例
episodes = sample(MDP, Pi_1, 20, 5)
print("\n采样序列示例：")
print('第一条序列:', episodes[0])
print('第二条序列:', episodes[1])
print('第五条序列:', episodes[4])


def MC(episodes, V, N, gamma):
    """
    蒙特卡洛方法估计状态价值
    episodes: 采样的序列列表
    V: 价值函数字典
    N: 状态访问次数字典
    gamma: 折扣因子
    """
    for episode in episodes:
        G = 0
        # 从后往前遍历（因为G_t = R_t + γ*G_{t+1}）
        for i in range(len(episode) - 1, -1, -1):
            (s, a, r, s_next) = episode[i]
            G = r + gamma * G
            N[s] = N[s] + 1
            # 增量更新: V(s) = V(s) + (1/N) * (G - V(s))
            V[s] = V[s] + (G - V[s]) / N[s]


# 使用蒙特卡洛方法估计状态价值
timestep_max = 20
episodes = sample(MDP, Pi_1, timestep_max, 1000)
gamma = 0.5
V = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
N = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
MC(episodes, V, N, gamma)

print("\n使用蒙特卡洛方法计算MDP的状态价值为：")
print(V)


# =============================================================================
# 3.6 占用度量
# =============================================================================

print("\n" + "=" * 60)
print("3.6 占用度量")
print("=" * 60)


def occupancy(episodes, s, a, timestep_max, gamma):
    """
    计算状态动作对(s,a)的占用度量
    episodes: 采样的序列列表
    s: 状态
    a: 动作
    timestep_max: 最大时间步
    gamma: 折扣因子
    返回: 占用度量值
    """
    rho = 0
    total_times = np.zeros(timestep_max)  # 记录每个时间步的访问次数
    occur_times = np.zeros(timestep_max)  # 记录(s,a)在每个时间步出现的次数
    
    for episode in episodes:
        for i in range(len(episode)):
            (s_opt, a_opt, r, s_next) = episode[i]
            total_times[i] += 1
            if s == s_opt and a == a_opt:
                occur_times[i] += 1
    
    for i in reversed(range(timestep_max)):
        if total_times[i]:
            rho += gamma**i * occur_times[i] / total_times[i]
    
    return (1 - gamma) * rho


# 采样序列用于计算占用度量
gamma = 0.5
timestep_max = 1000
episodes_1 = sample(MDP, Pi_1, timestep_max, 1000)
episodes_2 = sample(MDP, Pi_2, timestep_max, 1000)

# 计算两个策略的占用度量
rho_1 = occupancy(episodes_1, "s4", "概率前往", timestep_max, gamma)
rho_2 = occupancy(episodes_2, "s4", "概率前往", timestep_max, gamma)

print(f"策略1的占用度量 ρ(s4, 概率前往) = {rho_1}")
print(f"策略2的占用度量 ρ(s4, 概率前往) = {rho_2}")


# =============================================================================
# 结果对比
# =============================================================================

print("\n" + "=" * 60)
print("结果对比：解析解 vs 蒙特卡洛")
print("=" * 60)
print(f"{'状态':<6} {'解析解':<12} {'蒙特卡洛':<12}")
print("-" * 30)
states = ["s1", "s2", "s3", "s4", "s5"]
for i, s in enumerate(states):
    print(f"{s:<6} {V_mdp[i][0]:<12.4f} {V[s]:<12.4f}")

4 动态规划算法

4.1 简介

动态规划：将问题分解为子问题，保存子问题答案避免重复计算。

两种算法：

算法 核心方程
策略迭代 贝尔曼期望方程
价值迭代 贝尔曼最优方程

前提条件：需要知道完整的 MDP（状态转移函数、奖励函数），即"白盒环境"。

4.2 悬崖漫步环境

  • 4×12 网格，共48个状态
  • 起点：左下角 | 终点：右下角
  • 底部中间是悬崖
  • 每步奖励：-1 | 掉悬崖：-100

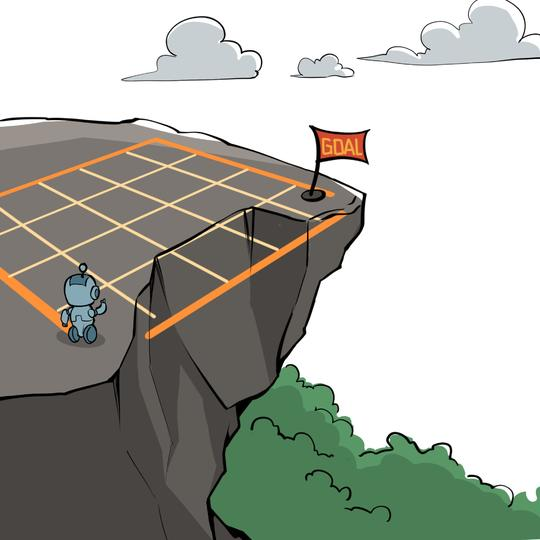
4.3 策略迭代算法

步骤 做什么
策略评估 按当前策略，算每个状态的得分
策略提升 在每个状态，贪心选得分最高的动作
再评估 用新策略重新算得分
再提升 看看还能不能更好

4.3.1 策略评估

目标：给定策略 π，计算状态价值函数 V

公式：

V ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ P ( s ′ ∣ s , a ) [ r + γ V ( s ′ ) ] V(s) = \sum_a \pi(a|s) \sum_{s'} P(s'|s,a) [r + \gamma V(s')] V(s)=a∑π(a∣s)s′∑P(s′∣s,a)[r+γV(s′)]

迭代更新 V，直到变化量 Δ < θ 收敛。

4.3.2 策略提升

目标：根据 V 改进策略 π

方法：贪心选择 Q 值最大的动作

π ( s ) = arg ⁡ max ⁡ a [ r ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ( s ′ ) ] \pi(s) = \arg\max_a \left[ r(s,a) + \gamma \sum_{s'} P(s'|s,a) V(s') \right] π(s)=argamax[r(s,a)+γs′∑P(s′∣s,a)V(s′)]

策略提升定理：新策略不比旧策略差

V π n e w ( s ) ≥ V π o l d ( s ) V^{\pi_{new}}(s) \geq V^{\pi_{old}}(s) Vπnew(s)≥Vπold(s)

4.3.3 策略迭代流程

π 0 → 评估 V π 0 → 提升 π 1 → 评估 V π 1 → 提升 π 2 → 评估 ⋯ → 提升 π ∗ \pi_0 \xrightarrow{评估} V^{\pi_0} \xrightarrow{提升} \pi_1 \xrightarrow{评估} V^{\pi_1} \xrightarrow{提升} \pi_2 \xrightarrow{评估} \cdots \xrightarrow{提升} \pi^* π0评估 Vπ0提升 π1评估 Vπ1提升 π2评估 ⋯提升 π∗

当 π 不再变化时，收敛到最优策略。

4.4 价值迭代算法

核心思想：不维护策略，直接用 max 更新 V

公式：

V ( s ) = max ⁡ a [ r ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ( s ′ ) ] V(s) = \max_a \left[ r(s,a) + \gamma \sum_{s'} P(s'|s,a) V(s') \right] V(s)=amax[r(s,a)+γs′∑P(s′∣s,a)V(s′)]

最后提取策略：

π ( s ) = arg ⁡ max ⁡ a [ r ( s , a ) + γ ∑ s ′ P ( s ′ ∣ s , a ) V ( s ′ ) ] \pi(s) = \arg\max_a \left[ r(s,a) + \gamma \sum_{s'} P(s'|s,a) V(s') \right] π(s)=argamax[r(s,a)+γs′∑P(s′∣s,a)V(s′)]

V 收敛后，用 argmax 提取最优策略。

本部分的代码

python 复制代码 
import copy


class CliffWalkingEnv:
    """ 悬崖漫步环境"""
    def __init__(self, ncol=12, nrow=4):
        self.ncol = ncol  # 定义网格世界的列
        self.nrow = nrow  # 定义网格世界的行
        # 转移矩阵P[state][action] = [(p, next_state, reward, done)]包含下一个状态和奖励
        self.P = self.createP()

    def createP(self):
        # 初始化
        P = [[[] for j in range(4)] for i in range(self.nrow * self.ncol)]
        # 4种动作, change[0]:上,change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)
        # 定义在左上角
        change = [[0, -1], [0, 1], [-1, 0], [1, 0]]
        for i in range(self.nrow):
            for j in range(self.ncol):
                for a in range(4):
                    # 位置在悬崖或者目标状态,因为无法继续交互,任何动作奖励都为0
                    if i == self.nrow - 1 and j > 0:
                        P[i * self.ncol + j][a] = [(1, i * self.ncol + j, 0,
                                                    True)]
                        continue
                    # 其他位置
                    next_x = min(self.ncol - 1, max(0, j + change[a][0]))
                    next_y = min(self.nrow - 1, max(0, i + change[a][1]))
                    next_state = next_y * self.ncol + next_x
                    reward = -1
                    done = False
                    # 下一个位置在悬崖或者终点
                    if next_y == self.nrow - 1 and next_x > 0:
                        done = True
                        if next_x != self.ncol - 1:  # 下一个位置在悬崖
                            reward = -100
                    P[i * self.ncol + j][a] = [(1, next_state, reward, done)]
        return P

class PolicyIteration:
    """ 策略迭代算法 """
    def __init__(self, env, theta, gamma):
        self.env = env
        self.v = [0] * self.env.ncol * self.env.nrow  # 初始化价值为0
        self.pi = [[0.25, 0.25, 0.25, 0.25]
                   for i in range(self.env.ncol * self.env.nrow)]  # 初始化为均匀随机策略
        self.theta = theta  # 策略评估收敛阈值
        self.gamma = gamma  # 折扣因子

    def policy_evaluation(self):  # 策略评估
        cnt = 1  # 计数器
        while 1:
            max_diff = 0
            new_v = [0] * self.env.ncol * self.env.nrow
            for s in range(self.env.ncol * self.env.nrow):
                qsa_list = []  # 开始计算状态s下的所有Q(s,a)价值
                for a in range(4):
                    qsa = 0
                    for res in self.env.P[s][a]:
                        p, next_state, r, done = res
                        qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
                        # 本章环境比较特殊,奖励和下一个状态有关,所以需要和状态转移概率相乘
                    qsa_list.append(self.pi[s][a] * qsa)
                new_v[s] = sum(qsa_list)  # 状态价值函数和动作价值函数之间的关系
                max_diff = max(max_diff, abs(new_v[s] - self.v[s]))
            self.v = new_v
            if max_diff < self.theta: break  # 满足收敛条件,退出评估迭代
            cnt += 1
        print("策略评估进行%d轮后完成" % cnt)

    def policy_improvement(self):  # 策略提升
        for s in range(self.env.nrow * self.env.ncol):
            qsa_list = []
            for a in range(4):
                qsa = 0
                for res in self.env.P[s][a]:
                    p, next_state, r, done = res
                    qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
                qsa_list.append(qsa)
            maxq = max(qsa_list)
            cntq = qsa_list.count(maxq)  # 计算有几个动作得到了最大的Q值
            # 让这些动作均分概率
            self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]
        print("策略提升完成")
        return self.pi

    def policy_iteration(self):  # 策略迭代
        while 1:
            self.policy_evaluation()
            old_pi = copy.deepcopy(self.pi)  # 将列表进行深拷贝,方便接下来进行比较
            new_pi = self.policy_improvement()
            if old_pi == new_pi: break

def print_agent(agent, action_meaning, disaster=[], end=[]):
    print("状态价值：")
    for i in range(agent.env.nrow):
        for j in range(agent.env.ncol):
            # 为了输出美观,保持输出6个字符
            print('%6.6s' % ('%.3f' % agent.v[i * agent.env.ncol + j]), end=' ')
        print()

    print("策略：")
    for i in range(agent.env.nrow):
        for j in range(agent.env.ncol):
            # 一些特殊的状态,例如悬崖漫步中的悬崖
            if (i * agent.env.ncol + j) in disaster:
                print('****', end=' ')
            elif (i * agent.env.ncol + j) in end:  # 目标状态
                print('EEEE', end=' ')
            else:
                a = agent.pi[i * agent.env.ncol + j]
                pi_str = ''
                for k in range(len(action_meaning)):
                    pi_str += action_meaning[k] if a[k] > 0 else 'o'
                print(pi_str, end=' ')
        print()

class ValueIteration:
    """ 价值迭代算法 """
    def __init__(self, env, theta, gamma):
        self.env = env
        self.v = [0] * self.env.ncol * self.env.nrow  # 初始化价值为0
        self.theta = theta  # 价值收敛阈值
        self.gamma = gamma
        # 价值迭代结束后得到的策略
        self.pi = [None for i in range(self.env.ncol * self.env.nrow)]

    def value_iteration(self):
        cnt = 0
        while 1:
            max_diff = 0
            new_v = [0] * self.env.ncol * self.env.nrow
            for s in range(self.env.ncol * self.env.nrow):
                qsa_list = []  # 开始计算状态s下的所有Q(s,a)价值
                for a in range(4):
                    qsa = 0
                    for res in self.env.P[s][a]:
                        p, next_state, r, done = res
                        qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
                    qsa_list.append(qsa)  # 这一行和下一行代码是价值迭代和策略迭代的主要区别
                new_v[s] = max(qsa_list)
                max_diff = max(max_diff, abs(new_v[s] - self.v[s]))
            self.v = new_v
            if max_diff < self.theta: break  # 满足收敛条件,退出评估迭代
            cnt += 1
        print("价值迭代一共进行%d轮" % cnt)
        self.get_policy()

    def get_policy(self):  # 根据价值函数导出一个贪婪策略
        for s in range(self.env.nrow * self.env.ncol):
            qsa_list = []
            for a in range(4):
                qsa = 0
                for res in self.env.P[s][a]:
                    p, next_state, r, done = res
                    qsa += p * (r + self.gamma * self.v[next_state] * (1 - done))
                qsa_list.append(qsa)
            maxq = max(qsa_list)
            cntq = qsa_list.count(maxq)  # 计算有几个动作得到了最大的Q值
            # 让这些动作均分概率
            self.pi[s] = [1 / cntq if q == maxq else 0 for q in qsa_list]


env = CliffWalkingEnv()
action_meaning = ['^', 'v', '<', '>']
theta = 0.001
gamma = 0.9

# 价值迭代
agent = ValueIteration(env, theta, gamma)
agent.value_iteration()
print_agent(agent, action_meaning, list(range(37, 47)), [47])

# 策略迭代
agent = PolicyIteration(env, theta, gamma)
agent.policy_iteration()
print_agent(agent, action_meaning, list(range(37, 47)), [47])

5 时序差分算法

5.1 时序差分 vs 蒙特卡洛

核心区别

方法 用什么来更新
蒙特卡洛 等整个序列结束，用真实的完整回报 G t G_t Gt
时序差分 只走一步，用一步奖励 + 下一状态的估计值

公式对比

蒙特卡洛：

V ( S t ) ← V ( S t ) + α [ G t − V ( S t ) ] V(S_t) \leftarrow V(S_t) + \alpha \left[G_t - V(S_t)\right] V(St)←V(St)+α[Gt−V(St)]

其中 G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots Gt=Rt+1+γRt+2+γ2Rt+3+⋯（要等到序列结束才能算出来）

时序差分：

V ( S t ) ← V ( S t ) + α [ R t + 1 + γ V ( S t + 1 ) − V ( S t ) ] V(S_t) \leftarrow V(S_t) + \alpha \left[R_{t+1} + \gamma V(S_{t+1}) - V(S_t)\right] V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]

关键思想 ：把后面一长串 γ 2 R t + 3 + γ 3 R t + 4 + ⋯ \gamma^2 R_{t+3} + \gamma^3 R_{t+4} + \cdots γ2Rt+3+γ3Rt+4+⋯ 全都压缩 成一个 V ( S t + 1 ) V(S_{t+1}) V(St+1)。

优缺点对比

蒙特卡洛 时序差分
需要等序列结束 ✅ 是 ❌ 不需要
偏差 无（用真实回报） 有（用估计值）
方差 高（整条路径随机性累积） 低（只有一步随机性）

5.2 Sarsa 算法

核心公式

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)\right] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)−Q(St,At)]

符号说明

符号 含义
S t S_t St 当前状态
A t A_t At 当前执行的动作
R t + 1 R_{t+1} Rt+1 执行动作后得到的奖励
S t + 1 S_{t+1} St+1 到达的新状态
A t + 1 A_{t+1} At+1 在新状态下实际选择的下一个动作
α \alpha α 学习率
γ \gamma γ 折扣因子

公式结构

Q ( S t , A t ) ⏟ 旧估计 ← Q ( S t , A t ) ⏟ 旧估计 + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) ⏟ TD目标 − Q ( S t , A t ) ⏟ 旧估计 ] \underbrace{Q(S_t, A_t)}{\text{旧估计}} \leftarrow \underbrace{Q(S_t, A_t)}{\text{旧估计}} + \alpha \left[\underbrace{R_{t+1} + \gamma Q(S_{t+1}, A_{t+1})}{\text{TD目标}} - \underbrace{Q(S_t, A_t)}{\text{旧估计}}\right] 旧估计 Q(St,At)←旧估计 Q(St,At)+α TD目标 Rt+1+γQ(St+1,At+1)−旧估计 Q(St,At)

也可以写成：

Q ( S t , A t ) ← Q ( S t , A t ) + α ⋅ δ t ⏟ TD误差 Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \cdot \underbrace{\delta_t}_{\text{TD误差}} Q(St,At)←Q(St,At)+α⋅TD误差 δt

和策略迭代的关系

复制代码 
策略迭代 = 策略评估 + 策略改进
           ↓           ↓
        算出V或Q    根据Q选更好的动作

策略评估：给定策略 π \pi π，计算它的价值函数 V π V^\pi Vπ 或 Q π Q^\pi Qπ

策略改进：根据价值函数，用贪婪方法得到更好的策略

动态规划的局限

动态规划做策略评估时，需要用这个公式：

V ( s ) = ∑ a π ( a ∣ s ) ∑ s ′ P ( s ′ ∣ s , a ) [ R + γ V ( s ′ ) ] V(s) = \sum_{a}\pi(a|s)\sum_{s'}P(s'|s,a)\left[R + \gamma V(s')\right] V(s)=a∑π(a∣s)s′∑P(s′∣s,a)[R+γV(s′)]

必须知道 P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a)，也就是环境的状态转移概率。但在实际问题中，我们往往不知道环境模型！

Sarsa 的角色：无模型的策略评估

Sarsa 用采样代替了对环境模型的依赖：

动态规划 Sarsa
策略评估 用 P ( s ′ ∣ s , a ) P(s'|s,a) P(s′∣s,a) 计算期望 用实际交互采样来估计
需要环境模型 ✅ 需要 ❌ 不需要
评估对象 V ( s ) V(s) V(s) 或 Q ( s , a ) Q(s,a) Q(s,a) Q ( s , a ) Q(s,a) Q(s,a)

策略改进方式的区别

动态规划用纯贪婪：

π ( s ) = arg ⁡ max ⁡ a Q ( s , a ) \pi(s) = \arg\max_a Q(s,a) π(s)=argamaxQ(s,a)

Sarsa 用 ε-贪婪：

π ( s ) = { arg ⁡ max ⁡ a Q ( s , a ) 概率 1 − ε 随机动作 概率 ε \pi(s) = \begin{cases} \arg\max_a Q(s,a) & \text{概率 } 1-\varepsilon \\ \text{随机动作} & \text{概率 } \varepsilon \end{cases} π(s)={argmaxaQ(s,a)随机动作概率 1−ε概率 ε

为什么要加随机？因为不知道环境模型，必须通过探索来发现哪些动作更好。

评估完整度的区别

动态规划的策略迭代：策略评估要做到完全收敛，然后再改进策略。

Sarsa：不等评估完全收敛，走一步就更新一次 Q，同时也在改进策略 。这其实是广义策略迭代的思想：评估和改进交替进行，不用等一个完全结束再做另一个。

算法分类图

复制代码 
        需要环境模型吗？
              │
       ┌──────┴──────┐
       │             │
      需要          不需要
       │             │
    动态规划      无模型方法
       │             │
   ┌───┴───┐    ┌────┴────┐
   │       │    │         │
 策略迭代 价值迭代 蒙特卡洛   时序差分
                          │
                     ┌────┴────┐
                     │         │
                   Sarsa    Q-learning

5.3 多步 Sarsa 算法

动机：单步 Sarsa vs 蒙特卡洛

方法 用什么估计回报
蒙特卡洛 完整序列的真实回报 G t = R t + 1 + γ R t + 2 + γ 2 R t + 3 + ⋯ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \cdots Gt=Rt+1+γRt+2+γ2Rt+3+⋯
单步 Sarsa 一步奖励 + 估计值 R t + 1 + γ Q ( S t + 1 , A t + 1 ) R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) Rt+1+γQ(St+1,At+1)

一个用全部真实奖励，一个只用一步。能不能折中一下？ 用 n 步真实奖励 + 后面的估计值？

核心思想

n 步 Sarsa：往前看 n 步真实奖励，然后用第 n+1 步的 Q 估计值代替剩余部分。

公式对比

单步 Sarsa（n=1）：

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha\left[R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)\right] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)−Q(St,At)]

2 步 Sarsa（n=2）：

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ R t + 2 + γ 2 Q ( S t + 2 , A t + 2 ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha\left[R_{t+1} + \gamma R_{t+2} + \gamma^2 Q(S_{t+2}, A_{t+2}) - Q(S_t, A_t)\right] Q(St,At)←Q(St,At)+α[Rt+1+γRt+2+γ2Q(St+2,At+2)−Q(St,At)]

n 步 Sarsa（通用公式）：

Q ( S t , A t ) ← Q ( S t , A t ) + α [ ∑ k = 0 n − 1 γ k R t + k + 1 + γ n Q ( S t + n , A t + n ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha\left[\sum_{k=0}^{n-1}\gamma^k R_{t+k+1} + \gamma^n Q(S_{t+n}, A_{t+n}) - Q(S_t, A_t)\right] Q(St,At)←Q(St,At)+α[k=0∑n−1γkRt+k+1+γnQ(St+n,At+n)−Q(St,At)]

为什么要多步？

单步 Sarsa 多步 Sarsa 蒙特卡洛
偏差 大（估计值不准） 中等 无
方差 小 中等 大
需要等待 1步 n步 整个序列

多步 Sarsa 是一个折中 ：比单步 Sarsa 偏差更小 （用了更多真实奖励），比蒙特卡洛 方差更小（不用等到最后）。

直观理解

复制代码 
蒙特卡洛 ←--------------- 多步Sarsa ---------------→ 单步Sarsa
   ↑               ↑                ↑
  n=∞            n=5,10...          n=1
  
全用真实奖励    部分真实+部分估计    几乎全靠估计
无偏但高方差    折中                有偏但低方差

实际效果

在悬崖漫步实验中，5步 Sarsa 比单步 Sarsa 收敛更快，因为它能更快地把后面的信息传递到前面的状态。

5.4 Q-learning 算法

核心公式

Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ max ⁡ a ′ Q ( S t + 1 , a ′ ) − Q ( S t , A t ) ] Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha\left[R_{t+1} + \gamma \max_{a'} Q(S_{t+1}, a') - Q(S_t, A_t)\right] Q(St,At)←Q(St,At)+α[Rt+1+γa′maxQ(St+1,a′)−Q(St,At)]

和 Sarsa 的唯一区别

Sarsa Q-learning
下一步用什么 Q ( S t + 1 , A t + 1 ) Q(S_{t+1}, A_{t+1}) Q(St+1,At+1) max ⁡ a ′ Q ( S t + 1 , a ′ ) \max_{a'} Q(S_{t+1}, a') maxa′Q(St+1,a′)
含义 实际会选的动作 最优的动作

在线策略 vs 离线策略

Sarsa Q-learning
需要的数据 ( S , A , R , S ′ , A ′ ) (S, A, R, S', A') (S,A,R,S′,A′) ( S , A , R , S ′ ) (S, A, R, S') (S,A,R,S′)
能用旧数据吗 ❌ 不能 ✅ 能
能用别人的数据吗 ❌ 不能 ✅ 能
策略类型 在线策略 离线策略

离线策略的优势：数据可以反复利用，样本效率高，这是后面 DQN 经验回放的基础。

学到的策略差异

Sarsa Q-learning
风格 保守、安全 激进、最优
悬崖漫步的路线 远离悬崖 贴着悬崖走
原因 考虑了探索时可能犯错 假设之后都选最优

算法流程

复制代码 
初始化 Q(s,a) = 0

重复很多个序列：
    初始化状态 S
    
    循环直到序列结束：
        用 ε-贪婪根据 Q 选动作 A
        执行 A，得到 R 和 S'
        
        更新：Q(S,A) ← Q(S,A) + α[R + γ·max Q(S',a') - Q(S,A)]
        
        S ← S'

注意：和 Sarsa 不同，不需要先选出 A ′ A' A′。

为什么叫 Q-learning？

因为它直接学习的是最优动作价值函数 Q ∗ ( s , a ) Q^*(s,a) Q∗(s,a)，而不是某个特定策略的 Q 值。

贝尔曼最优方程：

Q ∗ ( s , a ) = E [ R + γ max ⁡ a ′ Q ∗ ( S ′ , a ′ ) ] Q^*(s,a) = \mathbb{E}\left[R + \gamma \max_{a'} Q^*(S', a')\right] Q∗(s,a)=E[R+γa′maxQ∗(S′,a′)]

Q-learning 就是在用采样的方式逼近这个方程。

一句话总结

Q-learning = 用 TD 方法 + 取 max + 离线策略，直接学最优 Q 值

5.5 本章总结

算法公式汇总

算法 更新公式
TD（更新V） V ( S t ) ← V ( S t ) + α [ R t + 1 + γ V ( S t + 1 ) − V ( S t ) ] V(S_t) \leftarrow V(S_t) + \alpha[R_{t+1} + \gamma V(S_{t+1}) - V(S_t)] V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]
Sarsa Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ Q ( S t + 1 , A t + 1 ) − Q ( S t , A t ) ] Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma Q(S_{t+1},A_{t+1}) - Q(S_t,A_t)] Q(St,At)←Q(St,At)+α[Rt+1+γQ(St+1,At+1)−Q(St,At)]
Q-learning Q ( S t , A t ) ← Q ( S t , A t ) + α [ R t + 1 + γ max ⁡ a ′ Q ( S t + 1 , a ′ ) − Q ( S t , A t ) ] Q(S_t,A_t) \leftarrow Q(S_t,A_t) + \alpha[R_{t+1} + \gamma \max_{a'} Q(S_{t+1},a') - Q(S_t,A_t)] Q(St,At)←Q(St,At)+α[Rt+1+γmaxa′Q(St+1,a′)−Q(St,At)]

Sarsa vs Q-learning 核心对比

Sarsa Q-learning
下一步动作 实际选的 A t + 1 A_{t+1} At+1 最优的 max ⁡ \max max
策略类型 在线策略 离线策略
能用旧数据 ❌ ✅
学到的策略 保守 最优

本部分的所有代码

python 复制代码 
"""
第5章 时序差分算法
包含：Sarsa、n步Sarsa、Q-learning
环境：悬崖漫步（Cliff Walking）
"""

import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm


# ==================== 环境 ====================

class CliffWalkingEnv:
    """悬崖漫步环境"""
    
    def __init__(self, ncol, nrow):
        self.nrow = nrow
        self.ncol = ncol
        self.x = 0
        self.y = self.nrow - 1
    
    def step(self, action):
        """
        执行动作，返回下一状态、奖励、是否结束
        动作：0上 1下 2左 3右
        """
        change = [[0, -1], [0, 1], [-1, 0], [1, 0]]
        self.x = min(self.ncol - 1, max(0, self.x + change[action][0]))
        self.y = min(self.nrow - 1, max(0, self.y + change[action][1]))
        next_state = self.y * self.ncol + self.x
        reward = -1
        done = False
        
        if self.y == self.nrow - 1 and self.x > 0:
            done = True
            if self.x != self.ncol - 1:  # 掉进悬崖
                reward = -100
        return next_state, reward, done
    
    def reset(self):
        """重置环境"""
        self.x = 0
        self.y = self.nrow - 1
        return self.y * self.ncol + self.x


# ==================== Sarsa算法 ====================

class Sarsa:
    """Sarsa算法"""
    
    def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])
        self.n_action = n_action
        self.alpha = alpha      # 学习率
        self.gamma = gamma      # 折扣因子
        self.epsilon = epsilon  # ε-贪婪参数
    
    def take_action(self, state):
        """ε-贪婪选动作"""
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action
    
    def best_action(self, state):
        """返回最优动作（用于打印策略）"""
        Q_max = np.max(self.Q_table[state])
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a
    
    def update(self, s0, a0, r, s1, a1):
        """Sarsa更新：用实际选的动作a1"""
        td_error = r + self.gamma * self.Q_table[s1, a1] - self.Q_table[s0, a0]
        self.Q_table[s0, a0] += self.alpha * td_error


# ==================== n步Sarsa算法 ====================

class NStepSarsa:
    """n步Sarsa算法"""
    
    def __init__(self, n, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])
        self.n_action = n_action
        self.alpha = alpha
        self.gamma = gamma
        self.epsilon = epsilon
        self.n = n  # n步
        self.state_list = []   # 存储轨迹中的状态
        self.action_list = []  # 存储轨迹中的动作
        self.reward_list = []  # 存储轨迹中的奖励
    
    def take_action(self, state):
        """ε-贪婪选动作"""
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action
    
    def best_action(self, state):
        """返回最优动作"""
        Q_max = np.max(self.Q_table[state])
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a
    
    def update(self, s0, a0, r, s1, a1, done):
        """n步Sarsa更新"""
        self.state_list.append(s0)
        self.action_list.append(a0)
        self.reward_list.append(r)
        
        if len(self.state_list) == self.n:
            G = self.Q_table[s1, a1]
            for i in reversed(range(self.n)):
                G = self.gamma * G + self.reward_list[i]
                if done and i > 0:
                    s = self.state_list[i]
                    a = self.action_list[i]
                    self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])
            
            s = self.state_list.pop(0)
            a = self.action_list.pop(0)
            self.reward_list.pop(0)
            self.Q_table[s, a] += self.alpha * (G - self.Q_table[s, a])
        
        if done:
            self.state_list = []
            self.action_list = []
            self.reward_list = []


# ==================== Q-learning算法 ====================

class QLearning:
    """Q-learning算法"""
    
    def __init__(self, ncol, nrow, epsilon, alpha, gamma, n_action=4):
        self.Q_table = np.zeros([nrow * ncol, n_action])
        self.n_action = n_action
        self.alpha = alpha
        self.gamma = gamma
        self.epsilon = epsilon
    
    def take_action(self, state):
        """ε-贪婪选动作"""
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.n_action)
        else:
            action = np.argmax(self.Q_table[state])
        return action
    
    def best_action(self, state):
        """返回最优动作"""
        Q_max = np.max(self.Q_table[state])
        a = [0 for _ in range(self.n_action)]
        for i in range(self.n_action):
            if self.Q_table[state, i] == Q_max:
                a[i] = 1
        return a
    
    def update(self, s0, a0, r, s1):
        """Q-learning更新：用max，不需要a1"""
        td_error = r + self.gamma * self.Q_table[s1].max() - self.Q_table[s0, a0]
        self.Q_table[s0, a0] += self.alpha * td_error


# ==================== 工具函数 ====================

def print_agent(agent, env, action_meaning, disaster=[], end=[]):
    """打印策略"""
    for i in range(env.nrow):
        for j in range(env.ncol):
            if (i * env.ncol + j) in disaster:
                print('****', end=' ')
            elif (i * env.ncol + j) in end:
                print('EEEE', end=' ')
            else:
                a = agent.best_action(i * env.ncol + j)
                pi_str = ''
                for k in range(len(action_meaning)):
                    pi_str += action_meaning[k] if a[k] > 0 else 'o'
                print(pi_str, end=' ')
        print()


def train_sarsa(env, agent, num_episodes):
    """训练Sarsa"""
    return_list = []
    for _ in tqdm(range(num_episodes), desc='Sarsa'):
        episode_return = 0
        state = env.reset()
        action = agent.take_action(state)
        done = False
        
        while not done:
            next_state, reward, done = env.step(action)
            next_action = agent.take_action(next_state)
            episode_return += reward
            agent.update(state, action, reward, next_state, next_action)
            state = next_state
            action = next_action
        
        return_list.append(episode_return)
    return return_list


def train_nstep_sarsa(env, agent, num_episodes):
    """训练n步Sarsa"""
    return_list = []
    for _ in tqdm(range(num_episodes), desc=f'{agent.n}-step Sarsa'):
        episode_return = 0
        state = env.reset()
        action = agent.take_action(state)
        done = False
        
        while not done:
            next_state, reward, done = env.step(action)
            next_action = agent.take_action(next_state)
            episode_return += reward
            agent.update(state, action, reward, next_state, next_action, done)
            state = next_state
            action = next_action
        
        return_list.append(episode_return)
    return return_list


def train_qlearning(env, agent, num_episodes):
    """训练Q-learning"""
    return_list = []
    for _ in tqdm(range(num_episodes), desc='Q-learning'):
        episode_return = 0
        state = env.reset()
        done = False
        
        while not done:
            action = agent.take_action(state)
            next_state, reward, done = env.step(action)
            episode_return += reward
            agent.update(state, action, reward, next_state)
            state = next_state
        
        return_list.append(episode_return)
    return return_list


def plot_returns(return_list, title):
    """绘制回报曲线"""
    plt.figure(figsize=(10, 6))
    plt.plot(return_list)
    plt.xlabel('Episodes')
    plt.ylabel('Returns')
    plt.title(title)
    plt.show()


# ==================== 主函数 ====================

def main():
    # 环境参数
    ncol, nrow = 12, 4
    
    # 算法参数
    epsilon = 0.1
    alpha = 0.1
    gamma = 0.9
    num_episodes = 500
    
    np.random.seed(0)
    action_meaning = ['^', 'v', '<', '>']
    cliff = list(range(37, 47))  # 悬崖位置
    end = [47]  # 终点位置
    
    # ========== 1. Sarsa ==========
    print("\n" + "="*50)
    print("训练 Sarsa")
    print("="*50)
    
    env = CliffWalkingEnv(ncol, nrow)
    agent_sarsa = Sarsa(ncol, nrow, epsilon, alpha, gamma)
    return_list_sarsa = train_sarsa(env, agent_sarsa, num_episodes)
    
    print("\nSarsa 最终策略：")
    print_agent(agent_sarsa, env, action_meaning, cliff, end)
    plot_returns(return_list_sarsa, 'Sarsa on Cliff Walking')
    
    # ========== 2. 5步Sarsa ==========
    print("\n" + "="*50)
    print("训练 5步Sarsa")
    print("="*50)
    
    np.random.seed(0)
    env = CliffWalkingEnv(ncol, nrow)
    agent_nstep = NStepSarsa(n=5, ncol=ncol, nrow=nrow, 
                             epsilon=epsilon, alpha=alpha, gamma=gamma)
    return_list_nstep = train_nstep_sarsa(env, agent_nstep, num_episodes)
    
    print("\n5步Sarsa 最终策略：")
    print_agent(agent_nstep, env, action_meaning, cliff, end)
    plot_returns(return_list_nstep, '5-step Sarsa on Cliff Walking')
    
    # ========== 3. Q-learning ==========
    print("\n" + "="*50)
    print("训练 Q-learning")
    print("="*50)
    
    np.random.seed(0)
    env = CliffWalkingEnv(ncol, nrow)
    agent_ql = QLearning(ncol, nrow, epsilon, alpha, gamma)
    return_list_ql = train_qlearning(env, agent_ql, num_episodes)
    
    print("\nQ-learning 最终策略：")
    print_agent(agent_ql, env, action_meaning, cliff, end)
    plot_returns(return_list_ql, 'Q-learning on Cliff Walking')
    
    # ========== 4. 对比三种算法 ==========
    print("\n" + "="*50)
    print("三种算法对比")
    print("="*50)
    
    plt.figure(figsize=(12, 6))
    plt.plot(return_list_sarsa, label='Sarsa', alpha=0.7)
    plt.plot(return_list_nstep, label='5-step Sarsa', alpha=0.7)
    plt.plot(return_list_ql, label='Q-learning', alpha=0.7)
    plt.xlabel('Episodes')
    plt.ylabel('Returns')
    plt.title('Comparison of TD Algorithms')
    plt.legend()
    plt.show()


if __name__ == '__main__':
    main()

6 Dyan-Q算法

6.1 核心概念

Dyna-Q 是一种基于模型的强化学习算法，核心思想是：

真实学习 + 想象复习 = 学得更快

类型 说明
Q-learning 用真实经历更新 Q 表
Q-planning 用过去的记忆反复复习
Model 记忆库，存储过去的经历

6.2 算法流程

复制代码 
每走一步：
1. 执行 1 次 Q-learning（真实学习）
2. 把经历存入 model（记到错题本）
3. 执行 n 次 Q-planning（翻错题本复习 n 遍）

Q_table大概长这样：

复制代码 
           动作0    动作1    动作2    动作3
          (上)     (下)     (左)     (右)
状态0    [-1.2,   -0.5,   -2.0,    0.8  ]
状态1    [-0.3,   -1.0,    0.2,    1.5  ]
状态2    [ 0.5,   -0.8,   -0.1,    2.0  ]
...
状态47   [ 0.0,    0.0,    0.0,    0.0  ]

本部分的所有代码

python 复制代码 
import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm
import random
import time

class CliffWalkingEnv:
    def __init__(self, ncol, nrow):
        self.nrow = nrow
        self.ncol = ncol
        self.x = 0
        self.y = self.nrow - 1
    
    def step(self,action):
        change=[[0,-1],[0,1],[-1,0],[1,0]]  # ← 去掉多余的括号
        self.x=min(self.ncol-1,max(0,self.x+change[action][0]))
        self.y=min(self.nrow-1,max(0,self.y+change[action][1]))
        next_state=self.y*self.ncol+self.x
        reward=-1
        done=False
        if self.y==self.nrow-1 and self.x>0:
            done=True
            if self.x!=self.ncol-1:
                reward=-100
        return next_state,reward,done
    
    def reset(self): # 这里其实是左下角
        self.x=0
        self.y=self.nrow-1
        return self.y*self.ncol+self.x

class DynaQ:
    def __init__(self,ncol,nrow,epsilon,alpha,gamma,planning_steps,n_action=4):
        self.Q_table=np.zeros([nrow*ncol,n_action])
        self.model=dict()
        self.n_action=n_action
        self.alpha=alpha
        self.gamma=gamma
        self.epsilon=epsilon
        self.planning_steps=planning_steps

    def take_action(self,state):
        if np.random.random()<self.epsilon:
            action=np.random.randint(self.n_action)
        else:
            action=np.argmax(self.Q_table[state])
        return action
    
    def q_learning(self,s0,a0,r,s1):
        td_error=r+self.gamma*self.Q_table[s1].max()-self.Q_table[s0,a0]
        self.Q_table[s0,a0]+=self.alpha*td_error
    
    def update(self,s0,a0,r,s1):
        self.q_learning(s0,a0,r,s1)
        self.model[(s0,a0)]=(r,s1)
        for _ in range(self.planning_steps):
            s,a=random.choice(list(self.model.keys()))
            r_,s_=self.model[(s,a)]
            self.q_learning(s,a,r_,s_)
    
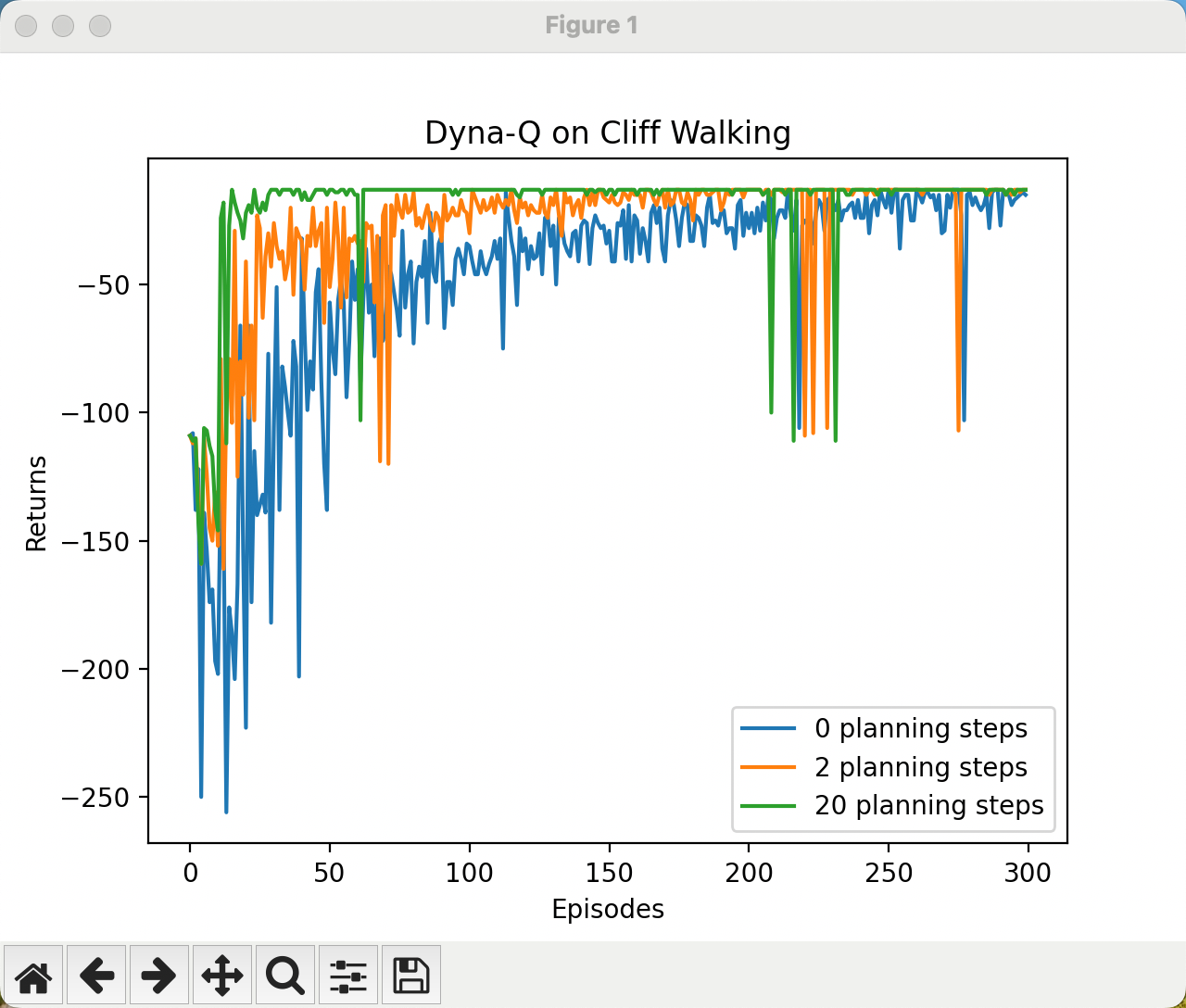
def DynaQ_CliffWalking(n_planning):
    ncol=12
    nrow=4
    env=CliffWalkingEnv(ncol,nrow)
    agent=DynaQ(ncol,nrow,epsilon=0.01,alpha=0.1,gamma=0.9,planning_steps=n_planning)
    num_episodes=300
    
    return_list=[]
    for i in range(10):
        with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes / 10)):
                episode_return=0
                state=env.reset()
                done=False
                while not done:
                    action=agent.take_action(state)
                    next_state,reward,done=env.step(action)
                    agent.update(state,action,reward,next_state)
                    state=next_state
                    episode_return+=reward
                return_list.append(episode_return)
                if (i_episode+1)%10==0:
                    pbar.set_postfix({
                        'episode':
                        '%d' % (i_episode + 1 + i * (num_episodes // 10)),
                        'return':
                        '%.3f' % np.mean(return_list[-10:])
                    })
                pbar.update(1) # 更新进度条
    return return_list
    
np.random.seed(0)
random.seed(0)
n_planning_list = [0, 2, 20]
for n_planning in n_planning_list:
    print('Q-planning步数为：%d' % n_planning)
    time.sleep(0.5)
    return_list = DynaQ_CliffWalking(n_planning)
    episodes_list = list(range(len(return_list)))
    plt.plot(episodes_list,
             return_list,
             label=str(n_planning) + ' planning steps')
plt.legend()
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Dyna-Q on {}'.format('Cliff Walking'))
plt.show()
相关推荐
独自破碎E2 小时前
解释一下向量数据库中的HNSW、LSH和PQ
gpt·语言模型
十六年开源服务商3 小时前
WordPress集成GoogleAnalytics最佳实践指南
前端·人工智能·机器学习
咚咚王者4 小时前
人工智能之核心基础 机器学习 第十四章 半监督与自监督学习总结归纳
人工智能·学习·机器学习
Sherry Wangs5 小时前
【ML】机器学习基础
人工智能·机器学习
专注VB编程开发20年5 小时前
MQTT傻瓜化调用组件，零成本学习.NET开发，上位机开发
学习·机器学习·.net
computersciencer5 小时前
用最小二乘法求解多元一次方程模型的参数
人工智能·机器学习·最小二乘法
武子康5 小时前
大数据-214 K-Means 聚类实战：自写算法验证 + sklearn KMeans 参数/labels_/fit_predict 速通
大数据·后端·机器学习
LDG_AGI5 小时前
【机器学习】深度学习推荐系统（二十六）：X 推荐算法多模型融合机制详解
人工智能·分布式·深度学习·算法·机器学习·推荐算法
Sherry Wangs5 小时前
【ML】语言模型 & GPUs
人工智能·语言模型·自然语言处理
热门推荐
01GitHub 镜像站点02Linux下V2Ray安装配置指南03Labelme从安装到标注：零基础完整指南04AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南05Claude Code Skills 实用使用手册06UV安装并设置国内源07网站改了域名，如何查找？082025年大语言模型技术全景报告09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10百度网盘偷偷给电脑“降频”？