手把手实现蚁群算法：从数学原理到代码实践

Narrastory2026-01-16 15:10

2026.01 | ming

蚁群算法，这可是大熟人了，在很多领域你都能看到它的身影，它算是优化算法中的经典了。如果你还不了解蚁群算法的基本原理及其应用场景，不必担心------本文将带你从零开始，逐步理解蚁群算法的思想，并手把手实现它。

蚁群算法本身，非常擅长求解离散路径规划问题，如最短路径、物流配送优化、网络路由选择等；但是如果你掌握了蚁群算法的设计思想，你完全可以将其推广至各类组合优化与决策问题中（如任务调度、资源分配、动态系统优化等）。因此，本文不仅关注算法实现，更注重其背后的设计思想。

注意：本文使用Python语言进行蚁群算法的实现与讲解，但是如果你不会Python也没关系，Python代码简单易懂，如果你掌握其它计算机语言，那么Python代码阅读起来会非常轻松。

一. 简介

蚁群算法的核心灵感来源于自然界中蚂蚁群体通过信息素（pheromone）协作寻找最短路径的行为。在自然界中，蚂蚁在外出寻找食物时，会在路径上释放一种称为"信息素"的化学物质。其他蚂蚁能够感知到这种物质，并更倾向于选择信息素浓度较高的路径。随着越来越多的蚂蚁走过同一条路径，该路径上的信息素会逐渐累积，从而吸引更多蚂蚁，形成一种正反馈机制。同时，信息素也会随着时间挥发，使得那些较少被选择的路径逐渐被"遗忘"。这种基于集体行为的自组织过程，使得蚂蚁群体能够在没有中央调度的情况下，高效地找到从巢穴到食物源的最短路径。

如果你还不理解，没关系，我们就从"蚂蚁搬糖"这个例子来形象的解释蚂蚁从发现糖到召集小伙伴来搬糖这个完整的过程是如何发生的：

想象一下，你是一只在草地上找糖吃的蚂蚁。

第一步：刚开始，啥也不知道

你和几百只蚂蚁兄弟从窝里出发，去找一块不远处的糖。一开始，大家都没有目标，所以就会到处瞎走，路线弯弯曲曲，各不相同。

第二步：谁先找到，谁就留下"香味导航"

有一只运气好的蚂蚁，歪打正着，找到糖了。它非常兴奋，会立刻沿着自己来的路往回走。关键来了：它一边走，一边会在地上释放一种特殊的"信息素"（你可以理解为一种香味、一条看不见的足迹线）。

这条"香味线"就是在告诉其他蚂蚁："兄弟们！我这条路通到食物！快过来！"

第三步：其他蚂蚁闻香而动

其他还在乱转的蚂蚁，突然闻到了这股香味。它们会怎么想？ "咦？有味道！肯定有兄弟找到好吃的了！" 于是，它们会大概率选择朝着香味更浓的方向走（当然，也会有概率朝其它方向走，这就是探索的部分）。香味越浓，说明走这条路的蚂蚁越多，这条路很可能就更短、更好走。

第四步：最短的路，香味变得最快最浓

现在，假设从蚂蚁窝到糖有两条路：一条直路（短） ，一条弯路（长）。

  • 走短路的蚂蚁，来回一趟时间快，在单位时间内能在这条路上往返更多次，留下更多次的香味。并且香味还没挥发完就又立马得到新的补充。
  • 走长路的蚂蚁，来回一趟耗时久，香味挥发的就多，并且香味补充得慢。

这样，短路上的香味浓度，就会以更快的速度增长，变得越来越浓。而长路上的香味，因为蚂蚁走得慢，加上风吹日晒（信息素会自然挥发），相对就淡一些。

第五步：滚雪球效应------大家都走最优路

新出发的蚂蚁们，面对一条"香味超浓的短路径"和一条"香味淡淡的长路径"，几乎都会选择短的。选择短路的蚂蚁越多，留下的香味就又越多，这条路就变得更有吸引力。

最终，几乎所有的蚂蚁都会集中到最短、最优的那条路径上，排成一条整齐的运输大队。而那条又长又弯的路，就被大家遗忘了。

二. 数学原理与流程

接下来，我们就以经典的旅行商问题为背景，来详细讲解蚁群算法。旅行商问题可以这样描述：在平面上随机散布着若干个城市（点），现从任意一个城市出发，要求不重复地经过所有城市，最后返回起点。我们的目标是找到一条长度最短的行走路径。换句话说，就是要用一条最短的连线，将所有城市连接成一个闭合环路。

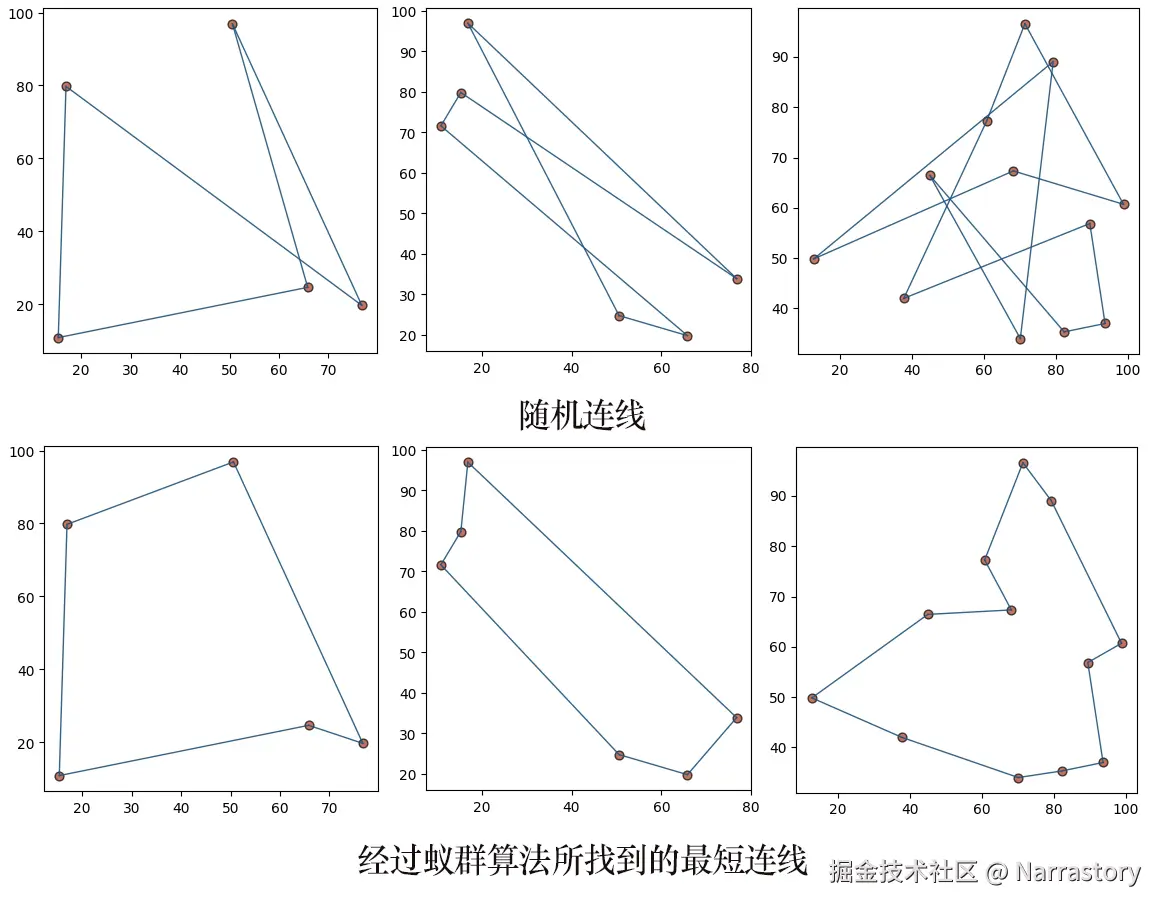
如果不借助蚁群算法这类智能优化方法，仅用传统算法来寻找上述问题的最优解，会非常困难。这是因为旅行商问题属于典型的NP-hard问题，其求解复杂度随着城市数量的增加而呈指数级爆炸

接下来就是蚁群算法的具体数学流程：

下面的公式和字母有点多，推荐你拿出草稿纸，在草稿纸上自己画画写写，手动的算一算。这种"手过一遍"的体验，会让抽象的概念变得清晰而牢固，更加深化你的理解。

假设平面中共有 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m个路径点（编号为 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 号点， 2 号点 , . . . , m 号点 1号点，2号点,...,m号点 </math>1号点，2号点,...,m号点），首先，随便选择一个点当做起点，然后在这个点放置 <math xmlns="http://www.w3.org/1998/Math/MathML"> n n </math>n个蚂蚁，这些蚂蚁将按照一定的规则，依次访问每一个点（不重复），最终回到起点。从起点出发、遍历所有点后返回起点的过程，称为一次迭代。

那么，蚂蚁如何决定下一步该前往哪个点呢？实际上，蚂蚁可不是乱走的，而是依据一个概率值 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i j P_{ij} </math>Pij来选择下一个访问的点。 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i j P_{ij} </math>Pij表示当前位于 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 号点的蚂蚁选择前往 <math xmlns="http://www.w3.org/1998/Math/MathML"> j j </math>j 号点的概率。如果 <math xmlns="http://www.w3.org/1998/Math/MathML"> j j </math>j 号点已经被当前蚂蚁访问过了，则 <math xmlns="http://www.w3.org/1998/Math/MathML"> P i j = 0 P_{ij} = 0 </math>Pij=0，否则概率由如下公式决定：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P i j = [ τ i j ( t ) ] α × [ 1 d i j ] β ∑ s ∈ { 未访问路径点集合 } [ τ i s ( t ) ] α × [ 1 d i s ] β P_{ij} = \frac{[\tau_{ij}(t)]^{\alpha} \times [\frac{1}{d_{ij}} ]^{\beta }}{\sum_{s\in \{ 未访问路径点集合 \}}^{} [\tau_{is}(t)]^{\alpha} \times [\frac{1}{d_{is}} ]^{\beta }} </math>Pij=∑s∈{未访问路径点集合}[τis(t)]α×[dis1]β[τij(t)]α×[dij1]β

看到这么一大坨公式不要慌，来慢慢分析，你就发现这个公式是非常的浅显直白。

  • <math xmlns="http://www.w3.org/1998/Math/MathML"> d i j d_{ij} </math>dij表示 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i点与 <math xmlns="http://www.w3.org/1998/Math/MathML"> j j </math>j点之间的直线距离，即两点间的路径长度；而 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 d i j \frac{1}{d_{ij}} </math>dij1就是距离的倒数，距离越短，该值越大；距离越长，该值越小。因此， <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 d i j \frac{1}{d_{ij}} </math>dij1 可以看作路径的"直观吸引力"：蚂蚁更倾向于前往距离较近的点。

  • <math xmlns="http://www.w3.org/1998/Math/MathML"> τ i j ( t ) \tau_{ij}(t) </math>τij(t)表明在第 <math xmlns="http://www.w3.org/1998/Math/MathML"> t t </math>t次迭代中，从 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i点到 <math xmlns="http://www.w3.org/1998/Math/MathML"> j j </math>j点的信息素浓度大小；

  • <math xmlns="http://www.w3.org/1998/Math/MathML"> α \alpha </math>α 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> β \beta </math>β 是两个重要的调节参数，分别控制信息素与距离对蚂蚁选择的影响权重。这两个参数需要人为设定：

    • 若 <math xmlns="http://www.w3.org/1998/Math/MathML"> α \alpha </math>α 较大，信息素的影响更强，蚂蚁更倾向于跟随之前蚂蚁留下的"气味轨迹"；
    • 若 <math xmlns="http://www.w3.org/1998/Math/MathML"> β \beta </math>β 较大，距离的影响更显著，蚂蚁会更偏向于选择距离较近的点。

通常，我们可以根据具体问题调整 <math xmlns="http://www.w3.org/1998/Math/MathML"> α \alpha </math>α 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> β \beta </math>β 的值，以平衡"探索"与"利用"的关系。例如，在算法初期可适当增大 <math xmlns="http://www.w3.org/1998/Math/MathML"> β \beta </math>β 以鼓励探索新路径；后期则可适当提高 <math xmlns="http://www.w3.org/1998/Math/MathML"> α \alpha </math>α 以利用已有的较优路径。

这样的话，这个公式是不是就非常清晰了，蚂蚁选择下一个点的概率，同时受到信息素浓度（集体经验）和距离倒数（局部启发）的影响 。分子部分表示路径 <math xmlns="http://www.w3.org/1998/Math/MathML"> i → j i \to j </math>i→j 的"综合吸引力"，分母则是对所有的未访问点的"综合吸引力"进行求和，确保概率之和为1。

让我们设想一个简单的场景：假设环境中只有 5 个路径点，当前一只蚂蚁位于 3 号点 ，并且它已经访问过了 5 号点 和 1 号点 。那么，它下一步前往这两个已访问点的概率为 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0，即：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P 31 = P 35 = 0 P_{31}= P_{35} = 0 </math>P31=P35=0

接下来，蚂蚁需要根据前面给出的概率公式，计算前往剩余未访问点（2 号点和 4 号点）的概率。假设算出的结果分别是：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> P 32 = 0.6 , P 34 = 0.4 P_{32} = 0.6,P_{34} = 0.4 </math>P32=0.6,P34=0.4

需要注意的是，这并不意味着蚂蚁下一步一定会前往 2 号点。实际上，算法会按照这两个概率值进行随机抽样，以此决定蚂蚁的实际移动方向。就好比掷一枚稍有偏重的骰子，虽然某一面朝上的可能性更大，但具体结果仍由随机抽取决定。

接下来详细讲解一下信息素浓度 <math xmlns="http://www.w3.org/1998/Math/MathML"> τ i j ( t ) \tau_{ij}(t) </math>τij(t)，由上文可知， <math xmlns="http://www.w3.org/1998/Math/MathML"> τ i j ( t ) \tau_{ij}(t) </math>τij(t)表明在第 <math xmlns="http://www.w3.org/1998/Math/MathML"> t t </math>t次迭代中，从 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i点到 <math xmlns="http://www.w3.org/1998/Math/MathML"> j j </math>j点路径上的信息素浓度；它是一个动态变化的量，在每次迭代结束后，都会按照以下规则进行更新：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> τ i j ( t + 1 ) = ( 1 − ρ ) τ i j ( t ) + ∑ k = 1 n p a s s Δ τ i j k \tau_{ij}(t+1) = (1-\rho )\tau_{ij}(t) + \sum_{k=1}^{n_{pass}} \Delta \tau_{ij}^{k} </math>τij(t+1)=(1−ρ)τij(t)+k=1∑npassΔτijk

我们来逐项分析这个更新过程。可以看到，下一次迭代中路径 <math xmlns="http://www.w3.org/1998/Math/MathML"> i → j i \to j </math>i→j 上的信息素浓度 <math xmlns="http://www.w3.org/1998/Math/MathML"> τ i j ( t + 1 ) \tau_{ij}(t+1) </math>τij(t+1) 由两部分构成：原有信息素的残留 与 本次迭代新增的信息素。

  • 信息素挥发 ： <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 1 − ρ ) τ i j ( t ) (1-\rho )\tau_{ij}(t) </math>(1−ρ)τij(t) 这里 <math xmlns="http://www.w3.org/1998/Math/MathML"> ρ \rho </math>ρ 信息素挥发系数，取值范围在 0 到 1 之间。它模拟了自然界中信息素随时间逐渐蒸发的现象。 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 1 − ρ ) (1-\rho ) </math>(1−ρ) 越小，说明信息素挥发得越快，历史信息对当前的影响就越弱；反之，则历史路径的影响力更持久。适当设置 <math xmlns="http://www.w3.org/1998/Math/MathML"> ρ \rho </math>ρ 可以避免算法过早陷入局部最优，也能让算法在后期聚焦于较优路径。
  • 信息素新增 ： <math xmlns="http://www.w3.org/1998/Math/MathML"> ∑ k = 1 n p a s s Δ τ i j k \sum_{k=1}^{n_{pass}} \Delta \tau_{ij}^{k} </math>∑k=1npassΔτijk 这一项代表了本次迭代中所有经过路径 <math xmlns="http://www.w3.org/1998/Math/MathML"> i → j i \to j </math>i→j 的蚂蚁所释放的信息素之和。其中：
  1. <math xmlns="http://www.w3.org/1998/Math/MathML"> n p a s s n_{pass} </math>npass 表示本次迭代中经过该路径的蚂蚁数量；
  2. <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ τ i j k \Delta \tau_{ij}^{k} </math>Δτijk 是第 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k 只蚂蚁在该路径上留下的信息素量，计算公式为：

<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> Δ τ i j k = Q L k \Delta \tau_{ij}^{k} = \frac{Q}{L_{k}} </math>Δτijk=LkQ

  1. <math xmlns="http://www.w3.org/1998/Math/MathML"> Q Q </math>Q 是一个人为设定的常数，代表每只蚂蚁携带的"信息素总量"；

  2. <math xmlns="http://www.w3.org/1998/Math/MathML"> L k L_k </math>Lk 是第 <math xmlns="http://www.w3.org/1998/Math/MathML"> k k </math>k 只蚂蚁在本次迭代中所走过路径的总长度。

这个设计非常直观：一只蚂蚁走过的路径越短（ <math xmlns="http://www.w3.org/1998/Math/MathML"> L k L_k </math>Lk 越小），它在各边上留下的信息素浓度就越高（ <math xmlns="http://www.w3.org/1998/Math/MathML"> Δ τ i j k \Delta \tau_{ij}^{k} </math>Δτijk 越大）。也就是说，更短的路径会获得更多的信息素增强 ，从而在后续迭代中吸引更多蚂蚁选择该路径。因此， <math xmlns="http://www.w3.org/1998/Math/MathML"> ∑ k = 1 n p a s s Δ τ i j k \sum_{k=1}^{n_{pass}} \Delta \tau_{ij}^{k} </math>∑k=1npassΔτijk 实际上就是对本次迭代中所有经过该路径的蚂蚁的"贡献"进行累加。

三. 代码实现

到此为止，蚁群算法的数学原理和核心流程我们已经梳理完毕。我知道，很多人（包括我自己）在初学蚁群算法时面对一连串的公式，都会感觉迷迷糊糊的。但请别担心！ 接下来，我们将暂时把公式放一放，通过编写代码来"感受"蚁群算法的运作。从构建问题场景、搭建算法骨架到最终迭代优化，我们将一步一步实现它。我相信，在你亲手实现了一遍蚁群算法后，再回过头去看那些数学公式，你就会豁然开朗，并将彻底理解蚁群算法。

3.1 实验环境搭建

在开始编写核心算法前，我们需要准备好两件事：一个待解决的路径问题 ，以及一套能让我们"看见"蚂蚁如何行走的可视化工具。这将极大帮助我们调试代码和理解算法行为。

下面的代码需要提前安装好 Python 的数据可视化库 matplotlib。可以使用 pip 进行安装：

bash 复制代码 
pip install matplotlib

首先，引入我们所需的工具库：

python 复制代码 
import random  # 用于生成随机数和随机操作
import math    # 用于数学计算，如开方求距离
import matplotlib.pyplot as plt  # 用于绘图，将路径可视化

创建虚拟城市（路径点）：我们随机生成一组二维坐标点来模拟不同的城市。

python 复制代码 
# 定义问题规模：有多少个城市（路径点）
points_size = 5
random.seed(42)  # 设定随机种子，确保结果可重复

# 随机生成城市的坐标 (x, y)
# random.uniform(a, b) 用于生成 [a, b) 区间内的随机浮点数
points_x = [random.uniform(0, 200) for _ in range(points_size)]
points_y = [random.uniform(0, 100) for _ in range(points_size)]

# 将坐标组合成点集，方便后续使用
# points[0] 是所有x坐标，points[1]是所有y坐标
points = [points_x, points_y]
print(points)

# === 输出 ===
[[127.89,   5.0, 55.01, 44.64, 147.29], 
 [ 67.67, 89.22,  8.69, 42.19, 2.98  ]]

points的每一列就是一个二维坐标，第一行是 <math xmlns="http://www.w3.org/1998/Math/MathML"> x x </math>x坐标，第二行是 <math xmlns="http://www.w3.org/1998/Math/MathML"> y y </math>y坐标；第1列就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 号点 0号点 </math>0号点，第2列就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 号点 1号点 </math>1号点,...

绘制城市位置图：将这些点的分布在图中绘制出来，如下图：

生成一条随机路径 ：为了理解什么是"一条路径"，我们首先生成一个随机的访问顺序（一个城市编号的排列）。随机生成一个访问序列的代码如下：

python 复制代码 
# 创建一个从0到4的列表，代表城市编号
lineSet = list(range(points_size))
# 随机打乱顺序，得到一条随机访问路径
random.shuffle(lineSet)
print(lineSet)

# === 输出 ===
[0, 4, 2, 3, 1]

lineSet表示一个访问序列 ，上面的输出的意思就是 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 号点 0号点 </math>0号点连接 <math xmlns="http://www.w3.org/1998/Math/MathML"> 4 号点 4号点 </math>4号点， <math xmlns="http://www.w3.org/1998/Math/MathML"> 4 号点 4号点 </math>4号点再连接 <math xmlns="http://www.w3.org/1998/Math/MathML"> 2 号点 2号点 </math>2号点，... （ <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 → 4 → 2 → 3 → 1 → 0 0 \to 4 \to 2 \to 3 \to 1 \to 0 </math>0→4→2→3→1→0）

现在，我们编写一个通用的可视化函数，它可以将任意给定的访问序列 lineSet 在城市点集 points 上画成一条闭合的回路。（不需要理解这个函数，只要会调用这个函数就行）

python 复制代码 
def drawLine(lineSet, points):
    fig, ax = plt.subplots(figsize=(5, 10), layout="tight")
    ax.scatter(points[0], points[1], s=30, c="#1d5380", edgecolor="black")
    for j, i in enumerate(lineSet):
        next_i = lineSet[0] if j == points_size - 1 else lineSet[j + 1]
        ax.plot(
            [points[0][i], points[0][next_i]],
            [points[1][i], points[1][next_i]],
            c="#a8381c",
            lw=1,
        )
    ax.set_aspect("equal")
    plt.show()

现在来尝试使用一下这个函数

python 复制代码 
# 传入之前的变量lineSet和points
drawLine(lineSet, points)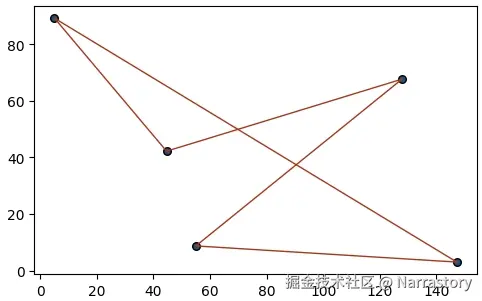

构建城市间距离矩阵 ：蚁群算法需要频繁计算城市间的距离。为了提高效率，我们预先计算好所有城市两两之间的距离，存储在一个矩阵中。这是一个对称矩阵，distance_matrix[i][j] 表示城市 i 到城市 j 的距离。

python 复制代码 
# 计算距离矩阵
# 初始化一个形状为 points_size × points_size 的零矩阵
distance_matrix = [[0.0] * points_size for _ in range(points_size)]

# 计算所有点对之间的距离
for i in range(points_size):
    for j in range(i + 1, points_size):  # 利用对称性，只计算上三角
        dx = points_x[i] - points_x[j]
        dy = points_y[i] - points_y[j]
        dist = math.sqrt(dx * dx + dy * dy)
        distance_matrix[i][j] = dist
        distance_matrix[j][i] = dist  # 对称赋值
print(distance_matrix)

# === 输出 ===
[[0.0, 124.77, 93.76, 87.06, 67.54],
 [124.77, 0.0, 94.79, 61.51, 166.38],
 [93.76, 94.79, 0.0, 35.07, 92.46],
 [87.06, 61.51, 35.07, 0.0, 109.88],
 [67.54, 166.38, 92.46, 109.88, 0.0]]

计算路径总长度的函数 ：有了距离矩阵，计算任意一条路径 lineSet 的总长度就非常高效了：只需按顺序累加相邻城市间的距离，最后加上从最后一个城市回到起点的距离。

下面的函数接收一个访问序列 lineSet，它能计算出这个访问序列的总长度。

python 复制代码 
def calculate_total_distance(lineSet):
    total = 0.0
    for i in range(points_size):
        start = lineSet[i]
        end = lineSet[(i + 1) % points_size]  # 取模实现环形连接
        total += distance_matrix[start][end]
    return total

# 测试一下这个函数
lineSetLength = calculate_total_distance(lineSet)
print(lineSetLength)

# === 输出 ===
501.1659747696346

3.2 蚁群算法实现

在开始编写代码之前，我们首先要明确蚁群算法中一个核心的数据结构：信息素矩阵 。这个矩阵通常是一个形状为 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( p o i n t s _ s i z e × p o i n t s _ s i z e ) (points\_size \times points\size) </math>(points_size×points_size) 的二维数组，记作 tauMatrix，其中第 <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 行第 <math xmlns="http://www.w3.org/1998/Math/MathML"> j j </math>j 列的元素 <math xmlns="http://www.w3.org/1998/Math/MathML"> τ i j \tau{ij} </math>τij 表示在路径 <math xmlns="http://www.w3.org/1998/Math/MathML"> i → j i \to j </math>i→j 上的信息素浓度。

我们通常会给所有路径赋予一个初始信息素值，这里设为 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0.5 0.5 </math>0.5，即：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> τ i j ( 0 ) = 0.5 , ( i ≠ j ) \tau_{ij}(0) = 0.5 ,\space (i \ne j) </math>τij(0)=0.5, (i=j)

这里注意：信息素初始值不能设为 0，你可以思考一下为什么不能设置为 0。

在代码中，我们用一个二维列表来表示信息素矩阵，并且规定城市到自身的路径信息素为 0（因为不需要走自己到自己的路）：

python 复制代码 
tauMatrix = [
    [0 if i == j else 0.5 for j in range(points_size)] for i in range(points_size)
]
print(tauMatrix)

# === 输出 ===
[[0, 0.5, 0.5, 0.5, 0.5],
 [0.5, 0, 0.5, 0.5, 0.5],
 [0.5, 0.5, 0, 0.5, 0.5],
 [0.5, 0.5, 0.5, 0, 0.5],
 [0.5, 0.5, 0.5, 0.5, 0]]

下面，我们定义蚁群算法的几个关键超参数。这些参数直接影响蚂蚁的搜索行为与算法的收敛特性：

python 复制代码 
alpha = 1      # 信息启发因子，控制信息素的重要性（对应公式中的 α）
beta = 1       # 期望启发因子，控制距离的重要性（对应公式中的 β）
ants_num = 40  # 每轮迭代中蚂蚁的数量（对应公式中的 n）
epochs = 60    # 迭代次数（算法运行的轮数）
ro = 0.25      # 信息素挥发系数（对应公式中的 ρ）
Q = 10         # 信息素强度常数，表示一只蚂蚁在一轮中释放的信息素总量

3.2.1 一只蚂蚁的行走

有了前面的基础，我们现在进入算法的核心环节：一只蚂蚁 如何根据信息素和距离信息，逐步构建出一条完整的访问路径。这个过程的实现就是下面这个build_ant_path函数。

让我先把它展示出来，然后我们一步一步拆解它的工作原理：

python 复制代码 
def build_ant_path(tau_matrix, start_city=0):
    """
    单只蚂蚁构建完整路径
    参数：
        tau_matrix: 当前信息素矩阵
        start_city: 起点城市编号（默认为0号点）
    返回：蚂蚁的完整访问序列
    """
    # 初始化：从起点开始，标记起点为已访问
    current_city = start_city
    visited = [False] * points_size
    visited[start_city] = True
    path = [start_city]

    # 逐步选择下一个城市，直到访问完所有城市
    while len(path) < points_size:
        # 获取当前未访问的城市列表
        unvisited_cities = [i for i in range(points_size) if not visited[i]]

        # 计算前往每个未访问城市的概率
        probabilities = []
        for next_city in unvisited_cities:
            tau = tau_matrix[current_city][next_city]  # 信息素浓度
            eta = (
                1.0 / distance_matrix[current_city][next_city]
            )  # 距离倒数（启发式信息）
            attraction = (tau**alpha) * (eta**beta)  # 综合吸引力
            probabilities.append(attraction)

        # 概率归一化（使所有概率之和为1）
        total = sum(probabilities)
        probabilities = [p / total for p in probabilities]

        # 轮盘赌选择：根据概率随机选择下一个城市
        rand = random.random()
        cumulative = 0.0
        selected_city = None

        for i, prob in enumerate(probabilities):
            cumulative += prob
            if rand <= cumulative:
                selected_city = unvisited_cities[i]
                break

        # 确保选到了城市（安全机制）
        if selected_city is None:
            selected_city = unvisited_cities[-1]

        # 移动到选中的城市
        path.append(selected_city)
        visited[selected_city] = True
        current_city = selected_city

    return path

看起来代码有点长，但别担心！这其实就是一个模拟一只蚂蚁走路的过程，我们一点一点来看：

第一步：初始化蚂蚁的"记忆"

蚂蚁出发前需要记住两件事：

  1. 自己当前在哪个城市 ：用current_city记录
  2. 哪些城市已经去过了 ：用visited列表记录（True表示已访问）
  3. 已经走过的路径 ：用path列表记录访问顺序
python 复制代码 
current_city = start_city
# 创建一个长度为points_size的全False数组
visited = [False] * points_size	
visited[start_city] = True
path = [start_city]

初始化后，蚂蚁站在起点，起点标记为"已访问"，路径记录中只有起点自己。

第二步：循环选择下一个城市

蚂蚁需要依次访问所有城市，所以用一个while循环，直到已访问的路径长度等于城市数量：

python 复制代码 
while len(path) < points_size:

第三步：找出所有"可去"的城市

蚂蚁不能重复访问已经去过的城市，所以要先找出所有还没去过的城市：

python 复制代码 
unvisited_cities = [i for i in range(points_size) if not visited[i]]

第四步：计算前往每个城市的"吸引力"

这是算法的核心！对于每个未访问城市，蚂蚁要计算它的"综合吸引力"：

python 复制代码 
for next_city in unvisited_cities:
    tau = tau_matrix[current_city][next_city]  # 信息素浓度
    eta = 1.0 / distance_matrix[current_city][next_city]  # 距离倒数
    attraction = (tau**alpha) * (eta**beta)  # 综合吸引力
    probabilities.append(attraction)

这三行代码其实就是我们前面概率公式的分子部分：

  • tau：当前路径上的信息素浓度
  • eta：距离的倒数（距离越近，eta越大）
  • attraction：将信息素和距离信息结合起来的综合吸引力

第五步：概率归一化

现在probabilities列表中存储的是每个未访问城市的"吸引力"，但这些值还不是概率。我们需要把它们变成真正的概率值（所有概率之和为1）：

python 复制代码 
total = sum(probabilities)
probabilities = [p / total for p in probabilities]

这步操作相当于我们公式中的分母部分：把所有未访问城市的吸引力加起来作为总和，然后用每个城市的吸引力除以这个总和。

第六步：抽样

现在每个城市都有了被选择的概率，但具体选哪个呢？我们不能简单地选概率最大的，那样就失去了随机性。这里用到了经典的轮盘赌选择法。

想象一个转盘，每个城市按照概率大小占据转盘的一块扇形区域。然后我们转动转盘，指针停在哪块就选择哪个城市。

代码实现是这样的：

python 复制代码 
rand = random.random()  # 生成一个0-1的随机数
cumulative = 0.0  # 累积概率
selected_city = None

# 从第一个城市开始累加概率
for i, prob in enumerate(probabilities):
    cumulative += prob
    if rand <= cumulative:  # 随机数落在了当前城市的概率区间内
        selected_city = unvisited_cities[i]
        break

为什么叫"轮盘赌"？你可以这样理解：

  • 假设有三个城市A、B、C，概率分别是0.2、0.3、0.5
  • 那么转盘上A占20%的面积，B占30%，C占50%
  • 生成一个0-1的随机数，如果在0-0.2之间选A，0.2-0.5之间选B，0.5-1.0之间选C

第七步：安全机制和状态更新

有时候因为浮点数精度问题，随机数可能略大于1（虽然极少发生），这时候需要兜底：

python 复制代码 
if selected_city is None:
    selected_city = unvisited_cities[-1]  # 选最后一个未访问城市

选定城市后，更新蚂蚁的状态：

python 复制代码 
path.append(selected_city)  # 将选中的城市加入路径
visited[selected_city] = True  # 标记为已访问
current_city = selected_city  # 蚂蚁移动到新城市

就这样循环往复，直到这只蚂蚁访问完所有城市后，最后函数返回这只蚂蚁的访问序列数组。

3.2.2 信息素更新

我们前面提到，信息素矩阵不是一成不变的。在每一轮迭代结束后，所有蚂蚁都完成了自己的探索，它们所经过的路径上都会留下新的信息素。这时，我们就需要根据这一轮蚂蚁们的行走轨迹来更新地图上的"气味"------也就是信息素矩阵。这正是我们下面这个函数update_pheromone_matrix的核心任务：

这个函数的完整代码如下：（相信你看注释就能看懂）

如果暂时不能理解，可以先看3.2.3 蚁群算法主框架，在了解整个框架后，再回来看下面这个函数可能会更好理解一些。

python 复制代码 
def update_pheromone_matrix(tau_matrix, all_paths, all_lengths):
    """
    更新信息素矩阵
    规则：先挥发，再根据蚂蚁路径新增信息素
    参数：
        tau_matrix: 当前信息素矩阵，存储着上一轮留下的"集体经验"。
        all_paths: 一个列表，存储了本轮所有蚂蚁走过的访问序列。
                    例如：[[0,2,1,4,3], [3,0,4,1,2], ...]
        all_lengths: 一个列表，存储了与all_paths对应的每条路径的总长度。
                    例如：[501.16, 488.32, ...]
    返回：更新后的信息素矩阵，它将作为下一轮蚂蚁决策的"新地图"。
    """
    # 第一部分：信息素挥发 - "忘记"一部分旧经验
    for i in range(points_size):
        for j in range(points_size):
            if i != j:  # 跳过对角线，因为蚂蚁不需要从城市走到自己。
                # 这是公式中的 (1-ρ) * τ_ij(t) 部分
                tau_matrix[i][j] = (1 - ro) * tau_matrix[i][j]
    # 到这一步，矩阵中每条边上的信息素都"蒸发"掉了一部分（ro比例）。
    # 这非常重要！它模拟了气味随时间消散的自然现象，防止老旧、可能不好的"经验"
    # 过度积累，让算法有机会探索新路径，避免过早陷入死胡同。

    # 第二部分：信息素新增 - 根据本轮表现"奖励"好路径
    for ant_idx in range(len(all_paths)): # 遍历本轮每一只蚂蚁
        path = all_paths[ant_idx]          # 获取第ant_idx只蚂蚁的访问序列
        path_length = all_lengths[ant_idx]  # 获取这只蚂蚁走的总路程
        # 计算这只蚂蚁在它经过的每条边上应该释放多少信息素
        # 这就是公式中的 Δτ_ij^k = Q / L_k
        delta_tau = Q / path_length         

        # 这只蚂蚁是如何连接城市的？我们来复原它走过的每一条"边"
        for i in range(points_size):
            start_city = path[i] # 边的起点城市编号
            # 边的终点城市编号。注意：当i是最后一个城市时，下一个要连回起点。
            end_city = path[(i + 1) % points_size] 

            # 在这条边（从start_city到end_city）上增加信息素
            tau_matrix[start_city][end_city] += delta_tau
            # 同时，在反方向（从end_city到start_city）也增加同样的信息素
            tau_matrix[end_city][start_city] += delta_tau
            # 为什么要更新两边？因为我们的地图是无向的。
            # 从A到B的路和从B到A是同一条物理路径，其"吸引力"应该是一致的。
            # 这确保了信息素浓度的对称性，与我们的对称距离矩阵相匹配。

    # 现在，信息素矩阵已经完成了"挥发+新增"的完整更新。
    # 短路径因为得到了更多、更浓的"奖励"（delta_tau更大），
    # 其对应边上的信息素浓度会显著高于长路径。
    return tau_matrix

有了这个函数，我们就可以在每一轮迭代结束后，用本轮所有蚂蚁探索的结果去修正全局的"经验地图"---信息素矩阵，从而引导下一轮的蚂蚁们更有希望找到更优的路径。

3.2.3 蚁群算法主框架

至此，我们已经学习了解了蚁群算法的各个核心组件。现在，让我们把这些"零件"组装起来，看看整个算法是如何运行的。下面就是我们要讲解的ant_colony_optimization函数。

这个函数协调上面的所有组件，最后运算完成后，返回一个最优访问序列。

我这里也就不再解释什么了，下面👇的代码已经说的非常清楚明白了。

python 复制代码 
def ant_colony_optimization():
    """
    蚁群算法主框架
    返回：全局最优访问序列
    """
    # 1. 初始化信息素矩阵
    tau_matrix = tauMatrix

    # 2. 初始化全局最优记录
    global_best_path = None
    # 我们设立一个目标"要找的最短路径"的长度，但不知道有多短，所以先把目标设为"无穷大"（float("inf")）
    global_best_length = float("inf")

    # 3. 主迭代循环 - 团队的多次试错与学习
    for epoch in range(epochs):
        # 3.1 本次迭代中所有蚂蚁的路径和长度
        all_paths = []
        all_lengths = []

        # 3.2 让每只蚂蚁构建路径，每一次迭代共ants_num只蚂蚁（前文已经定义过）
        for _ in range(ants_num):
            # 单只蚂蚁构建完整路径
            ant_path = build_ant_path(tau_matrix, start_city=0)
            # 计算该路径长度
            path_length = calculate_total_distance(ant_path)

            # 存储路径和长度
            all_paths.append(ant_path)
            all_lengths.append(path_length)

            # 3.3 更新全局最优
            if path_length < global_best_length:
                global_best_length = path_length
                global_best_path = ant_path.copy()
                # 注意：这里使用了.copy()方法，这是因为Python中列表是可变对象。如果不复制，直接赋值global_best_path = ant_path，那么当ant_path在后面被修改时，global_best_path也会被修改。.copy()创建了一个独立的副本。

        # 3.4 更新信息素矩阵
        tau_matrix = update_pheromone_matrix(tau_matrix, all_paths, all_lengths)

    return global_best_path

最后调用这个函数，再用drawLine函数可视化一下：

python 复制代码 
# 执行蚁群算法
best_path = ant_colony_optimization()

# 输出最优路径
print("最优访问序列:", best_path)
print("路径总长度:", calculate_total_distance(best_path))

# 绘制最优路径
drawLine(best_path, points)

# === 输出 ===
最优访问序列: [0, 4, 2, 3, 1]
路径总长度: 381.33365765496677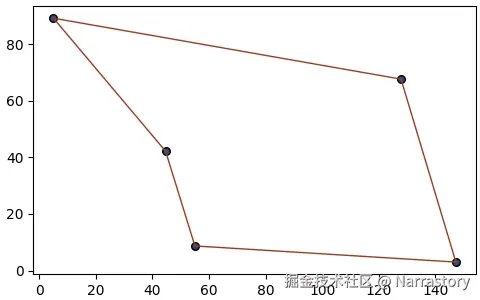

四. 结语

以上就是蚁群算法的完整介绍与实现过程。如果你是初学者，能够坚持读到这里，真是非常不容易，这也说明了你已经对蚁群算法有了非常深刻的理解，值得为自己点个赞👍！

当然了，由于是演示程序，上面的代码效率绝对不是最优的，但是足够清晰了；在实际应用中，如果结合 numpy 这样的科学计算库，通常只需要五十行左右的代码就能高效地实现蚁群算法。numpy 基于向量化运算，底层由 C 语言实现，能大幅提升数值计算的性能------深入学习之后，你甚至可以写出效率接近 C 语言的 Python 实现。因此，如果你计划继续从事算法开发或数据分析，掌握 numpy 会是一个非常值得投入的方向（本文为照顾 Python 初学者，特意使用了纯 Python 列表实现，方便理解每一步的过程）。

最后，如果你喜欢这种"从数学原理到代码实现"的讲解风格，可以关注我哦(✧◡✧)！，我会持续分享更多类似的内容～

也欢迎在评论区留言，告诉我你想了解的其他算法、技术方向，或是全栈开发相关的话题。你的反馈将成为我创作下一篇教程的重要动力！

相关推荐
mit6.8242 小时前
八皇后变题hash|网格dp
算法
bybitq2 小时前
LeetCode-437-路径总和3
算法
鱼跃鹰飞2 小时前
Leetcode尊享面试100题：1060. 有序数组中的缺失元素
算法·leetcode·面试
啊我不会诶2 小时前
AtCoder Beginner Contest 438 vp补题
算法
computersciencer2 小时前
用最小二乘法求解一元一次方程模型的参数
算法·机器学习·最小二乘法
mit6.8243 小时前
扫描线|离散化|seg+二分|卡常
算法
不穿格子的程序员3 小时前
从零开始写算法——二叉树篇6:二叉树的右视图 + 二叉树展开为链表
java·算法·链表
大志若愚YYZ3 小时前
ROS2学习 C++中的this指针
c++·学习·算法
AI科技星3 小时前
光子的几何起源与量子本质：一个源于时空本底运动的统一模型
服务器·人工智能·线性代数·算法·机器学习
热门推荐
01GitHub 镜像站点02Linux下V2Ray安装配置指南03Labelme从安装到标注：零基础完整指南04Claude Code Skills 实用使用手册05AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南06UV安装并设置国内源072025年大语言模型技术全景报告08网站改了域名，如何查找？09安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）10在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）