算法刷题--哈希表

文章目录

• • [1、242 有效的字母异位词](#1、242 有效的字母异位词)
  • [2、383 赎金信](#2、383 赎金信)
  • [3、 438 找到字符串中所有字母异位词](#3、 438 找到字符串中所有字母异位词)
  • • 滑动窗口的核心机制
    • • 第一步：窗口扩张（右边界进入）
      • 第二步：寻找窗口起始点
      • 第三步：判定异位词（核心匹配）
      • 第四步：窗口收缩（左边界移出）
    • 逻辑全过程模拟
    • 优化版
  • [4、 349 两个数组的交集](#4、 349 两个数组的交集)
  • • [1. 数组模拟哈希表（最常用、最快）](#1. 数组模拟哈希表（最常用、最快）)
    • [2. 自己手动实现哈希表 (Hash Table)](#2. 自己手动实现哈希表 (Hash Table))
    • [3. 使用第三方库（工程实践中常用）](#3. 使用第三方库（工程实践中常用）)
    • [4. 排序 + 二分查找 (模拟 Set/Map)](#4. 排序 + 二分查找 (模拟 Set/Map))
    • 总结与建议
  • [349 另解 c语言实现](#349 另解 c语言实现)
  • • [方法一：排序 + 双指针（最推荐，面试常考）](#方法一：排序 + 双指针（最推荐，面试常考）)
    • [方法二：排序 + 二分查找](#方法二：排序 + 二分查找)
    • [方法三：使用 `uthash` 库（模拟真正的 Set/Map）](#方法三：使用 uthash 库（模拟真正的 Set/Map）)
    • [1. 核心结构体定义](#1. 核心结构体定义)
    • [2. 初始化与内存准备](#2. 初始化与内存准备)
    • [3. 第一步：构建哈希表（去重存入）](#3. 第一步：构建哈希表（去重存入）)
    • [4. 第二步：寻找交集（并防止结果重复）](#4. 第二步：寻找交集（并防止结果重复）)
    • [5. 第三步：善后工作（内存回收）](#5. 第三步：善后工作（内存回收）)
    • 总结：这段代码的精妙之处
    • 三种方法对比
  • [5、 350 两个数组的交集②](#5、 350 两个数组的交集②)
  • [6、202 快乐数](#6、202 快乐数)
  • [7、1 两数之和](#7、1 两数之和)
  • [8、454 四数相加](#8、454 四数相加)
  • • [1. 为什么会溢出？](#1. 为什么会溢出？)
    • [2. 如何修正？（最务实的两种方法）](#2. 如何修正？（最务实的两种方法）)
    • • [**方法 A：使用 `long` 或 `long long`（推荐）**](#方法 A：使用 long 或 long long（推荐）)
      • [**方法 B：针对 `uthash` 的特化修正**](#方法 B：针对 uthash 的特化修正)
    • [💡 核心知识点补充](#💡 核心知识点补充)
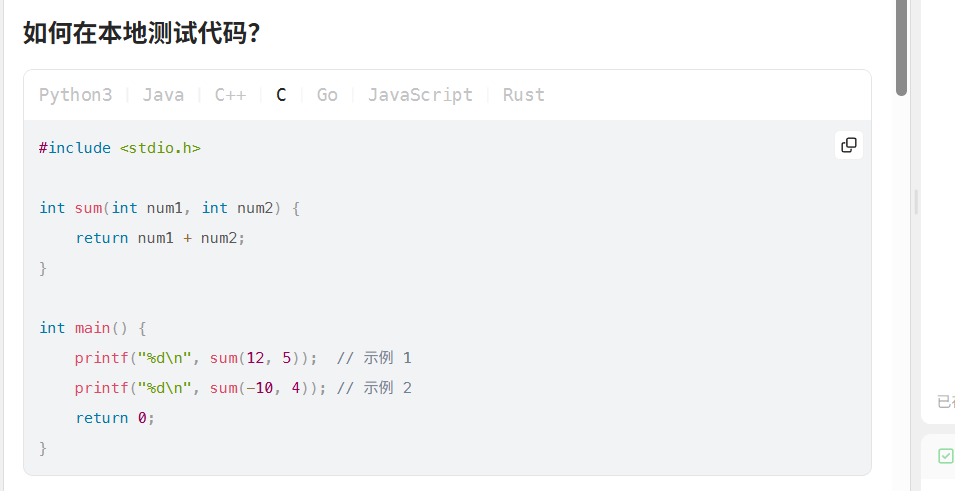
  • [杂记 如何在本地测试代码](#杂记 如何在本地测试代码)

当我们遇到了要快速判断一个元素是否出现集合里的时候，就要考虑哈希法。
但是哈希法也是牺牲了空间换取了时间，因为我们要使用额外的数组，set或者是map来存放数据，才能实现快速的查找。
如果在做面试题目的时候遇到需要判断一个元素是否出现过的场景也应该第一时间想到哈希法！

1、242 有效的字母异位词

题目

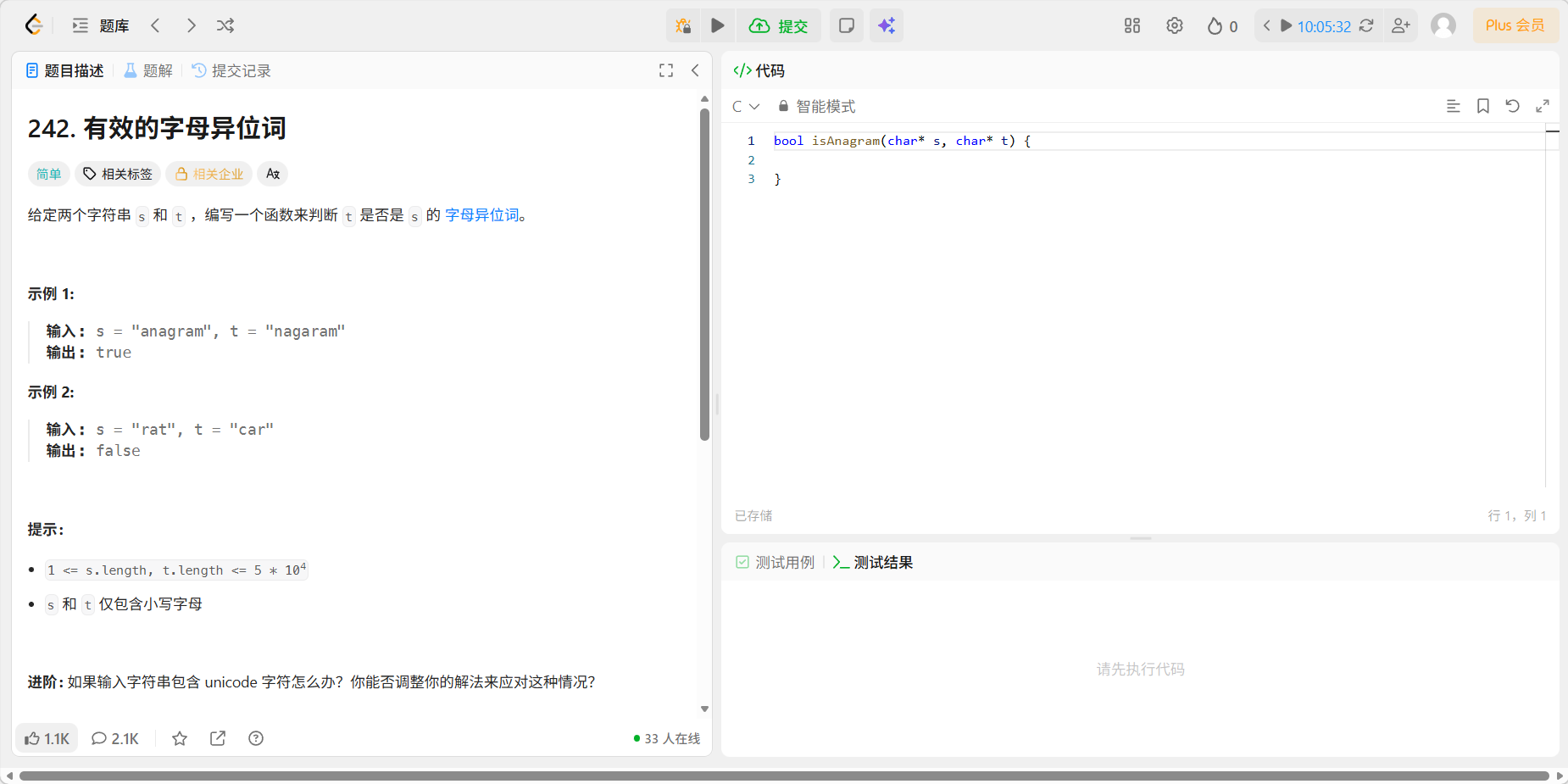
代码

数组其实就是一个简单哈希表

先通过strlen计算出两个字符串的长度，然后判断二者是否相等，不相等则返回false，然后申请一个大小为26的数组freq初始化为0，先用于记录字符串s中每一个小写字母的出现频率，freq[i-'a']++；

然后再遍历t字符串中的每一个字符，freq[i-'a']--; 最后再判断freq数组中元素是不是都为0，若不是则返回false，否则返回true。

bool isAnagram(char* s, char* t) {
    int a = strlen(s);
    int b = strlen(t);
    if(a != b){
        return false;
    }
    int freq[26] = {0};
    for(int i = 0;i < a;i++){
        freq[s[i]-'a']++;
    }
    for(int i = 0;i < b;i++){
        freq[t[i]-'a']--;
    }
    for(int i = 0;i< 26;i++){
        if(freq[i] != 0){
            return false;
        }
    }
    return true;
}

时间复杂度：O(n)

空间复杂度：O(1)
另解：使用qsort和strcmp

int cmp(const void* _a,const void* _b){
    char a = *(char*)_a,b = *(char*)_b;
    return a-b;
}
bool isAnagram(char* s, char* t) {
    int a = strlen(s);
    int b = strlen(t);
    if(a != b){
        return false;
    }
    qsort(s,a,sizeof(char),cmp);
    qsort(t,b,sizeof(char),cmp);
    return strcmp(s,t) == 0;
}

时间复杂度：O(nlogn)

空间复杂度：O(nlogn)

2、383 赎金信

题目

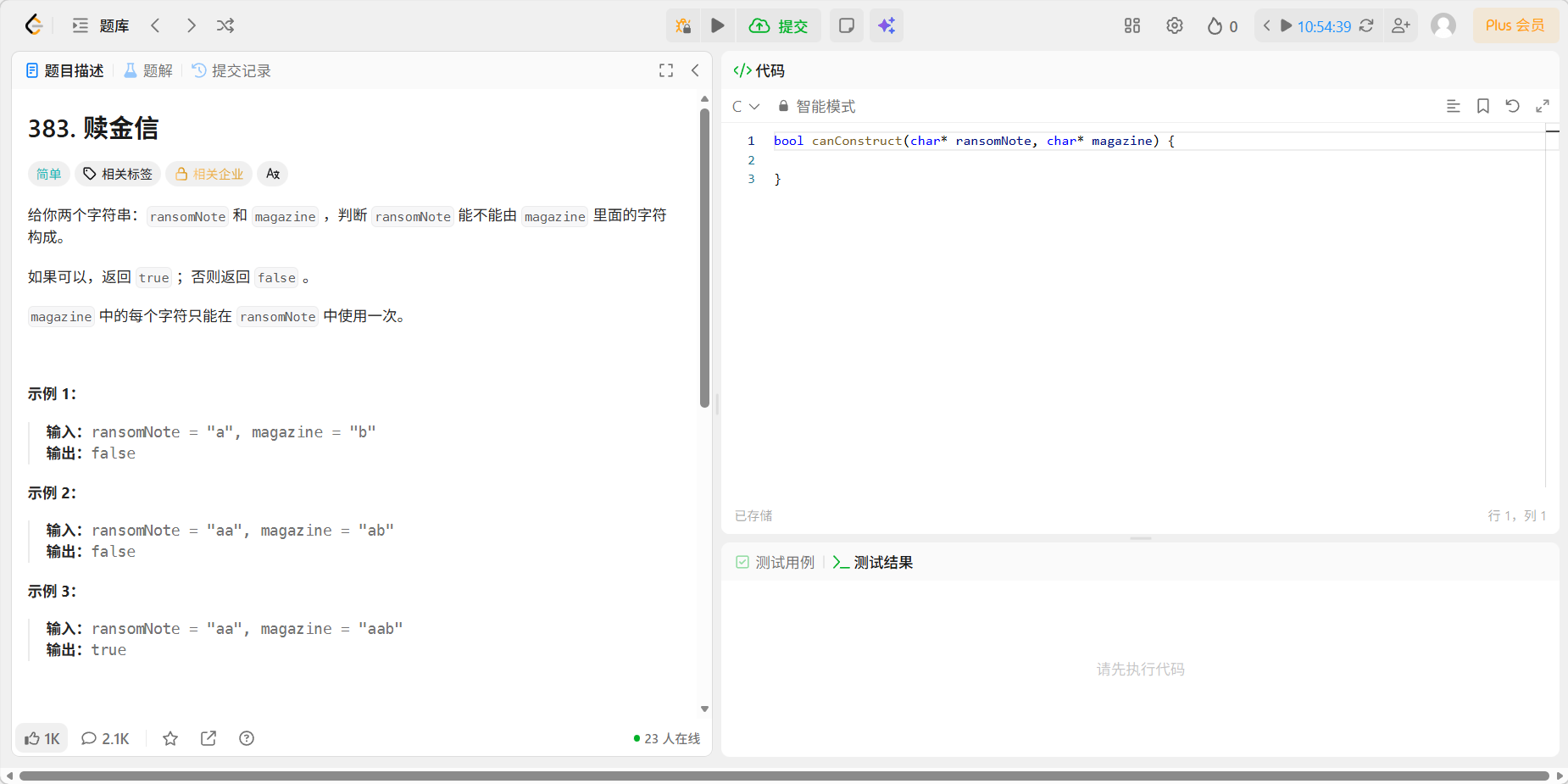
代码

因为限制了数的范围小于等于1000，所以可以使用跟第一题一样的思路，用数组模拟哈希~

bool canConstruct(char* ransomNote, char* magazine) {
    int a = strlen(ransomNote);
    int b = strlen(magazine);
    if(a > b){
        return false;
    }
    int hash[26] = {0};
    for(int i = 0;i < b;i++){
        hash[magazine[i]-'a']++;
    }
    for(int i = 0;i < a;i++){
        hash[ransomNote[i]-'a']--;
    }
    for(int i = 0;i < 26;i++){
        if(hash[i] < 0){
            return false;
        }
    }
    return true;
}

时间复杂度：O(n)

空间复杂度：O(1)

3、 438 找到字符串中所有字母异位词

题目

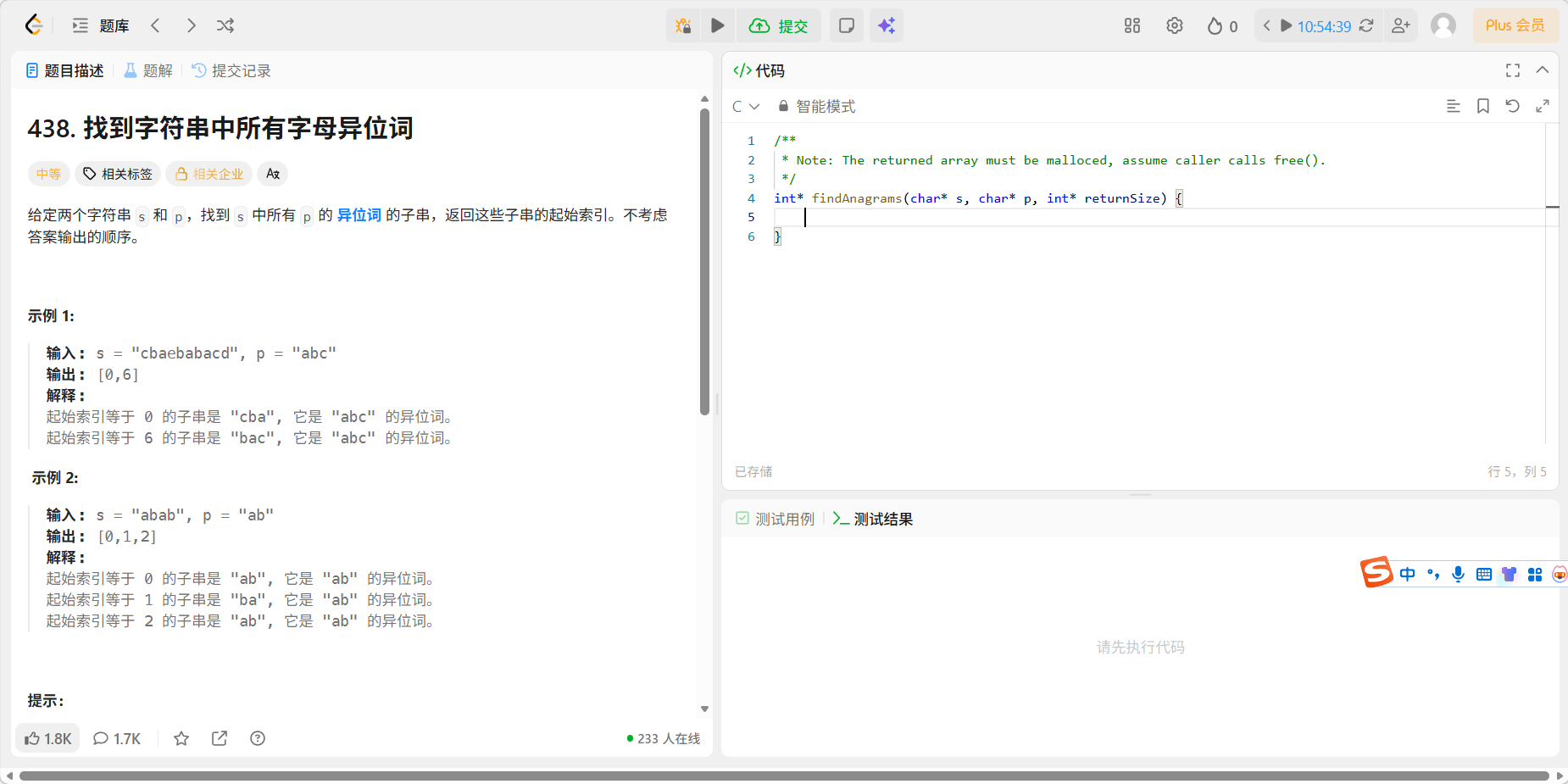
代码

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* findAnagrams(char* s, char* p, int* returnSize) {
    int a = strlen(p);
    int b = strlen(s);
    *returnSize = 0;
    if(b < a){
        return NULL;
    }
    int* ans = (int*)malloc(sizeof(int)*b);
    //int* ans = (int*)calloc(b,sizeof(int));
    int cnt_p[26] = {0};
    int cnt_s[26] = {0};
    for(int i = 0;i < a;i++){
        cnt_p[p[i]-'a']++;
    }
    
    for(int i = 0;i < b;i++){
        cnt_s[s[i]-'a']++;
        int j = i+1-a;
        if(j < 0){
            continue;
        }
        if(memcmp(cnt_p,cnt_s,sizeof(cnt_p)) == 0){
            ans[(*returnSize)++] = j;
        }
        cnt_s[s[j]-'a']--;
    }
    return ans;
}

滑动窗口（Sliding Window） 算法，用来解决字符串匹配类问题。它的核心逻辑是：维护一个固定长度为 strlen(p) 的窗口，像扫描仪一样扫过字符串 s。

滑动窗口的核心机制

这段 for 循环是整个算法的灵魂，它同时完成了窗口的扩张、收缩和判定。

第一步：窗口扩张（右边界进入）

cnt_s[s[i]-'a']++;

• 不管三七二十一，先把当前字符 s[i] 加入窗口的统计数组 cnt_s 中。

第二步：寻找窗口起始点

int j = i + 1 - a;
if(j < 0){
    continue; // 窗口长度还没达到 a，继续扩张
}

• a 是字符串 p 的长度。
• 当 i 增加到 a-1 时，窗口长度第一次达到 a，此时 j = 0。

第三步：判定异位词（核心匹配）

if(memcmp(cnt_p, cnt_s, sizeof(cnt_p)) == 0){
    ans[(*returnSize)++] = j;
}

• memcmp ：比较两个频率数组。如果内容完全一样，说明当前窗口 s[j...i] 是 p 的一个异位词。
• 记录索引 ：把起始位置 j 存入结果数组。

第四步：窗口收缩（左边界移出）

cnt_s[s[j]-'a']--;

• 这是为了下一次循环做准备。
• 窗口右移一位时，左边的字符 s[j] 就不在窗口里了，必须从统计数组中减去。

---

逻辑全过程模拟

假设 s = "cbaebabacd", p = "abc" (长度为 3)：

1. i=0,1 : 窗口在扩张，cnt_s 记录了 'c', 'b'。
2. i=2 : 窗口长度达标（3）。此时窗口是 "cba"。

• cnt_s 为 {a:1, b:1, c:1}。
• 对比 cnt_p 成功！记录索引 0。
• 减去 s[0] ('c')，cnt_s 变为 {a:1, b:1, c:0}。

3. i=3 : 窗口右移，加入 'e'。此时窗口变为 "bae"。

• 对比 cnt_p 失败。
• 减去 s[1] ('b')，cnt_s 变为 {a:1, b:0, c:0, e:1}。

4. ...以此类推，直到扫完整个字符串。

---

时间复杂度：O(n)

空间复杂度：O(1)

优化版

核心思想：动态平衡计数器代码不再使用两个数组对比，而是只用一个 cnt 数组。 初始状态：cnt 存的是 p 中每个字母的"欠账"。比如

p 是 "abc"，那么 cnt['a']=1, cnt['b']=1, cnt['c']=1。 右端进窗：当 s[right]

进入窗口，它会执行 cnt[c]--。这意味着"还掉"了一个欠账。 核心准则：只要 cnt[c] 保持 ≥ 0 \ge 0 ≥0，说明当前窗口内的字符 c 的数量没有超过 p 中该字符的总数。

代码

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* findAnagrams(char* s, char* p, int* returnSize) {
    int n = 0;
    int cnt[26] = {0};
    for(;p[n];n++){
        cnt[p[n]-'a']++;
    }
    int* ans = (int*)calloc(strlen(s),sizeof(int));
    *returnSize = 0;
    int j = 0;
    for(int i = 0;s[i];i++){
        int c = s[i]-'a';
        cnt[c]--;
        while(cnt[c] < 0){
            cnt[s[j]-'a']++;
            j++;
        }
        if(i-j+1 == n){
            ans[(*returnSize)++] = j;
        }
    }
    return ans;
}

时间复杂度：O(m+n)，其中 m 是 s 的长度，n 是 p 的长度。虽然写了个二重循环，但是内层循环中对 left 加一的总执行次数不会超过 m 次，所以滑窗的时间复杂度为 O(m)。

空间复杂度：O(∣Σ∣)，其中 ∣Σ∣=26 是字符集合的大小。返回值不计入

4、 349 两个数组的交集

题目

代码

暴力解，用数组模拟哈希表，跟第三题类似，定义两个数组初始化为0，然后如果有其中的元素就加一，最后再判断两个数组的n是不是都大于0，是则把n记录即可

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* intersection(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
    int n = 0;
    int cnt_1[1001] = {0};
    int cnt_2[1001] = {0};
    int a = (nums1Size > nums2Size) ? nums1Size : nums2Size;
    int* ans = (int*)malloc(sizeof(int)*a);
    *returnSize = 0;
    for(n = 0;n < nums1Size;n++){
        cnt_1[nums1[n]]++;
    }
    for(n = 0;n < nums2Size;n++){
        cnt_2[nums2[n]]++;
    }
    for(n = 0;n < 1001;n++){
        if(cnt_1[n] != 0&&cnt_2[n] != 0){
            ans[(*returnSize)++] = n;
        }
    }
    return ans;
}

时间复杂度：O(n)

空间复杂度：O(1) or O(1001)

突然发现c语言中没有set和map！

这是一个非常经典的问题。C 语言标准库（Standard Library）中没有原生的 set 或 map。

在 C++ 中，你有 STL（如 std::set 和 std::map）；在 Java 中，你有 HashMap；但在 C 语言中，标准库的设计哲学是"极简"，它只提供了最基础的输入输出、字符串处理和数学运算。

针对你的疑问，我整理了在 C 语言中处理这种情况的几种常见方案：

---

1. 数组模拟哈希表（最常用、最快）

就像你之前写 isAnagram 题目时用 int freq[26] 一样，如果你的 Key（键）范围是已知且有限的（例如小写字母、ASCII 码、或较小的整数），这是最佳选择。

• 优点：速度极快 ()，内存连续，极其简单。
• 缺点：只能处理范围固定的整型 Key，无法处理字符串或其他复杂类型。

---

2. 自己手动实现哈希表 (Hash Table)

如果你需要处理的是字符串作为 Key，通常需要自己写一套逻辑：

1. 定义结构体：存储键值对和链表指针（处理冲突）。
2. 编写哈希函数 ：比如著名的 DJB2 或 BKDR 算法，将字符串转为整数索引。
3. 处理冲突：通常使用"拉链法"（数组 + 链表）。

---

3. 使用第三方库（工程实践中常用）

如果你在做实际的项目（而不是在做 LeetCode 刷题），通常不会从零手写，而是引入成熟的开源宏或库：

• uthash ：这是一个非常神奇的 C 语言库，它只有一个头文件 (uthash.h) 。你只需要在你的结构体里加一个 UT_hash_handle，就能像用 Map 一样操作任何结构体。

struct my_struct {
    int id;            /* key */
    char name[10];
    UT_hash_handle hh; /* 让这个结构体可哈希 */
};

• GLib (GHashTable)：这是 Linux 开发（如 GNOME 桌面）中极其常用的库，功能非常接近高级语言的 Map。

---

4. 排序 + 二分查找 (模拟 Set/Map)

如果你不需要频繁地插入数据，只是为了查询：

1. 把所有数据存入数组。
2. 使用 qsort 进行排序。
3. 使用 bsearch（C 标准库自带）进行二分查找。

• 这种方法在某种程度上能起到 有序 Set 的作用。

---

总结与建议

场景	推荐方案
LeetCode 简单字符/数字题	数组模拟 (如 cnt[256])
需要处理大量字符串键	手动实现简单哈希表 或使用 uthash
需要数据自动有序	排序数组 + 二分查找
高级工程项目	GLib 或其他成熟的算法库

349 另解 c语言实现

方法一：排序 + 双指针（最推荐，面试常考）

这种方法不需要任何额外的哈希表空间，空间复杂度为 （如果不算返回结果所需的空间）。

核心逻辑：

1. 对两个数组进行升序排序。
2. 使用两个指针 i 和 j 分别指向两个数组的起始位置。
3. 比较 nums1[i] 和 nums2[j]：

• 如果相等：存入结果（注意判断是否与结果中上一个元素重复），然后 i++, j++。
• 如果 nums1[i] < nums2[j]：i++。
• 如果 nums1[i] > nums2[j]：j++。

代码

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 int cmp(const void* a,const void* b){
    return (*(int*)a - *(int*)b);
 }
int* intersection(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
    qsort(nums1,nums1Size,sizeof(int),cmp);
    qsort(nums2,nums2Size,sizeof(int),cmp);
    int a = (nums1Size < nums2Size)?nums1Size:nums2Size;
    int* ans = (int*)malloc(sizeof(int)*a);
    *returnSize = 0;
    int i = 0,j = 0;
    int k = 0;
    while( i < nums1Size && j < nums2Size){
        if(nums1[i] < nums2[j]){
            i++;
        }
        else if(nums1[i] > nums2[j]){
            j++;
        }
        else{
            if(k == 0 || nums1[i] != ans[k-1]){
                ans[k++] = nums1[i];
            }
            i++;
            j++;
        }
    }
    *returnSize = k;
    return ans;
}

---

方法二：排序 + 二分查找

如果你不想同时移动两个指针，可以用二分查找。

核心逻辑：

1. 先对其中一个数组（比如 nums1）进行排序。
2. 遍历另一个数组 nums2 中的每个元素。
3. 在排序好的 nums1 中利用二分查找寻找该元素。
4. 找到后，同样要处理结果集的去重。
   代码

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int cmp(const void* a,const void* b){
    return (*(int*)a - *(int*)b);
}
bool binarySearch(int a[],int size,int target){
    int left = 0,right = size-1;
    while(left <= right){
        int mid = left+(right-left)/2;
        if(a[mid] == target){
            return true;
        }else if(a[mid] > target){
            right = mid-1;
        }else{
            left = mid+1;
        }
    }
    return false;
}
int* intersection(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
    qsort(nums1,nums1Size,sizeof(int),cmp);
    qsort(nums2,nums2Size,sizeof(int),cmp);
    int* ans = (int*)malloc(sizeof(int)*nums2Size);
    int k = 0;
    for(int i = 0;i < nums2Size;i++){
        if(i > 0 && nums2[i] == nums2[i-1]){
            continue;
        }
        if(binarySearch(nums1,nums1Size,nums2[i])){
            ans[k++] = nums2[i];
        }
    }
    *returnSize = k;
    return ans;
}

---

方法三：使用 uthash 库（模拟真正的 Set/Map）

在力扣的 C 语言环境下，是内置了 uthash.h 这个头文件的。你可以通过定义结构体来创建真正的哈希表。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
// #include "uthash.h"
struct HashTable{
    int key;
    UT_hash_handle hh;
};

int* intersection(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
    struct HashTable *set = NULL,*item,*tmp;
    int* res = (int*)malloc(sizeof(int)*nums1Size);
    int k = 0;

    for(int i = 0;i < nums1Size;i++){
        HASH_FIND_INT(set,&nums1[i],item);
        if(!item){
            item = malloc(sizeof(struct HashTable));
            item->key = nums1[i];
            HASH_ADD_INT(set,key,item);
        }
    }
    for(int i = 0;i < nums2Size;i++){
        HASH_FIND_INT(set,&nums2[i],item);
        if(item){
            res[k++] = nums2[i];
            HASH_DEL(set,item);
            free(item);
        }
    }
    HASH_ITER(hh,set,item,tmp){
        HASH_DEL(set,item);
        free(item);
    }
    *returnSize = k;
    return res;
}

下面我为你详细拆解这段代码的逻辑：

---

1. 核心结构体定义

struct HashTable {
    int key;            // 存储的值（在这里是数组里的数字）
    UT_hash_handle hh;  // 必须包含这个成员，它是 uthash 内部使用的隐式链表/哈希句柄
};

• UT_hash_handle hh ：这是 uthash 的核心。你不需要初始化它，但它是哈希表建立索引的关键。

---

2. 初始化与内存准备

struct HashTable *set = NULL, *item, *tmp;
int* res = (int*)malloc(sizeof(int) * nums1Size);
int k = 0;

• set = NULL ：在 uthash 中，一个指向结构体的 NULL 指针就代表一个空的哈希表。
• res ：申请结果数组的内存，最大长度不会超过 nums1Size。

---

3. 第一步：构建哈希表（去重存入）

for (int i = 0; i < nums1Size; i++) {
    HASH_FIND_INT(set, &nums1[i], item); // 在 set 中查找是否存在 nums1[i]
    if (!item) { // 如果没找到
        item = malloc(sizeof(struct HashTable));
        item->key = nums1[i];
        HASH_ADD_INT(set, key, item); // 将 item 加入哈希表，key 字段作为键
    }
}

• HASH_FIND_INT ：这是宏函数。它会检查 nums1[i] 是否已经在 set 里了。
• HASH_ADD_INT ：将新节点加入。通过这一步，nums1 中的所有元素都被存入了哈希表，且因为 if (!item) 的判断，自动完成了去重。

---

4. 第二步：寻找交集（并防止结果重复）

for (int i = 0; i < nums2Size; i++) {
    HASH_FIND_INT(set, &nums2[i], item); // 在 set 里找 nums2[i]
    if (item) { 
        res[k++] = nums2[i]; // 找到了，说明是交集
        HASH_DEL(set, item);  // 重要：从哈希表中删掉这个元素
        free(item);          // 释放内存
    }
}

• 核心技巧 ：为什么找到交集后要执行 HASH_DEL？
• 题目要求结果集中的元素必须是唯一的。
• 如果在 nums2 中有多个相同的数字（比如两个 2），第一次遇到 2 时，我们在哈希表里找到了它并存入结果；立即删掉它 后，第二次遇到 2 就找不到了，从而避免了结果数组 res 里出现重复的 2。

---

5. 第三步：善后工作（内存回收）

HASH_ITER(hh, set, item, tmp) {
    HASH_DEL(set, item);
    free(item);
}

• HASH_ITER：这是一个安全的遍历宏。
• 由于第二步只删除了交集部分，哈希表里可能还剩下一些只属于 nums1 的元素。为了防止内存泄漏 ，必须遍历并 free 掉剩余的节点。

---

总结：这段代码的精妙之处

1. 空间换时间：利用哈希表将查找交集的时间复杂度降到了平均 。
2. 原地去重 ：通过 HASH_DEL 巧妙地解决了结果集去重的问题，不需要再额外开辟一个 result_set。
3. 符合 C 语言工程规范：完整展示了"申请 -> 使用 -> 释放"的内存管理过程。

三种方法对比

方法	时间复杂度	空间复杂度	适用场景
排序 + 双指针	O ( n log ⁡ n ) O(n \log n) O(nlogn)	O ( 1 ) O(1) O(1)	内存限制极严，数组较大
二分查找	O ( n log ⁡ n ) O(n \log n) O(nlogn)	O ( 1 ) O(1) O(1)	其中一个数组极大，另一个极小
uthash (哈希表)	O ( n ) O(n) O(n)	O ( n ) O(n) O(n)	追求最优时间效率，允许额外空间

5、 350 两个数组的交集②

题目

代码

和上题差不多，用数组模拟哈希，不过多定义了一个变量用来记录交集元素的出现次数较小值

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* intersect(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize) {
    int cnt_1[1001] = {0};
    int cnt_2[1001] = {0};
    int* res = (int*)malloc(sizeof(int)*nums1Size);
    int k = 0;
    for(int i = 0;i < nums1Size;i++){
        cnt_1[nums1[i]]++;
    }
    for(int i = 0;i < nums2Size;i++){
        cnt_2[nums2[i]]++;
    }
    for(int i = 0;i < 1001;i++){
        if(cnt_1[i] != 0 && cnt_2[i] != 0){
            int a = (cnt_1[i] <= cnt_2[i])?cnt_1[i]:cnt_2[i];
            while(a > 0){
                res[k++] = i;
                a--;
            }
        }
    }
    *returnSize = k;
    return res;
}

时间复杂度：O(n)

空间复杂度：O(1)

6、202 快乐数

题目

代码

int get_sum(int n){
    int sum = 0;
    while(n != 0){
        sum += (n%10)*(n%10);
        n = n/10;
    }
    return sum;
}
bool isHappy(int n) {
    int sum = get_sum(n);
    int* ans = (int*)calloc(sizeof(int),820);
    while(sum != 1){
        if(ans[sum] == 1){
            return false;
        }
        else{
            ans[sum]++;
        }
        sum = get_sum(sum);
    }
    return true;
}

时间复杂度：O(logn)

空间复杂度：O(logn)

另解：快慢指针

int get_sum(int n){
    int sum = 0;
    while(n != 0){
        sum += (n%10)*(n%10);
        n = n/10;
    }
    return sum;
}
bool isHappy(int n) {
    // int fast = n;
    // int slow = n;
    // do{
    //     fast = get_sum(get_sum(fast));
    //     slow = get_sum(slow);
    // }while(fast != slow);
    int fast = get_sum(get_sum(n));
    int slow = get_sum(n);
    while(fast != slow){
        fast = get_sum(get_sum(fast));
        slow = get_sum(slow);
    }
    return fast==1;
}

时间复杂度：O(logn)

空间复杂度：O(1)

7、1 两数之和

题目

代码

暴力解，循环遍历i,j是否等于target

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
    *returnSize = 2;
    int* res = (int*)calloc(sizeof(int),2);
    int n = numsSize;
    // for(int i = 0;i < n-1;i++){
    //     for(int j = i+1;j < n;j++){
    //         if(nums[i]+nums[j]== target){
    //             res[0] = i;
    //             res[1] = j;
    //             break;
    //         }
    //     }
    // }
    // return res;
    for(int i = 0;i < n-1;i++){
        for(int j = i+1;j < n;j++){
            if(nums[i]+nums[j]== target){
                res[0] = i;
                res[1] = j;
                return res;
            }
        }
    }
    return NULL;
}

时间复杂度：O( n 2 n^2 n2)

空间复杂度：O(1)
另解 哈希表

代码

空间换时间

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
struct HashTable{
    int key;
    int value;
    UT_hash_handle hh;
};
int* twoSum(int* nums, int numsSize, int target, int* returnSize) {
    struct HashTable *set = NULL,*item,*tmp;
    for(int j = 0;;j++){
        int t = target - nums[j];
        HASH_FIND_INT(set,&t,item);
        if(item){
            int* res = (int*)malloc(sizeof(int)*2);
            *returnSize = 2;
            res[0] = item->value;
            res[1] = j;
            HASH_ITER(hh,set,item,tmp){
                HASH_DEL(set,item);
                free(item);
            }
            return res;
        }else{
            item = malloc(sizeof(struct HashTable));
            item->key = nums[j];
            item->value = j;
            HASH_ADD_INT(set,key,item);
        }
    }
}

时间复杂度：O( n n n)

空间复杂度：O(n)

8、454 四数相加

题目

代码

暴力解超出时间限制

用哈希表，先算nums1[i]+nums2[i]，存入哈希表，如果在哈希表中能找到则次数加一然后算nums3[i]+nums4[i]如果在哈希表中能找到则累加总次数。

struct HashTable{
    long long key;
    int count;
    UT_hash_handle hh;
};
int fourSumCount(int* nums1, int nums1Size, int* nums2, int nums2Size, int* nums3, int nums3Size, int* nums4, int nums4Size) {
    struct HashTable *set = NULL,*item,*tmp;
    long long Tatalcount = 0;
    long long sum = 0;
    for(int i = 0;i < nums1Size;i++){
        for(int j = 0;j < nums2Size;j++){
            sum = (long long)(nums1[i]+nums2[j]);
            HASH_FIND(hh,set,&sum,sizeof(long long),item);
            if(item){
                item->count++;
            }else{
                item = malloc(sizeof(struct HashTable));
                item->key = sum;
                item->count = 1;
                HASH_ADD(hh,set,key,sizeof(long long),item);
            }
        }
    }
    for(int i = 0;i < nums3Size;i++){
        for(int j = 0;j < nums4Size;j++){
            sum = -(long long)(nums3[i]+nums4[j]);
            HASH_FIND(hh,set,&sum,sizeof(long long),item);
            if(item){
                Tatalcount += item->count;
            }
        }
    }
    HASH_ITER(hh,set,item,tmp){
        HASH_DEL(set,item);
        free(item);
    }
    return Tatalcount;
}

时间复杂度：O( n 2 n^2 n2)

空间复杂度：O( n 2 n^2 n2)

Line 29: Char 28: runtime error: signed integer overflow: -1094795585 + -1094795585 cannot be represented in type 'int' [solution.c]报错了

这个报错非常经典，它揭示了 C 语言和 Python 在处理数字时的一个核心区别：数值溢出（Integer Overflow）。

在灵神的 Python 代码中，Python 会自动处理无限大的整数。但在 C 语言中，int 通常只有 32 位，最大只能表示约 21 亿（）。当你把两个很大的负数相加时，结果超出了 int 能承受的范围，系统就报错了。

1. 为什么会溢出？

报错信息中的 -1094795585 大约是 -11 亿。

两个 -11 亿相加等于 -22 亿 。

而在 C 语言中，32 位有符号整数（signed int）的范围是：

-22 亿 < -21.47 亿 ，所以它"漏"出去了，这就是 Signed Integer Overflow。

2. 如何修正？（最务实的两种方法）

方法 A：使用 long 或 long long（推荐）

将求和的变量类型改为 long（在 64 位系统下通常是 64 位）或 long long，它们可以表示极大的数值。

• 修改结构体 ：把 key 的类型改掉。
• 修改求和变量：确保计算过程不溢出。

struct HashTable {
    long long key;  // 改为 long long，足以容纳所有 int 相加的结果
    int count;
    UT_hash_handle hh;
};

// 在查找和计算时：
long long sum = (long long)nums1[i] + nums2[j]; 
// 查找逻辑
HASH_FIND(hh, map, &sum, sizeof(long long), item); 

注意：因为 key 不再是 int，我们需要用通用的 HASH_FIND 和 HASH_ADD 宏。

方法 B：针对 uthash 的特化修正

如果你想继续用 int，必须先判断两个数相加是否会溢出。但在算法题中，通常最简单粗暴且有效的方法就是提升变量等级。

---

💡 核心知识点补充

• HASH_FIND_INT ：是 uthash 专门为 int 优化的简写宏。
• HASH_FIND ：是通用宏。当你把 key 类型换成 long long、double 甚至 struct 时，必须用它，并明确告知 sizeof(key_type)。

这就是 C 语言的"迷人"之处------你必须像管账先生一样精准地控制每一块内存和每一个数字的大小。这虽然麻烦，但也是为什么 C 语言比 Python 快几十倍的原因。

杂记 如何在本地测试代码