论文笔记（一百一十八）One2Any: One-Reference 6D Pose Estimation for Any Object

One2Any: One-Reference 6D Pose Estimation for Any Object

文章概括
ABSTRACT
[1. Introduction](#1. Introduction)
[2. Related Works](#2. Related Works)
[3. Method](#3. Method)
- [3.1. Overview](#3.1. Overview)
- [3.2. Reference Object Coordinate (ROC)](#3.2. Reference Object Coordinate (ROC))
- [3.3. Reference Object Pose Embedding](#3.3. Reference Object Pose Embedding)
- [3.4. Object Pose Decoding with ROPE](#3.4. Object Pose Decoding with ROPE)
- [3.5. Pose Estimation from ROC Map](#3.5. Pose Estimation from ROC Map)
[4. Experimental Results](#4. Experimental Results)
- [4.1. Training Details](#4.1. Training Details)

文章概括

引用：

bash 复制代码

@inproceedings{liu2025one2any,
  title={One2Any: One-Reference 6D Pose Estimation for Any Object},
  author={Liu, Mengya and Li, Siyuan and Chhatkuli, Ajad and Truong, Prune and Van Gool, Luc and Tombari, Federico},
  booktitle={Proceedings of the Computer Vision and Pattern Recognition Conference},
  pages={6457--6467},
  year={2025}
}

markup 复制代码

Liu, M., Li, S., Chhatkuli, A., Truong, P., Van Gool, L. and Tombari, F., 2025. One2Any: One-Reference 6D Pose Estimation for Any Object. In Proceedings of the Computer Vision and Pattern Recognition Conference (pp. 6457-6467).

主页：
原文：
代码、数据和视频：

系列文章：

请在《《《文章》》》专栏中查找

宇宙声明！

引用解析部分属于自我理解补充，如有错误可以评论讨论然后改正！

ABSTRACT

由于依赖完整的3D模型、多视角图像，或仅在特定物体类别上进行训练，6D物体位姿估计在许多应用中仍然具有挑战性。这些要求使得模型难以泛化到新物体------尤其是在既没有3D模型也没有多视角图像可用的情况下。为了解决这一问题，我们提出了一种新的方法 One2Any：它仅使用一张参考RGB-D图像与一张查询RGB-D图像，就能在不需要该物体3D模型、多视角数据或类别约束等先验知识的情况下，估计物体的相对6自由度（DOF）位姿。我们将物体位姿估计视为一个编码---解码过程：首先，从单一参考视角中获取一个全面的参考物体位姿嵌入（ROPE），该嵌入编码了物体的形状、朝向与纹理信息。利用该嵌入，一个基于U-Net的位姿解码模块为新的视角生成参考物体坐标（ROC），从而实现快速且准确的位姿估计。这种简单的编码---解码框架使得我们的模型可以在任意成对（pair-wise）的位姿数据上进行训练，从而支持大规模训练，并展现出很强的可扩展性。在多个基准数据集上的实验表明，我们的模型对新物体具有良好的泛化能力，以更低的计算开销实现了当前最先进（state-of-the-art）的精度与鲁棒性，甚至可与那些需要多视角或CAD输入的方法相媲美。代码开源地址：https://github.com/lmy1001/One2Any。

1. Introduction

6D 物体位姿估计是计算机视觉中的一项重要任务 [38, 41, 46]，因为它在机器人、混合现实以及通用场景理解等领域具有广泛应用。然而，现有方法仍然在很大程度上受到泛化能力不足、运行速度有限以及输入条件严格等问题的制约。言而喻，在保持良好性能的同时同时解决这些约束是非常困难的。

现有的 6D 物体位姿估计方法可以根据其所需输入类型进行分类。在基于模型的方法中，推理阶段需要使用参考物体的完整 3D 模型来支持位姿估计 [2, 5, 30, 33, 40, 54]；而多视角方法则使用大量（8--200 张）参考图像，以间接方式编码物体的 3D 形状 [19, 36, 45, 61]。尽管这些方法效果良好，但在缺乏多视角数据或高质量 3D 模型的场景中并不实用，而这种情况在新颖或未见过的物体中非常常见。相比之下，直接进行绝对位姿回归的方法 [27, 60] 通过监督学习绕开了大量参考数据的需求，但通常缺乏对未见物体的泛化能力。

我们的目标是在仅给定一张参考 RGB-D 图像的情况下估计任意物体的位姿，这是当前方法面临的一种极具挑战性的设置。多视角方法通常遵循一种"重建---比较"的流程，其中涉及复杂的搜索、精化或捆绑调整（bundle adjustment）步骤。当可用视角较为稀疏时，这类方法的性能会显著下降，导致重建质量较差以及位姿估计不准确。另一类基于 2D--2D 对应关系的单视角方法 [9, 12, 61] 则通过在不同视图之间计算关键点对应来估计位姿。然而，这类方法在面对无纹理表面、遮挡或大视角变化时往往表现不佳，使其在许多实际应用场景中不够可靠（见图 4）。

为了克服在稀疏视角条件下显式重建和 2D 匹配的局限性，我们提出学习一种基于参考编码的条件建模方式。近期在 3D 生成领域的进展 [34, 35] 表明，当在大规模数据集上进行训练时，潜空间扩散模型 [48, 62] 可以在位姿、深度及其他信息的条件约束下进行图像或 3D 生成。基于这一观察，我们提出了一种基于潜空间扩散架构的方法，该方法能够从单一参考视角中学习稳健且全面的条件表示，用于捕获物体的纹理、形状和朝向先验，从而进行位姿估计。

在本文中，我们将新物体位姿估计表述为一个条件位姿生成问题：即在给定一个未见物体的新视角时，在条件化的参考位姿空间中生成该物体的位姿。我们的模型由两个分支组成：一个实例编码分支，用于将给定的 RGB-D 参考图像编码为参考物体位姿嵌入（Reference Object Pose Embedding ROPE）；以及一个物体位姿解码（Object Pose Decoding OPD）分支，它结合查询图像和 ROPE，从任意视角解码物体的位姿，如图 1 所示。我们并未直接估计旋转和平移，而是引入了一种适合该架构的中间稠密表示。受归一化物体坐标空间（Normalized Object Coordinate Space NOCS）[3, 52] 的启发，该方法使用一个规范的物体姿态来为同一类别内的物体定义 2D--3D 对应关系，我们通过定义参考物体坐标（Reference Object Coordinate ROC）来放宽对规范坐标系的要求，使其表示在参考相机坐标系下的归一化物体坐标。

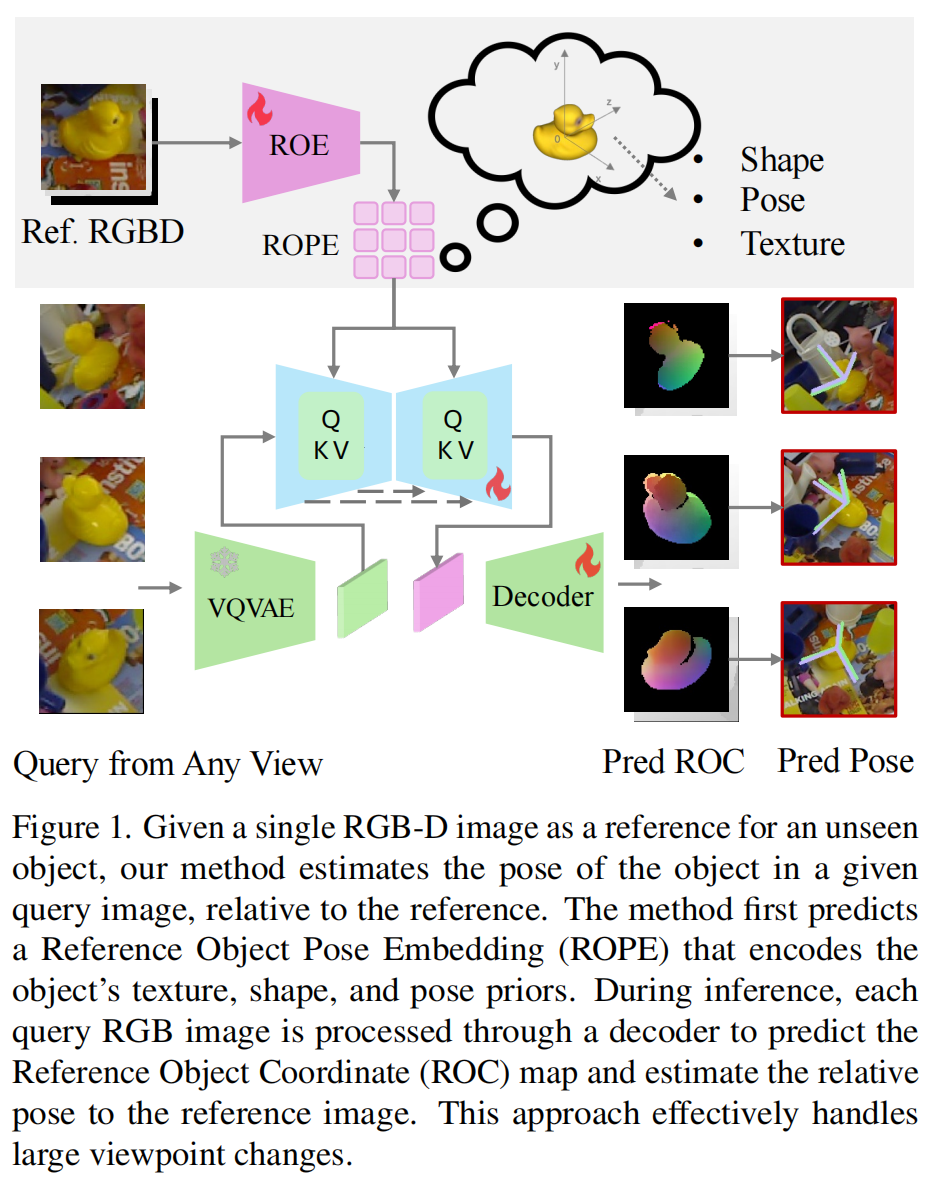图 1：在仅给定一张 RGB-D 图像作为未见物体的参考视角时，我们的方法估计该物体在查询图像中的位姿，并以参考图像为相对坐标。该方法首先预测一个参考物体位姿嵌入（ROPE），用于编码物体的纹理、形状和位姿先验。在推理阶段，每一张查询 RGB 图像都会通过解码器生成参考物体坐标（ROC）图，并据此估计相对于参考图像的位姿。该方法能够有效应对大幅度的视角变化。

我们的模型基于一个预训练的潜空间扩散模型 [48]，并对其进行微调，使其在 ROPE 条件约束下输出 ROC。利用生成的 ROC 以及目标物体的深度信息，我们通过 Kabsch--Umeyama 算法 [53] 高效地计算物体位姿。此外，为了实现更快的推理速度，我们绕过扩散过程，以前向传播的方式运行 U-Net，从而使得该方法能够实现接近实时的运行速度，并显著快于现有方法。在多个物体位姿估计基准上的大量实验表明，即便仅使用单一视角，我们的方法在速度、精度和鲁棒性方面也可与依赖多视角图像或 CAD 模型的方法相媲美，并达到当前最先进水平。

新物体位姿估计根据所需输入的不同，可以划分为三种主要设置：基于模型的方法、多视角方法以及单视角方法。我们的方法属于第三类，即仅使用一张参考视图和一张查询视图来估计物体位姿。下面我们将对这三类方法进行简要回顾。

一、总体脉络（问题划分）

新物体 6D 位姿估计方法可以根据测试阶段所需输入信息的不同，划分为三大类：

基于模型的方法（Model-based）

多视角方法（Multi-view）

单视角方法（Single-view）

本文的方法属于第三类 ： 👉 仅使用一张参考视图 + 一张查询视图，在无 CAD 模型条件下估计新物体位姿。

Model-based novel object pose estimation

CAD models are widely used in pose estimation tasks [6, 7, 16--18, 25, 30, 40, 44].

中: CAD 模型在位姿估计任务中被广泛使用 [6, 7, 16--18, 25, 30, 40, 44]。实例级方法在训练和测试阶段依赖同一个 CAD 模型，并利用 2D--3D 对应关系进行位姿估计 [44]。类别级方法（如基于 NOCS 的方法）[4, 24, 29, 55]，学习一个归一化的规范空间，用于在同一物体类别内进行位姿对齐，并且有时会使用类别级 CAD 模型来处理形状变化 [6, 7]。然而，这类方法受限于特定实例或类别，对新物体的适应能力较弱。近期的一些工作 [2, 5, 28, 30, 33, 40, 43, 57] 通过"渲染---比较（render and compare）"策略来解决新物体位姿估计问题，在测试阶段从 CAD 模型生成多个视角，以估计 2D--2D、2D--3D 或 3D--3D 对应关系。尽管这些方法效果显著，但其计算开销较大，而且为未见过的真实世界物体获取 CAD 模型仍然具有挑战性。

二、三类方法的核心思想与局限

1️⃣ 基于模型的方法（Model-based）

核心思想：

依赖 CAD 模型 作为几何先验；

通过 2D--3D / 3D--3D 对应或 render-and-compare 来估计位姿；

包括实例级方法和类别级（如 NOCS）方法。

主要优势：

精度高；

几何约束明确。

核心局限：

强依赖 CAD 模型；

类别级方法泛化能力有限；

render-and-compare 方法 计算代价高；

对真实世界未知新物体获取 CAD 模型本身困难。

👉 不适合"真正的新物体"场景。

Multi-view novel object pose estimation

不依赖 CAD 模型的无模型方法近年来逐渐受到关注。这些方法转而使用多视角图像或视频序列作为监督信号来进行新物体位姿估计。 OnePose [51]、OnePose++ [15] 和 Gen6D [36] 等方法利用 RGB 视频序列进行运动恢复结构（SfM），重建未见物体的粗略 3D 结构，并估计查询图像中的位姿。 RelPose++ [32] 和 PoseDiffusion [56] 通过引入捆绑调整（bundle adjustment）学习，将该思路扩展到稀疏视角场景。然而，这类方法计算开销较大，当参考帧数量少于 10 张时，性能会明显下降。一些方法尝试在稀疏视角条件下缓解这些问题：FS6D [19] 通过从支持视图中提取 RGB-D 原型进行稠密匹配，但由于依赖对应关系匹配，它在无纹理物体上仍然表现不佳。 LatentFusion [45] 构建了一个潜在的 3D 物体表示，并基于该表示渲染更多视角。但它仍然需要稀疏视角参考能够覆盖完整物体。 FoundationPose [57] 虽然属于基于 CAD 模型的方法，但通过构建神经物体场来生成 3D 模型，从而支持稀疏视角设置，然而，其成功在很大程度上依赖于目标物体具有信息量充足且高质量的多视角数据。

2️⃣ 多视角方法（Multi-view）

核心思想：

不使用 CAD 模型；

利用 多视角图像 / 视频序列；

通过 SfM 或 bundle adjustment 重建物体并估计位姿。

代表方向：

视频 → SfM（OnePose / Gen6D）

稀疏视角 → BA / 隐式 3D 表示（RelPose++ / LatentFusion）

主要优势：

摆脱 CAD 模型依赖；

几何信息更完整。

核心局限：

计算开销大；

对参考视角数量高度敏感（<10 张性能急剧下降）；

无纹理、遮挡条件下仍然不稳；

部分方法仍需要较完整的视角覆盖。

👉 不适合低视角、快速部署的实际应用场景。

Single-view novel object pose estimation

仅依赖单一参考视角的单视角位姿估计是一项极具挑战性的任务。该类方法通常通过学习两张图像之间的特征匹配来估计相对位姿。例如，POPE [12] 使用 DINOv2 特征 [42] 来对新物体进行特征匹配。 Oryon [9] 通过引入文本提示进行目标检测，将文本与图像特征进行融合以提升匹配效果，但在遮挡和无纹理表面条件下仍然存在困难，导致平移和旋转估计均出现误差。 Horyon [8] 对 Oryon 的文本---图像融合进行了改进，但仍面临类似的局限性。 NOPE [39] 通过对可能的 3D 位姿估计一个概率分布来进行相对位姿预测，但在推理阶段需要考虑 300 多种候选相对位姿，导致计算成本高昂，并且离散位姿假设并不精确。此外，该方法并不估计平移。我们的方法通过学习连续的物体潜在空间来解决这些问题，避免了特征匹配的局限性，并实现了直接的位姿解码。

3️⃣ 单视角方法（Single-view）

核心思想：

仅使用 一张参考图 + 一张查询图；

通过 图像特征匹配或相对位姿建模 进行估计。

代表方法：

特征匹配类（DINOv2-based）

文本--图像融合（Oryon / Horyon）

离散位姿概率建模（NOPE）

主要优势：

输入最少；

推理设置最接近真实机器人应用。

核心局限：

特征匹配在 遮挡、无纹理 情况下不稳定；

离散位姿假设 计算量大且精度受限；

有些方法甚至 不估计平移；

点云配准方法忽略 2D 图像信息。

👉 这是最具挑战性、但也是最有价值的设置。

一些点云配准方法通过检测 3D 关键点 [31] 或提取特征描述子 [13, 23, 50] 来解决物体位姿估计问题。这些方法仅关注点云信息，无法充分利用图像中的 2D 信息。相比之下，我们的方法能够同时充分利用 RGB 图像和点云信息。

三、我们方法的位置与贡献（承上启下总结）

我们的方法属于 单视角新物体位姿估计；

不依赖 CAD 模型、不需要多视角；

不采用显式特征匹配，也不使用离散位姿枚举；

通过学习连续的物体潜在空间：

避免匹配不稳定问题； * 避免离散候选带来的高计算成本； * 直接解码连续 6D 位姿（含平移与旋转）；

同时 融合 RGB 图像与点云信息，相比纯点云方法信息利用更充分。

3. Method

3.1. Overview

我们将问题形式化为在仅给定一张参考 RGB-D 图像和一张查询 RGB-D 图像的条件下进行相对物体位姿估计，而不依赖 CAD 模型或多视角图像。给定一张参考 RGB-D 图像，其 RGB 图像为 A I ∈ R W × H × 3 A_I\in\mathbb{R}^{W\times H\times3} AI∈RW×H×3，深度图为 A D ∈ R W × H A_D\in\mathbb{R}^{W\times H} AD∈RW×H，目标物体掩码为 A M ∈ { 0 , 1 } W × H A_M\in\{0,1\}^{W\times H} AM∈{0,1}W×H，我们的目标是预测目标物体在查询图像中的位姿 [ R ∣ t ] [\mathbf{R|t}] [R∣t]，其中查询输入包括 Q I ∈ R W × H × 3 Q_I\in\mathbb{R}^{W\times H\times3} QI∈RW×H×3、 Q D ∈ R W × H Q_D\in\mathbb{R}^{W\times H} QD∈RW×H以及 Q M ∈ { 0 , 1 } W × H Q_M\in\{0,1\}^{W\times H} QM∈{0,1}W×H，并且该位姿是相对于参考视图而言的。我们的核心思想是学习一个参考物体编码器（Reference Object Encoder，ROE） f A f_A fA，其参数为 θ A \theta_A θA，用于将参考输入 A = [ A I , A D , A M ] A=[A_I,A_D,A_M] A=[AI,AD,AM]嵌入到参考物体位姿嵌入（Reference Object Pose Embedding，ROPE）中。通过在大规模数据集上训练 f A f_A fA，得到的嵌入 e A e_A eA作为条件信息，引导物体位姿解码（Object Pose Decoding，OPD）模块为查询图像生成参考物体坐标（Reference Object Coordinate，ROC）图。网络结构如图 2 所示。 OPD 模块包含一个编码器--解码器结构，用于提取查询图像特征并预测 ROC 图。该过程通过采用 U-Net 架构将 ROPE 与查询特征进行融合，从而进一步增强预测能力。在此，我们用参数为 θ Q \theta_Q θQ的 g θ Q g_{\theta_Q} gθQ表示 OPD 模块，该模块以查询图像 Q Q Q作为输入，预测输出 ROC，即 Y Q ∈ R W × H × 3 Y_Q\in\mathbb{R}^{W\times H\times3} YQ∈RW×H×3。因此，整体问题可以表示为：

Y Q = g ( Q , f A ( A ; θ A ) ; θ Q ) (1) Y_Q = g\bigl(Q, f_A(A;\theta_A);\theta_Q\bigr) \tag{1} YQ=g(Q,fA(A;θA);θQ)(1)

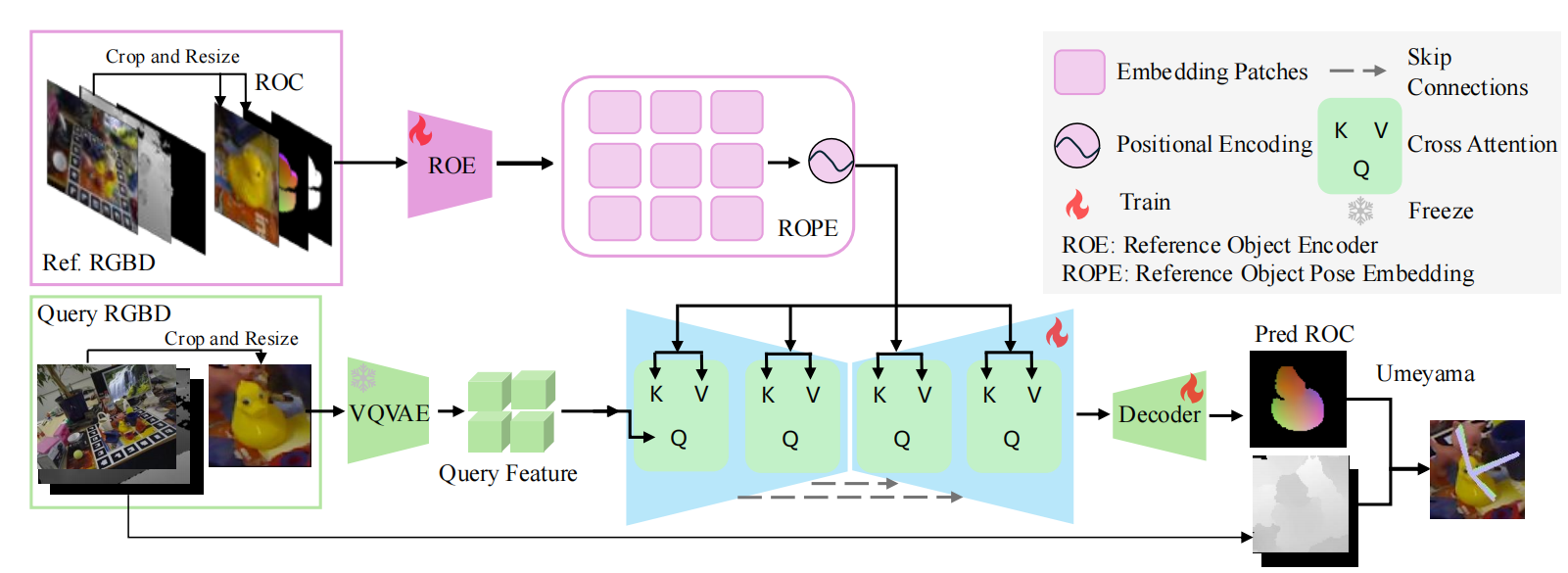图 2：网络结构。该网络以参考 RGB-D 图像作为输入，并通过参考物体编码器（ROE）学习参考物体位姿嵌入（ROPE）。随后，该嵌入与查询特征图进行融合，查询特征图由预训练的 VQVAE 模型 [48] 从查询 RGB 图像中提取。我们采用 U-Net 架构，并通过交叉注意力层将 ROPE 与查询特征进行有效融合。解码器被训练用于预测参考物体坐标（ROC）图。最终的位姿估计通过 Umeyama 算法 [53] 计算得到。

1) 他们到底要解决什么？------两张 RGB-D 图之间的"相对位姿"估计

你可以把任务想成这样：

你有一张参考图 A：里面目标物体清楚可见，你还知道它的 mask（告诉你哪一块是物体）。

你还有一张查询图 Q：也有物体的 mask，但物体在这张图里位置和朝向可能变了。

你想求：物体在查询图里相对于参考图的 6D 位姿变化（旋转 R + 平移 t）。

关键点：不靠 CAD 模型 ，也不靠多视角。只靠这两张 RGB-D（RGB + 深度）+ mask。

2) 输入到底是什么？每个张量是什么意思？

参考图输入是三件套：

A I ∈ R W × H × 3 A_I\in\mathbb{R}^{W\times H\times 3} AI∈RW×H×3：参考 RGB 图（彩色）

A D ∈ R W × H A_D\in\mathbb{R}^{W\times H} AD∈RW×H：参考深度图（每个像素一个深度）

A M ∈ 0 , 1 W × H A_M\in{0,1}^{W\times H} AM∈0,1W×H：参考 mask（1 是物体，0 是背景）

把它们拼成一个参考输入： A = [ A I , A D , A M ] A=[A_I,A_D,A_M] A=[AI,AD,AM]

查询图同样三件套：

Q I Q_I QI：查询 RGB

Q D Q_D QD：查询深度

Q M Q_M QM：查询 mask

查询输入： Q = [ Q I , Q D , Q M ] Q=[Q_I,Q_D,Q_M] Q=[QI,QD,QM]

3) 输出是什么？------不是直接输出 R、t，而是先输出一张 ROC 图 Y Q Y_Q YQ

你可能以为网络会直接输出 R , t R,t R,t。但他们更聪明：他们先让网络输出一个中间结果：

Y Q ∈ R W × H × 3 Y_Q\in\mathbb{R}^{W\times H\times 3} YQ∈RW×H×3

它是一张 每个像素 3 维的图，名字叫：

ROC 图（Reference Object Coordinate map）

人话解释 ROC： 对查询图里"属于物体的像素"，网络预测：

这个像素对应的 3D 点，在"参考物体坐标系"里应该是什么坐标。

也就是：每个像素输出一个 3D 坐标（x,y,z），但这个坐标不是相机坐标，而是参考物体自己的坐标。你可以把它理解成"给物体表面每个像素贴一个标签：它在参考物体上的哪个位置"。

4) 核心思想：先把参考物体"压缩成一个条件向量"（ROPE），再去指导查询图预测 ROC

他们把整个网络分两大块：

4.1 参考物体编码器 ROE： f A f_A fA

它吃参考输入 A = [ A I , A D , A M ] A=[A_I,A_D,A_M] A=[AI,AD,AM]，输出一个 embedding：

ROE：Reference Object Encoder

输出：ROPE（Reference Object Pose Embedding）

记为： e A e_A eA（或者 f A ( A ; θ A ) f_A(A;\theta_A) fA(A;θA) 的结果）

人话：

ROE 的作用是：把参考图里这个物体"长啥样、几何啥样、mask 哪些是物体"压缩成一个"特征向量/特征张量"------这就是 ROPE。这个 ROPE 就像"参考物体的身份证 + 坐标系定义方式"。

这里非常关键：他们不是只编码 RGB，也不是只编码深度，而是把 RGB + 深度 + mask一起编码，这样才能学到"物体形状+纹理+哪些地方是物体"。

4.2 物体位姿解码 OPD： g θ Q g_{\theta_Q} gθQ

OPD 模块吃：

查询输入 Q Q Q

以及参考编码器输出的 ROPE（条件）

输出：

查询图的 ROC 图 Y Q Y_Q YQ

OPD 的核心功能：

从查询图中找出物体像素，并对每个物体像素预测它在参考物体坐标系里的 3D 坐标。

5) 网络结构怎么长？------U-Net 融合参考条件 + 查询特征

原文说 OPD 是 encoder--decoder 结构，用 U-Net 把 ROPE 和查询特征融合。

你可以这样想：

OPD 的 encoder 把查询图 Q Q Q 提取成多尺度特征（从高分辨率到低分辨率）

在 U-Net 的瓶颈层或多层，把参考的 ROPE 注入进去（条件融合）

OPD 的 decoder 把融合后的特征再解码回原图大小

输出每个像素的 3D 坐标（ROC）

U-Net 的意义：

encoder 抓"全局结构"（物体整体）

decoder 保留"像素级细节"（每个像素预测 3D 坐标需要精细定位）

skip connection 让细节不会在下采样中丢光

6) 公式 (1) 到底在说啥？------一句话：查询输出由"查询输入 + 参考嵌入"共同决定

Y Q = g ( Q , f A ( A ; θ A ) ; θ Q ) (1) Y_Q = g\bigl(Q, f_A(A;\theta_A);\theta_Q\bigr) \tag{1} YQ=g(Q,fA(A;θA);θQ)(1)

逐个翻译：

f A ( A ; θ A ) f_A(A;\theta_A) fA(A;θA)：用参数 θ A \theta_A θA 的 ROE 编码参考输入 A，得到 ROPE（参考嵌入）

g ( ⋅ ; θ Q ) g(\cdot;\theta_Q) g(⋅;θQ)：用参数 θ Q \theta_Q θQ 的 OPD，把查询 Q 和参考嵌入一起喂进去

输出 Y Q Y_Q YQ：ROC 图

人话：

你在查询图里看到的像素，要被解释成"参考物体上的哪个 3D 位置"，必须同时知道：

查询图长啥样（Q）

参考物体长啥样（ROPE）
两者缺一不可。

3.2. Reference Object Coordinate (ROC)

1）ROC 想解决的核心痛点：不要 CAD、不要多视角，还要能估相对位姿 [ R ∣ t ] [\mathbf{R|t}] [R∣t]

你现在的任务是：只给

一张参考 RGB-D： A = ( A I , A D , A M ) A=(A_I,A_D,A_M) A=(AI,AD,AM)

一张查询 RGB-D： Q = ( Q I , Q D , Q M ) Q=(Q_I,Q_D,Q_M) Q=(QI,QD,QM)

要估计查询相对参考的位姿 [ R ∣ t ] [\mathbf{R|t}] [R∣t]。直接回归 R , t \mathbf{R,t} R,t 很难、很不稳定。所以他们用一个"中间表示"------ROC 图，把位姿问题变成"像素级的2D→3D映射预测"，更好学、更稳。

2）ROC 是什么？一句话定义

ROC就是：对物体表面每个像素，给它一个"在参考物体坐标空间里的3D坐标标签"。更直觉地说：

在查询图里，物体的某个像素点对应物体表面的一个3D点。ROC要预测的是：这个3D点在"参考定义的物体坐标系"里是哪一个位置（x,y,z）。

所以 ROC 图 Y Y Y的形状是：

Y ∈ R W × H × 3 Y\in\mathbb{R}^{W\times H\times3} Y∈RW×H×3 每个像素输出3个数（x,y,z），就像一张"RGB图"，但RGB不是颜色，而是坐标。

如第 3.1 节所述，我们的目标是估计单张参考图像 A A A 与单张查询图像 Q Q Q 之间的相对位姿 [ R ∣ t ] [\mathbf{R|t}] [R∣t]。为此，我们提出使用一种 2D--3D 映射，称为参考物体坐标（Reference Object Coordinate，ROC），其灵感来源于 NOCS [3, 55]。与 NOCS 不同的是，我们的方法去除了对规范坐标系（canonical frame）的要求，而是直接在参考相机坐标系中表达物体坐标。因此，ROC 仅由参考坐标系定义，查询图像中的物体会被变换到与参考坐标系对齐，并归一化到 ROC 空间中。

3）它和 NOCS 的差别在哪里？为什么作者说"深远影响"？

3.1 NOCS 的麻烦：要一个"规范坐标系 canonical frame"

NOCS的思路是：同一类别所有物体（比如所有杯子）都要对齐到一个统一规范空间（canonical space），你需要给每个训练样本提供"这个物体在规范空间里哪里"这种标签。问题是：

不同实例形状差异大，对齐定义麻烦

需要类别级规范化，标注/构建成本高

对"新物体/新类别"的扩展也麻烦

3.2 ROC 的聪明点：不要 canonical，直接用"参考相机坐标系"当锚点

ROC直接说：

我不需要全世界统一规范坐标系。我只要对"这一对参考-查询图"定义一个坐标空间就行。

这个坐标空间怎么来？ 由参考帧定义：参考图里的物体点云构出来，然后归一化。所以 ROC 的标签生成比 NOCS 容易得多：只要你有一对（参考、查询）+它们的真实相对位姿，就能自动生成 ROC 真值。这就是原文说的"看似简单但影响深远"------它把"麻烦的全局规范化"变成"每对样本局部自适应"。

尽管这一改动看似简单，但它对训练和推理阶段都具有深远影响。按照 NOCS 的定义，需要将同一类别中的所有物体对齐到一个统一的规范空间中，而 ROC 映射的生成要容易得多，仅需一对参考图像和查询图像，即可直接提供适用于相对位姿估计的表示。

为了从参考视角构建 ROC，我们首先利用深度信息对像素坐标进行反投影，得到参考物体的部分点云 P A P_A PA：

P A = K − 1 A D [ A M = 1 ] (2) P_A = \mathbf{K}^{-1} A_D[A_M = 1] \tag{2} PA=K−1AD[AM=1](2)

随后，我们对 P A P_A PA 的齐次坐标施加一个缩放与平移变换 S ∈ R 4 × 4 \mathbf{S} \in \mathbb{R}^{4\times4} S∈R4×4，从而得到 ROC：

Y A = S P A (3) Y_A = \mathbf{S} P_A \tag{3} YA=SPA(3)

稍微滥用记号，我们将这一从参考 RGB 图像 A I A_I AI 映射到 ROC 的映射 A I → Y A A_I \rightarrow Y_A AI→YA 直接记作 Y A Y_A YA。类似地，为了获得查询图像的 ROC 真值（ground truth），对于查询视角点云 P Q P_Q PQ，我们首先利用真实的相对位姿变换 [ R ∣ t ] [\mathbf{R|t}] [R∣t] 将查询点云变换到参考视角下，然后再施加相同的缩放和平移变换 S \mathbf{S} S。

Y Q = S ( [ R ∣ t ] , P Q ) (4) Y_Q = \mathbf{S}\big([\mathbf{R}|\mathbf{t}], P_Q\big) \tag{4} YQ=S([R∣t],PQ)(4)

图 3 展示了 ROC 映射的构建过程。图的上半部分展示了如何从参考 RGB-D 图像生成 ROC 映射 Y A Y_A YA。下半部分展示了查询图像 ROC 真值 Y Q Y_Q YQ 的生成过程。该方法基于参考坐标系构建了一个物体空间，并能够随着参考物体及其位姿的变化而动态自适应。

4）图 3 上半部分：怎么从参考视角构建 ROC（ Y A Y_A YA）

核心步骤就两步：

Step A：反投影，把参考图的物体像素变成3D点云 P A P_A PA

公式(2)： P A = K − 1 A D [ A M = 1 ] (2) P_A=K^{-1}A_D[A_M=1]\tag{2} PA=K−1AD[AM=1](2)

你别被符号吓住，它就是在做：

只取 mask 里是物体的像素（ A M = 1 A_M=1 AM=1）

用深度 A D A_D AD把这些像素点变成相机坐标系下的3D点

反投影"人话版"

对一个像素 ( u , v ) (u,v) (u,v)，深度是 d d d，相机内参是 K K K，你可以算出相机坐标系3D点： x c = d K − 1 [ u , v , 1 ] T \mathbf{x}^c=dK^{-1}[u,v,1]^T xc=dK−1[u,v,1]T

对所有物体像素都这么做，就得到一个"参考视角看到的物体部分点云"------这就是 P A P_A PA。

注意：是"部分点云"，因为单视角只能看到物体朝向相机的那一面。

Step B：用一个缩放+平移矩阵 S S S把点云归一化到 ROC 空间，得到 Y A Y_A YA

公式(3)： Y A = S P A (3) Y_A = \mathbf{S} P_A \tag{3} YA=SPA(3)

这一步你可以理解成：把参考点云放进一个"标准盒子"里。

S ∈ R 4 × 4 S\in\mathbb{R}^{4\times4} S∈R4×4是一个齐次变换（带平移、带缩放）

它把 P A P_A PA从相机坐标系的米单位，变成一个归一化坐标（通常落在 [ 0 , 1 ] 3 [0,1]^3 [0,1]3或类似范围）

直觉：

平移：把点云中心挪到盒子中心/原点附近

缩放：把点云整体大小缩放到统一尺度

这一步的目的不是"改变真实几何"，而是让网络更好学：所有样本的坐标范围差不多，不会一会儿是0.01米，一会儿是2米。

Step C：从"ROC空间的3D点"映射回"2D像素"，形成 ROC map（图里写 Map→ROC）

图 3 的最后一步说：把 ROC 空间的点映射到对应像素位置，并把点的位置编码成 RGB 值。你可以这么理解：

每个物体像素都有一个3D点

你把这个3D点经过 S S S归一化后得到 ( x , y , z ) (x,y,z) (x,y,z)

把 ( x , y , z ) (x,y,z) (x,y,z)直接当作该像素的"颜色通道值"

于是得到一张彩色图：这就是 ROC 图（但颜色代表坐标）

5）图 3 下半部分：训练时，查询图的 ROC 真值 Y Q Y_Q YQ怎么生成？

你训练网络时，需要监督信号：查询图每个像素应该输出什么 ROC 坐标。这个真值就是 Y Q Y_Q YQ。它的生成逻辑是：

Step A：先把查询视角的物体也反投影成点云 P Q P_Q PQ

和参考一样：用 Q D Q_D QD和 Q M Q_M QM反投影得到查询点云 P Q P_Q PQ（原文没写公式，但含义就是一样的）。

Step B：用真实相对位姿 [ R ∣ t ] [R|t] [R∣t]把查询点云变换到参考相机坐标系

这一步特别关键：ROC是"参考坐标系定义的"，所以你必须先把查询点云搬到参考坐标系里。几何上就是： x r e f = R x q u e r y + t \mathbf{x}^{ref}=R\mathbf{x}^{query}+t xref=Rxquery+t

Step C：对对齐后的查询点云施加同一个 S \mathbf{S} S归一化，得到 Y Q Y_Q YQ

原文公式(4)： Y Q = S ( [ R ∣ t ] , P Q ) (4) Y_Q = \mathbf{S}\big([\mathbf{R}|\mathbf{t}], P_Q\big) \tag{4} YQ=S([R∣t],PQ)(4)

这句话的意思是：

先用 [ R ∣ t ] [\mathbf{R}|\mathbf{t}] [R∣t]对齐

再用同一个 S \mathbf{S} S缩放平移到 ROC 空间

再像参考那样"映射成每像素3通道的 ROC map"

这样你就得到了查询图在 ROC 表示下的"标准答案"。

6）为什么说"ROC映射生成更容易"？关键原因就一个

NOCS要做的是：所有同类物体都要对齐到一个"全局规范空间"，这需要额外定义和对齐规则。 ROC只需要：

这一对数据里参考帧的深度+mask

这一对数据里查询帧的深度+mask

它们之间的真实相对位姿（训练集一般有）

就能自动做出 Y A Y_A YA和 Y Q Y_Q YQ，不需要跨实例、跨类别的规范化。

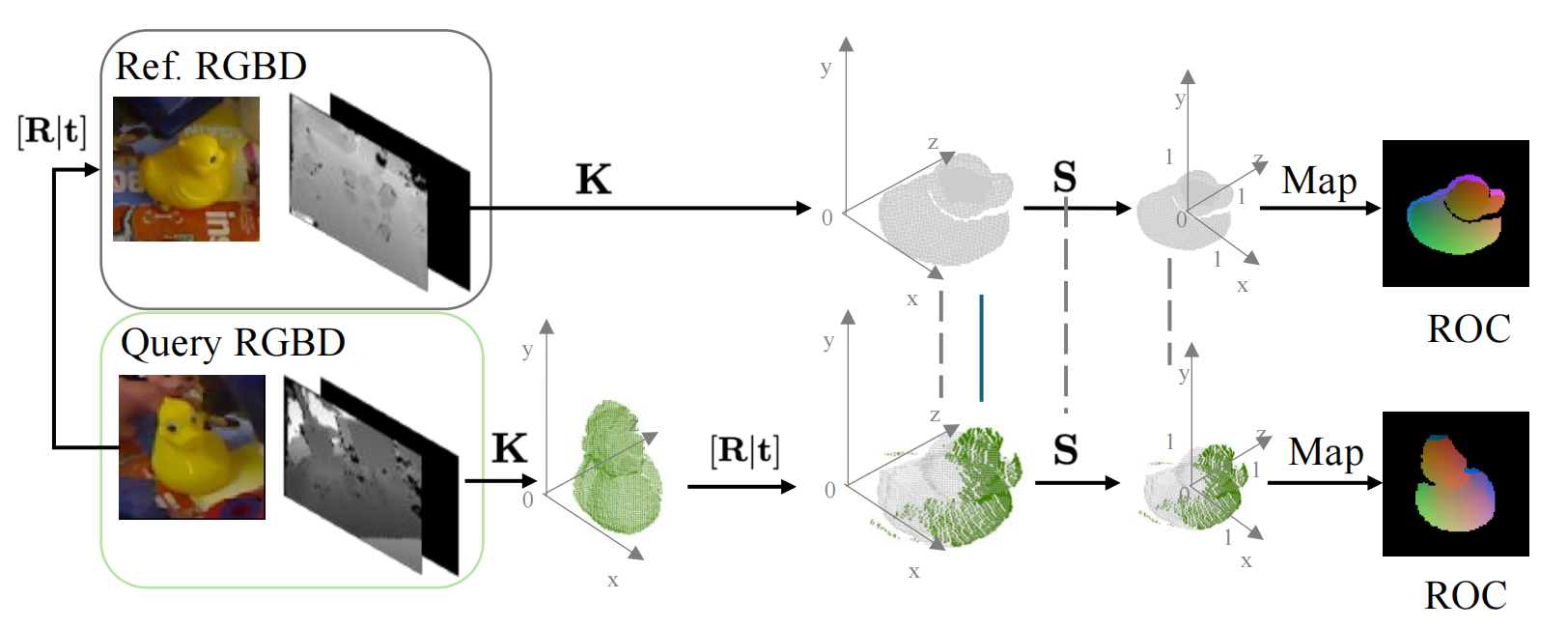图 3：在给定一张参考 RGB-D 图像和一张查询 RGB-D 图像的情况下的 ROC 表示。 ROC 空间首先由参考坐标系定义，并使用相机内参矩阵 K \mathbf{K} K 与缩放矩阵 S \mathbf{S} S 将其映射到一个归一化空间中。随后，利用相对位姿 [ R ∣ t ] [\mathbf{R|t}] [R∣t] 与缩放矩阵 S \mathbf{S} S，将查询图像对齐到该空间。 ROC 映射的生成方式是：将 ROC 空间中的点映射到其对应的 2D 像素位置，并将这些点的位置以 RGB 数值的形式进行编码。

3.3. Reference Object Pose Embedding

1）这一节要解决的"独特难题"是什么？

你现在的任务是： 只给一张参考 RGB-D 图像 A ，就要在任意查询 RGB-D 图像 Q 上估相对位姿（通过预测 ROC，再求 [R|t]）。这里最难的地方在于：参考和查询两张图里，物体看到的部分可能完全不一样，比如：

参考图看到的是物体正面

查询图看到的是侧面，甚至大部分被遮挡

两张图可重叠的可见区域很少

这种情况下，传统"关键点/特征匹配"就很容易死。

2）为什么关键点匹配方法容易失效？（把它讲到你不会再卡）

传统方法（文中说的 keypoint feature matching）大致思路是：

在参考图找一堆关键点（角点、边缘点、局部纹理点）

在查询图找相同的关键点

做匹配（这个点对应那个点）

用对应关系求位姿

问题是：匹配成立的前提是：两张图里要看到"相同区域的相同特征"。

但在你这个设定里：

可见区域重叠少：参考看到的区域，查询可能根本看不到

严重遮挡：关键点可能被挡住

纹理少/重复纹理：关键点不稳定或匹配歧义大

所以匹配直接断链：找不到可靠对应点，后面求位姿就没法做。

在仅给定一张 RGB-D 参考图像的情况下，对查询 RGB-D 图像进行位姿预测是一项具有独特挑战性的任务。以往的方法通常依赖关键点特征匹配 [8, 12, 39]，但当两张图像中可见区域重叠较少或存在严重遮挡时，这类方法往往会失效。我们提出了一种替代方案，将参考图像编码为参考物体位姿嵌入（Reference Object Pose Embedding，ROPE），从而实现有效的物体位姿预测。我们的目标是训练一个参考物体编码器（Reference Object Encoder，ROE），使其能够从单一 RGB-D 参考图像中生成潜空间中的全面物体表示。随后，ROPE 表示使得模型能够在参考相机坐标系中，从该物体的任意测试图像中有效预测 ROC 映射，从而实现精确的位姿估计。

3）他们的替代方案是什么？一句话：把参考图"压缩成一个强条件"，让查询预测时一直"记得参考是谁"

他们不走"点对点匹配"这条路，而是做：

把参考图编码成一个潜空间表示（ROPE），然后查询图在预测 ROC 时始终以这个 ROPE 为条件。

直觉类比：

关键点匹配像：你在两张照片里找"同一个人脸上的同一个痣/眼角"

ROPE 像：你先把参考物体做成一个"完整的身份证档案"（纹理+几何+坐标标签），以后看到它任何一部分，都能凭"身份证"认出来这部分在参考坐标系里是哪。

所以 ROPE 的目标不是"找到对应点"，而是提供一种全局、可泛化、能抗遮挡的参考物体表征。

参考物体编码器 ROE 记为 f ( A ; θ A ) f(A;\theta_A) f(A;θA)，其输入为按通道拼接的张量 A A A，该张量由参考 RGB 图像、参考 ROC 映射以及物体掩码共同组成，用于提取潜空间编码。如图 2 所示，该编码同时捕获了物体的纹理信息和几何信息。编码器通过三层带有残差连接的卷积层 [14] 处理输入，并将生成的特征图划分为若干 patch，同时引入位置嵌入 [1]。这种条件化嵌入能够有效引导 ROC 映射的生成，即便在存在遮挡的情况下，也能保持对参考数据的高度一致性，如第 4.8 节所示。

4）ROPE / ROE 到底是什么？输入输出是什么？（非常关键）

4.1 ROE：Reference Object Encoder（参考物体编码器）

记作： f ( A ; θ A ) f(A;\theta_A) f(A;θA) 它是一个神经网络模块，参数是 θ A \theta_A θA。

4.2 ROPE：Reference Object Pose Embedding（参考物体位姿嵌入）

就是 ROE 的输出：一个潜空间 embedding（可以是向量、也可以是特征图/patch token 序列）。最重要的是：ROPE 被当成条件信息去引导后面的 OPD（解码器）生成查询的 ROC。

5）最容易卡住的点：ROE 的输入为什么不是"参考 RGB-D + mask"，而是"RGB + 参考 ROC + mask"？

原文说 ROE 输入是"按通道拼接的张量 A"，由：

参考 RGB 图像

参考 ROC 映射

物体掩码拼起来。

你可能会懵：参考 ROC 不是我们要预测的东西吗？怎么又拿来当输入？

关键理解：参考 ROC 在参考帧里是可以直接用深度算出来的真值 （上一节 3.2 已经讲了 Y A = S P A Y_A=SP_A YA=SPA）。也就是说：

对参考图：ROC 是"可计算的标签"，不需要网络预测

把它喂给 ROE，相当于明确告诉编码器： "这张参考图里，每个像素对应参考物体坐标系里的哪个 3D 点"

这带来一个巨大的好处：

ROE 不仅看到外观（RGB）和几何（深度隐含在 ROC 里），还直接看到"参考坐标系的定义方式"------也就是物体表面的坐标标注。

于是 ROE 学到的 embedding 会天然绑定"参考坐标系"，这正是后面要用来预测查询 ROC 的关键。

mask 的作用也很明确：

告诉网络哪些像素属于物体，别把背景编码进去污染 embedding。

6）ROE 的网络结构怎么搭？（三层残差卷积 + patch 化 + 位置嵌入）

这一段在讲具体结构：

6.1 三层带残差连接的卷积层（Residual Conv）

卷积的作用：提取局部纹理、边缘、形状线索

残差连接的作用：让深层训练更稳定、不容易梯度消失（这是 ResNet 的核心思想）

虽然只有"三层"，但注意：论文里"三层"往往指"三个 stage/block"，每个 block 里可能还有多层卷积，具体要看图 2 或实现细节。 你只需要抓住： 它用 CNN 提取"参考物体"的特征，并且用残差结构保证训练稳定。

6.2 把特征图划分成 patch

这一步就是把 CNN 输出的 feature map 切成小块（patch），每个 patch 变成一个 token（或一个向量）。直觉：

图像很大，直接把每个像素当 token 太贵

patch 是一种压缩：把局部区域总结成一个 token

6.3 引入位置嵌入（positional embedding）

一旦你把特征变成一堆 patch token，它们本质是一个"集合"。但模型必须知道：

哪个 patch 来自左上角

哪个 patch 来自右下角

不加位置嵌入，patch 顺序信息丢了，空间结构会乱。所以位置嵌入的作用是：

让 embedding 记住"物体各部分在参考图里的空间布局"。

这对于遮挡尤其重要：

你在查询图只看到一小块区域

如果 ROPE 里包含"这块区域在整体里大概是哪"，解码器更容易把它对到正确 ROC 坐标。

7）ROPE 为什么能抗遮挡？别抽象，我给你一个具体直觉

假设参考图里你看到了整只鸭子（图案/形状/ROC坐标都在），ROE 把它编码成 ROPE。现在查询图里鸭子被遮挡，只剩一个边角。如果你用关键点匹配：

那个边角可能没有稳定关键点

或者匹配到错误区域

但用 ROPE + 条件生成 ROC：

OPD 在预测查询 ROC 时，始终"拿着 ROPE 当作模板"

它会把查询图里看到的那点纹理/几何特征映射到 ROPE 中最一致的位置

即使看不全，也能靠"参考物体的整体先验"推断它属于哪一部分

这就是原文说的：

"这种条件化嵌入能够有效引导 ROC 生成，即便遮挡也能保持对参考数据的一致性。"

换句话说： ROPE 提供的是"全局身份与坐标系定义"，而不是"局部点点对应"。

8）把这一节放回整体算法结构里，你应该这样理解它的功能位置

整个系统（按你前面 3.1、3.2 的流程）是：

从参考 RGB-D 计算参考 ROC： Y A Y_A YA

把参考 RGB + 参考 ROC + mask 输入 ROE： e A = f ( A ; θ A ) e_A = f(A;\theta_A) eA=f(A;θA)

查询图进入 OPD（U-Net），并以 e A e_A eA 作为条件，预测查询 ROC： Y ^ Q = g ( Q , e A ; θ Q ) \hat{Y}_Q = g(Q, e_A;\theta_Q) Y^Q=g(Q,eA;θQ)

用 Y ^ Q \hat{Y}_Q Y^Q + 查询深度反投影出来的 3D 点，求相对位姿 [ R ∣ t ] [R|t] [R∣t]

所以 ROE/ROPE 的作用就是：

把参考物体变成一个"可携带的条件信息"，让模型在任何查询视角下都能把物体像素正确地映射回参考坐标（ROC）。

3.4. Object Pose Decoding with ROPE

0）先把一句话讲死：OPD 在干嘛？

OPD 的目标不是直接输出 R , t R,t R,t，而是：

给定查询图像 Q + 参考图像编码得到的 ROPE，输出查询图的 ROC map Y ^ Q \hat{Y}_Q Y^Q。 有了 ROC map，后面就能用几何方法求相对位姿。

所以 OPD 做的是"像素级 3D 坐标回归"：对查询图里属于物体的每个像素，预测一个 3D 坐标（ROC 空间里的 x,y,z）。

物体位姿解码（Object Pose Decoding，OPD）模块 g ( Q , f ; θ Q ) g(Q,f;\theta_Q) g(Q,f;θQ) 基于从参考图像中获得的 ROPE，对查询图像中的物体位姿进行解码。在具有代表性的 ROPE 的强监督条件下，OPD 模块通过为查询图像生成 ROC 映射来预测物体位姿。

1）OPD 的输入输出到底是什么？

输入

查询输入 Q Q Q（至少包含 Q I Q_I QI，以及你前面章节定义的 RGB-D + mask 体系）

参考嵌入 f f f（就是 ROPE，也就是 F A \mathcal{F}^A FA）

在符号上写成： g ( Q , f ; θ Q ) g(Q,f;\theta_Q) g(Q,f;θQ)

输出

预测 ROC map： Y ^ Q ∈ R W × H × 3 \hat{Y}_Q\in\mathbb{R}^{W\times H\times 3} Y^Q∈RW×H×3

OPD 的整体结构采用了受 Stable Diffusion [48] 启发的编码器--解码器架构。

2）OPD 的总体结构：Stable Diffusion 式 encoder--decoder + U-Net 主干

论文说"受 Stable Diffusion 启发的编码器--解码器架构"，你可以理解成一个很标准的套路：

先把查询 RGB 图像编码成特征（不要直接用原始像素）

用一个 U-Net 主干网络 在特征空间里做处理（多尺度、下采样/上采样、skip connection）

在 U-Net 的若干层插入 cross-attention，让网络随时去"参考 ROPE 里查资料"

最后再把特征解码回原图大小，输出 ROC map（三通道）

这跟 Stable Diffusion 很像：SD 也是 U-Net 主干 + cross-attention（条件来自文本）。这里条件不是文本，而是 ROPE（参考物体 embedding）。

为了更好地融合 ROPE 表示，我们引入交叉注意力（cross-attention）层来整合查询图像的信息。具体而言，我们使用文献 [48] 中预训练的 VQVAE 模型对查询 RGB 图像 Q I Q_I QI 进行特征提取，以进一步提升模型的泛化能力。

3）为什么要用预训练的 VQVAE 来抽查询图特征？

论文说：用 [48] 里的预训练 VQVAE 来对查询 RGB 图像 Q I Q_I QI 提特征，增强泛化。人话解释：

预训练的 VQVAE（来自大规模数据）已经学会了"图像里什么是有意义的结构"：边缘、纹理、形状块等

你拿它当一个"很强的图像特征提取器"

这样 OPD 不需要从零学"怎么看图"，只需要学"怎么在这些特征上对齐 ROPE 并输出 ROC"

所以结构上是： Q I → VQVAE encoder F Q Q_I \xrightarrow{\text{VQVAE encoder}} \mathcal{F}^Q QIVQVAE encoder FQ 这里 F Q \mathcal{F}^Q FQ 就是查询特征。

随后，我们在交叉注意力层的条件约束下，对相应的类 U-Net 网络 [48] 进行微调，使其受 ROPE 条件引导。具体结构如图 2 所示。

4）最关键：cross-attention 在这里到底干什么？

你可以把 cross-attention 当成一个"检索器/对齐器"：

U-Net 里每个位置（每个像素/patch 的查询特征）都在问： "我在查询图里看到的这块东西，在参考物体 ROPE 里对应哪里？" 然后从 ROPE 里把对应的信息取出来，融合回查询特征。

这就是它为什么能抗遮挡、抗视角变化：你不是靠局部关键点硬匹配，而是每一层都在做"软对齐 + 信息读取"。

该 U-Net 通过交叉注意力机制，将查询特征 F Q \mathcal{F}^Q FQ 与参考嵌入 F A \mathcal{F}^A FA（即 ROPE）进行融合。更具体地说，在每一层交叉注意力中，查询特征 F Q \mathcal{F}^Q FQ 会与来自 F A \mathcal{F}^A FA 的键向量 k ∈ R m × d k k\in\mathbb{R}^{m\times d_k} k∈Rm×dk 和值向量 v ∈ R m × d v v\in\mathbb{R}^{m\times d_v} v∈Rm×dv 进行交互。

k = F A × W k , v = F A × W v , q = F Q × W q (5) k = \mathcal{F}^A × W_k,\quad v = \mathcal{F}^A × W_v,\quad q = \mathcal{F}^Q × W_q \tag{5} k=FA×Wk,v=FA×Wv,q=FQ×Wq(5)

其中， W W W 表示各向量对应的线性变换权重矩阵。

5）q/k/v 怎么来的？公式(5)讲的是"把两种特征投影成注意力需要的三个向量"

论文写：

k = F A × W k , v = F A × W v , q = F Q × W q (5) k = \mathcal{F}^A × W_k,\quad v = \mathcal{F}^A × W_v,\quad q = \mathcal{F}^Q × W_q \tag{5} k=FA×Wk,v=FA×Wv,q=FQ×Wq(5)

把它翻成人话：

F A \mathcal{F}^A FA：参考特征（ROPE）

F Q \mathcal{F}^Q FQ：查询特征

做三次线性变换（就是全连接/1×1卷积那种）：

从 参考 ROPE 生成：

key（键） k k k

value（值） v v v

从 查询特征 生成：

query（查询） q q q

你可以这样记：

q：我想找什么？（来自查询图）

k：我有哪些"索引标签"？（来自参考 ROPE）

v：我找到以后要取回什么内容？（来自参考 ROPE）

并且论文给了维度：

k ∈ R m × d k k\in\mathbb{R}^{m\times d_k} k∈Rm×dk

v ∈ R m × d v v\in\mathbb{R}^{m\times d_v} v∈Rm×dv

这里 m m m 可以理解成"参考 token 的数量"（比如 ROPE 被 patch 化后有 m 个 token）。

交叉注意力操作作用于 q , k , v q,k,v q,k,v 之间：

Attention ( q , k , v ) = softmax ( q k T d k ) v (6) \text{Attention}(q,k,v) = \text{softmax}\left(\frac{qk^{T}}{\sqrt{d_k}}\right)v \tag{6} Attention(q,k,v)=softmax(dk qkT)v(6)

其中 d k d_k dk 为键向量 k k k 的维度，用于缩放以保证注意力计算中的梯度稳定性。最终得到的相对特征图 F Q 2 A \mathcal{F}^{Q2A} FQ2A 是通过 U-Net 架构 [48] 中多层交叉注意力计算得到的结果。该结构使网络能够充分提取 ROPE 中蕴含的位姿与形状信息。

6）cross-attention 具体怎么算？公式(6)就是标准注意力

Attention ( q , k , v ) = softmax ( q k T d k ) v (6) \text{Attention}(q,k,v) = \text{softmax}\left(\frac{qk^{T}}{\sqrt{d_k}}\right)v \tag{6} Attention(q,k,v)=softmax(dk qkT)v(6)

一步步解释：

6.1 先算相似度： q k T qk^T qkT

q q q 是查询侧的向量（每个位置一个）

k k k 是参考侧的键向量（每个参考 token 一个）

q k T qk^T qkT 得到的是"查询位置 vs 参考 token"的相似度矩阵相似度越大，表示越像、越应该对齐

6.2 为什么除以 d k \sqrt{d_k} dk ？

这叫 scaling，作用是：

维度越大，点积数值会变大，softmax 会过于极端（梯度不稳）

除以 d k \sqrt{d_k} dk 让数值尺度稳定，这是 Transformer 标准做法

6.3 softmax：把相似度变成权重

softmax 后每一行是一个概率分布：

查询位置会把注意力分配到参考 ROPE 的不同 token 上

权重和为 1

6.4 乘以 v：把参考信息"加权读出来"

最后乘 v v v，就得到：

对于查询的每个位置，从参考 ROPE 中读出一个"最相关的摘要信息"

这就是"条件化"的核心：查询特征不再孤立，而是被参考物体的 embedding 指导。

随后，解码器对 F Q 2 A \mathcal{F}^{Q2A} FQ2A进行逐步细化并上采样，将其重建到原始图像的尺寸。该解码器由五个卷积层构成，并配备残差连接与双线性上采样，最终生成 ROC 映射 Y ^ Q \hat{Y}_Q Y^Q；该映射能够在 ROC 空间中准确表示查询视角下的坐标。

7）多层 cross-attention + U-Net，最终得到 F Q 2 A \mathcal{F}^{Q2A} FQ2A

论文说"相对特征图 F Q 2 A \mathcal{F}^{Q2A} FQ2A 是通过 U-Net 中多层 cross-attention 得到的"。你可以理解成：

第一层 cross-attention：粗对齐（大体知道对应哪个区域）

中间层：不断细化（对齐更精确、更局部）

深层：得到一个"已经融合了参考几何/位姿信息"的查询特征

所以 F Q 2 A \mathcal{F}^{Q2A} FQ2A 的含义就是：

Query features conditioned on (aligned to) Reference embedding 基于（对齐到）参考嵌入的查询特征

ROC map loss. 按照 NOCS [55] 的做法，我们使用平滑 L1 损失（Smooth L1 Loss）[47]，以 ROC 真值映射 Y Q Y_Q YQ 对预测结果 Y ^ Q \hat{Y}_Q Y^Q 进行监督，从而训练网络 { f , g } \{f,g\} {f,g}：

L = 1 N ∑ i ∑ j Q M ( i , j ) E ( i , j ) c = Y Q ( i , j ) − Y ^ Q ( i , j ) E ( i , j ) = { 0.5 c 2 / β , ∣ c ∣ < β ∣ c ∣ − 0.5 β , otherwise (7) \begin{aligned} \mathcal{L} &= \frac{1}{N}\sum_i\sum_j Q_M(i,j)E(i,j) \\ c &= Y_Q(i,j)-\hat{Y}_Q(i,j) \\ E(i,j) &= \begin{cases} 0.5c^2/\beta, & |c|<\beta \\ |c|-0.5\beta, & \text{otherwise} \end{cases} \end{aligned} \tag{7} LcE(i,j)=N1i∑j∑QM(i,j)E(i,j)=YQ(i,j)−Y^Q(i,j)={0.5c2/β,∣c∣−0.5β,∣c∣<βotherwise(7)

其中 β \beta β 为平滑阈值，设置为 0.1。对于物体掩码区域的像素位置， Q M ( i , j ) = 1 Q_M(i,j)=1 QM(i,j)=1，否则为 0。

8）解码器怎么输出 ROC map？------逐步上采样回原图大小，最后输出 3 通道坐标

论文说解码器：

5 个卷积层

残差连接

双线性上采样

输出 Y ^ Q \hat{Y}_Q Y^Q

直觉很简单：

现在的特征图可能是低分辨率（U-Net 下采样后的）

逐层上采样（分辨率变大）

每次上采样后用卷积"修细节"

最后得到跟输入图同尺寸的输出

输出通道数是 3（x,y,z）

为什么是 3？因为 ROC 每个像素要预测一个 3D 坐标。

9）ROC map loss：为什么用 Smooth L1？它到底怎么监督？

论文给的 loss：

L = 1 N ∑ i ∑ j Q M ( i , j ) E ( i , j ) c = Y Q ( i , j ) − Y ^ Q ( i , j ) E ( i , j ) = { 0.5 c 2 / β , ∣ c ∣ < β ∣ c ∣ − 0.5 β , otherwise (7) \begin{aligned} \mathcal{L} &= \frac{1}{N}\sum_i\sum_j Q_M(i,j)E(i,j) \\ c &= Y_Q(i,j)-\hat{Y}_Q(i,j) \\ E(i,j) &= \begin{cases} 0.5c^2/\beta, & |c|<\beta \\ |c|-0.5\beta, & \text{otherwise} \end{cases} \end{aligned} \tag{7} LcE(i,j)=N1i∑j∑QM(i,j)E(i,j)=YQ(i,j)−Y^Q(i,j)={0.5c2/β,∣c∣−0.5β,∣c∣<βotherwise(7)

9.1 先讲 mask：只在物体区域算损失

Q M ( i , j ) Q_M(i,j) QM(i,j) 是查询 mask：

物体像素 = 1

背景像素 = 0

所以背景不会参与 loss。这非常合理：背景没有 ROC 坐标意义，硬算会把网络带偏。

9.2 Smooth L1 是什么直觉？

它是 L2 和 L1 的折中：

误差小的时候用平方（像 L2）：

梯度平滑，收敛稳定

误差大时候用绝对值（像 L1）：

对离群点更鲁棒，不会被特别大的错误主导

这对 ROC 回归非常合适，因为：

预测初期可能错得很离谱（用 L2 会爆炸）

后期要精细对齐（L1 不够平滑）

β = 0.1 \beta=0.1 β=0.1 是切换阈值：

小于 0.1：当作小误差，用二次

大于 0.1：当作大误差，用一次

10）把 OPD 这一节总结成你脑子里能跑的"算法流水线"

你现在可以这样理解整个 OPD：

用预训练 VQVAE 编码查询 RGB 图像，得到查询特征 F Q \mathcal{F}^Q FQ

参考图经过 ROE 得到 ROPE 特征 F A \mathcal{F}^A FA

把 F Q \mathcal{F}^Q FQ 喂给 U-Net，在多层插入 cross-attention：

q 来自查询特征

k,v 来自参考 ROPE

attention 让查询每个位置从参考中读取最相关信息

得到融合后的特征 F Q 2 A \mathcal{F}^{Q2A} FQ2A

解码器上采样输出 ROC map Y ^ Q \hat{Y}_Q Y^Q

用 Smooth L1 + mask 监督 Y ^ Q \hat{Y}_Q Y^Q 接近真值 Y Q Y_Q YQ

训练好后，推理时：

只要给参考图（可算 Y A Y_A YA）→ 得到 ROPE

给查询图 → 输出 Y ^ Q \hat{Y}_Q Y^Q

再用几何求解得到 [ R ∣ t ] [R|t] [R∣t]

3.5. Pose Estimation from ROC Map

相对位姿 [ R ∣ t ] \mathbf{[R|t]} [R∣t] 通过计算预测的 ROC 映射 Y ^ Q \hat{Y}_Q Y^Q 与查询视角点云 P Q P_Q PQ 之间的变换关系获得。需要注意的是，参考相机位姿被设定为 [ I 3 ∣ 0 ] \mathbf{[I_3|0]} [I3∣0]。首先，我们使用参考 ROC 的缩放矩阵逆 S − 1 \mathbf{S}^{-1} S−1，对预测的 ROC Y ^ Q \hat{Y}_Q Y^Q 进行反缩放和平移，使其对齐到参考相机坐标系中。由此得到的点云 P ^ Q A \hat{P}_Q^A P^QA 表示查询物体在参考相机坐标系下的点云。随后，我们利用查询点云 P Q P_Q PQ，通过 Umeyama 算法 [53] 计算查询坐标系与参考坐标系之间的位姿预测 [ R ^ ∣ t ^ ] \mathbf{[\hat{R}|\hat{t}]} [R^∣t^]。

P ^ Q A = S − 1 Y ^ Q [ Q M = 1 ] [ R ^ ∣ t ^ ] = Umeyama ( P Q , P ^ Q A ) (8) \begin{aligned} \hat{P}_Q^A &= \mathbf{S}^{-1}\hat{Y}_Q[Q_M=1] \\ [\hat{\mathbf{R}}|\hat{\mathbf{t}}] &= \textbf{Umeyama}(P_Q,\hat{P}_Q^A) \end{aligned} \tag{8} P^QA[R^∣t^]=S−1Y^Q[QM=1]=Umeyama(PQ,P^QA)(8)

1）这一节的核心任务：从"像素预测"变回"刚体位姿"

前面网络输出的是：

Y ^ Q ∈ R W × H × 3 \hat{Y}_Q\in\mathbb{R}^{W\times H\times 3} Y^Q∈RW×H×3：查询图的预测 ROC map（每个像素一个 3D 坐标，但在 ROC 归一化空间里）

你真正想要的是：相对位姿 [ R ^ ∣ t ^ ] [\hat{R}|\hat{t}] [R^∣t^]（把查询坐标系的点变到参考坐标系）

这一步就是：把 Y ^ Q \hat{Y}_Q Y^Q 变成可用的 3D 点，然后用几何法求 R , t R,t R,t。

2）先钉死坐标系：参考相机位姿为什么设为 [ I 3 ∣ 0 ] [I_3|0] [I3∣0]？

原文说：

参考相机位姿被设定为 [ I 3 ∣ 0 ] [I_3|0] [I3∣0]

这不是在说"相机真的不动"，而是在做一个常见的数学约定：

既然我们估计的是"查询相对于参考"的相对位姿

那就把参考坐标系当作"世界原点"

在这个世界里，参考相机坐标系就是单位变换：旋转是单位矩阵 I 3 I_3 I3，平移是 0

这样做的好处是：

省掉一层坐标变换

你解出来的 [ R ^ ∣ t ^ ] [\hat{R}|\hat{t}] [R^∣t^] 就直接表示"查询→参考"的变换

3）最关键一步：为什么要用 S − 1 S^{-1} S−1？------因为网络输出在"归一化ROC空间"，不是米单位的相机坐标

在 3.2 你已经学过：

ROC 是用一个缩放+平移矩阵 S S S 把点云归一化得到的 Y = S P Y = S P Y=SP 所以网络预测的 Y ^ Q \hat{Y}_Q Y^Q 本质上是在 ROC 空间（例如 [ 0 , 1 ] 3 [0,1]^3 [0,1]3 这种范围）。

但你要用 Umeyama 配准，必须在真实几何空间（相机坐标系）里做 3D 点配准，否则尺度/平移都不对。因此必须把 Y ^ Q \hat{Y}_Q Y^Q "还原"回参考相机坐标系下的 3D 点：

P = S − 1 Y P = S^{-1}Y P=S−1Y

这就是文中说的"反缩放和平移"。

一句话理解：

S S S 把真实 3D 点压进标准盒子； S − 1 S^{-1} S−1 把盒子里的坐标还原回真实 3D 空间。

4） P ^ Q A \hat{P}_Q^A P^QA 是什么？------"查询物体在参考相机坐标系下的点云（网络预测出来的）"

他们定义：

P ^ Q A = S − 1 Y ^ Q [ Q M = 1 ] \hat{P}_Q^A = S^{-1}\hat{Y}_Q[Q_M=1] P^QA=S−1Y^Q[QM=1]

拆开解释：

4.1 为什么要 [ Q M = 1 ] [Q_M=1] [QM=1]？

因为 ROC map 对背景像素没意义。只取 mask 为 1 的像素，也就是"物体区域"。

4.2 这一步到底得到什么？

对每个物体像素 ( i , j ) (i,j) (i,j)：

你有一个预测的 ROC 坐标 Y ^ Q ( i , j ) = ( x , y , z ) \hat{Y}_Q(i,j)=(x,y,z) Y^Q(i,j)=(x,y,z)

用 S − 1 S^{-1} S−1 变换回参考相机坐标系下的真实 3D 点

把所有物体像素的 3D 点收集起来，就是一个点云： P ^ Q A \hat{P}_Q^A P^QA

它名字里的 " A ^A A" 表示：在参考（A）的坐标系里表达。所以：

P ^ Q A \hat{P}_Q^A P^QA = 网络根据查询图预测出来的"物体点云"，但已经被放到了参考相机坐标系下。

这句话非常关键，因为它说明网络输出实际上已经隐含了"对齐到参考"的信息。

5） P Q P_Q PQ 是什么？------"查询相机坐标系里真实测到的物体点云"

P Q P_Q PQ 来自查询 RGB-D 的深度反投影（你前面已经看过同样的操作）：

用 Q D Q_D QD + 相机内参 K K K

对 mask 为 1 的像素做反投影得到查询相机坐标系下的物体点云：

P Q = K − 1 Q D [ Q M = 1 ] P_Q = K^{-1}Q_D[Q_M=1] PQ=K−1QD[QM=1]

（论文这节没重写公式，但就是这个意思。）所以：

P Q P_Q PQ：真实观测点云（查询坐标系）

P ^ Q A \hat{P}_Q^A P^QA：预测点云（参考坐标系）

6）现在问题就变成一个超级经典的几何问题：3D-3D 刚体配准

你有两堆点：

源点云： P Q P_Q PQ（在查询坐标系）

目标点云： P ^ Q A \hat{P}_Q^A P^QA（在参考坐标系）

你要找一个刚体变换 [ R ^ ∣ t ^ ] [\hat{R}|\hat{t}] [R^∣t^]，使得：

R ^ , P Q + t ^ ≈ P ^ Q A \hat{R},P_Q + \hat{t} \approx \hat{P}_Q^A R^,PQ+t^≈P^QA

这就是"点云配准"，而 Umeyama 算法就是用闭式解（SVD）来求这个最小二乘意义下的 R , t R,t R,t（并且它也能处理尺度，但这里你要的是刚体，所以通常固定尺度为 1 或使用其不带尺度的版本；论文引用 Umeyama 用于求位姿。）

7）Umeyama 算法到底做了啥？------一句话：用 SVD 找最优旋转，再补平移

你不用记所有推导，但必须懂它在做哪几件事：

算两堆点的质心（平均位置）

把两堆点都"去中心化"（减掉各自质心）

算它们的协方差矩阵

对协方差做 SVD，得到最优旋转 R ^ \hat{R} R^

用质心关系得到平移 t ^ \hat{t} t^

它的优势是：

不需要迭代（不像 ICP 反复对齐）

数学上有闭式最优解

很快、很稳定

所以这一步就像"最后一脚"：把网络给的对应关系凝聚成一个 6D 位姿。

8）公式 (8) 逐行"人话翻译"

论文给：

P ^ Q A = S − 1 Y ^ Q [ Q M = 1 ] [ R ^ ∣ t ^ ] = Umeyama ( P Q , P ^ Q A ) (8) \begin{aligned} \hat{P}_Q^A &= \mathbf{S}^{-1}\hat{Y}_Q[Q_M=1] \\ [\hat{\mathbf{R}}|\hat{\mathbf{t}}] &= \textbf{Umeyama}(P_Q,\hat{P}_Q^A) \end{aligned} \tag{8} P^QA[R^∣t^]=S−1Y^Q[QM=1]=Umeyama(PQ,P^QA)(8)

逐行解释：

第一行

从预测 ROC map 中拿出物体像素，

用 S − 1 S^{-1} S−1 把 ROC 空间坐标还原到参考相机坐标系，

得到预测的参考系点云 P ^ Q A \hat{P}_Q^A P^QA。

第二行

把"查询系真实点云 P Q P_Q PQ"和"参考系预测点云 P ^ Q A \hat{P}_Q^A P^QA"喂给 Umeyama，

算出最能把 P Q P_Q PQ 对齐到 P ^ Q A \hat{P}_Q^A P^QA 的旋转和平移

输出 [ R ^ ∣ t ^ ] [\hat{R}|\hat{t}] [R^∣t^]。

9）最容易卡住的 4 个点，我直接给你讲透

卡点1：为什么能把 Y ^ Q \hat{Y}_Q Y^Q 当点云？它不是图吗？

它是图，但对 mask 为 1 的像素，每个像素都有一个 3D 坐标（三通道），把这些 3D 坐标收集起来就是点云。 "图"只是存储形式，"点云"是内容本质。

卡点2： P ^ Q A \hat{P}_Q^A P^QA 为什么说在参考坐标系？

因为 ROC 的定义本来就"以参考为锚点"，并且你用 S − 1 S^{-1} S−1还原得到的是"参考相机坐标系中的坐标"。所以它天然落在参考系。

卡点3： P Q P_Q PQ 和 P ^ Q A \hat{P}_Q^A P^QA 有一一对应吗？

严格来说像素级上是对应的：同一个像素位置既能反投影出 P Q P_Q PQ 的点，也有 Y ^ Q \hat{Y}_Q Y^Q 给出的对应坐标。所以可以把它们当成一组对应点集来解配准（非常关键：这就是为什么能用 Umeyama 而不是 ICP）。

卡点4：为什么不用 ICP？

因为 ICP 需要反复找最近邻，慢且对初值敏感。这里网络已经给出了"每个像素对应的参考坐标"，相当于直接给了对应关系，用 Umeyama 一步闭式解更直接更稳。

10）把这节变成你能写代码的"最短流程"

用 mask 取出物体像素索引集合 Ω = ( i , j ) ∣ Q M ( i , j ) = 1 \Omega={(i,j)\mid Q_M(i,j)=1} Ω=(i,j)∣QM(i,j)=1

构造两堆点：

查询真实点：从深度反投影得到 P Q P_Q PQ

参考系预测点： P ^ Q A = S − 1 Y ^ Q [ Ω ] \hat{P}_Q^A=S^{-1}\hat{Y}_Q[\Omega] P^QA=S−1Y^Q[Ω]

调 Umeyama / SVD 求刚体变换，得到 [ R ^ ∣ t ^ ] [\hat{R}|\hat{t}] [R^∣t^]