自强制:弥合自回归视频扩散中的训练--测试差距
paper title:Self Forcing: Bridging the Train-Test Gap in
Autoregressive Video Diffusion
paper是Adobe发表在NIPS 2025的工作
Code:链接
Abstract
我们提出了 Self Forcing,一种用于自回归视频扩散模型的全新训练范式。该方法针对长期存在的曝光偏置问题:模型在训练时依赖真实上下文,而在推理阶段却必须基于自身并不完美的生成结果来生成序列。不同于以往在真实上下文帧条件下对未来帧进行去噪的方法,Self Forcing 在训练过程中通过带有键值(KV)缓存的自回归展开,使每一帧的生成都条件于此前由模型自身生成的输出。该策略使得可以在视频层面通过整体损失进行监督,直接评估完整生成序列的质量,而不再仅依赖传统的逐帧目标函数。为保证训练效率,我们采用了少步扩散模型,并结合随机梯度截断策略,在计算开销与性能之间取得有效平衡。此外,我们还引入了一种滚动式 KV 缓存机制,实现了高效的自回归视频外推。大量实验表明,我们的方法在单张 GPU 上即可实现亚秒级延迟的实时流式视频生成,同时在生成质量上能够达到甚至超过显著更慢且非因果的扩散模型。
1 Introduction
近年来,视频合成领域取得了巨大的进展,最先进的系统已经能够生成具有复杂时间动态的高度逼真内容 [6]。然而,这些成果通常依赖于扩散 Transformer(DiT)[62, 83],其通过双向注意力同时对所有帧进行去噪。这种设计允许未来影响过去,并且要求一次性生成完整视频,从根本上限制了其在实时流式应用中的适用性,因为在生成当前帧时未来信息是未知的。相比之下,自回归(AR)模型 [17, 27, 38, 94, 104] 按时间顺序逐帧生成视频,这一范式天然契合时间媒体的因果结构。这种方法不仅显著降低了生成视频的观看延迟,还解锁了众多应用场景,包括实时交互式内容创作 [9, 46]、游戏模拟 [11, 61, 78, 102] 以及机器人学习 [42, 96, 101]。然而,由于依赖有损的向量量化技术 [79],AR 模型在视觉保真度上往往难以达到最先进视频扩散模型的水平。
为了兼具两者的优势,近年来出现了两种为视频扩散模型引入 AR 生成能力的技术:Teacher Forcing(TF)[16, 28, 33, 106] 和 Diffusion Forcing(DF)[8, 10, 20, 69, 73, 100]。Teacher Forcing 是序列建模中一种成熟的范式,其训练模型在真实标注序列条件下预测下一个标记。应用于视频扩散时,TF 通过使用干净的真实上下文帧对每一帧进行去噪(图 1(a)),这一策略通常被称为下一帧预测。相比之下,Diffusion Forcing 在训练时为每一帧独立采样噪声水平,使模型基于带噪的上下文帧对当前帧进行去噪(图 1(b))。这保证了训练分布覆盖了自回归推理场景,即上下文帧是干净的而当前帧是带噪的。
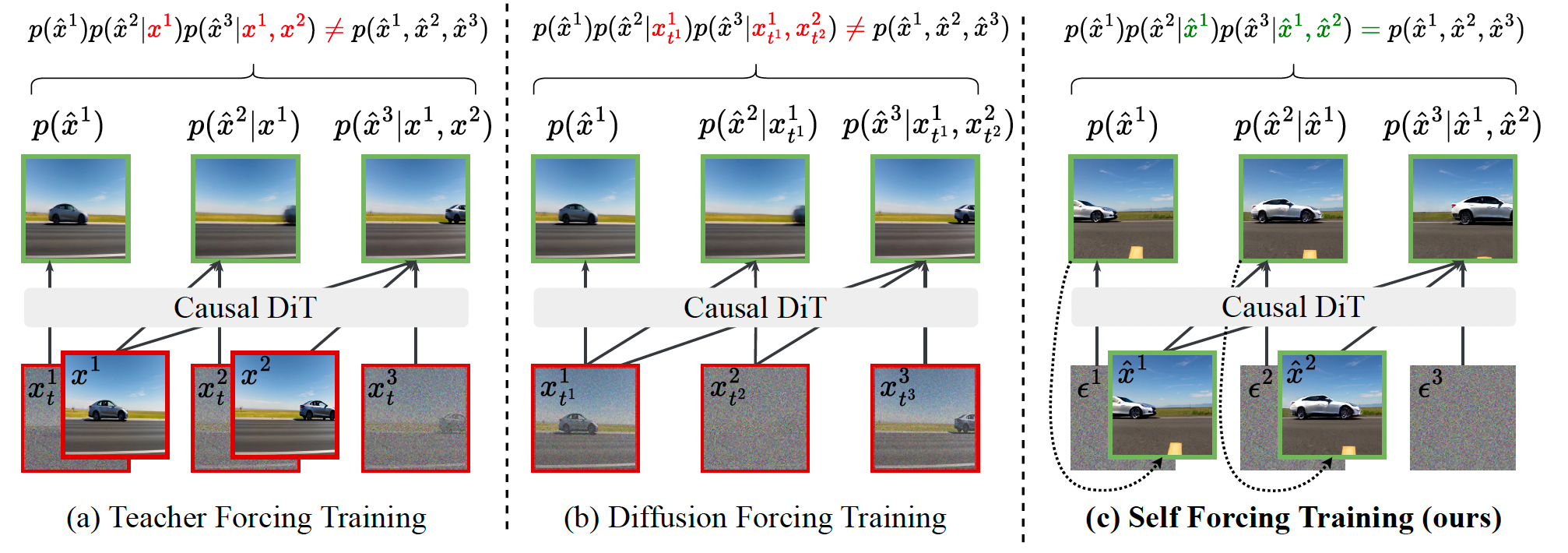
图 1:自回归视频扩散模型的训练范式。(a) 在 Teacher Forcing 中,模型被训练为在前序干净、真实的上下文帧条件下,对每一帧进行去噪。(b) 在 Diffusion Forcing 中,模型被训练为在具有不同噪声水平的前序上下文帧条件下,对每一帧进行去噪。(a) 和 (b) 所生成的输出均不属于模型在推理阶段实际生成的分布。© 我们提出的 Self Forcing 方法在训练过程中执行自回归的自展开,根据由模型自身生成的先前上下文帧来对下一帧进行去噪。在最终生成的视频上计算分布匹配损失(例如 SiD、DMD、GAN),以使生成视频的分布与真实视频的分布对齐。我们的训练范式高度贴合推理过程,从而弥合了训练--测试阶段的分布差距。
然而,采用 TF 或 DF 训练的模型在自回归生成过程中往往会遭遇误差累积问题,导致视频质量随时间推移而退化 [84, 100, 105]。这一问题在更广泛的意义上被称为曝光偏置 [60, 71]:模型在训练时仅接触真实上下文,而在推理时却必须依赖自身并不完美的预测,从而产生分布不匹配,并在生成过程中不断放大误差。尽管一些方法试图在推理阶段通过引入带噪上下文帧来缓解视频扩散模型中的这一问题 [8, 11, 105],但这种设计会牺牲时间一致性,增加 KV 缓存设计的复杂度,提高生成延迟,并且并未从根本上解决曝光偏置问题。
在本文中,我们提出了 Self Forcing(SF),一种用于解决自回归视频生成中曝光偏置问题的新算法。该方法受到早期 RNN 时代序列建模技术 [40, 65, 103] 的启发,通过在训练过程中显式展开自回归生成过程,使每一帧的生成都条件于先前由模型自身生成的帧,而非真实帧,从而弥合训练与测试阶段的分布差距。这使得可以在完整生成的视频序列上施加整体性的分布匹配损失 [18, 98, 99]。通过迫使模型直面并学习自身预测误差,Self Forcing 有效缓解了曝光偏置并减少了误差累积。
尽管由于其顺序生成特性无法并行训练,Self Forcing 乍看之下计算开销巨大,但我们表明它可以作为一种后训练阶段的算法高效实现,此时模型无需大量梯度更新即可收敛。通过采用少步扩散骨干网络以及精心设计的梯度截断策略,Self Forcing 在相同的实际训练时间内反而比其他并行策略更加高效,并取得了更优的性能。此外,我们还引入了一种滚动式 KV 缓存机制,进一步提升了视频外推的效率。
大量实验表明,我们的模型在单张 H100 GPU 上即可实现 17 FPS、亚秒级延迟的实时视频生成,同时在生成质量上与近期缓慢的双向和自回归视频扩散模型相比具有竞争力甚至更优。这些进展为真正的交互式视频生成应用打开了大门------如直播、游戏和世界模拟------在这些场景中,延迟预算以毫秒而非分钟来衡量。
2 Related Work
用于视频生成的 GAN。早期的视频生成方法主要依赖生成对抗网络(GAN)[18],要么使用卷积网络并行生成完整视频 [5, 68, 82],要么采用循环结构按序生成视频帧 [14, 44, 49, 77, 81]。近年来,GAN 也被用于蒸馏视频扩散模型 [47, 56, 91, 108]。由于 GAN 中的生成器在训练和推理阶段遵循相同的生成过程,其天然避免了曝光偏置问题。我们的工作从这一 GAN 的基本原理中获得启发,通过直接优化生成器输出分布与目标分布之间的对齐来进行训练。
用于视频生成的自回归 / 扩散模型。现代视频生成模型由于更强的尺度扩展能力,已在很大程度上转向扩散模型或自回归模型。视频扩散模型通常采用双向注意力机制,同时对所有视频帧进行去噪 [3, 4, 6, 13, 23--26, 39, 64, 80, 83, 97]。相比之下,自回归模型以预测下一个标记为训练目标,并在推理阶段按顺序生成时空标记 [7, 38, 66, 86, 88, 94]。
自回归--扩散混合模型。最近,将自回归与扩散框架相结合的混合模型作为视频生成 [8, 16, 20, 22, 28, 33, 45, 50, 52, 89, 100, 106, 107] 以及其他序列领域 [1, 12, 43, 53, 59, 90, 110] 中一种有前景的生成建模方向受到关注。这类方法通常依赖较长的迭代预测链(在时间上是自回归的,在空间上是逐步去噪的),从而可能导致显著的误差累积。我们的工作通过在训练时让模型条件于自身预测,并教会其纠正自身错误,从而应对这一问题。
滚动扩散及其变体。另一类工作 [35, 67, 69, 76, 93, 105] 使用渐进式噪声调度来训练视频扩散模型,其中噪声水平从较早的帧逐渐增加到较晚的帧。尽管这些方法支持以较少误差累积的方式进行顺序长视频生成,并且有时也被称为自回归方法,但它们并未严格遵循自回归的链式法则分解。因此,在交互式应用中会表现出显著的延迟,因为在当前帧呈现给用户之前,未来帧已被部分预生成。这种过早的承诺限制了实时用户注入控制的影响,使得紧随其后的帧响应能力受限。
CausVid。我们的工作与 CausVid [100] 关系最为密切。CausVid 使用 DF 方案和分布匹配蒸馏(DMD)来训练少步自回归扩散模型。然而,CausVid 存在一个关键缺陷:其训练输出(通过 DF 生成)并不来自模型在推理阶段实际产生的分布,因此 DMD 损失实际上匹配的是错误的分布。我们明确指出了这一问题,并提出了一种能够匹配真实模型分布的解决方案。
3 Self Forcing: Briding Train-Test Gap via Holistic Post-Training
我们首先在第 3.1 节中给出自回归视频扩散模型的形式化定义,并介绍标准的训练方法。在第 3.2 节中,我们介绍 Self Forcing 训练算法的核心内容,并说明如何利用少步扩散模型对其进行高效实现。在第 3.3 节中,我们讨论多种整体性的、视频层面的分布匹配训练目标。最后,在第 3.4 节中,我们引入一种滚动式键值缓存机制,使得任意长度视频的高效生成成为可能。
3.1 Preliminaries: Autoregressive Video Diffusion Models
自回归视频扩散模型是一种混合生成模型,它将自回归的链式法则分解与去噪扩散模型相结合,用于视频生成。具体而言,给定由 N N N 帧视频组成的序列 x 1 : N = ( x 1 , x 2 , ... , x N ) x^{1:N} = (x^1, x^2, \ldots, x^N) x1:N=(x1,x2,...,xN),其联合分布可以通过链式法则分解为条件分布的乘积:
p ( x 1 : N ) = ∏ i = 1 N p ( x i ∣ x < i ) . p(x^{1:N}) = \prod_{i=1}^N p(x^i \mid x^{< i}) . p(x1:N)=i=1∏Np(xi∣x<i).
随后,每一个条件分布 p ( x i ∣ x < i ) p(x^i \mid x^{< i}) p(xi∣x<i) 都通过一个扩散过程进行建模,其中当前帧是在已生成帧的条件下,通过逐步对初始高斯噪声进行去噪而生成的。该形式同时结合了自回归模型在建模序列依赖关系方面的优势,以及扩散模型在连续值视觉信号高质量生成方面的能力。在实际应用中,我们也可以选择一次生成一段帧块,而不是单帧生成 [69, 100]。不过为了符号表示的简洁性,在本节中我们仍将每个帧块记作一帧。
现有的大多数自回归视频扩散模型通常在 Teacher Forcing(TF)或 Diffusion Forcing(DF)的范式下,采用逐帧去噪损失进行训练。具体来说,每一帧 x i x^i xi 都会通过前向扩散过程 q t i ∣ 0 ( x t i i ∣ x 0 i ) q_{t^i \mid 0}(x_{t^i}^i \mid x_0^i) qti∣0(xtii∣x0i) 被扰动,使得
x t i i = Ψ ( x i , ϵ i , t i ) = α t i x i + σ t i ϵ i , x_{t^i}^i = \Psi(x^i, \epsilon^i, t^i) = \alpha_{t^i} x^i + \sigma_{t^i} \epsilon^i , xtii=Ψ(xi,ϵi,ti)=αtixi+σtiϵi,
其中 α t i , σ t i \alpha_{t^i}, \sigma_{t^i} αti,σti 是在有限时间范围 t i ∈ [ 0 , 1000 ] t^i \in [0, 1000] ti∈[0,1000] 内预定义的噪声调度参数,且 ϵ i ∼ N ( 0 , I ) \epsilon^i \sim \mathcal{N}(0, I) ϵi∼N(0,I) 为高斯噪声。在 TF 中,时间步 t i t^i ti 通常在所有帧之间共享;而在 DF 中,则为每一帧独立采样时间步。生成模型通过对前向过程的时间反演来学习,其中每一步去噪可以通过神经网络预测加入到该帧中的噪声来实现,即
ϵ ^ θ i : = G θ ( x t i i , t i , c ) , \hat{\epsilon}\theta^i := G\theta(x_{t^i}^i, t^i, c) , ϵ^θi:=Gθ(xtii,ti,c),
该网络在上下文 c c c 的条件下进行预测。在 TF 中,上下文由干净的真实帧 x < i x^{< i} x<i 构成;而在 DF 中,上下文则由带噪的上下文帧 x t j j , j < i x_{t_j}^j,\, j< i xtjj,j<i 构成。模型通过最小化预测噪声与真实噪声之间的逐帧均方误差(MSE)进行训练:
L θ D M = E x i , t i , ϵ i [ w t i ∥ ϵ ^ θ i − ϵ i ∥ 2 2 ] , \mathcal{L}\theta^{\mathrm{DM}} = \mathbb{E}{x^i, t^i, \epsilon^i} \left[ w_{t^i} \left\| \hat{\epsilon}_\theta^i - \epsilon^i \right\|_2^2 \right] , LθDM=Exi,ti,ϵi[wti ϵ^θi−ϵi 22],
其中 w t i w_{t^i} wti 为加权函数。
我们关注的是一种基于 Transformer 的扩散模型架构 [62],该模型带有文本条件(为清晰起见在公式中省略),并在由因果 3D 变分自编码器(VAE)[37] 编码得到的压缩潜空间中运行。自回归的链式法则分解通过因果注意力机制来实现。图 2(a) 和 (b) 展示了 Teacher Forcing 与 Diffusion Forcing 方法中注意力掩码的配置方式。对于 Teacher Forcing,我们描述了一种高效的变体,其通过块稀疏注意力掩码并行处理所有帧,而非在每次训练迭代中只对单帧进行去噪 [33]。这种设计已被用于基于 MAR 的自回归视频生成方法 [43, 111],并同时应用于其他自回归视频扩散模型中 [106, 107]。
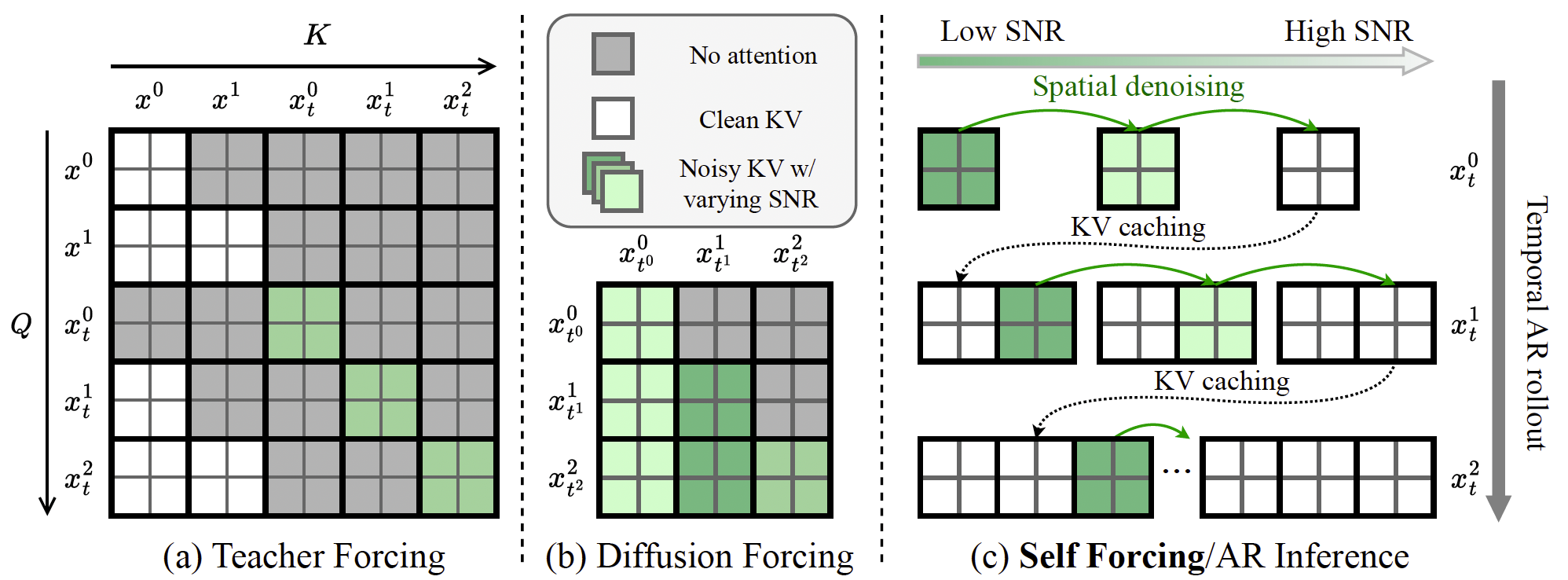
图 2:注意力掩码配置。Teacher Forcing(a)和 Diffusion Forcing(b)均在整个视频上并行训练模型,并通过定制的注意力掩码来强制因果依赖关系。相比之下,我们的 Self-Forcing 训练方式(c)通过使用 KV 缓存来复现自回归(AR)推理过程,而不依赖任何特殊的注意力掩码。为便于说明,我们展示了一个视频包含 3 帧、且每一帧由 2 个标记组成的示例场景。
3.2 Autoregressive Diffusion Post-Training via Self-Rollout
Self Forcing 的核心思想是在训练过程中遵循推理阶段的生成流程,通过自回归的自展开来生成视频。具体而言,我们从模型分布中采样一批视频 { x θ 1 : N } ∼ p θ ( x 1 : N ) = ∏ i = 1 N p θ ( x i ∣ x < i ) \{x_\theta^{1:N}\} \sim p_\theta(x^{1:N}) = \prod_{i=1}^N p_\theta(x^i \mid x^{< i}) {xθ1:N}∼pθ(x1:N)=∏i=1Npθ(xi∣x<i),其中每一帧 x i x^i xi 都是在自生成输出的条件下,通过迭代去噪得到的,这些自生成输出既包括过去的干净上下文帧,也包括当前时间步的带噪帧。不同于以往大多数仅在推理阶段使用 KV 缓存的自回归模型,我们的 Self Forcing 方法创新性地在训练阶段引入了 KV 缓存,如图 2© 所示。
然而,若直接使用标准的多步扩散模型来实现 Self Forcing,在计算上将是不可承受的,因为这需要对冗长的去噪链进行展开并反向传播。因此,我们选择使用少步扩散模型 G θ G_\theta Gθ 来近似自回归分解中每一个条件分布 p θ ( x i ∣ x < i ) p_\theta(x^i \mid x^{< i}) pθ(xi∣x<i)。考虑时间步集合 { t 0 = 0 , t 1 , ... , t T = 1000 } \{t_0 = 0, t_1, \ldots, t_T = 1000\} {t0=0,t1,...,tT=1000},这是区间 [ 0 , ... , 1000 ] [0, \ldots, 1000] [0,...,1000] 的一个子序列。在每一个去噪步骤 t j t_j tj 和帧索引 i i i 处,模型在先前干净帧 x < i x^{< i} x<i 的条件下,对中间的带噪帧 x t j i x_{t_j}^i xtji 进行去噪。随后,模型通过前向过程 Ψ \Psi Ψ 向去噪后的帧中重新注入较低噪声水平的高斯噪声,从而得到作为下一去噪步骤输入的带噪帧 x t j − 1 i x_{t_{j-1}}^i xtj−1i,这一过程遵循少步扩散模型中的标准做法 [74, 98]。模型分布 p θ ( x i ∣ x < i ) p_\theta(x^i \mid x^{< i}) pθ(xi∣x<i) 被隐式地定义为
f θ , t 1 ∘ f θ , t 2 ∘ ⋯ ∘ f θ , t T ( x t T i ) , f_{\theta,t_1} \circ f_{\theta,t_2} \circ \cdots \circ f_{\theta,t_T}(x_{t_T}^i), fθ,t1∘fθ,t2∘⋯∘fθ,tT(xtTi),
其中
f θ , t j ( x t j i ) = Ψ ( G θ ( x t j i , t j , x < i ) , ϵ t j − 1 , t j − 1 ) , f_{\theta,t_j}(x_{t_j}^i) = \Psi\bigl(G_\theta(x_{t_j}^i, t_j, x^{< i}), \epsilon_{t_{j-1}}, t_{j-1}\bigr), fθ,tj(xtji)=Ψ(Gθ(xtji,tj,x<i),ϵtj−1,tj−1),
并且 x t T i ∼ N ( 0 , I ) x_{t_T}^i \sim \mathcal{N}(0, I) xtTi∼N(0,I)。
即便采用少步模型,若对整个自回归扩散过程进行朴素的反向传播,仍会导致过高的内存消耗。为此,我们提出了一种梯度截断策略,将反向传播限制在每一帧的最后一个去噪步骤上。此外,与推理阶段始终使用 T T T 个去噪步骤不同,我们在每次训练迭代中为每个样本序列从区间 [ 1 , T ] [1, T] [1,T] 中随机采样一个去噪步数 s s s,并将第 s s s 步的去噪结果作为最终输出。这种随机采样策略确保了所有中间去噪步骤都能够获得监督信号。我们还通过将梯度流限制在 KV 缓存嵌入中,在训练过程中切断来自先前帧到当前帧的梯度传播。关于完整训练流程的描述,请参见算法 1。

3.3 Holistic Distribution Matching Loss
自回归自展开直接从推理阶段的模型分布中生成样本,使我们能够施加整体性的、视频层面的损失,从而将生成视频的分布 p θ ( x 1 : N ) p_\theta(x^{1:N}) pθ(x1:N) 与真实视频的分布 p data ( x 1 : N ) p_{\text{data}}(x^{1:N}) pdata(x1:N) 对齐。为了利用预训练的扩散模型并提升训练稳定性 [32],我们向两种分布中注入噪声,并匹配 p θ , t ( x t 1 : N ) p_{\theta,t}(x_t^{1:N}) pθ,t(xt1:N) 与 p data , t ( x t 1 : N ) p_{\text{data},t}(x_t^{1:N}) pdata,t(xt1:N),其中二者分别表示在施加前向扩散过程之后得到的分布:
p ⋅ , t ( x t 1 : N ) = ∫ q t ∣ 0 ( x t 1 : N ∣ x 1 : N ) p ⋅ ( x 1 : N ) d x 1 : N . p_{\cdot,t}(x_t^{1:N}) = \int q_{t\mid 0}(x_t^{1:N}\mid x^{1:N})\, p_{\cdot}(x^{1:N})\, \mathrm{d}x^{1:N}. p⋅,t(xt1:N)=∫qt∣0(xt1:N∣x1:N)p⋅(x1:N)dx1:N.
我们的框架在一般意义上适用于多种散度度量与分布匹配范式,本文中我们考虑了三种具体方法:
• 分布匹配蒸馏(Distribution Matching Distillation,DMD)[98, 99]:该方法通过利用分布之间的 score 差异来指导梯度更新,从而最小化反向 Kullback--Leibler 散度 E t [ D K L ( p θ , t ∥ p data , t ) ] \mathbb{E}t\!\left[D{\mathrm{KL}}\!\left(p_{\theta,t}\,\|\,p_{\text{data},t}\right)\right] Et[DKL(pθ,t∥pdata,t)]。
• Score Identity Distillation(SiD)[112, 113]:该方法通过 Fisher 散度进行分布匹配,即
E t , p θ , t [ ∥ ∇ log p θ , t − ∇ log p data , t ∥ 2 ] . \mathbb{E}{t,p{\theta,t}}\!\left[\left\|\nabla \log p_{\theta,t}-\nabla \log p_{\text{data},t}\right\|^2\right]. Et,pθ,t[∥∇logpθ,t−∇logpdata,t∥2].
• 生成对抗网络(GANs)[18]:该方法通过生成器(即我们的自回归扩散模型)与判别器之间的极小极大博弈,近似最小化 Jensen--Shannon 散度,判别器用于区分真实视频与生成视频。
需要强调的是,我们的训练目标在整体层面上将完整视频序列的分布与数据分布进行匹配,即
D ( p data ( x 1 : N ) ∥ p θ ( x 1 : N ) ) . D\!\left(p_{\text{data}}(x^{1:N})\,\|\,p_\theta(x^{1:N})\right). D(pdata(x1:N)∥pθ(x1:N)).
相比之下,TF/DF 可以被理解为执行逐帧分布匹配:
E { x < i } ∼ p data D K L ( p data ( x i ∣ x < i ) ∥ p θ ( x i ∣ x < i ) ) , \mathbb{E}{\{x^{< i}\}\sim p{\text{data}}} D_{\mathrm{KL}}\!\left(p_{\text{data}}(x^i\mid x^{< i})\,\|\,p_\theta(x^i\mid x^{< i})\right), E{x<i}∼pdataDKL(pdata(xi∣x<i)∥pθ(xi∣x<i)),
其中 DF 还会从带噪的数据分布 { x < i } ∼ p ~ data \{x^{< i}\}\sim \tilde{p}{\text{data}} {x<i}∼p~data 中采样上下文帧。我们的建模方式从根本上改变了训练动态------上下文帧 { x < i } \{x^{< i}\} {x<i} 并非来自数据分布(无论是干净的还是带噪的),而是采样自模型自身的分布 p θ p\theta pθ。这种训练分布与推理分布之间的一致性有效缓解了曝光偏置问题,并迫使模型从自身的不完美预测中学习,从而增强其对误差累积的鲁棒性。
尽管上述三种目标均曾用于扩散模型的时间步蒸馏场景中,但我们的核心动机与蒸馏方法有着本质区别:我们旨在通过分布匹配来提升自回归视频生成的质量,以解决曝光偏置问题,而非仅仅加速采样过程。正因如此,其他一些流行的蒸馏方法 [74] 并不适用于我们的框架,因为它们仅关注时间步的缩减,而未直接对齐生成器的输出分布。尽管 CausVid [100] 同样使用 DMD 来匹配生成视频的分布,但其在训练过程中所优化的分布(基于 Diffusion Forcing 的输出)偏离了真实的推理阶段分布,从而显著削弱了其有效性。
3.4 Long Video Generation with Rolling KV Cache
自回归模型相较于标准视频扩散模型的一个关键优势在于其外推能力,原则上可以通过滑动窗口推理生成无限长的视频。尽管使用 Diffusion Forcing 训练的双向注意力模型 [10, 73] 也能够以自回归方式生成视频,但它们不支持 KV 缓存,因此在生成每一个新帧时都需要完整地重新计算注意力矩阵。这会导致过高的计算复杂度 O ( T L 2 ) O(TL^2) O(TL2)(其中 T T T 表示去噪步数, L L L 表示窗口大小),如图 3(a) 所示。
相比之下,采用因果注意力的模型可以利用 KV 缓存来提升效率。然而,现有实现 [69, 100] 仍然需要在相邻滑动窗口之间,对重叠帧重新计算 KV 缓存,如图 3(b) 所示。这在采用密集滑动窗口时会带来 O ( L 2 + T L ) O(L^2 + TL) O(L2+TL) 的计算复杂度。因此,先前方法通常采用较大的步幅并尽量减少窗口重叠以降低计算开销,但这会牺牲时间一致性,因为每个窗口起始处的帧只能依赖显著减少的历史上下文。
受大型语言模型相关研究 [92] 的启发,我们为自回归扩散模型提出了一种滚动式 KV 缓存机制,使其无需重新计算 KV 缓存即可生成无限长的视频。如图 3© 所示,我们维护一个固定大小的 KV 缓存,用于存储最近 L L L 帧中标记的 KV 嵌入。在生成新帧时,我们首先检查 KV 缓存是否已满;若已满,则在加入新的 KV 条目之前移除最旧的条目。该方法在保持生成每一帧时具有足够上下文长度的同时,实现了 O ( T L ) O(TL) O(TL) 的时间复杂度,从而支持无穷帧的连续生成。算法 2 给出了基于滚动 KV 缓存的自回归长视频生成算法的详细描述。
然而,该机制的朴素实现会由于分布不匹配而导致严重的闪烁伪影。具体而言,第一个潜在帧在统计性质上与其他帧不同:它仅对第一张图像进行编码,而未执行时间压缩。模型在训练过程中始终将第一帧视为图像潜变量,因此当在滚动 KV 缓存场景中该图像潜变量不再可见时,模型无法良好泛化。我们的解决方案简单而有效:在训练过程中,我们限制注意力窗口,使模型在对最后一个块进行去噪时无法关注第一个块,从而模拟长视频生成过程中所遇到的条件。
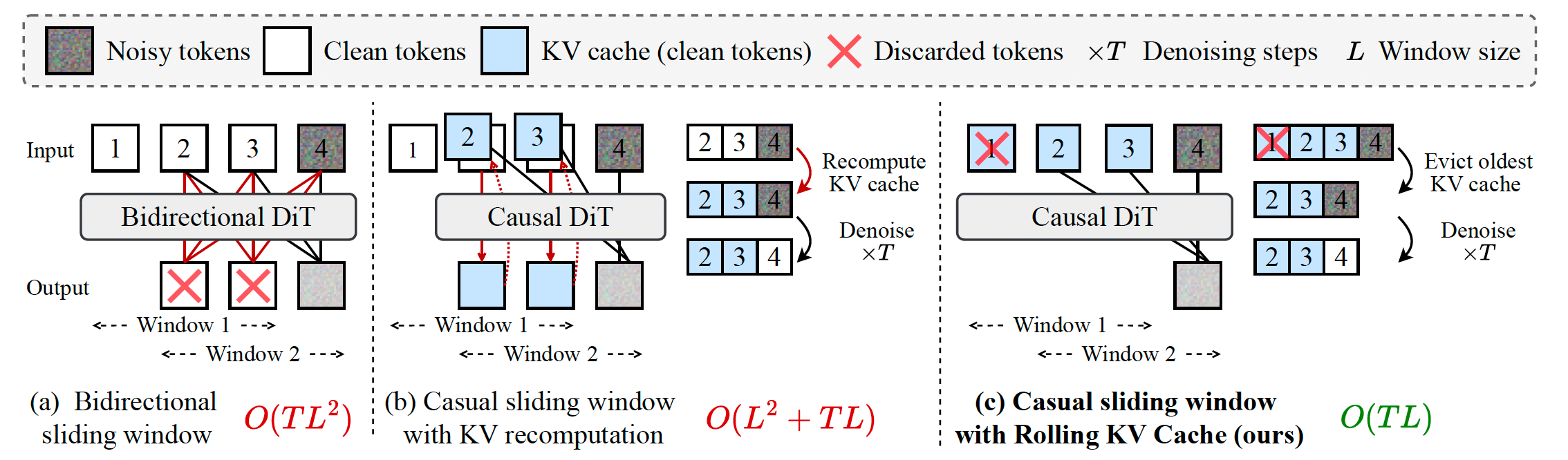
图 3:视频外推的效率对比。在通过滑动窗口推理进行视频外推时,(a) 使用 TF/DF 训练的双向扩散模型 [10, 73] 不支持 KV 缓存。(b) 先前的因果扩散模型 [69, 100] 在窗口移动时需要重新计算 KV。© 我们的方法无需重新计算 KV,从而实现了更高效的外推。