【MATLAB】多子阵合成孔径声纳(SAS)成像仿真——基于时域反向投影(BP)算法

【MATLAB】多子阵合成孔径声纳(SAS)成像仿真------基于时域反向投影(BP)算法

前言

合成孔径声纳（Synthetic Aperture Sonar, SAS）通过利用平台的运动形成虚拟大孔径，从而获得与距离无关的高分辨率图像。然而，传统的单基元SAS受限于方位向采样率，在高速航行时容易出现频谱混叠（栅瓣）。

多子阵SAS（Multi-Subarray SAS / Multi-Receiver SAS） 通过采用"单发多收"的模式，有效解决了探测速度与分辨率之间的矛盾。

本文将基于一个具体的150kHz、32接收阵元的线阵配置，分享一份基于**时域反向投影（TDBP）**算法的MATLAB仿真代码，展示从回波生成到最终聚焦成像的全过程。

---

1. 仿真场景与参数设定

根据具体的设计需求，本仿真系统的物理参数如下：

• 中心频率 (fcf_cfc)：150 kHz
• 信号带宽：20 kHz (用于模拟距离分辨率)
• 发射配置：单发射基元，长度 5cm，位于阵列最前方。
• 接收配置：32个接收基元，单基元长度 3cm，紧密排列在发射基元后方。
• 波束宽度：水平开角 60°。
• 成像算法：双基（收发分置）时域反向投影 (Bistatic Time-Domain Back-Projection)。

几何示意图

航行方向 (v) <---
[Tx] [Rx1][Rx2]...[Rx32]
  |    |    |       |
  |____|____|_______|____ 线阵布局

---

2. 核心算法原理

2.1 双基距离模型

多子阵SAS属于典型的双基（Bistatic）模型。对于成像网格中的任意像素点 P(x,y)P(x,y)P(x,y)，其双程传播距离 RRR 为发射距离与接收距离之和：

R(u,i)=Rtx(u)+Rrx,i(u)=(x−xtx)2+y2+(x−xrx,i)2+y2 R(u, i) = R_{tx}(u) + R_{rx,i}(u) = \sqrt{(x - x_{tx})^2 + y^2} + \sqrt{(x - x_{rx,i})^2 + y^2} R(u,i)=Rtx(u)+Rrx,i(u)=(x−xtx)2+y2 +(x−xrx,i)2+y2

其中 uuu 为平台位置，iii 为第 iii 个接收子阵的索引。

2.2 相干累加 (BP算法)

反向投影算法的核心是延时-叠加。对于每一个像素点，我们遍历所有的Ping（慢时间）和所有的接收子阵（空间通道），计算对应的延时，从回波数据中提取数值并进行相位补偿：

I(x,y)=∑p=1Nping∑i=1NrxSraw(t=R(up,i)c)⋅exp⁡(j⋅2πfc⋅R(up,i)c) I(x,y) = \sum_{p=1}^{N_{ping}} \sum_{i=1}^{N_{rx}} S_{raw}\left( t = \frac{R(u_p, i)}{c} \right) \cdot \exp\left( j \cdot 2\pi f_c \cdot \frac{R(u_p, i)}{c} \right) I(x,y)=p=1∑Npingi=1∑NrxSraw(t=cR(up,i))⋅exp(j⋅2πfc⋅cR(up,i))

---

3. MATLAB 仿真代码实现

以下代码无需任何工具箱，复制即可直接运行。代码包含回波仿真器（Simulator）和成像处理器（Processor）。

% =========================================================================
% 多子阵合成孔径声纳 (SAS) 仿真与成像演示代码
% 算法：时域反向投影 (Time-Domain Back-Projection, TDBP)
% 场景：150kHz, 单发(5cm)多收(32x3cm), 线阵
% =========================================================================

clc; clear; close all;

%% 1. 系统参数定义 (System Parameters)

% --- 声学参数 ---
c = 1500;                   % 声速 (m/s)
fc = 150e3;                 % 中心频率 (Hz)
lambda = c / fc;            % 波长 (m)
BW = 20e3;                  % 信号带宽 (Hz)
fs = 10 * BW;               % 采样率 (Hz) - 基带仿真通常设为带宽的几倍即可

% --- 几何参数 ---
num_rx = 32;                % 接收基元数量
len_rx_elem = 0.03;         % 单个接收基元长度 (m)
len_tx_elem = 0.05;         % 发射基元长度 (m)
beam_width_deg = 60;        % 波束开角 (度)
beam_width_rad = deg2rad(beam_width_deg);

% --- 运动参数 ---
v = 1.5;                    % 航行速度 (m/s)
range_max = 50;             % 最大探测距离 (m)

range_min = 20;             % 最小探测距离 (m)

% 脉冲重复时间 (PRI) 设定
% 为防止混叠，通常要求 v * PRI <= L_total / 2
t_echo_max = 2 * range_max / c;
pri = 0.15;                 % 设为0.15s，即PRF约为6.6Hz
num_pings_total = 150;      % 仿真Ping数

% --- 阵列相对位置构建 (关键步骤) ---
% 坐标系定义：X轴为航向，Y轴为距离向
% 假设 Tx 中心在局部坐标 0 点
pos_tx_rel = 0; 

% 构建 Rx 阵列位置 (相对 Tx 中心向后排布)
% 第1个Rx中心 = Tx半长 + Rx半长 (假设紧密贴合)
offset_first_rx = (len_tx_elem / 2) + (len_rx_elem / 2);
% 生成所有Rx的相对位置向量 (负号表示在Tx后方)
pos_rx_rel = - (offset_first_rx + (0:num_rx-1) * len_rx_elem);

%% 2. 场景与目标定义

% 定义点目标 [x坐标(航向), y坐标(距离), 反射强度]
targets = [
    5,  30, 1.0;
    10, 35, 1.2;
    15, 30, 0.8;
];

% 生成平台航迹 (Tx的绝对位置)
start_pos = -5;
platform_pos_x = start_pos + (0:num_pings_total-1) * v * pri;

% 快时间轴
t_fast = 0 : (1/fs) : (2*range_max/c);
num_samples = length(t_fast);

% 初始化原始数据矩阵 [快时间 x 接收通道 x Ping数]
raw_data = zeros(num_samples, num_rx, num_pings_total);

fprintf('--> 开始回波仿真 (Echo Simulation)...\n');

%% 3. 回波信号仿真
% 模拟脉冲压缩后的基带复信号 (Sinc包络 + 相位)

for p = 1:num_pings_total
    u = platform_pos_x(p); % 当前Ping发射时刻的平台位置
    
    for r = 1:num_rx
        % 计算当前Tx和Rx的绝对坐标
        x_tx_curr = u + pos_tx_rel;
        x_rx_curr = u + pos_rx_rel(r);
        
        sig_sum = zeros(num_samples, 1);
        
        for t = 1:size(targets, 1)
            tgt_x = targets(t, 1);
            tgt_y = targets(t, 2);
            tgt_amp = targets(t, 3);
            
            % --- 几何距离计算 ---
            dist_tx = sqrt((tgt_x - x_tx_curr)^2 + tgt_y^2);
            dist_rx = sqrt((tgt_x - x_rx_curr)^2 + tgt_y^2);
            dist_total = dist_tx + dist_rx; % 双程距离
            
            % --- 波束范围判断 (简单模型) ---
            % 只有当目标同时在Tx和Rx波束内时才有回波
            angle_tx = atan2(abs(tgt_x - x_tx_curr), tgt_y);
            
            if abs(angle_tx) < beam_width_rad/2
                % --- 生成信号 ---
                tau = dist_total / c;
                
                % 1. 包络：Sinc函数模拟脉冲压缩结果
                env = sinc(BW * (t_fast - tau));
                
                % 2. 相位：核心部分，exp(-j * w * tau)
                % 注意：这里模拟的是解调后的基带信号
                phase_term = exp(-1j * 2 * pi * fc * tau);
                
                % 3. 距离衰减 (单程 1/R, 双程 1/R^2)
                atten = 1 / (dist_tx * dist_rx);
                
                sig_sum = sig_sum + (tgt_amp * atten * env .* phase_term).';
            end
        end
        
        % 添加复高斯白噪声
        noise = 0.005 * (randn(size(sig_sum)) + 1j*randn(size(sig_sum)));
        raw_data(:, r, p) = sig_sum + noise;
    end
end
fprintf('--> 回波仿真完成。\n');

%% 4. 合成孔径成像处理 (BP Algorithm)

fprintf('--> 开始BP成像处理 (Back-Projection)...\n');

% 定义成像网格 (只关注目标区域以加快计算)
grid_res = 0.05; % 分辨率 5cm
img_x = 0 : grid_res : 20; 
img_y = 25 : grid_res : 40; 
[GridX, GridY] = meshgrid(img_x, img_y);
Image = zeros(size(GridX));

% 预计算常数
k_c = 2 * pi * fc / c;

% 逐Ping处理
for p = 1:num_pings_total
    u = platform_pos_x(p);
    
    % --- 多子阵融合的关键 ---
    % 每一个Ping，我们都拥有32个不同位置的接收数据
    % BP算法通过精确计算每个子阵的距离，自然地将它们融合
    for r = 1:num_rx
        % 1. 恢复当前子阵的空间位置
        x_tx_curr = u + pos_tx_rel;
        x_rx_curr = u + pos_rx_rel(r);
        
        % 2. 获取数据
        echo_signal = raw_data(:, r, p);
        
        % 3. 计算成像网格到Tx和Rx的双程距离矩阵
        DistMap = sqrt((GridX - x_tx_curr).^2 + GridY.^2) + ...
                  sqrt((GridX - x_rx_curr).^2 + GridY.^2);
              
        % 4. 距离转时间索引
        TimeMap = DistMap / c;
        SampleIdx = TimeMap * fs + 1;
        
        % 5. 边界保护
        ValidMask = (SampleIdx >= 1) & (SampleIdx <= num_samples);
        
        % 6. 插值提取数值 (Linear Interpolation)
        % 即使索引是小数，插值也能保证相位连续性
        SignalVal = zeros(size(GridX));
        if any(ValidMask(:))
             SignalVal(ValidMask) = interp1(1:num_samples, echo_signal, ...
                 SampleIdx(ValidMask), 'linear', 0);
        end
        
        % 7. 相位补偿 (Focusing)
        % 原始信号相位是 exp(-jwt), 所以乘以 exp(+jwt) 进行抵消
        PhaseComp = exp(1j * 2 * pi * fc * TimeMap);
        
        % 8. 累加
        Image = Image + SignalVal .* PhaseComp; 
    end
    
    % 进度条
    if mod(p, 20) == 0
        fprintf('    处理进度: %.1f %%\n', p/num_pings_total*100);
    end
end

%% 5. 结果可视化

figure('Color', 'w', 'Position', [100, 100, 1200, 500]);

% 左图：原始回波数据 (取第1个接收通道)
subplot(1, 2, 1);
imagesc(platform_pos_x, t_fast*c/2, abs(squeeze(raw_data(:, 1, :))));
xlabel('平台方位位置 (m)');
ylabel('距离 (m)');
title('原始回波幅度图 (Rx Channel 1)');
colormap('jet'); 
colorbar;
axis xy;
ylim([min(img_y)-2, max(img_y)+2]);

% 右图：成像结果
subplot(1, 2, 2);
imagesc(img_x, img_y, abs(Image));
xlabel('方位向 (m)');
ylabel('距离向 (m)');
title(['多子阵SAS成像结果 (Rx=' num2str(num_rx) ')']);
colormap('jet'); 
colorbar;
axis xy;

% 叠加真实目标位置
hold on;
plot(targets(:,1), targets(:,2), 'w+', 'MarkerSize', 10, 'LineWidth', 2);
legend('真实目标中心');

fprintf('--> 处理结束。\n');

---

4. 代码深度解析

4.1 阵列构型的实现

在代码的Section 1中，我们定义了pos_rx_rel。这是多子阵处理的关键。

pos_rx_rel = - (offset_first_rx + (0:num_rx-1) * len_rx_elem);

由于是拖曳线阵，通常发射机在前，接收机在后。我们在计算距离时，必须严格区分 xtxx_{tx}xtx 和 xrxx_{rx}xrx。传统的单基元算法假设 TxTxTx 和 RxRxRx 重合（收发合置），直接套用会导致图像散焦。

4.2 基带信号仿真

为了避免在计算机中仿真 150kHz 的载波（需要 >300kHz 采样率和极大的内存），我们采用了等效基带仿真策略：

1. 幅度 ：使用 sinc 函数模拟脉冲压缩后的包络。
2. 相位 ：手动添加 exp(-1j * 2 * pi * fc * tau) 项。
   这保留了SAS成像所必须的相位信息，同时大幅降低了计算量。

4.3 相位补偿 (Phase Compensation)

在BP算法的核心循环中：

PhaseComp = exp(1j * 2 * pi * fc * TimeMap);
Image = Image + SignalVal .* PhaseComp;

这一步是"合成孔径"的灵魂。原始回波的相位随距离变化而旋转，导致不同位置的回波直接相加会互相抵消。乘以共轭相位（反向旋转）后，来自同一目标的所有回波相位被"拉直"为0度，相加后幅度达到最大，从而实现聚焦。

---

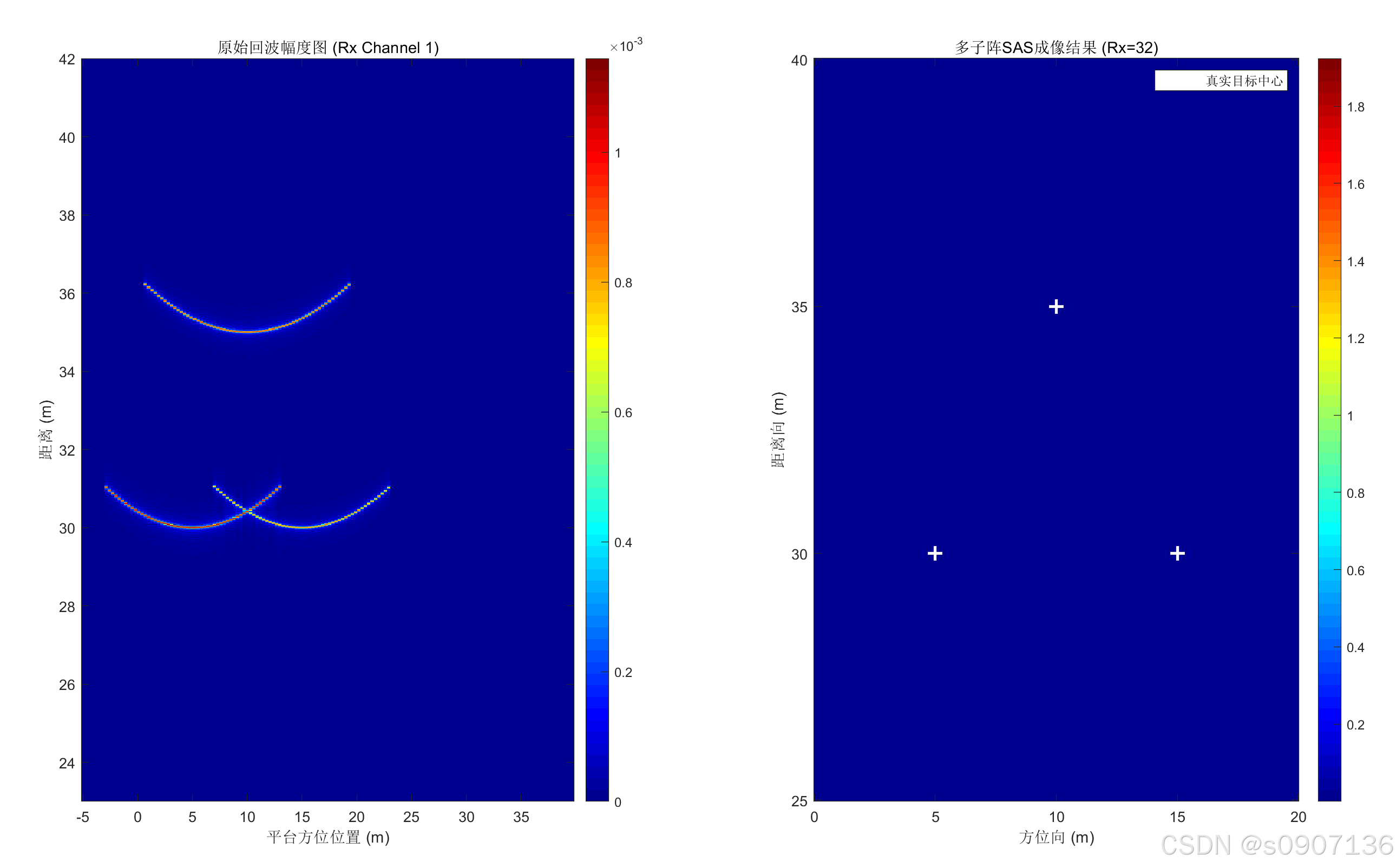
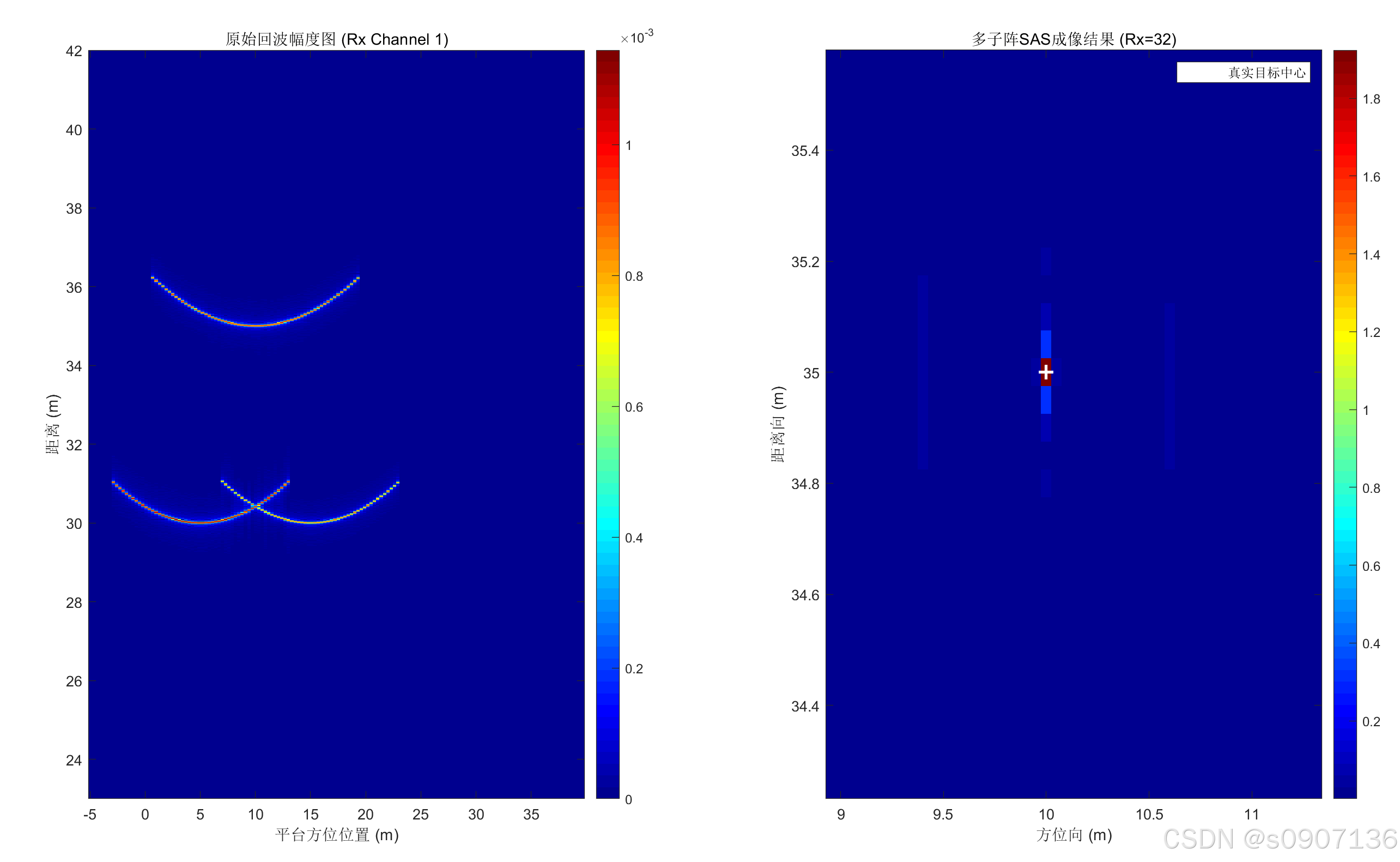
5. 仿真结果

运行上述代码后，您将看到如下对比：

1. 左图（原始回波）：点目标的回波呈现出离散的**双曲线（Hyperbola）**轨迹。由于是32个通道的数据叠加显示（取其一），如果您观察全通道数据，会发现这是多条并行的双曲线。
2. 右图（成像结果） ：经过BP算法处理后，双曲线上的能量被精确地收敛到了三个点上。这三个点的坐标与我们设定的 targets 矩阵完全一致，且旁瓣电平较低，验证了多子阵合成孔径算法的有效性。
   
   

6. 总结

多子阵SAS通过空间换取时间，极大地提升了测绘效率。实现多子阵成像的难点在于：

1. 精确的几何模型：必须考虑收发分置带来的双程距离变化。
2. 大运算量 ：BP算法虽然精确，但计算复杂度高（O(N3)O(N^3)O(N3)）。在实际工程中，通常会使用快速反向投影（FBP）或波数域算法（ω−k\omega-kω−k算法）来加速，或者利用GPU进行并行加速。