彼此之间关系解释:回溯包含在搜索中、而搜索包含在递归中
名词解释
一、递归
1.1、什么是递归?
根据之前所学,可以知道递归实际上就是函数自己调用自己的情况
例如二叉树的遍历,快排、归并
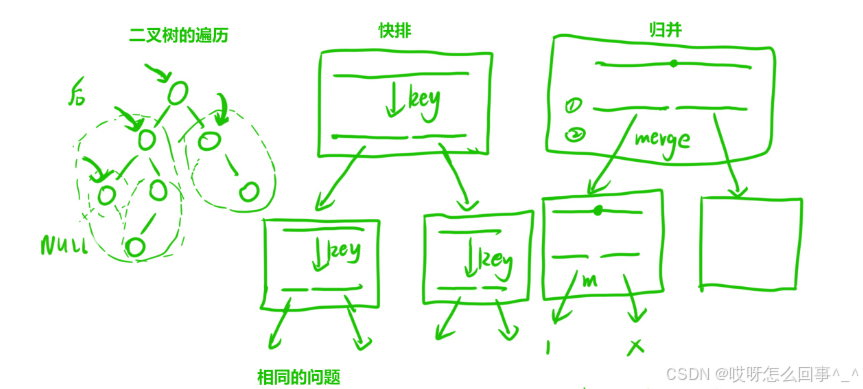
1.2、为什么会用到递归?
这是因为这个问题的解决方式是一个一个子问题的解决方式合起来的,而且这些个子问题的解决方式相同。因此可以用到递归
1.3、如何理解递归?
这个根据自身所学可以分为三个阶段
第一阶段初学,理解递归的方式就是画出递归展开图
第二阶段学到数据结构二叉树时,理解递归不再过度依赖递归展开图
第三阶段就是现在,应该如何理解递归

要去宏观的看待递归,不关心递归展开图。而是先分析递归函数如何写,之后将这个递归函数当作一个黑盒。并且大胆传入递归部分,相信这个黑盒一定能够完成任务
例如二叉树的后序遍历以及归并排序递归写法

将递归函数dfs当作一个黑盒,首先弄清这个函数的作用就是后序遍历此根节点及其下所有子节点,那么处理根节点的左右子树时,就可以将左右子树传入递归函数(当作黑盒),相信其一定可以完成左右子树的后序遍历
归并排序,首先分析子问题就是将每一个区间内数据排序,排序的方式就是先分为两部分将这两部分排为各自有序之后再合起来整体有序。那么每一个区间都可以这样处理,这就是相同的子问题,并且merge函数当作黑盒大胆传入细分之后的区间
1.4、如何写好一个递归
写出某一个子问题的递归函数,将细分的部分在这个函数内调用,也就是自己调用自己之后注意一下递归函数返回条件即可,不能无限递归

二、搜索
2.1、搜索中出现的名词解释
解释在搜索这部分出现的一些名词:宽度优先遍历、宽度优先搜索、深度优先遍历、深度优先搜索、暴搜
宽度优先遍历就是bfs、深度优先遍历就是dfs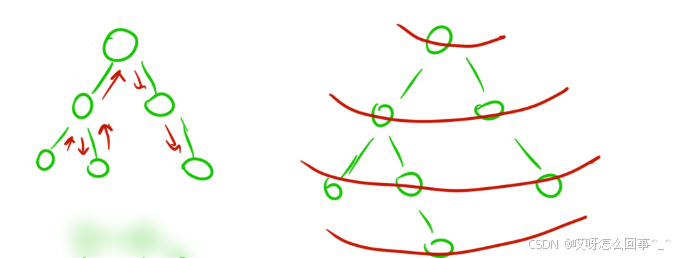
至于深度优先搜索和宽度优先搜索实际上就是在各自遍历中找到某些或者某一个有限个数据;可以说遍历是一种方式,而搜索才是一种目的
暴搜:暴力枚举一遍所有情况,实际上就是bfs和dfs
2.2、搜索扩展------决策树
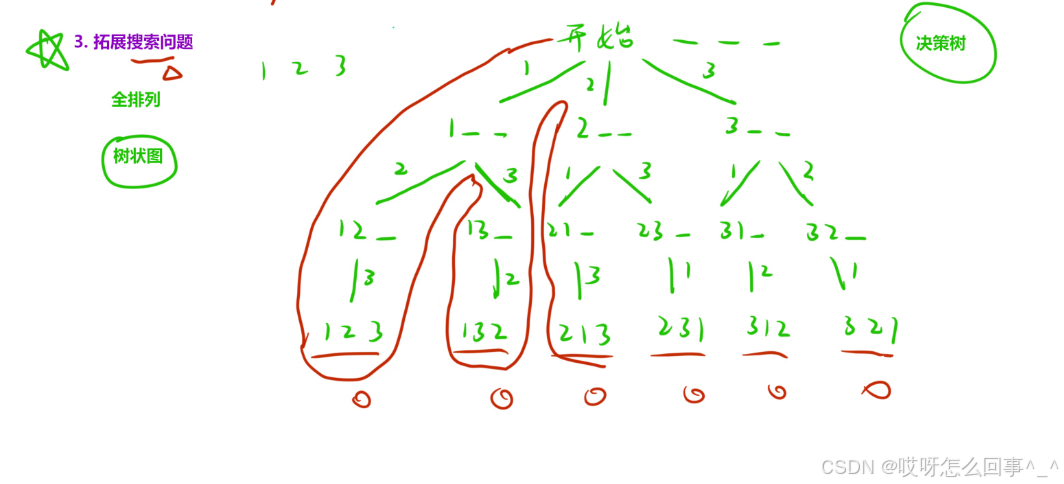
像这种全排列问题,在中学阶段这种图叫树状图,现在叫决策树,在之后的问题中决策树要先画出来,之后根据决策树写递归代码
三、回溯与剪枝
回溯的本质就是深搜
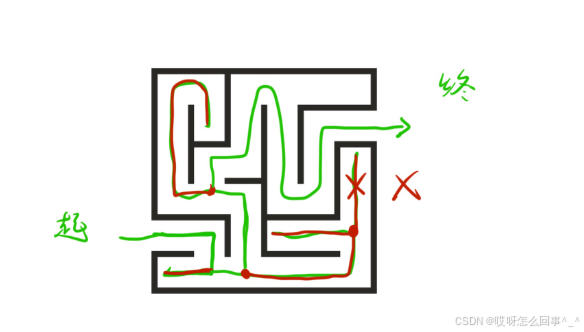
就看这个迷宫问题,找出口。从起点开始深度优先遍历,碰到墙壁不能走了就应回溯到分叉点,所以可以说回溯就是深搜,只有深搜了才会有回溯