【面试手撕】如何构造二叉树输入用例？ACM模式，路径总和2解题思路

程序员三明治2026-01-18 9:17

👨‍💻程序员三明治 ：个人主页
🔥 个人专栏 : 《设计模式精解》 《重学数据结构》

🤞先做到 再看见！

目录

概述

二叉树可以有两种存储方式，一种是 链式存储，另一种是顺序存储。

链式存储，就是大家熟悉的二叉树，用指针指向左右孩子。

顺序存储，就是用一个数组来存二叉树，其方式如图所示：

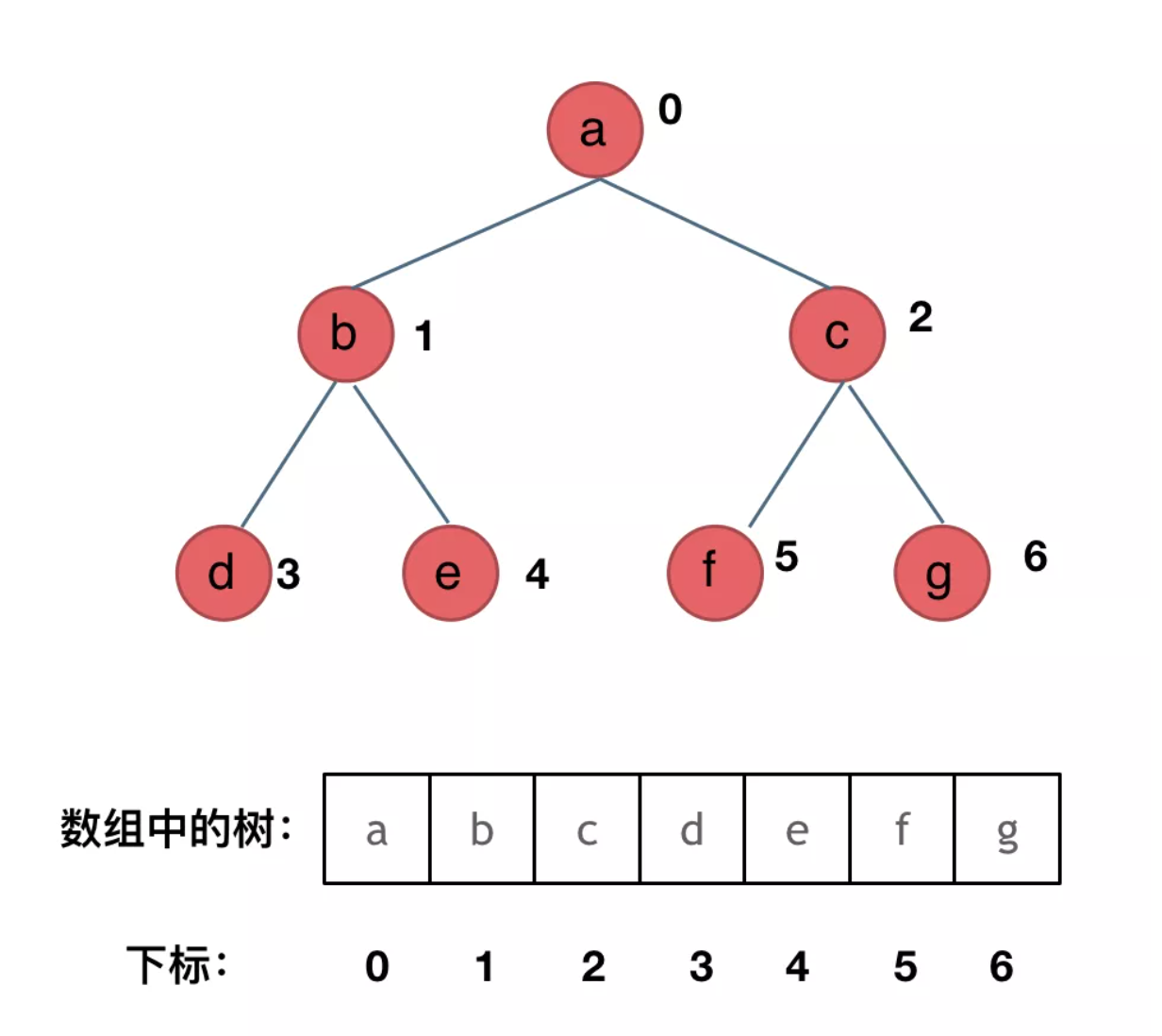
如果父节点的数组下标是i，那么它的左孩子下标就是i * 2 + 1，右孩子下标就是 i * 2 + 2。

思路

定义二叉树类

java 复制代码 
class TreeNode {
    int val;
    TreeNode left, right;
    public TreeNode() {}
    public TreeNode(int val) {
        this.val = val;
    }

}

将二叉树的完全二叉树形式定义为数组

以下图为例：

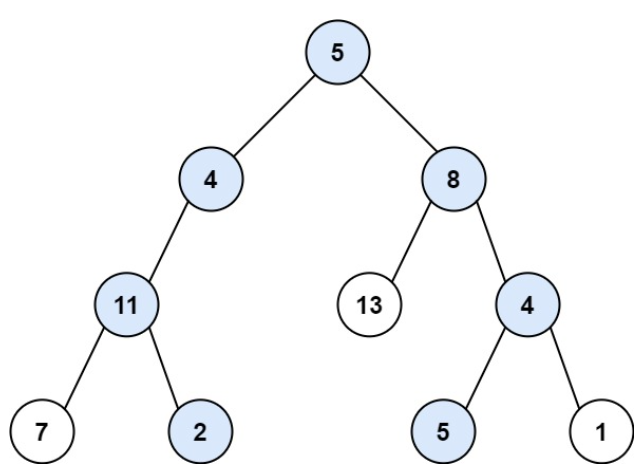
我们可以定义为数组：

java 复制代码 
int[] nums = new int[]{5, 4, 8, 11, -1, 13, 4, 7, 2, -1, -1, -1, -1, 5, 1};

根据数组构造二叉树

buildBinaryTree 的作用是：把一个用数组按层序（堆式下标）表示的二叉树构建成真正的链式二叉树 。其中 -1 用来表示"这个位置没有节点（null）"。

1）整体思路（两趟构建）

这段代码分两步做：

  1. 先把数组每个位置都变成一个 **TreeNode** 或 **null** ，放进 **nodeList**（下标一一对应）
  2. 再按下标规则，把每个非空节点的左/右孩子指针连起来

这样做的好处是：第二步连指针时，孩子节点对象已经准备好了，直接取 nodeList 里的引用即可。

2）第一段循环：创建节点列表 + 确定根节点

java 复制代码 
if (nums.length == 0) return null;
List<TreeNode> nodeList = new ArrayList<>();
TreeNode root = null;

for (int i = 0; i < nums.length; i++) {
    TreeNode node = null;
    if (nums[i] != -1) {
        node = new TreeNode(nums[i]);
    }
    nodeList.add(node);
    if (i == 0) {
        root = node;
    }
}

逐行解释：

  • nums.length == 0：空数组，当然没有树，直接返回 null。
  • nodeList：用来存放所有节点（或 null），并且保证 **nodeList[i]** 对应 **nums[i]** 的位置。
  • TreeNode node = null;：默认这个位置没有节点。
  • if (nums[i] != -1)：如果不是 -1，就创建真实节点 new TreeNode(nums[i])；否则保持 null。
  • nodeList.add(node)：把这个位置的节点（或 null）放进列表。
  • if (i == 0) root = node;：数组的第 0 位代表根节点，所以根就是 nodeList[0]。

注意：如果 nums[0] == -1，那么根就是 null，最终返回空树。

3）第二段循环：按"堆下标规则"连接左右孩子

java 复制代码 
for (int i = 0; i < nums.length; i++) {
    TreeNode node = nodeList.get(i);
    if (node != null) {
        if (i * 2 + 1 < nums.length) {
            node.left = nodeList.get(i * 2 + 1);
        }
        if (i * 2 + 2 < nums.length) {
            node.right = nodeList.get(i * 2 + 2);
        }
    }
}

这里使用的是数组表示完全二叉树的经典下标关系：

  • 对于下标 i 的节点：
    • 左孩子下标：2*i + 1
    • 右孩子下标：2*i + 2

代码关键点：

  • TreeNode node = nodeList.get(i);
    • 取出当前位置的节点引用。
  • if (node != null)：
    • 只有当前节点真实存在，才有必要去给它连孩子；如果本身是空位置（null），就跳过。
  • if (i * 2 + 1 < nums.length) / if (i * 2 + 2 < nums.length)：
    • 防止孩子下标越界。
  • node.left = nodeList.get(2*i + 1)：
    • 直接把列表中对应位置的节点引用挂到 left 上。
    • 如果那个位置是 null，那就等价于"左孩子为空"，完全符合预期。

4）返回结果

java 复制代码 
return root;

root 就是整棵树的入口节点（可能为 null）。

5）一个小例子帮助理解

假设：
nums = [1, 2, 3, -1, 4]

nodeList 会变成：

  • 0: 1
  • 1: 2
  • 2: 3
  • 3: null
  • 4: 4

连接关系：

  • i=0(1)：left=2(i=1)，right=3(i=2)
  • i=1(2)：left=null(i=3)，right=4(i=4)

最终树结构：

plain 复制代码 
    1
   / \
  2   3
   \
    4

核心完整代码

java 复制代码 
    private static TreeNode buildBinaryTree(int[] nums) {
        // 1.把输入数值数组，先转化为二叉树节点列表
        if (nums.length == 0) return null;
        List<TreeNode> nodeList = new ArrayList<>();
        TreeNode root = null;
        for (int i = 0; i < nums.length; i++) {
            TreeNode node = null;
            if (nums[i] != -1) {
                node = new TreeNode(nums[i]);
            }
            nodeList.add(node);
            if (i == 0) {
                root = node;
            }
        }
        // 2.遍历一遍，根据规则给左右孩子赋值就可以了
        for (int i = 0; i < nums.length; i++) {
            TreeNode node = nodeList.get(i);
            if (node != null) {
                if (i * 2 + 1 < nums.length) {
                    node.left = nodeList.get(i * 2 + 1);
                }
                if (i * 2 + 2 < nums.length) {
                    node.right = nodeList.get(i * 2 + 2);
                }
            }
        }
        return root;
    }

下面我们来看一道力扣题，完美应用了二叉树的构造

Leetcode113. 路径总和②

这里使用ACM代码形式去写

题目描述

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。

叶子节点 是指没有子节点的节点。

示例 1：

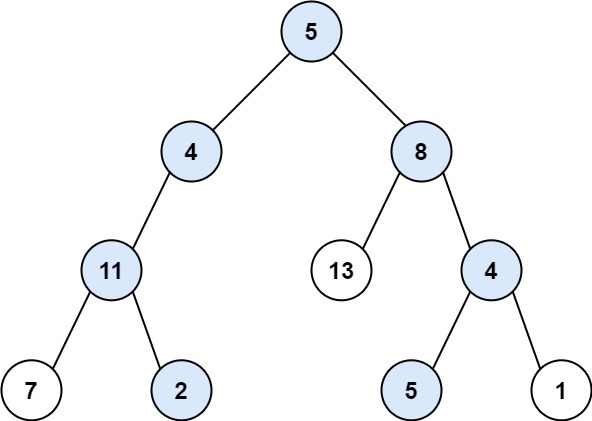
plain 复制代码 
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

思路

毫无疑问，树形递归。递归有两大步：

  1. 确定递归的终止条件、参数
  2. 确定单层递归的逻辑

本题终止条件是遇到叶子结点，判断targetSum是否为0，所以这里需要在进入本次递归之前就把这个节点的值给减掉，并把这个节点提前加入到path中。

单层递归我们用的是先序遍历，根左右。

递推参数： 当前节点 root ，当前目标值 targetSum 。

终止条件： 若节点 root 为空，则直接返回。

递推工作：

路径更新： 将当前节点值 root.val 加入路径 path 。

目标值更新： targetSum = targetSum - root.val（即目标值 targetSum 从 原始的targetSum 减至 0 ）。

路径记录： 当 (1) root 为叶节点 且 (2) 路径和等于目标值 ，则将此路径 path 加入 res 。

先序遍历： 递归左 / 右子节点。

路径恢复： 向上回溯前，需要将当前节点从路径 path 中删除，即执行 path.pop() 。

代码如下：

java 复制代码 
public class PathSum2 {
    static List<Integer> path = new ArrayList<>();
    static List<List<Integer>> res = new ArrayList<>();
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int[] nums = new int[]{5, 4, 8, 11, -1, 13, 4, 7, 2, -1, -1, -1, -1, 5, 1};
        TreeNode root = buildBinaryTree(nums);
        System.out.println("请输出总和数值：");
        int targetSum = scanner.nextInt();
        res = getPathSum2(root, targetSum);
        System.out.println("结果：" + res);
        scanner.close();
    }


    private static List<List<Integer>> getPathSum2(TreeNode root, int targetSum) {
        if (root == null) return res;
        path.add(root.val);
        dfs(root, targetSum - root.val);
        return res;
    }

    private static void dfs(TreeNode root, int targetSum) {
        // 递归的终止条件
        if (root.left == null && root.right == null) {
            if (targetSum == 0) {
                res.add(new ArrayList<>(path));
            }
        }
        // 单层递归的逻辑，根左右
        if (root.left != null) {
            path.add(root.left.val);
            dfs(root.left, targetSum - root.left.val);
            path.remove(path.size() - 1);
        }
        if (root.right != null) {
            path.add(root.right.val);
            dfs(root.right, targetSum - root.right.val);
            path.remove(path.size() - 1);
        }
    }

    // 构造二叉树
    private static TreeNode buildBinaryTree(int[] nums) {
        // 1.把输入数值数组，先转化为二叉树节点列表
        if (nums.length == 0) return null;
        List<TreeNode> nodeList = new ArrayList<>();
        TreeNode root = null;
        for (int i = 0; i < nums.length; i++) {
            TreeNode node = null;
            if (nums[i] != -1) {
                node = new TreeNode(nums[i]);
            }
            nodeList.add(node);
            if (i == 0) {
                root = node;
            }
        }
        // 2.遍历一遍，根据规则给左右孩子赋值就可以了
        for (int i = 0; i < nums.length; i++) {
            TreeNode node = nodeList.get(i);
            if (node != null) {
                if (i * 2 + 1 < nums.length) {
                    node.left = nodeList.get(i * 2 + 1);
                }
                if (i * 2 + 2 < nums.length) {
                    node.right = nodeList.get(i * 2 + 2);
                }
            }
        }
        return root;
    }
}
class TreeNode {
    int val;
    TreeNode left, right;
    public TreeNode() {}
    public TreeNode(int val) {
        this.val = val;
    }

}

【注意事项】

在使用这段代码时，请务必注意以下两点： 空节点的占位：这段代码依赖于数组是 "完整" 的。如果父节点存在但子节点缺失，数组中必须填入 -1占位。如果数组直接跳过了 -1，那么 i * 2 + 1 的数学关系就会失效，导致树构建错误。 数值冲突：代码中硬编码了 -1代表空。如果你的二叉树节点值本身就可能包含 -1，记得把判断条件改成 Integer.MAX_VALUE 或其他不会冲突的特殊值。

好记性不如烂笔头，建议大家把这段代码收藏起来，下次刷 LeetCode 需要自己写测试用例的时候，直接拿来即用！

如果我的内容对你有帮助，请辛苦动动您的手指为我点赞，评论，收藏。感谢大家!!

相关推荐
干前端2 小时前
Message组件和Vue3 进阶：手动挂载组件与 Diff 算法深度解析
javascript·vue.js·算法
ゞ 正在缓冲99%…2 小时前
2025.12.17华为软开
java·算法
子午2 小时前
【2026原创】文本情感识别系统~Python+深度学习+textCNN算法+舆情文本+模型训练
python·深度学习·算法
Flash.kkl2 小时前
递归、搜索与回溯算法概要
数据结构·算法
s09071362 小时前
【MATLAB】多子阵合成孔径声纳(SAS)成像仿真——基于时域反向投影(BP)算法
算法·matlab·bp算法·合成孔径
Xの哲學2 小时前
Linux Workqueue 深度剖析: 从设计哲学到实战应用
linux·服务器·网络·算法·边缘计算
sin_hielo2 小时前
leetcode 3047
数据结构·算法·leetcode
JAI科研2 小时前
MICCAI 2025 IUGC 图像超声关键点检测及超声参数测量挑战赛
人工智能·深度学习·算法·计算机视觉·自然语言处理·视觉检测·transformer
mit6.8242 小时前
思维|状压dp
算法
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）032025年大语言模型技术全景报告04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Claude Code Skills 实用使用手册07UV安装并设置国内源08Labelme从安装到标注：零基础完整指南09AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南10BongoCat - 跨平台键盘猫动画工具