
💡Yupureki:个人主页
🌸Yupureki🌸的简介:

目录
[1. 凌乱的yyy / 线段覆盖](#1. 凌乱的yyy / 线段覆盖)
[2. Radar Installation](#2. Radar Installation)
[3. Sunscreen G](#3. Sunscreen G)
[4. Stall Reservations S](#4. Stall Reservations S)
区间问题
1. 凌乱的yyy / 线段覆盖
题目链接:
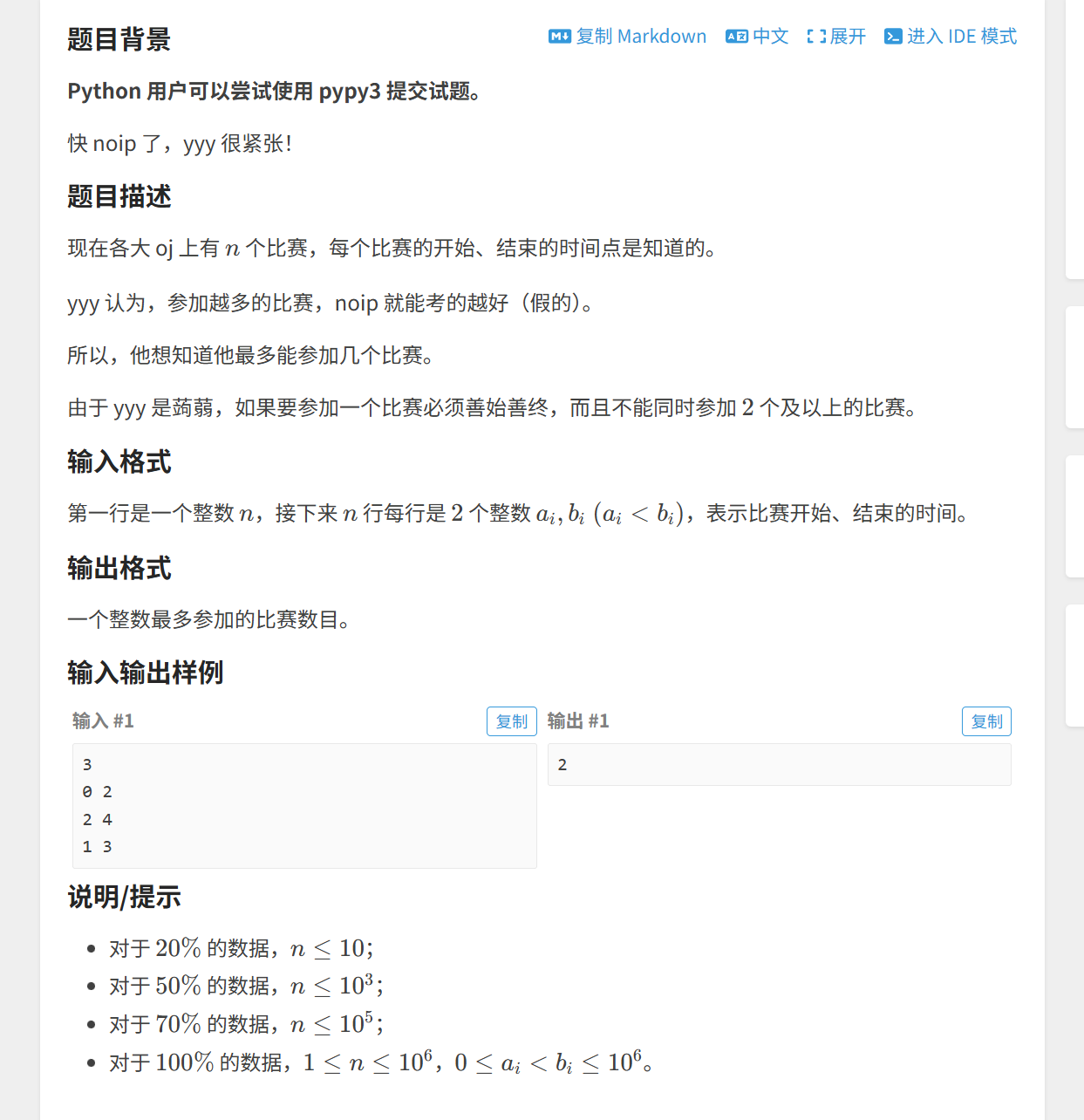
算法原理
贪心思想:
我们先把所有的区间按照左端点从小到大排序
排完序如何选择?
如果两个区间不重合
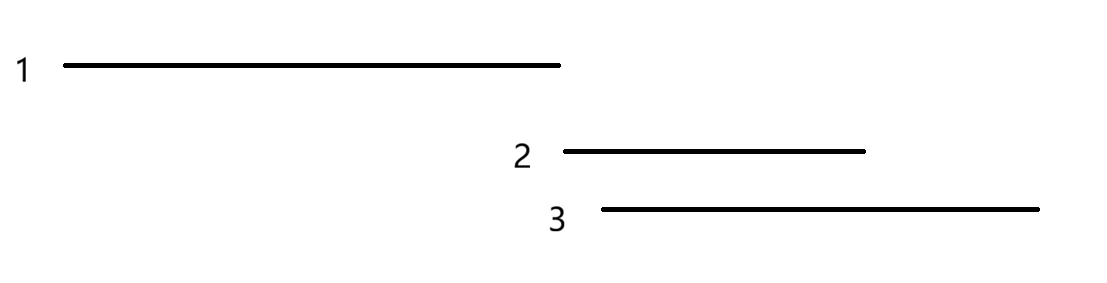
那么我们选择区间1不会影响后续的区间的抉择,相当于是白送一条
如果两个区间重合,有两种情况
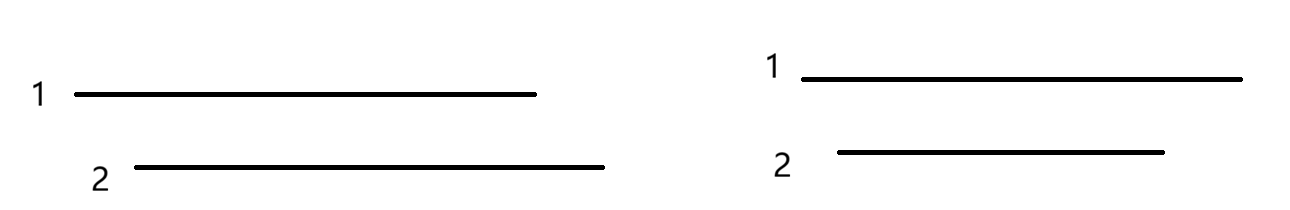
我们排完序后肯定是1的左端点小于2的左端点的,那么两种情况无非是1的右端点大于或者小于2的右端点
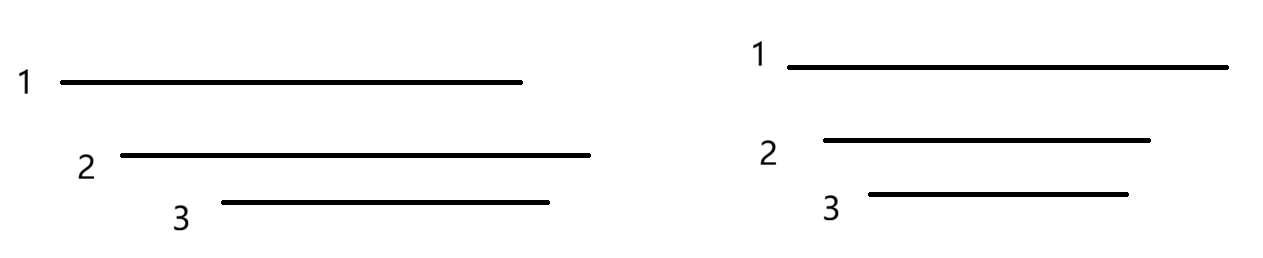
假设3都被2和1"包裹着",那么选择1和2都不能选3,似乎都可以
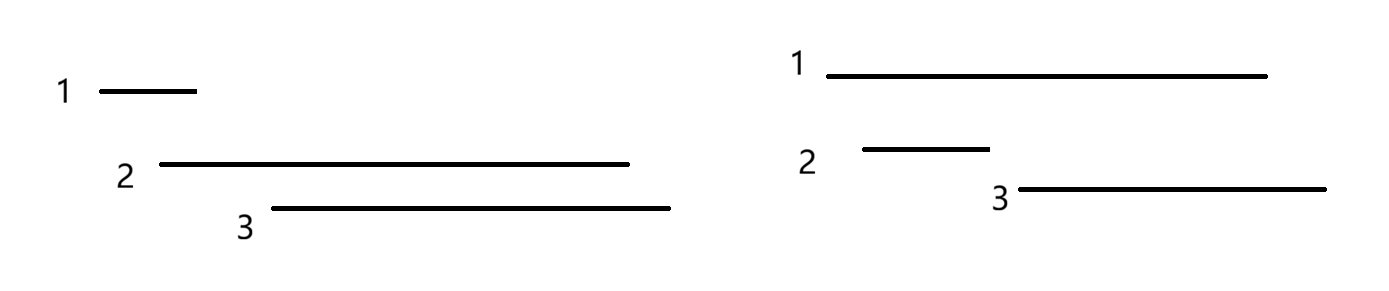
但是假设3的左端点大于1或者2的右端点,我们发现左边选择1也可以选择3,右边选择2也可以选择3
因此我们大胆断定,对于两条区间,我们选择右端点较小的那个是最优解
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
bool cmp(const pair<int,int>& x,const pair<int,int>& y)
{
return x.first < y.first;
}
int main()
{
vector<pair<int, int>> v;
int n; cin >> n;
while (n--)
{
int l, r; cin >> l >> r;
v.push_back({ l,r });
}
sort(v.begin(),v.end(),cmp);
int ret = 0;
int r = v[0].second;
for (int i = 1; i < v.size(); i++)
{
int l = v[i].first;
int r2 = v[i].second;
if (r <= l)
{
r = r2;
ret++;
}
else if (r2 < r)
{
r = r2;
}
}
cout << ret + 1;
return 0;
}2. Radar Installation
题目链接:

算法原理
贪心思想:
由图可知,当一个岛屿的坐标确定时,我们可以计算出,哪段区间可以使雷达覆盖这个岛屿
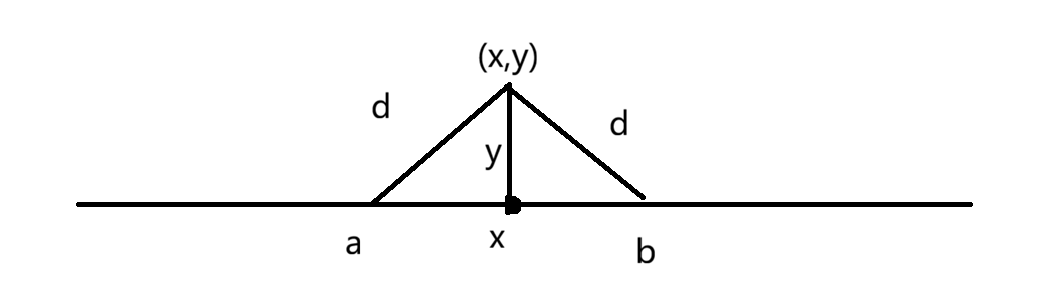
因此我们可以预处理出一个岛屿映射在x轴上的有效雷达区间
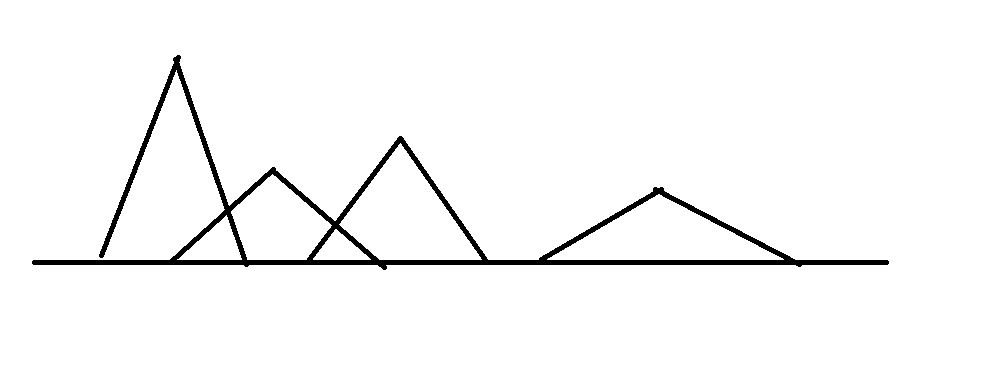
之后将这些区间按照左端点从小到大排序,对于重合的两个区间,选择较小的右端点即可
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>
using namespace std;
bool cmp(const pair<double, double>& x, const pair<double, double>& y)
{
return x.second < y.second;
}
int main()
{
int num = 1;
int n, m;
while (1)
{
cin >> n >> m;
if (n == 0 && m == 0)
break;
vector<pair<double, double>> v;
int check = 0;
for (int i = 0; i < n; i++)
{
int x, y; cin >> x >> y;
if (y > m)
{
check = 1;
v.push_back({ 0,0 });
continue;
}
double l = x - sqrt(m * m - y * y);
double r = x + sqrt(m * m - y * y);
v.push_back({ l,r });
}
if (check)
{
cout << "Case " << num << ": -1" << endl;
num++;
continue;
}
sort(v.begin(), v.end(), cmp);
int ret = 0;
double r = v[0].second;
for (int i = 1; i < v.size(); i++)
{
if (v[i].first > r)
{
ret++;
r = v[i].second;
}
}
cout << "Case " << num << ": " << ret + 1 << endl;
num++;
}
return 0;
}3. Sunscreen G
题目链接:

算法原理
我们参考之前的做法,可以发现有多种排序和选择的方法
- 左端点从大到小 + 防晒霜从大到小
- 左端点从小到大 + 防晒霜从大到小
- 左端点从大到小 + 防晒霜从小到大
- 左端点从小到大 + 防晒霜从小到大
- 右端点从大到小 + 防晒霜从大到小
- 右端点从小到大 + 防晒霜从大到小
- 右端点从大到小 + 防晒霜从小到大
- 右端点从小到大 + 防晒霜从小到大
但实际上很多选法是错误的
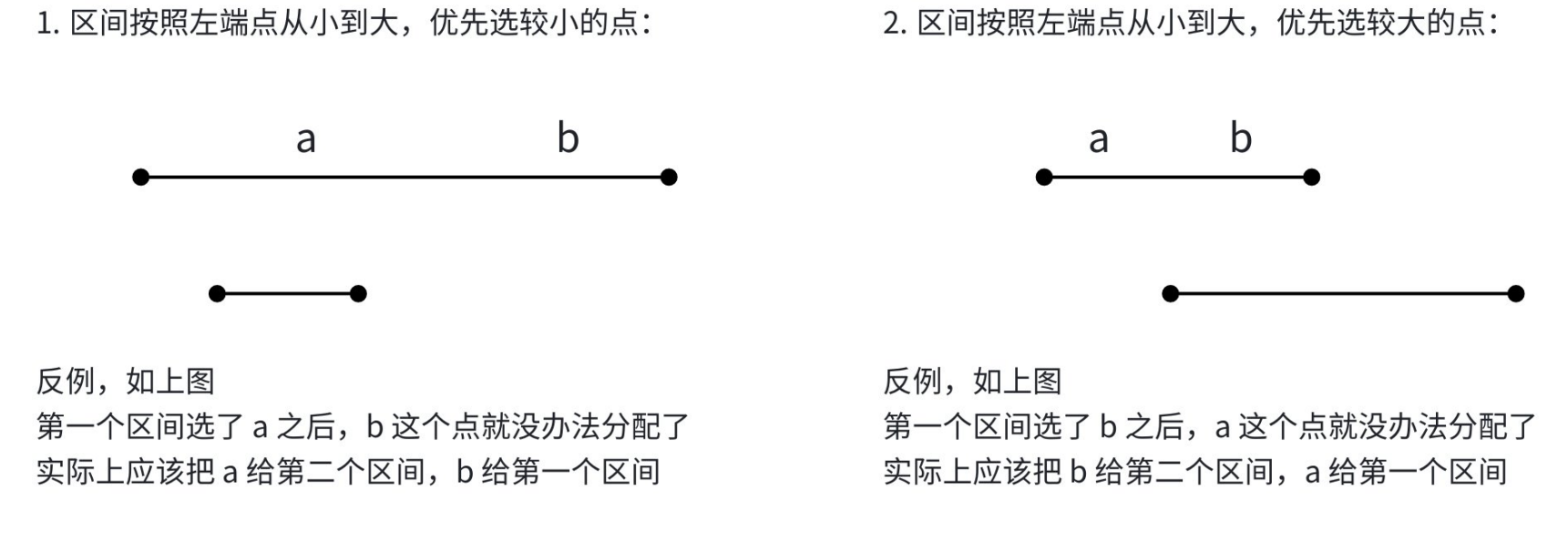
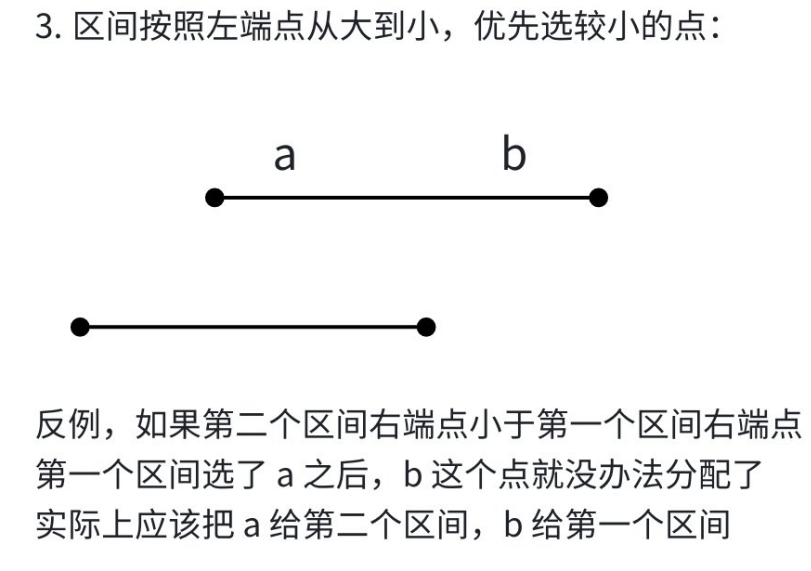
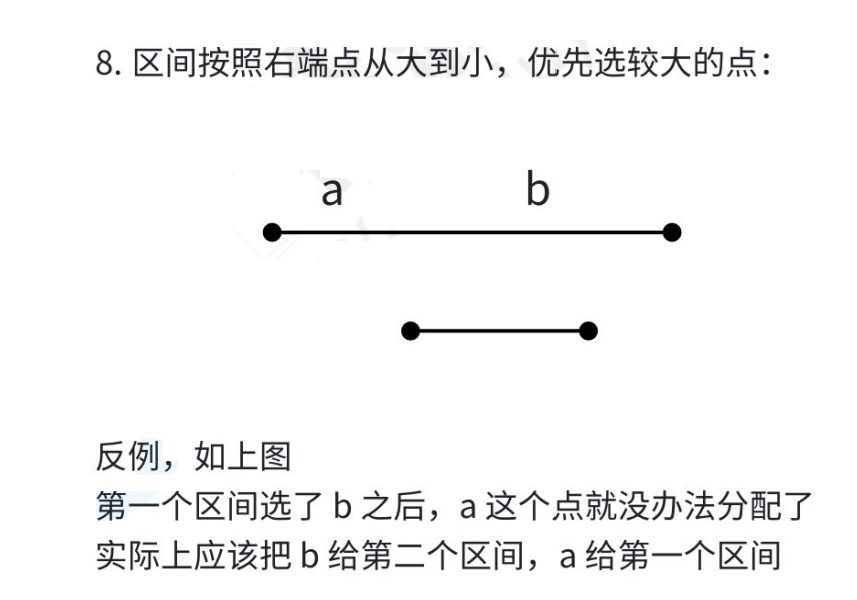
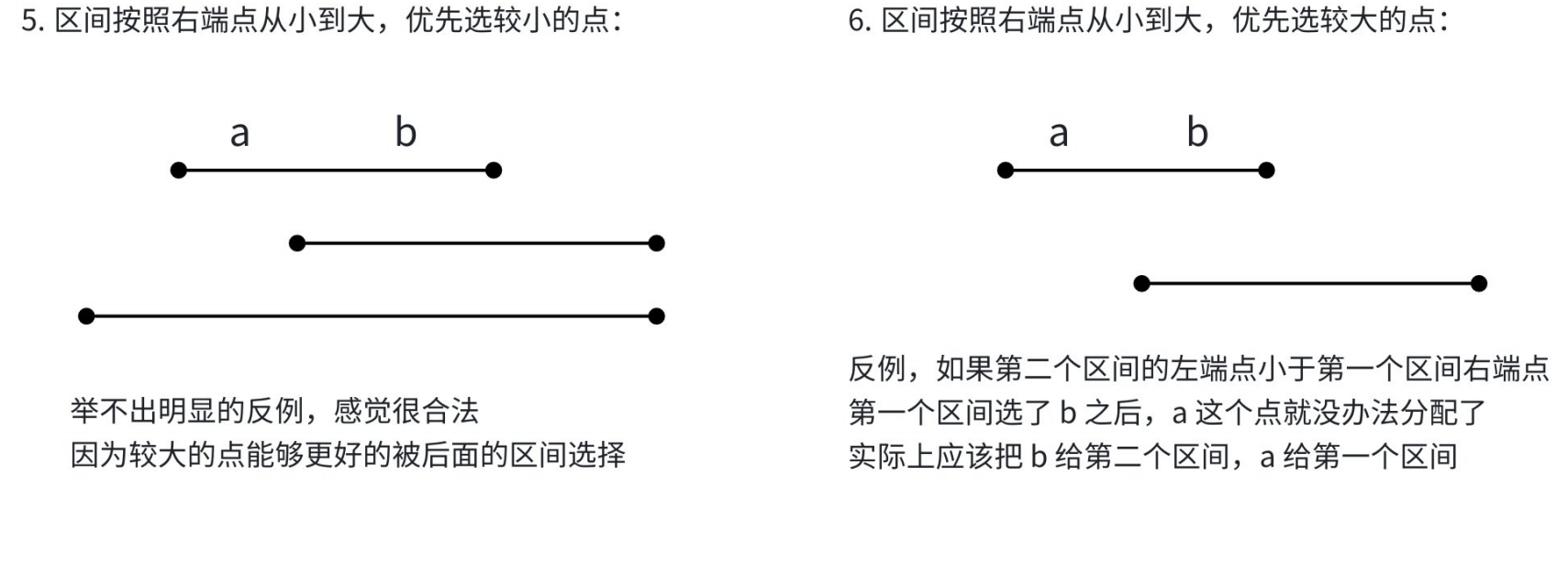
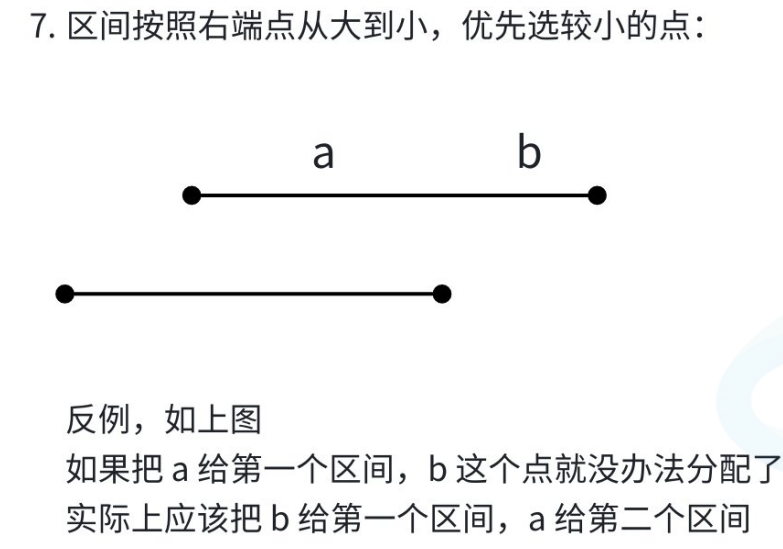
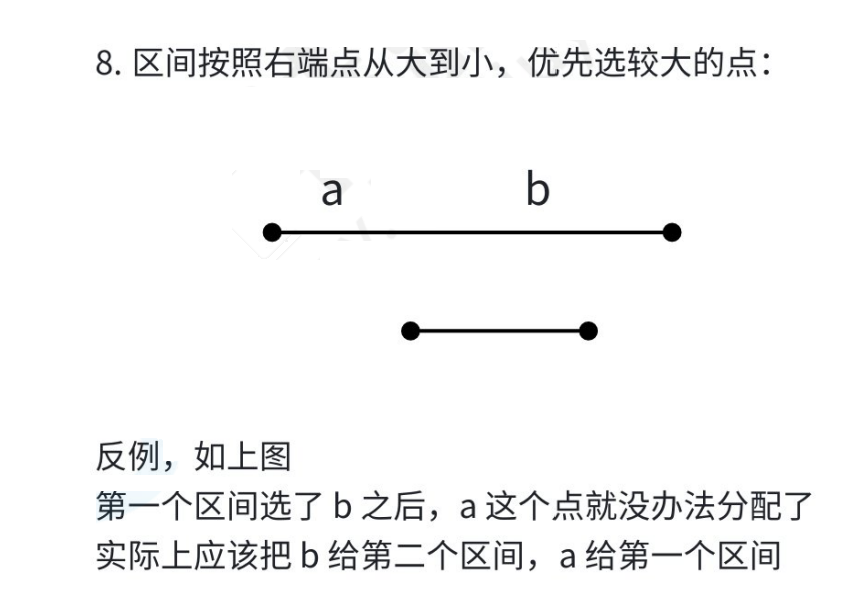
综合分析,有两种情况是正确的
-
左端点从大到小 防晒霜从大到小 选择较大的防晒霜
-
右端点从小到大 防晒霜从小到大 选择较小的防晒霜
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
bool cmp(const pair<int, int>& x, const pair<int, int>& y)
{
return x.first > y.first;
}
int main()
{
int n, m; cin >> n >> m;
vector<pair<int, int>> C;
vector<pair<int, int>> L;
for (int i = 0; i < n; i++)
{
int l, r; cin >> l >> r;
C.push_back({ l,r });
}
for (int i = 0; i < m; i++)
{
int a, b; cin >> a >> b;
L.push_back({ a,b });
}
sort(C.begin(), C.end(), cmp);
sort(L.begin(), L.end(), cmp);
int ret = 0;
for (int i = 0; i < C.size(); i++)
{
int l = C[i].first; int r = C[i].second;
for (int j = 0; j < L.size(); j++)
{
int w = L[j].first;
int& count = L[j].second;
if (w > r || count == 0)continue;
if (w < l)break;
count--;
ret++;
break;
}
}
cout << ret;
return 0;
}4. Stall Reservations S
题目链接:

算法原理
贪心思想:
按照「起始时间」对所有奶牛「从小到大」排序,然后「从前往后」依次安排每一头奶牛,设这头奶牛的产奶的时间区间是[a,b]:
在已经有牛的所有牛棚里,如果「结束时间小于a」,就可以把这头奶牛放在这个牛棚里面;如果
有很多符合要求的,我们应该找一个「结束时间最大」的,这样可以将「结束时间较小」的留在后
面,为后面的区间提供更多的机会。
如果所有已经有牛的牛棚的「结束时间都大于」,那么这头牛只能自己单独开一个牛棚。
代码如何实现?
第一步:预处理
- 读入所有区间,同时记录原始编号(因为后面要排序)
- 按开始时间排序,开始时间相同则按结束时间排序
第二步:贪心分配
- 初始化一个最小堆,存储
(结束时间, 牛棚编号) - 遍历每个区间(按排序后的顺序):
- 情况A :堆顶的结束时间 < 当前区间开始时间
- 说明该牛棚已空闲,可以复用
- 弹出堆顶,将该牛棚分配给当前区间,更新结束时间后重新入堆
- 情况B :堆空 或 堆顶结束时间 ≥ 当前区间开始时间
- 说明没有空闲牛棚,需要新建
- 分配新牛棚编号,将其结束时间入堆
- 情况A :堆顶的结束时间 < 当前区间开始时间
实操代码
cpp
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#include <functional>
using namespace std;
struct Cow {
int start, end, id;
};
bool cmp(const Cow &a, const Cow &b)
{
if (a.start == b.start) return a.end < b.end;
return a.start < b.start;
}
int main()
{
int N;
cin >> N;
vector<Cow> cows(N);
for (int i = 0; i < N; ++i)
{
cin >> cows[i].start >> cows[i].end;
cows[i].id = i;
}
sort(cows.begin(), cows.end(), cmp);
// 最小堆:(结束时间, 牛棚编号)
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
vector<int> ans(N);
int next_id = 1;
for (const Cow &cow : cows)
{
if (!pq.empty() && pq.top().first < cow.start)
{
// 复用牛棚
int stall_id = pq.top().second;
pq.pop();
pq.push({cow.end, stall_id});
ans[cow.id] = stall_id;
} else
{
// 新建牛棚
ans[cow.id] = next_id;
pq.push({cow.end, next_id});
next_id++;
}
}
int ret = next_id - 1;
cout << ret << "\n";
for (int i = 0; i < N; ++i) {
cout << ans[i] << "\n";
}
return 0;
}