【神经网络的训练策略选取】

NN的训练策略选取

1、采用随机梯度下降替代其他梯度下降方法

(1) 不用每输入一个样本就去变换参数，而是输入一批样本（batch），求出这些样本梯度的均值，根据均值改变参数。

(2) 在神经网络训练中，batch的样本数大致50-200不等。

这里准确来说是采用小批量的一个随机梯度下降（mini-batch SGD）方法，详细的各种梯度下降策略和梯度下降是什么，详见 线性回归 这篇博客，这里就不做赘述，这里讲一下BP算法。

1.1 BP算法（Back Propagation）

BP算法，中文翻译为反向传播算法，它是神经网络求出各神经元参数最核心的思想，神经网络通过反向传播梯度下降，更新参数，寻找最优解。Hinton 和他的团队在 1986 年通过论文《Learning representations by backpropagating errors》重新提出并推广了反向传播算法，使得神经网络能够高效地训练多层网络，突破了神经网络发展的瓶颈，推动了深度学习的兴起。Hinton是深度学习的开创者之一，有幸查过他的简历，每次看都会感慨，大佬就是大佬，由心理学跨越到计算机科学，还能有开创性的研究成果。

BP算法：

梯度下降法求局部极值。

① 找一个 w w w.

② 设 k = 0 k=0 k=0，假设 d f ( w ) d w ∣ w k = 0 \frac{df(w)}{dw}|{w_k=0} dwdf(w)∣wk=0，退出。否则： w k + 1 = w k − α d f ( w ) d w ∣ w k w{k+1}=w_k-\alpha\frac{df(w)}{dw}|w_k wk+1=wk−αdwdf(w)∣wk.

其中， α \alpha α是学习率。

举个具体示例：

1. 随机取 ( w 11 , w 12 , w 21 , w 22 , b 1 , b 2 , w 1 , w 2 , b ) (w_{11},w_{12},w_{21},w_{22},b_1,b_2,w_1,w_2,b) (w11,w12,w21,w22,b1,b2,w1,w2,b)
2. 对所有的 w w w: 求 α E α w \frac{\alpha E}{\alpha w} αwαE; 对所有 b b b：求 α E α b \frac{\alpha E}{\alpha b} αbαE
3. w 新 = w 旧 − α α E α w ∣ w 旧 w^新 = w^旧 - \alpha\frac{\alpha E}{\alpha w}|{w^旧} w新=w旧−ααwαE∣w旧
   b 新 = b 旧 − α α E α b ∣ b 旧 b^新 = b^旧 - \alpha\frac{\alpha E}{\alpha b}|{b^旧} b新=b旧−ααbαE∣b旧
4. 当所有 α E α w \frac{\alpha E}{\alpha w} αwαE，以及 α E α b \frac{\alpha E}{\alpha b} αbαE 都为0时，退出。

其中， E E E为期望函数（损失函数）， w , b w,b w,b为参数，其中 b b b为bias，上述3步骤是一个梯度下降的公式，对梯度下降不熟悉的可以看看这篇文章 线性回归 ，有详细讲解。

刚刚讲到的是BP算法的一个整体思路，在神经网络训练过程中，进行梯度计算的时候，使用到的一个核心法则是 链式法则（chain rule），这是微积分中求导数那里的知识点，这里不做赘述，简单讲一下结论：

1. 有 y = g ( x ) , z = h ( y ) y=g(x),z=h(y) y=g(x),z=h(y) 要求 z z z 对 x x x 求导，可以表示为：
   Δ x → Δ y → Δ z \Delta x \rightarrow \Delta y \rightarrow \Delta z Δx→Δy→Δz
   d z d x = d z d y ⋅ d y d x \frac{dz}{dx}=\frac{dz}{dy} · \frac{dy}{dx} dxdz=dydz⋅dxdy

2. 有 x = g ( s ) , y = h ( s ) , z = k ( x , y ) x=g(s), y=h(s), z=k(x,y) x=g(s),y=h(s),z=k(x,y) 要求 z z z 对 s s s 求导，可以表示为：
   

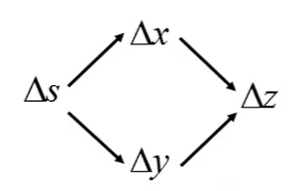
   即： d z d s = ∂ z ∂ x d x d s + ∂ z ∂ y d y d s \frac{dz}{ds}=\frac{\partial z}{\partial x}\frac{dx}{ds}+\frac{\partial z}{\partial y} \frac{dy}{ds} dsdz=∂x∂zdsdx+∂y∂zdsdy

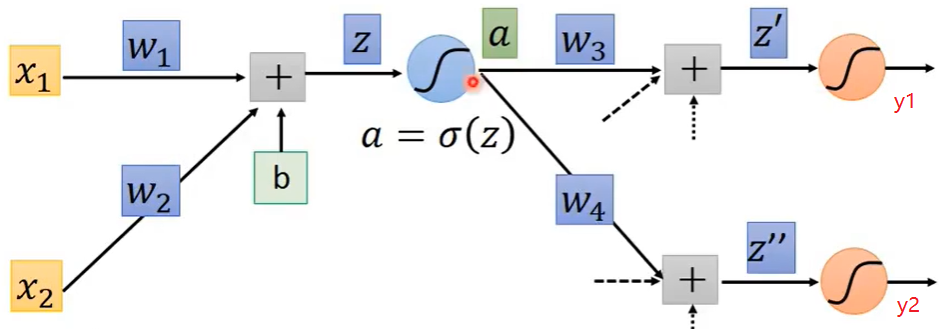
这里为了便于理解，假设不要关注虚线部分的值（其实计算方式是一样）

前向传播：

① z = x 1 w 1 + x 2 w 2 + b 11 z=x_1w_1+x_2w_2+b_{11} z=x1w1+x2w2+b11;

② a = σ ( z ) a=\sigma(z) a=σ(z)

③ z , = a w 3 + b 21 z^,=aw_3+b_{21} z,=aw3+b21

④ z , , = a w 4 + b 22 z^{,,}=aw_4+b_{22} z,,=aw4+b22

⑤ y 1 = σ ( z , ) y_1=\sigma(z^,) y1=σ(z,)

⑥ y 2 = σ ( z , , ) y_2=\sigma(z^{,,}) y2=σ(z,,)

反向传播：这里只讲一个示例，假设我要计算 w 1 w_1 w1的梯度，更新它。假设该神经网络的损失函数记为C。

那么我要计算的是： ∂ C ∂ w 1 \frac{\partial C}{\partial w_1} ∂w1∂C

由链式法则可得： ∂ C ∂ w 1 = ∂ C ∂ z ∂ z ∂ w 1 \frac{\partial C}{\partial w_1}=\frac{\partial C}{\partial z}\frac{\partial z}{\partial w_1} ∂w1∂C=∂z∂C∂w1∂z
∂ C ∂ z = ∂ C ∂ a ∂ a ∂ z \frac{\partial C}{\partial z}=\frac{\partial C}{\partial a}\frac{\partial a}{\partial z} ∂z∂C=∂a∂C∂z∂a； ∂ C ∂ a = ∂ C ∂ z , ∂ z , ∂ a + ∂ C ∂ z , , ∂ z , , ∂ a \frac{\partial C}{\partial a}=\frac{\partial C}{\partial z^,}\frac{\partial z^,}{\partial a}+\frac{\partial C}{\partial z^{,,}}\frac{\partial z^{,,}}{\partial a} ∂a∂C=∂z,∂C∂a∂z,+∂z,,∂C∂a∂z,,； ∂ C ∂ z , = ∂ C ∂ y 1 ∂ y 1 ∂ z , \frac{\partial C}{\partial z^,}=\frac{\partial C}{\partial y_1}\frac{\partial y_1}{\partial z^,} ∂z,∂C=∂y1∂C∂z,∂y1； ∂ C ∂ z , , = ∂ C ∂ y 2 ∂ y 2 ∂ z , , \frac{\partial C}{\partial z^{,,}}=\frac{\partial C}{\partial y_2}\frac{\partial y_2}{\partial z^{,,}} ∂z,,∂C=∂y2∂C∂z,,∂y2；

得到： ∂ C ∂ w 1 = ( ∂ C ∂ y 1 ∂ y 1 ∂ z , ∂ z , ∂ a + ∂ C ∂ y 2 ∂ y 2 ∂ z , , ∂ z , , ∂ a ) ∂ a ∂ z ∂ z ∂ w 1 \frac{\partial C}{\partial w_1}=(\frac{\partial C}{\partial y_1}\frac{\partial y_1}{\partial z^,}\frac{\partial z^,}{\partial a}+\frac{\partial C}{\partial y_2}\frac{\partial y_2}{\partial z^{,,}}\frac{\partial z^{,,}}{\partial a})\frac{\partial a}{\partial z}\frac{\partial z}{\partial w_1} ∂w1∂C=(∂y1∂C∂z,∂y1∂a∂z,+∂y2∂C∂z,,∂y2∂a∂z,,)∂z∂a∂w1∂z

这样就可以求得 w 1 w_1 w1的梯度了，假设C的函数表达式为： C = 1 2 [ ( y 1 − t 1 ) 2 + ( y 2 − t 2 ) 2 ] C=\frac{1}{2}[(y_1-t_1)^2+(y_2-t_2)^2] C=21[(y1−t1)2+(y2−t2)2]，其中 t 1 , t 2 t_1,t_2 t1,t2为目标真实值。激活函数 σ ( x ) \sigma(x) σ(x)为sigmoid函数，其导数为 σ , ( x ) = σ ( x ) ( 1 − σ ( x ) ) \sigma ^,(x)=\sigma(x)(1-\sigma(x)) σ,(x)=σ(x)(1−σ(x))。

基于上述约定，通过反向传播链式法则推导出的 ∂ C ∂ w 1 \frac{\partial C}{\partial w_1} ∂w1∂C完整公式为： ∂ C ∂ w 1 = [ ( ( y 1 − t 1 ) ⋅ y 1 ( 1 − y 1 ) ) ⋅ w 3 + ( ( y 2 − t 2 ) ⋅ y 2 ( 1 − y 2 ) ) ⋅ w 4 ] ⋅ a ( 1 − a ) ⋅ x 1 \frac{\partial C}{\partial w_1} = \left[ \Big( (y_1 - t_1) \cdot y_1(1 - y_1) \Big) \cdot w_3 + \Big( (y_2 - t_2) \cdot y_2(1 - y_2) \Big) \cdot w_4 \right] \cdot a(1 - a) \cdot x_1 ∂w1∂C=[((y1−t1)⋅y1(1−y1))⋅w3+((y2−t2)⋅y2(1−y2))⋅w4]⋅a(1−a)⋅x1

由这个算出来的值，使用上述梯度更新公式： w 新 = w 旧 − α α E α w ∣ w 旧 w^新 = w^旧 - \alpha\frac{\alpha E}{\alpha w}|_{w^旧} w新=w旧−ααwαE∣w旧 就可以得到更新后的参数 w 1 w_1 w1，同样的计算神经网络每一个参数，最终更新整个网络的参数集，就这样一步一步找到最优解。

这就是神经网络反向传播算法，更新参数的全部过程。

2、激活函数选择

激活函数是神经网络能拟合各种决策面的关键，它为神经网络带来了非线性，激活函数几乎每一层都会使用到它，在神经网络的搭建中，激活函数的选择非常重要，通常需要考虑到任务、网络架构等各个方面。

1. sigmoid 一般用于二分类问题的输出层，sigmoid函数的值域是在 ( 0 , 1 ) (0,1) (0,1)具有天然的二分类优势，可以通过sigmoid输出的一个概率值来记为正类概率，1-(该概率值)记为负概率，这样就能区分开两种类别。sigmoid有一个缺陷就是它用在隐藏层容易造成梯度消失 ，它在取值范围>6或者<-6的时候导数就趋近于零，无法反向传播计算梯度，或者说梯度太小导致参数跟新极其缓慢，它的导函数的取值范围为 ( 0 , 0.25 ) (0, 0.25) (0,0.25)，随着层数的增加，非常容易导致梯度消失问题。一般来说使用sigmoid的隐藏层在5层之内就会发生梯度消失问题。
2. tanh 是类似于sigmoid的激活函数，一般在RNN及其变体中使用的较多 ，使用它作为一个门单元的激活处理，它也有一个类似于sigmoid的缺陷，它也容易发生梯度消失 ，因为它在定义域 ( − 3 , 3 ) (-3,3) (−3,3)的时候梯度比较大，当超出这个范围时，梯度会接近于0。它的导数值域范围为 ( 0 , 1 ) (0,1) (0,1)。
3. relu 的函数形式非常简单，在大于0的位置 y = x y=x y=x，在小于0的位置，恒为0。这让它有一个非常优异的特点：计算神经科学提出"稀疏激活"对信息处理更高效，而ReLU能天然产生稀疏激活（一半的神经元输出为0），缓解了过拟合问题 。ReLU提出时间很早，但是沉寂了许久，AlexNet 这篇论文对它的推动起到了至关重要的作用。ReLU相比sigmoid还有一个重要的优势是其计算复杂度小 ，sigmoid函数涉及指数计算，而ReLU仅为max(0, x)。ReLU最重要的一个特征是它可以有效的缓解梯度消失问题 ，在<0的位置神经元是饱和的，在>0的位置神经元恒定为非饱和，这就导致梯度在大于零的位置不衰减，从而缓解梯度消失问题。随着训练的推进部分值会落入负区间，导致神经元死亡。
4. Leaky ReLU 是针对relu的神经元死亡问题提出的改进版，他的函数表达式略有改动，在负区间不再是0，而是一个线性的小梯度值。但是实际使用还是relu比较多。
5. softmax 常用来与多分类交叉熵配合使用 ，见名知意，它主要是用来做多分类任务。它可以把输出层输出的分数值转换为概率值，且总和为一。
6. GELU 广泛用于Transformer架构的模型中，GELU 在输入为负时，并不会像 ReLU 那样将输出压制为 0，而是通过引入一个概率值，允许小的负输出。

这里只是对激活函数做了一个简单的介绍，这篇博客 《激活函数》 对常用的激活函数做了更加细致的讲解，包括函数表达式、函数图像等。

激活函数选择策略：

1. 一般在隐藏层中，选择的优先级一般为： R e L U > L e a k y R e L U > P R e L U > T a n h > S i g m o i d ReLU > Leaky\space ReLU > PReLU > Tanh > Sigmoid ReLU>Leaky ReLU>PReLU>Tanh>Sigmoid

2. 对于二分类任务的输出层选择：
   S i g m o i d + B C E L o s s 或 S o f t m a x + C r o s s E n t r o p y L o s s Sigmoid + BCELoss \space\space或\space\space Softmax+CrossEntropyLoss Sigmoid+BCELoss 或 Softmax+CrossEntropyLoss

3. 对于多分类任务输出层选择：
   S o f t m a x + C r o s s E n t r o p y L o s s Softmax+CrossEntropyLoss Softmax+CrossEntropyLoss

4. 回归任务输出层：

   默认不激活

5. 回归值必须 ≥ 0 \geq 0 ≥0:

   选择ReLU

6. 回归值在 ( 0 , 1 ) (0, 1) (0,1) 之间：

   选择Sigmiod（需对标签归一化）

7. 回归值在 ( − 1 , 1 ) (-1, 1) (−1,1):

   选择Tanh（需对标签归一化）

3、训练数据初始化

可以考虑在数据输入时使用归一化操作，它可以让决策面更加的均匀。

将特征值归一化为均值为0 ，方差为1 ，的标准正态分布。
X = x − E [ x ] V a r [ x ] + ϵ X = \frac{x-E[x]}{\sqrt{Var[x]+\epsilon}} X=Var[x]+ϵ x−E[x]

其中， E [ x ] E[x] E[x] 代表期望， V a r [ x ] Var[x] Var[x] 代表方差， ϵ \epsilon ϵ 为了防止除零。

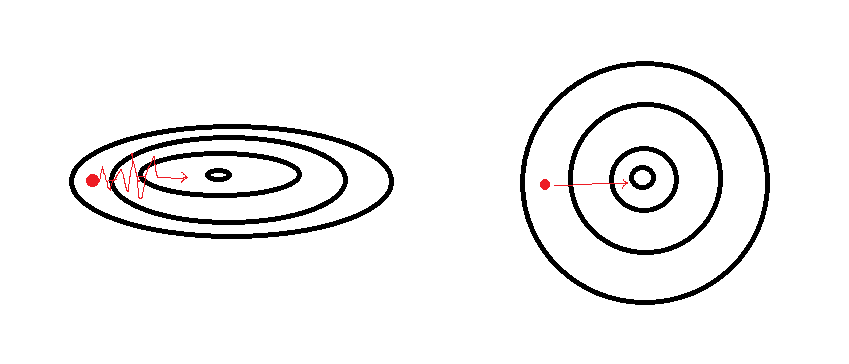
如图所示，假设其为代价函数的等高线图，在未作归一化操作时，代价函数更为狭长，在这样的函数上寻找最优解往往更加困难，会需要很小的学习率，因为搜索路径会来回震荡。而像图右边的更圆的等高线，初始值无论从哪里开始都能够直达最小值，不会产生震荡，这时可以采用较大的学习率加速收敛。总的来说，对输入特征做归一化是可以加速模型收敛的。
一般来说，这种做法尤其是适用于不同特征之间的量纲不一致的情况，这样可以极大的减小模型受量纲影响程度。但是一般情况下都做一下也是不错的，因为它并没有什么坏处，同时也可以消除极端值的影响。

4、参数的初始化

参数的选择直接影响到解的搜索。如果 w T x + b w^Tx+b wTx+b一开始很大或很小，那么梯度将趋近于0，反向传播后与之相关的梯度也趋近于0，导致训练缓慢。参数随机到0附近是一个很好的选择。

参数初始化的作用：

1. 防止梯度消失或爆炸
2. 提高收敛速度
3. 打破对称性（对称性指的是：神经元、权重、输入完全相同）

常用的方法：

1. 均匀分布初始化
   W ∼ U ( − 1 d , 1 d ) W\sim U(\frac{-1}{\sqrt d},\frac{1}{\sqrt d}) W∼U(d −1,d 1)
2. 正态分布初始化
   W ∼ N ( 0 , σ 2 ) W ∼ N(0, σ²) W∼N(0,σ2)
3. 全0、全1初始化
4. 固定值初始化
5. KaiMing初始化（也叫He初始化）
   ① 凯明正态分布初始化： W ∼ N ( 0 , 2 d i n ) W\sim N(0, \sqrt{\frac{2}{d_{in}}}) W∼N(0,din2 )
   ② 凯明均匀分布初始化： W ∼ U ( − 6 d i n , 6 d i n ) W\sim U(-\sqrt{\frac{6}{d_{in}}}, \sqrt{\frac{6}{d_{in}}}) W∼U(−din6 ,din6 )
6. Xavier初始化（也叫Glorot初始化）
   ① 泽维尔正态分布初始化： W ∼ N ( 0 , 2 d i n + d o u t ) W\sim N(0, \sqrt{\frac{2}{d_{in}+d_{out}}}) W∼N(0,din+dout2 )
   ② 泽维尔均匀分布初始化： W ∼ U ( − 6 d i n + d o u t , 6 d i n + d o u t ) W\sim U(-\sqrt{\frac{6}{d_{in}+d_{out}}}, \sqrt{\frac{6}{d_{in}+d_{out}}}) W∼U(−din+dout6 ,din+dout6 )

一般隐藏层首选的话就是He初始化和Xavier初始化，当然有一些特殊的也需要其他初始化方式，比如BN层的动态可学习参数 γ \gamma γ， β \beta β，一般分别初始化为1，0。另外，LSTM中有些门需要一开始尽量保持关闭或打开，就需要固定一个值得初始化，比如输入门需要尽量抑制，也就是偏置为负，来防止内部状态漂移；输出门也一样需要抑制，防止memory被乱用；遗忘门需要被激活为正，用于保持梯度流动和长期记忆（这里不懂得可以去先看一下LSTM架构）。

5、目标函数的选择

1. 为了缓解过拟合，一般考虑在目标函数中添加上正则化项。
2. 如果是分类问题， f ( w ) f(w) f(w)可以采用 s o f t m a x softmax softmax函数和交叉熵的组合。
3. 回归问题损失函数选择为：MAE、MSE、SmoothL1
   MAE ： L = 1 n ∑ i = 1 n ∣ y i − y ^ i ∣ L = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}i| L=n1∑i=1n∣yi−y^i∣
   MSE ： L = 1 n ∑ i = 1 n ( y i − y ^ i ) 2 L = \frac{1}{n} \sum{i=1}^{n} (y_i - \hat{y}i)^2 L=n1∑i=1n(yi−y^i)2
   SmoothL1 ： L SmoothL1 = 1 n ∑ i = 1 n { 0.5 ⋅ ( x i ) 2 if ∣ x i ∣ < 1 ∣ x i ∣ − 0.5 if ∣ x i ∣ ≥ 1 L{\text{SmoothL1}} = \frac{1}{n} \sum_{i=1}^n \begin{cases} 0.5 \cdot (x_i)^2 & \text{if } |x_i| < 1 \\ |x_i| - 0.5 & \text{if } |x_i| \geq 1 \end{cases} LSmoothL1=n1i=1∑n{0.5⋅(xi)2∣xi∣−0.5if ∣xi∣<1if ∣xi∣≥1
   交叉熵： 定义目标函数为 E = − ∑ i = 1 N p i ∗ l o g ( q i ) E=-\sum\limits_{i=1}^N p_i * log(q_i) E=−i=1∑Npi∗log(qi)
   如果 F ( w ) F(w) F(w)是 s o f t m a x softmax softmax函数和交叉熵的组合，那么求导将会有非常简单的形式：
   ∂ E ∂ z i = q i − p i \frac{\partial E}{\partial z_i}=q_i - p_i ∂zi∂E=qi−pi

6、参数更新策略

深度神经网络会有梯度累积效应。

（1）SGD的问题：优化路径被迫Z形。

（2）SGD梯度过于随机，优化方向也变得随机。

6.1 优化策略：

1. momentum（动量法）

   在梯度下降过程中，解有可能会落入critical point ，比如鞍点 （saddle point）或者局部最小值 （local minima）。因为这些点的梯度值为0了，要解决这样的问题就需要在突然落入critical point的时候还能够进行梯度更新。动量法可以做到这一点，动量法的思想是以累计梯度来代替反向传播公式中的梯度，让当前时刻更新参考了之前的步骤，方法是使用指数加权平均法。动量法可以使得每一次的梯度更新会包含了之前步骤的一个梯度信息 ，这样的话在落入critical point的时候还能够进行梯度更新。

   公式： g t = ∇ L ( w t − 1 ) g_t=\nabla L(w_{t-1}) gt=∇L(wt−1) m t = β m t − 1 + ( 1 − β ) g t m_t=\beta m_{t-1}+(1-\beta)g_t mt=βmt−1+(1−β)gt
   

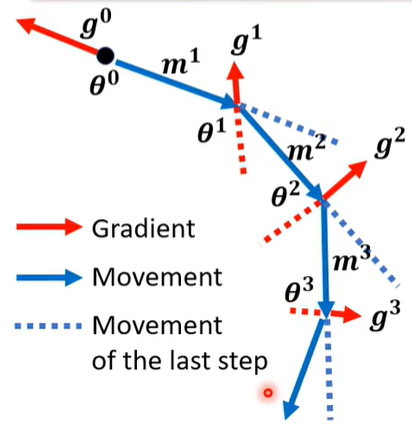
   可以看到图中每一次的参数更新方向都会受到之前梯度的影响。

   形象的来讲类似于一个小球，在从坡顶滚入低谷的时候虽然中间会存在小坑，但小球还是会借助动量冲出小坑，继续向着最低点前进，动量法的名称也是源自于此。
   

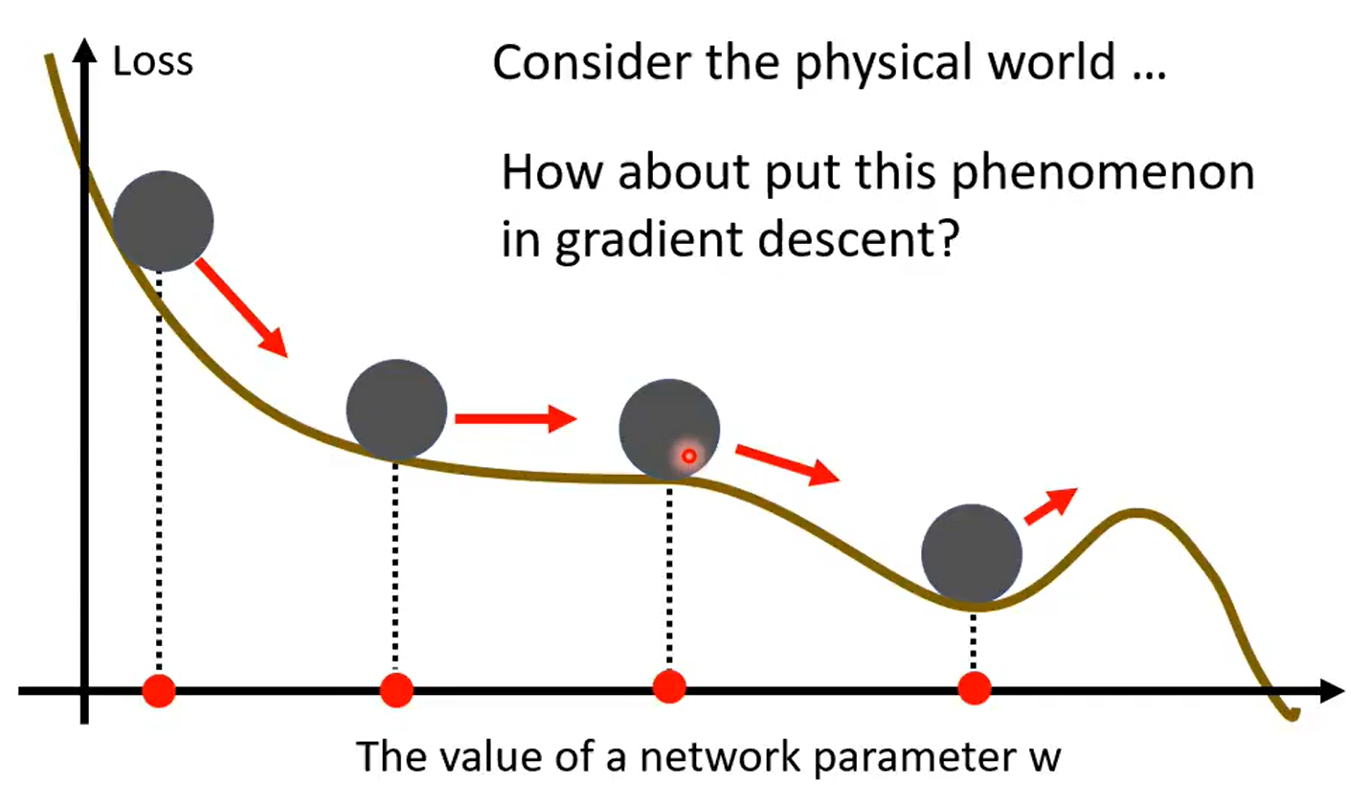
2. AdaGrad

   另外一个方法是Adagrad方法，它的公式为
   g t = ∇ L ( w t − 1 ) g_t=\nabla L(w_{t-1}) gt=∇L(wt−1) s t = 1 t + 1 ∑ i = 0 t ( g i t ) 2 s_t=\sqrt{\frac{1}{t+1}\sum\limits_{i=0}^t(g_i^t)^2} st=t+11i=0∑t(git)2

   参数更新公式为： w t = w t − 1 − η s t + ϵ g t w_t=w_{t-1}-\frac{\eta}{s_t+\epsilon}g_t wt=wt−1−st+ϵηgt

   当 s t s_t st变小了， η s t \frac{\eta}{s_t} stη就变大了，步长也就变大了。

3. RMSProp

   它的公式为
   g t = ∇ L ( w t − 1 ) g_t=\nabla L(w_{t-1}) gt=∇L(wt−1) s t = α ( s t − 1 ) 2 + ( 1 − α ) ( g i t ) 2 s_t=\sqrt{\alpha(s_{t-1})^2+(1-\alpha)(g_i^t)^2} st=α(st−1)2+(1−α)(git)2

   这里使用的是二阶矩增加权重 。

   参数更新公式为： w t = w t − 1 − η s t + ϵ g t w_t=w_{t-1}-\frac{\eta}{s_t+\epsilon}g_t wt=wt−1−st+ϵηgt

4. Adam
   一阶矩+二阶矩的自适应优化 。它使用了momentum和RMSProp的思想，同时在梯度中添加了一个权重衰减（L2正则） ，也称为Frobenius范数。
   g t = ∇ L ( w t − 1 ) + λ w t − 1 g_t=\nabla L(w_{t-1})+\lambda w_{t-1} gt=∇L(wt−1)+λwt−1 m t = β m t − 1 + ( 1 − β ) g t m_t=\beta m_{t-1}+(1-\beta)g_t mt=βmt−1+(1−β)gt
   s t = α ( s t − 1 ) 2 + ( 1 − α ) ( g i t ) 2 s_t=\sqrt{\alpha(s_{t-1})^2+(1-\alpha)(g_i^t)^2} st=α(st−1)2+(1−α)(git)2

   这里进行了一个偏差修正：
   m ^ t = m t 1 − β 1 t \hat m_t=\frac{m_t}{1-\beta_1^t} m^t=1−β1tmt s ^ t = s t 1 − β 2 t \hat s_t=\frac{s_t}{1-\beta_2^t} s^t=1−β2tst

   最终的参数更新公式为：
   w t = w t − 1 − η s ^ t + ϵ m ^ t w_t=w_{t-1}-\frac{\eta}{\hat s_t+\epsilon}\hat m_t wt=wt−1−s^t+ϵηm^t

5. AdamW

   Adam中把L2放在 g t g_t gt中会被梯度缩放 β 1 \beta_1 β1影响，正则化强度在不同参数之间被不均匀的缩放了，易过拟合。AdamW优化了这一点，将权重衰减解耦合 了，把它拿到外面直接衰减参数，与梯度无关！公式为：
   w t = w t − 1 η s ^ t + ϵ m ^ t − η λ w t − 1 w_t=w_{t-1}\frac{\eta}{\hat s_t+\epsilon}\hat m_t - \eta \lambda w_{t-1} wt=wt−1s^t+ϵηm^t−ηλwt−1

6.2 学习率的调度：

为什么要用学习率的调度：

早期阶段：希望快速下降到较优区域->学习率大

中后期：希望稳定收敛，细化局部最优->学习率小

这里列举一些常用的方法：

1. step decay（阶梯下降）
2. Exponential Decay（指数衰减）
3. polynomial Decay（多项式衰减）
4. Cosine Annealing（余弦退火策略）
5. Cyclical Learning Rate
6. Warm up

warm up为什么先增后减：一个可能的解释是在使用adam时不需要一开始就过分关注s的大小，因为一开始的s并没有统计太多的梯度信息，我们需要在一段时间之后再给一个初始大的 η \eta η比较能代表梯度信息。