一、随机事件
1、随机试验
(1)随机试验具有三个特点:
①可重复性:可以在相同的条件下重复地进行。
②可预知性:每次试验的结果可能不止一个,且事先知道试验的所有可能结果。
③不确定性:每次试验之前不能确定哪个结果会发生。
(2)随机试验通常记为E,如射击实验、抛硬币实验。
2、样本空间与样本点
(1)样本空间:

(2)样本点:

3、随机事件

4、例题
写出下列试验的样本空间

二、事件间的关系与运算
1、事件间的关系
(1)事件的包含:
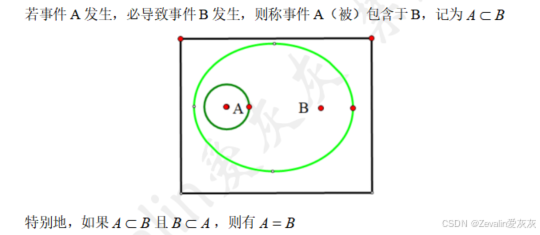
(2)互不相容事件(互斥事件):
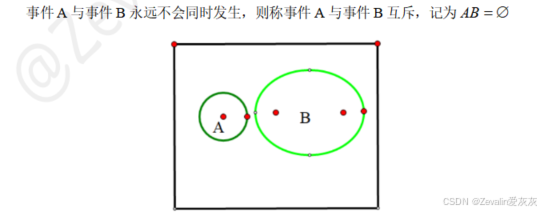
(3)对立事件(互逆事件):
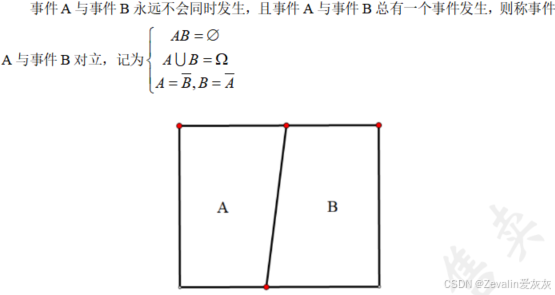
2、事件间的运算
(1)事件的和:
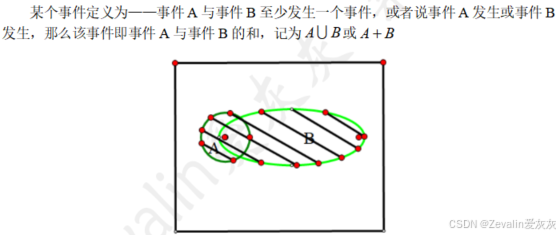
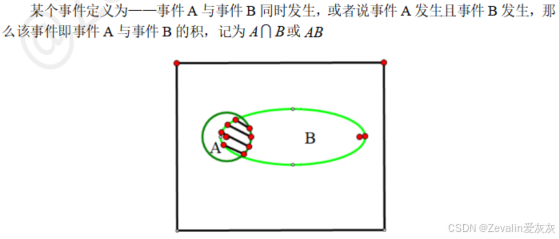
(2)事件的积:
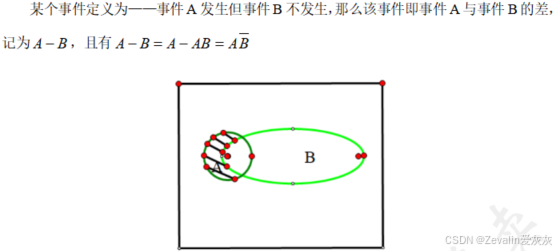
(3)事件的差:
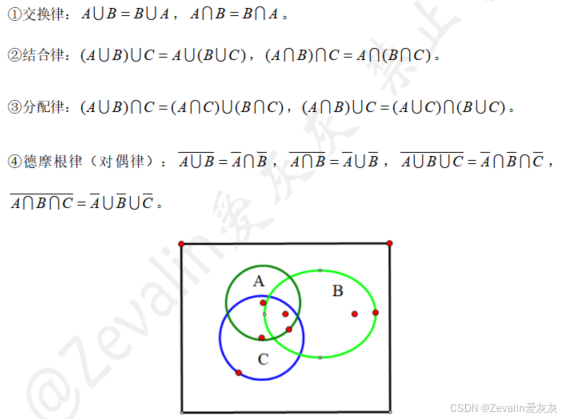
(4)事件运算满足的定律:
3、例题


三、概率的定义与性质
1、概率的统计性定义
(1)频率:

(2)概率:

2、概率的性质

3、重要公式
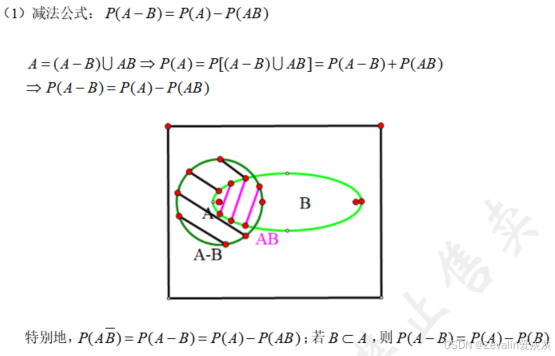
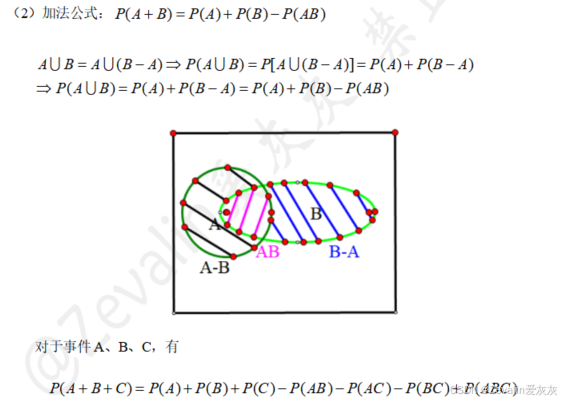
将该公式推广至n个事件相加,则最终事件发生的概率计算如下,n个事件中分别选取1~n个事件进行组合,所有能组成的组合各自构成新事件,最终事件发生的概率为------选取奇数个事件组合构成的新事件的发生概率相加,减去选取偶数个事件组合构成的新事件的发生概率(简记为"加奇减偶")
4、例题

四、古典概型
1、古典概型的特点与计算公式
(1)古典概型的特点:
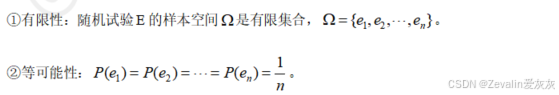
(2)计算公式:

2、例题
(1)例1:一袋中有5个白球、6个黑球,从中任意取出2球,做不放回抽样。
①求取出的2球为"1白1黑"的概率。
排列思想:设事件A为"1白1黑",它可分解为先抽出1个黑球再抽出1个白球以及先抽出1个白球再抽出1个黑球两个事件,而样本空间为依次从袋中的11个球中抽取2球,于是有
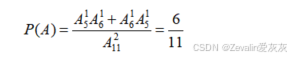
组合思想:设事件A为"1白1黑",即从袋中的任意5个白球中抓取1个白球,并从袋中的任意6个白球中抓取1个白球,而样本空间为从袋中的11个球中任意抽取2球,于是有
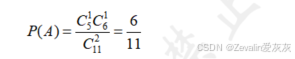
②求取出的2球为"至少1黑"的概率。
设事件B为"至少1黑",那么事件B的互斥事件为"2白0黑",即从袋中的任意5个白球中抓取2个白球,并从袋中的任意6个白球中抓取0个白球,而样本空间为从袋中的11个球中任意抽取2球,于是有
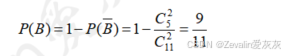
(3)例3:一袋中装有1~5号5个球,从袋中有放回地取3次球,每次取1个球,求3个球的号码组成的3位数为奇数的概率。
设事件A为"3个号码组成的数是奇数",即从1~5号5个球中任抽1球作为百位数,从1~5号5个球中任抽1球作为十位数,再从1、3、5号3个球中任抽1球作为个位数,而样本空间为从1~5号5个球中有放回地任抽3球,于是有
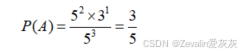
五、几何概型
1、几何概型的特点与计算公式
(1)几何概型的特点:

(2)计算公式:

2、例题


六、条件概率与乘积公式
1、条件概率
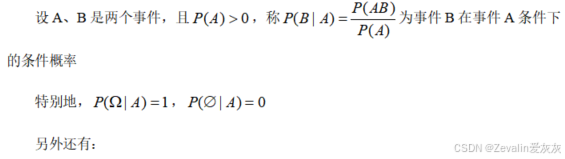
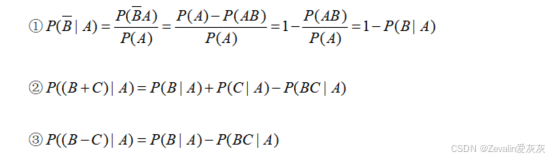
2、乘积公式

3、例题

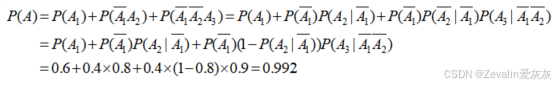
七、全概率公式与贝叶斯公式
1、完备事件组

2、全概率公式

3、贝叶斯公式

4、样本空间的划分方法

5、例题
(1)例1:设甲袋中装有n个白球和m个红球,乙袋中装有N个白球和M个红球,现从甲袋中任意取一个球放入乙袋中,再从乙袋中任意取一个球,试求取到白球的概率是多少。

(2)例2:发报台分别以概率0.6和0.4发出信号A和B,由于系统受到干扰,当发出信号A时,收报台分别以概率0.8和0.2收到信号A和B,当发出信号B时,收报台分别以概率0.9和0.1收到信号B和A,如果收报台收到信号A,试求发报台发出信号A的概率是多少。


八、事件的独立性
1、事件的独立

2、独立的性质


3、多个事件的独立性

4、例题

九、伯努利概型
1、伯努利试验

2、二项概率公式

3、例题
