leetcode算法（112.路径总和）

cpp 复制代码

class Solution {
private:
    // 递归遍历函数，cur表示当前节点，count表示当前还需要凑足的和
    bool traversal(TreeNode* cur, int count) {
        // 如果当前节点是叶子节点，并且count已经减到0，说明找到了一条路径
        if (cur->left==NULL && cur->right==NULL && count == 0) return true; 
        // 如果当前节点是叶子节点但count不为0，说明这条路径和不符合要求
        if (cur->left==NULL && cur->right==NULL && count!=0) return false; 

        // 如果存在左子节点
        if (cur->left) { // 左
            count -= cur->left->val; // 递归前：将左子节点的值从count中减去（进入路径）
            if (traversal(cur->left, count)) return true; // 递归进入左子树
            count += cur->left->val; // 回溯：恢复count的值（撤销选择）
        }
        
        // 如果存在右子节点
        if (cur->right) { // 右
            count -= cur->right->val; // 递归前：将右子节点的值从count中减去（进入路径）
            if (traversal(cur->right, count)) return true; // 递归进入右子树
            count += cur->right->val; // 回溯：恢复count的值（撤销选择）
        }
        
        // 左右子树都没有找到符合条件的路径
        return false;
    }

public:
    // 判断是否存在从根节点到叶子节点的路径，其节点值之和等于sum
    bool hasPathSum(TreeNode* root, int sum) {
        // 处理空树的情况
        if (root == NULL) return false;
        // 调用递归函数，初始时已经包含了根节点的值（sum - root->val）
        return traversal(root, sum - root->val);
    }
};

复制代码

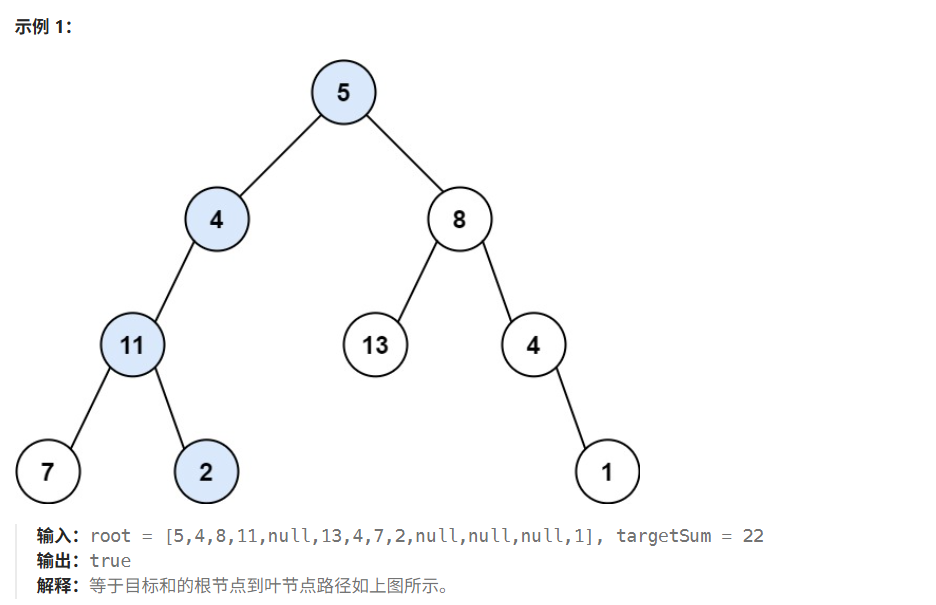
 举例： 
        5
       / \
      4   8
     /   / \
    11  13  4
   /  \      \
  7    2      1

步骤1：主函数调用

cpp 复制代码

hasPathSum(root, 22)

root != NULL，所以继续
调用 traversal(root, 22 - 5)，即 traversal(root, 17)
- 初始 cur = 节点5 ，count = 17

步骤2：进入 traversal(节点5, 17)

节点5不是叶子节点（有左右子节点）
先处理左子树：

cpp 复制代码

if (cur->left) { // 节点5有左子节点4
    count -= cur->left->val;  // count = 17 - 4 = 13
    if (traversal(cur->left, 13)) return true; 
    // 递归进入节点4

}

步骤3：进入 traversal(节点4, 13)

节点4不是叶子节点（有左子节点11）
处理左子树：

cpp 复制代码

if (cur->left) { // 节点4有左子节点11
    count -= cur->left->val;  // count = 13 - 11 = 2
    if (traversal(cur->left, 2)) return true;  // 递归进入节点11
    // 注意：这里进入递归，后面可能找到路径直接返回true
}

步骤4：进入 traversal(节点11, 2)

cpp 复制代码

if (cur->left) { // 节点11有左子节点7
    count -= cur->left->val;  // count = 2 - 7 = -5
    if (traversal(cur->left, -5)) return true;  // 递归进入节点7
}

步骤5：进入 traversal(节点7, -5)

节点7是叶子节点（左右子节点都为空）
检查条件：

cpp 复制代码

if (cur->left==NULL && cur->right==NULL && count == 0)  // false，因为count = -5 ≠ 0
if (cur->left==NULL && cur->right==NULL && count != 0) return false;  
// 满足条件，返回false

返回 false 到步骤4

步骤6：回到 traversal(节点11, 2)

cpp 复制代码

// 左子树递归结束，返回false
// 所以继续将 7 加上
count += cur->left->val;  // count = -5 + 7 = 2（回溯）

// 现在处理右子树
if (cur->right) { // 节点11有右子节点2
    count -= cur->right->val;  // count = 2 - 2 = 0
    if (traversal(cur->right, 0)) return true;  // 递归进入节点2
}

步骤7：进入 traversal(节点2, 0)

节点2是叶子节点
检查条件：

cpp 复制代码

if (cur->left==NULL && cur->right==NULL && count == 0)  
// 完全满足！返回true

返回 true 到步骤6

步骤8：回到 traversal(节点11, 2)

cpp 复制代码

if (traversal(cur->right, 0)) return true;  // 这个调用返回了true
// 所以直接返回true，不再执行后面的回溯

返回 true 到步骤3

步骤9：回到 traversal(节点4, 13)

cpp 复制代码

if (traversal(cur->left, 2)) return true;  // 这个调用返回了true
// 直接返回true

返回 true 到步骤2

步骤10：回到 traversal(节点5, 17)

cpp 复制代码

if (traversal(cur->left, 13)) return true;  // 这个调用返回了true
// 直接返回true，不再处理右子树

返回 true 到步骤1

步骤11：主函数

cpp 复制代码

return traversal(root, sum - root->val);  // 返回true

最终结果为 true

复制代码

开始: 节点5, count=17
├─ 进入左子节点4: count=13
│   ├─ 进入左子节点11: count=2
│   │   ├─ 进入左子节点7: count=-5 → 不是叶子节点or count≠0 → false ⇠
│   │   └─ 进入右子节点2: count=0 → 叶子节点且count=0 → true ✓
│   │       找到路径: 5→4→11→2
│   └─ 返回true ⇠
└─ 返回true ⇠

为什么需要最后(return false)返回false？

复制代码

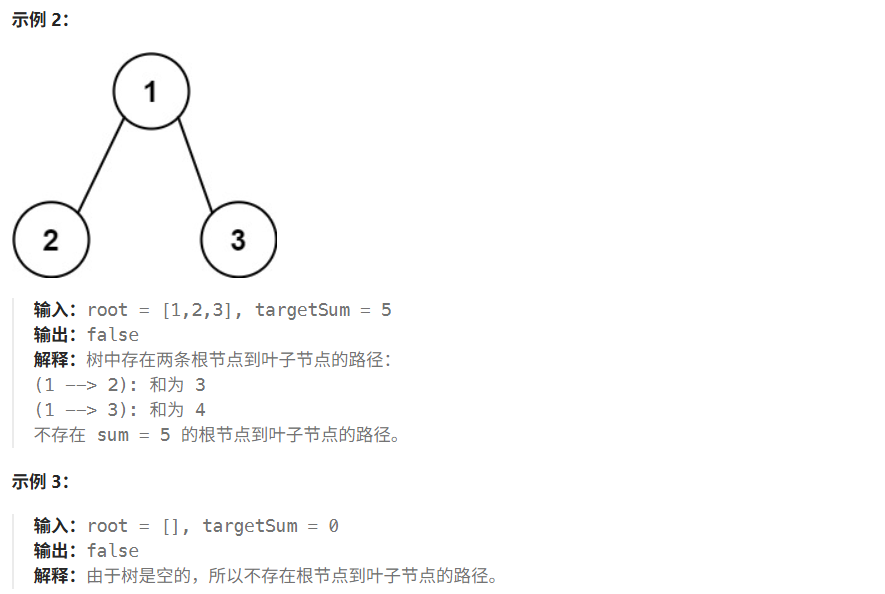
    1
   / \
  2   3          targetSum = 5

步骤1：主函数调用

复制代码

hasPathSum(root, 5)

root != NULL，继续
调用 traversal(root, 5 - 1)，即 traversal(节点1, 4)
- cur = 节点1，count = 4

步骤2：进入 traversal(节点1, 4)

节点1不是叶子节点（有左右子节点2和3）
先处理左子树：

cpp 复制代码

if(cur->left) {  // 节点1有左子节点2，true
    count -= cur->left->val;  // count = 4 - 2 = 2
    if(traversal(cur->left, 2)) return true;  // 递归进入节点2
    // 等待递归结果...
}

步骤3：进入 traversal(节点2, 2)

节点2是叶子节点（左右子节点都为空）
检查条件：

cpp 复制代码

if(cur->left==NULL && cur->right==NULL && count!=0)  // count=2≠0
    return false;  
    // 返回false

返回 false 到步骤2

步骤4：回到 traversal(节点1, 4)

cpp 复制代码

// 左子树递归返回false
count += cur->left->val;  // count = 2 + 2 = 4（回溯）

// 继续处理右子树
if(cur->right) {  // 节点1有右子节点3，true
    count -= cur->right->val;  // count = 4 - 3 = 1
    if(traversal(cur->right, 1)) return true;  // 递归进入节点3
    // 等待递归结果...
}

步骤5：进入 traversal(节点3, 1)

节点3是叶子节点
检查条件：

cpp 复制代码

if(cur->left==NULL && cur->right==NULL && count!=0)  // count=1≠0
    return false;  
    // 返回false

返回 false 到步骤4

步骤6：回到 traversal(节点1, 4)

cpp 复制代码

// 右子树递归返回false
count += cur->right->val;  // count = 1 + 3 = 4（回溯）

// 现在函数执行到这里，需要返回值...
// 问题所在：你的代码缺少 return false; 语句！

这就是问题！

函数执行到这里应该返回 false，因为左右子树都没有找到路径，但代码要有返回语句return false。

cpp 复制代码

return false;  // 左右子树都没有找到路径