1 基础知识
单目深度估计方法分类
- 多目深度估计:该类方法大多需要成对图像或图像序列作为输入、要求相机信息已知,对输入有较强的限制且预测结果首特征选择和匹配的影响较大。
- 双目视觉法:模拟人类利用双眼感知对图像视差而获取深度信息,依赖于图片像素匹配,可以使用模板比对或者对极几何法等匹配方法。
- 立体视觉法:由双目视觉法发展而来,将多个相机设置于视点,或用单目相机在多个不同的视点拍摄图像,增加了算法的稳健性。
- 从运行中恢复形状:利用二维图像序列间的特征点匹配关系,估计相机的运动参数与场景点云信息。
- 三角测量法:借由测量目标点与固定基准线的 已知端点的角度,测量目标距离。
- 单目深度估计:该方法灵活,但由于缺乏深度线索,它是一个不适定性问题(即会出现多个可行解),早期的方法从不同角度提取深度线索进行深度估计。
- 从阴影中恢复形状法:利用图像中物体表面的明暗变化来恢复表面形状。
- 纹理恢复形状法 :通过纹理在经过头是等变形后在图像上的变化来逆向计算深度数据
- 从对焦中获取深度:利用图像中像素的聚焦信息结合摄像机的参数计算图像深度
- 从离焦中获取深度:利用图像中像素的离焦信息结合摄像机的参数计算图像深度
相关数据集
| 名称 | 是否带有深度标签 | 图像分辨率 | 可用图片数量 | 适用场景 | 采集工具 |
|---|---|---|---|---|---|
| NYU depth | 是 | 640*480 | 1449 | 室内 | RGB-D相机 |
| Make3D | 是 | 2272*1704 | 534 | 室外 | LASER |
| KITTI | 是 | 375*1242 | 93000+ | 自动驾驶/室外 | LIDAR |
| Cityscapes | 是 | 1024*2048 | 229733 | 城市 | 相机加人工标注 |
| MegaDepth | 是 | 1600*1600 | 130000+ | 地标/建筑 | SFM+MVS |
| Scene Flow | 是 | 960*540 | 39000+ | 综合 | 人工生成 |
| DIODE | 是 | 1024*768 | 27858 | 综合 | faro |
| Holopix | 否 | 720p or 360p | 50000+ | 综合 | RED Hydrogen One等 |
| Mirror3D | 是 | - | 7011 | 室内 | 人工标注 |
各个数据地址:
- NYU depth:https://cs.nyu.edu/\~fergus/datasets/nyu_depth_v2.html
- Make3D:http://make3d.cs.cornell.edu/data.html
- KITTI:https://docs.ultralytics.com/datasets/detect/kitti/
- Cityscapes:https://www.cityscapes-dataset.com/
- MegaDepth:https://www.cs.cornell.edu/projects/megadepth/
- Scene Flow:https://lmb.informatik.uni-freiburg.de/resources/datasets/SceneFlowDatasets.en.html
- DIODE:https://diode-dataset.org/
- Holopix:https://github.com/leiainc/holopix50k
- Mirror3D:https://3dlg-hcvc.github.io/mirror3d/#/
相关评价指标:
均方根误差(RMSE):能够反映预测结果与真实值之间的绝对误差,受异常值影响较大,无法衡量相对误差。
RMSE=1∣N∣∑∣∣di−di∗∣∣2RMSE=\sqrt{\frac{1}{|N|}\sum{||d_{i}-d_{i}^*||^2}}RMSE=∣N∣1∑∣∣di−di∗∣∣2
对数均方根误差(RMSELog):在RMSE的基础上使用对数运算,减少了异常值的影响,无法衡量相对误差。
RMSELog=1∣N∣∑∣∣logdi−logdi∗∣∣2RMSELog=\sqrt{\frac{1}{|N|}\sum||logd_i-logd_i^*||^2}RMSELog=∣N∣1∑∣∣logdi−logdi∗∣∣2
相对误差(AbsRel):能够反映预测结果与真实值之间的相对误差,差异体现不明显,无法衡量绝对误差。
AbsRel=∑∣di−di∗∣di∗AbsRel=\sum\frac{|d_i-d_i^*|}{d_i^*}AbsRel=∑di∗∣di−di∗∣
平方相对误差(SqRel):在AbsRel的基础上使用平方运算,差异更显著,无法衡量绝对误差。
SqRel=∑∣∣di−di∗∣∣2di∗SqRel=\sum\frac{||d_i-d_i^*||^2}{d_i^*}SqRel=∑di∗∣∣di−di∗∣∣2
准确率(Accuracy):直观地反映出预测结果的准确性,无法衡量预测结果偏离真实值的大小。
Acc:%ofdis.t.max(didi∗,di∗di)=δ<thrAcc: \%\quad of\quad d_i\quad s.t.max(\frac{d_i}{d_i^*},\frac{d_i^*}{d_i})=\delta<thrAcc:%ofdis.t.max(di∗di,didi∗)=δ<thr
2 有监督学习方法
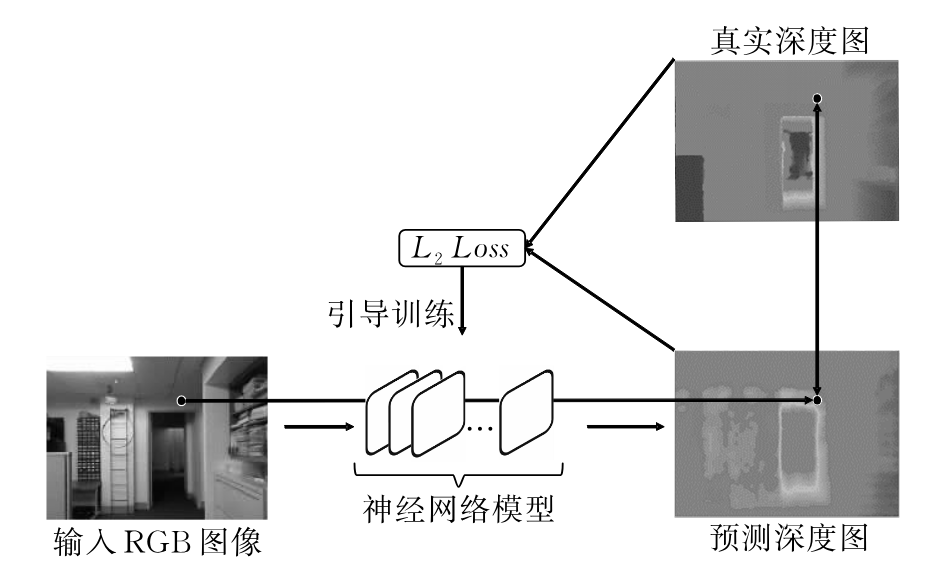
上面这张图清晰的给出了有监督方法的训练流程,神经网络根据输入的RGB图像预测每个像素点的深度值,再通过该预测深度和原始真实深度之间的差异来训练模型。
loss可以使用真实深度图和预测深度图之间的均方损失即,
L2=1∣N∣∑iN∣∣di−di∗∣∣2L_2=\frac{1}{|N|}\sum^{N}_{i}||d_i-d_i^*||^2L2=∣N∣1∑iN∣∣di−di∗∣∣2
虽然有监督训练模型是有真实深度图的,但依然存在全局尺度问题导致估计结果不稳定,譬如,对于一个使用普通房间图片训练得到的深度估计模型,当利用它来估计一个房屋玩具模型图片的深度时,往往会得到比真实值更大的深度估计结果,这是由于图片缺少全局尺度信息,模型并不清除待预测深度的具体范围所导致的,全局尺度模糊将影响模型的泛化能力。
Eigen等最早提出使用卷积神经网络解决深度估计问题,该网络由全局粗略尺度网络和局部精细尺度网络组成。并且Eigen等指出虽然全局尺度发生变化,但场景内的物体之间的深度关系不变(即相对的一个尺度)。在此基础上,他们提出了尺度不变误差:
Lscale=1∣N∣∑iNyi2−λ∣N∣(∑iNyi)2L_{scale}=\frac{1}{|N|}\sum^N_{i}{y_i}^2-\frac{\lambda}{|N|}(\sum^N_iy_i)^2Lscale=∣N∣1∑iNyi2−∣N∣λ(∑iNyi)2
其中yi=log(d)−log(d∗)y_i=log(d)-log(d^*)yi=log(d)−log(d∗),λ\lambdaλ代表权重因子。
将上面的loss拆成两项1∣N∣∑iNyi2\frac{1}{|N|}\sum^N_{i}{y_i}^2∣N∣1∑iNyi2和λ∣N∣(∑iNyi)2\frac{\lambda}{|N|}(\sum^N_iy_i)^2∣N∣λ(∑iNyi)2,我们先分开来看两部分loss,首先是第一部分1∣N∣∑iNyi2\frac{1}{|N|}\sum^N_{i}{y_i}^2∣N∣1∑iNyi2实际上就是每个像素点的均方误差,它的目标是惩罚每个像素预测深度不准,希望 每个点都对,但 单独用它,会强制模型学"绝对尺度"。再来看第二项λ∣N∣(∑iNyi)2\frac{\lambda}{|N|}(\sum^N_iy_i)^2∣N∣λ(∑iNyi)2,整张图的平均 log 偏移,理想情况下如果模型对整张图 统一乘了一个尺度因子,那么所有 yiy_iyi都会整体偏移,∑yi\sum y_i∑yi会变大,loss 反而变小(被减掉)
所以直观来看这个 loss 允许整体尺度变化,但惩罚局部尺度不一致。
Eigen等的实验结果证明了使用神经网络进行深度估计的可行行,那么接下来就是怎么优化:
- 改进网络结构
- 引入与深度相关的辅助信息
- 使用更有效的损失函数监督网络训练