---关注作者,送A/B实验实战工具包
在AB实验的复盘会上,经常出现这样一种诡异的场景:
数据分析师指着大屏幕说:"实验组对比对照组,核心指标提升了 0.05%,P值小于 0.05,结果统计显著 ,建议全量上线。"
产品经理却皱着眉头:"费了半个月开发资源,就涨了 0.05%?这点涨幅连覆盖服务器扩容的成本都不够,这也能叫'显著'?"
这里爆发了一个经典的冲突:统计学的"真" vs 商业上的"值"。
很多刚接触AB实验的团队容易陷入"唯P值论"的误区。今天我们把这两个概念拆开,讲讲为什么显著了不一定能上线,以及如何制定符合商业利益的决策标准。
1. 核心冲突:大样本的"诅咒"
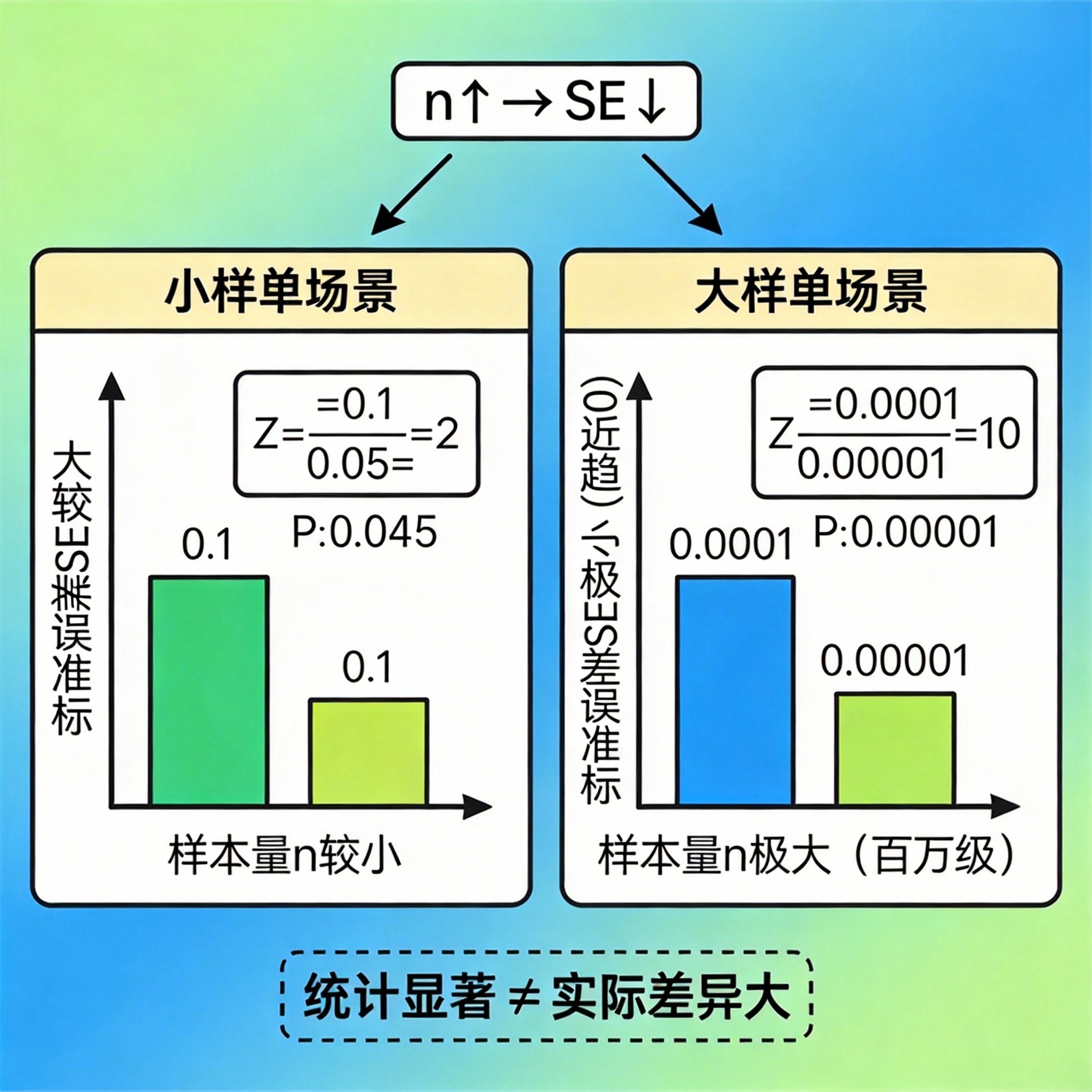
在流量巨大的互联网产品中,我们很容易获得百万级的样本量。根据大数定律和中心极限定理,样本量 (nnn) 越大,标准误差 (SESESE) 就越小。
回顾一下统计检验的核心逻辑(以Z检验为例):
Z=Xˉtreatment−XˉcontrolSE Z = \frac{\bar{X}{treatment} - \bar{X}{control}}{SE} Z=SEXˉtreatment−Xˉcontrol
- Xˉ\bar{X}Xˉ:均值
- SESESE:标准误差,与 1n\frac{1}{\sqrt{n}}n 1 成正比
逻辑推导:
当 nnn 趋向于无穷大时,SESESE 趋向于 0。此时,哪怕分子(两组均值之差)只有微乎其微的 0.0001,算出来的 ZZZ 值也会非常大,从而导致 P 值极小,达成"统计显著"。
结论: 在大数据场景下,统计显著性很容易达成。它只告诉我们"这两个版本有区别",但没告诉我们"这个区别有多大"。
2. 概念辨析:P值 vs 效应量
要解决上述问题,我们需要引入两个维度的评估指标。
2.1 统计显著性 (Statistical Significance)
- 定义:判断实验观察到的差异是否由随机抽样误差引起的概率指标。
- 回答的问题 :Exist?(这种差异是真的存在,还是运气好撞上的?)
- 核心指标 :P值 (P-value)。通常以 α=0.05\alpha = 0.05α=0.05 为界。
2.2 业务显著性 (Practical Significance)
- 定义:实验带来的差异在实际业务场景中是否有价值。
- 回答的问题 :Magnitude?(这种差异有多大?值不值得我折腾?)
- 核心指标 :效应量 (Effect Size)。
在AB实验报告中,我们通常关注以下三种形式的效应量:
A. 相对提升率 (Lift)
最常用的指标,描述涨幅百分比。
Lift=Xˉtreatment−XˉcontrolXˉcontrol×100% Lift = \frac{\bar{X}{treatment} - \bar{X}{control}}{\bar{X}_{control}} \times 100\% Lift=XˉcontrolXˉtreatment−Xˉcontrol×100%
- 痛点解决:直观,老板最爱看。
- 缺陷:当分母(基线)很小时,Lift 会虚高。
B. 绝对增量 (Delta)
描述指标绝对值的变化。
Δ=Xˉtreatment−Xˉcontrol \Delta = \bar{X}{treatment} - \bar{X}{control} Δ=Xˉtreatment−Xˉcontrol
- 痛点解决:对于转化率(Conversion Rate)等本身就是百分比的指标,看绝对增量往往更实在(例如:转化率从 2% 提升到 2.1%,Delta 是 0.1个百分点,Lift 是 5%)。
C. 科恩d值 (Cohen's d)
当我们需要跨实验、跨指标对比"改进程度"时,单纯看 Lift 是不够的,因为不同指标的波动性(方差)不同。Cohen's d 是一个标准化效应量。
d=xˉ1−xˉ2s d = \frac{\bar{x}_1 - \bar{x}_2}{s} d=sxˉ1−xˉ2
- xˉ1,xˉ2\bar{x}_1, \bar{x}_2xˉ1,xˉ2:实验组与对照组的均值。
- sss:综合标准差 (Pooled Standard Deviation),代表数据的波动程度。
- 交互逻辑 :分子代表差异的大小,分母代表数据的噪声。这个公式本质上是在衡量:信号强度是噪声强度的多少倍。
- 判断标准 :通常 d=0.2d=0.2d=0.2 视为小效应,d=0.5d=0.5d=0.5 中等,d=0.8d=0.8d=0.8 大效应。
3. 决策框架:双重门槛 (Dual Thresholds)
成熟的实验决策不应只看 P 值,而应采用"双重门槛"机制。
上线标准 = (P-value < 0.05) AND (Lift > ROI Break-even Point)
3.1 寻找盈亏平衡点 (ROI Break-even Point)
任何改动都有隐性成本:
- 研发成本:开发、测试的人力。
- 维护成本:代码复杂度增加,后续迭代变慢。
- 系统风险:新功能引入潜在 Bug 的概率。
业务显著性阈值 就是那条"生死线"。
例如:某电商公司计算出,如果一个新功能不能带来至少 0.5% 的 GMV 提升,那么它带来的收益甚至无法覆盖服务器扩容和人力维护成本。
那么,0.5% 就是业务显著性的门槛。
3.2 决策四象限
| 统计显著性 (P < 0.05) | 业务显著性 (Lift > 门槛) | 决策建议 |
|---|---|---|
| YES | YES | 全量上线 (双赢) |
| YES | NO | 放弃上线 (鸡肋:虽然是真的提升,但不划算) |
| NO | YES | 继续实验 (潜力股:可能是样本量不足导致 Power 不够,考虑延长实验) |
| NO | NO | 放弃上线 (无效改动) |
4. 进阶技巧:基于置信区间的悲观决策
不要只盯着均值(点估计)看,那是赌徒心态。工程师做决策要看边界。
置信区间 (Confidence Interval, CI) 告诉我们,真实的提升幅度有 95% 的概率落在一个范围内 [Lower,Upper][Lower, Upper][Lower,Upper]。
悲观决策法 (Pessimistic Decision Making):
决策时,看置信区间的下限 (Lower Bound)。
- 场景 :实验显示 Lift 为 +2%,置信区间为 [−0.5%,4.5%][-0.5\%, 4.5\%][−0.5%,4.5%]。
- 虽然均值是正的,但下限是负的。这意味着上线后,最坏情况可能导致指标下跌。决策:不上线或延长观察。
- 场景 :实验显示 Lift 为 +2%,置信区间为 [0.1%,3.9%][0.1\%, 3.9\%][0.1%,3.9%]。业务盈亏平衡点是 0.5%。
- 虽然统计显著(下限 > 0),但下限 0.1% 低于业务成本 0.5%。这意味着虽然大概率是正向收益,但很有可能亏本。决策:谨慎上线。
- 场景 :实验显示 Lift 为 +5%,置信区间为 [1.5%,8.5%][1.5\%, 8.5\%][1.5%,8.5%]。业务盈亏平衡点是 0.5%。
- 下限 1.5% 依然远高于成本线。决策:放心上线。
5. 总结
- 统计显著 ≠\neq= 业务显著:统计显著只代表"差异存在",业务显著代表"差异值钱"。
- 警惕大样本:海量样本下,微小的、无意义的波动也会变得统计显著。
- 双重验证:上线决策必须同时满足统计学门槛(P值)和业务门槛(ROI平衡点)。
- 看下限:用置信区间下限做风控,确保最坏情况下的收益也能覆盖成本。
AB实验的终极目的不是为了得到一个好看的 P 值,而是为了通过科学的手段量化价值,辅助商业决策。
如果这篇文章帮你理清了思路,不妨点个关注,我会持续分享 AB 实验的干货文章。
