拉普拉斯金字塔

简介：个人学习分享，如有错误，欢迎批评指正。

拉普拉斯金字塔 ，把高分辨率图像分解成小分辨率的子图，然后根据之前保留的残差图重构出原始高分辨率图，给定一个输入，然后得到的结果还是原输入。拉普拉斯金字塔可以看作 base + detail 分解，base 就是低分辨率下的低频信号，detail 就是不同尺度下的高频细节。图像的 detail 中只有少部分是高频，大部分细节接近于 0，只要把接近于 0 的那部分数据置为 0，就可以减少数据存储所需空间，同时图像的基本信息不变。实际存储只需要记录每个尺度下的少量高频 + 低分辨率的低频（图面积还小）。除了压缩，拉普拉斯金字塔还有很多应用，如图像拼接（image blending）等。

一、图像金字塔原理

图像金字塔是由一幅图像的多个不同分辨率的子图所构成的图像集合（如下图所示）。该组图像是由单个图像通过不断地降采样所产生的，最小的图像可能仅仅有一个像素点。

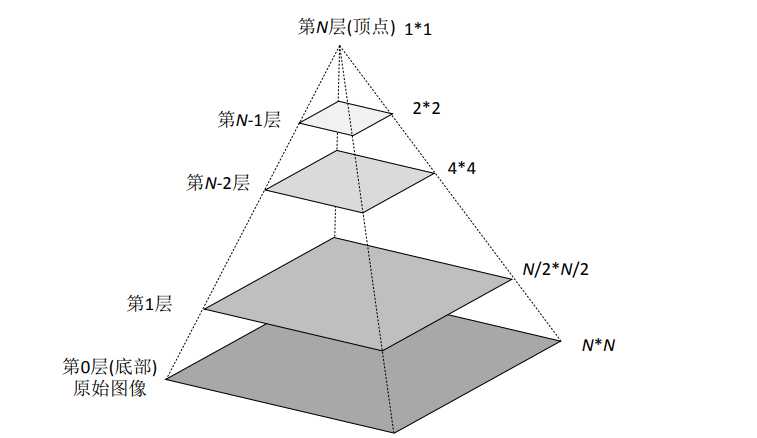
通常情况下，图像金字塔的底部是待处理的高分辨率图像（原始图像），而顶部则为其低分辨率的近似图像。向金字塔的顶部移动时，图像的尺寸和分辨率都不断地降低。通常情况下， 每向上移动一级，图像的宽和高都降低为原来的二分之一。

1.向上采样和向下采样生成金字塔的过程

1.1. 向下采样过程

首先原始图像滤波，得到原始图像的近似图像，然后将近似图像的偶数行和偶数列删除以获取向下采样的结果。有多种滤波器可以选择。例如：

• 邻域滤波器：采用邻域平均技术求原始图像的近似图像。该滤波器能够产生平均金字塔。
• 高斯滤波器：采用高斯滤波器对原始图像进行滤波，得到高斯金字塔。

1.2. 向上采样过程

首先对像素点以补零的方式完成插值。通常是在每列像素点的右侧插入值为零的列，在每行像素点的下方插入值为零的行。如下图所示：左侧是要进行向上采样的 4 个像素点，右侧是向上采样时进行补零后的处理结果。

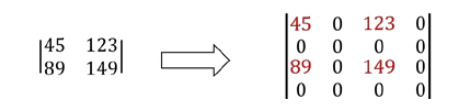
接下来，使用向下采样时所用的高斯滤波器（高斯核）对补零后的图像进行滤波处理 ，以获取向上采样的结果图像。但是需要注意，此时图像中四分之三像素点的值都是零。所以，要将高斯滤波器系数乘以 4，以保证得到的像素值范围在其原有像素值范围内。

二、高斯金字塔

高斯金字塔，概念比较简单，对高分辨率图像先做高斯模糊，再将图像大小缩小到原来的 1/2。多个尺度就构成了高斯金字塔。

缩小这一步实现上比较简单，只要去掉所有奇数行或者偶数行即可。尤其是注意高斯金字塔的第一层和最后一层，第一层就是原始图像，分辨率最高；最后一层是分辨率最小的图像，也是后续拉普拉斯金字塔中的起点。

代码：

cv::Mat pyramid_downsample(const cv::Mat& source) {
    // 收集图像信息
    const int H = source.rows / 2, W = source.cols / 2;
    // 准备一个结果
    cv::Mat downsampled(H, W, source.type());
    const int C = source.channels();
    // 开始每隔一个点采一个样
    for(int i = 0;i < H; ++i) {
        uchar* const res_ptr = downsampled.data + i * W * C;
        for(int j = 0;j < W; ++j)
            std::memcpy(res_ptr + j * C, source.data + 2 * (i * source.cols + j) * C, sizeof(uchar) * C);
    }
    return downsampled;
}

std::vector<cv::Mat> build_gaussi_pyramid(const cv::Mat& source, const int layers_num) {
    // 首先需要把图像规整到 2 ^ layers_num 的整数倍
    const int new_H = (1 << layers_num) * int(source.rows / (1 << layers_num));
    const int new_W = (1 << layers_num) * int(source.cols / (1 << layers_num));
    auto source_croped = source(cv::Rect(0, 0, new_W, new_H)).clone();
    // 准备返回结果
    std::vector<cv::Mat> gaussi_pyramid;
    gaussi_pyramid.reserve(layers_num);
    gaussi_pyramid.emplace_back(source_croped);
    // 开始构造接下来的几层
    for(int i = 1;i < layers_num; ++i) {
        // 先对图像做高斯模糊
        source_croped = fast_gaussi_blur(source_croped, 2, 1.0, 1.0);
        // 做下采样
        source_croped = pyramid_downsample(source_croped);
        // 放到高斯金字塔中
        gaussi_pyramid.emplace_back(source_croped);
    }
    return gaussi_pyramid;
}

如图

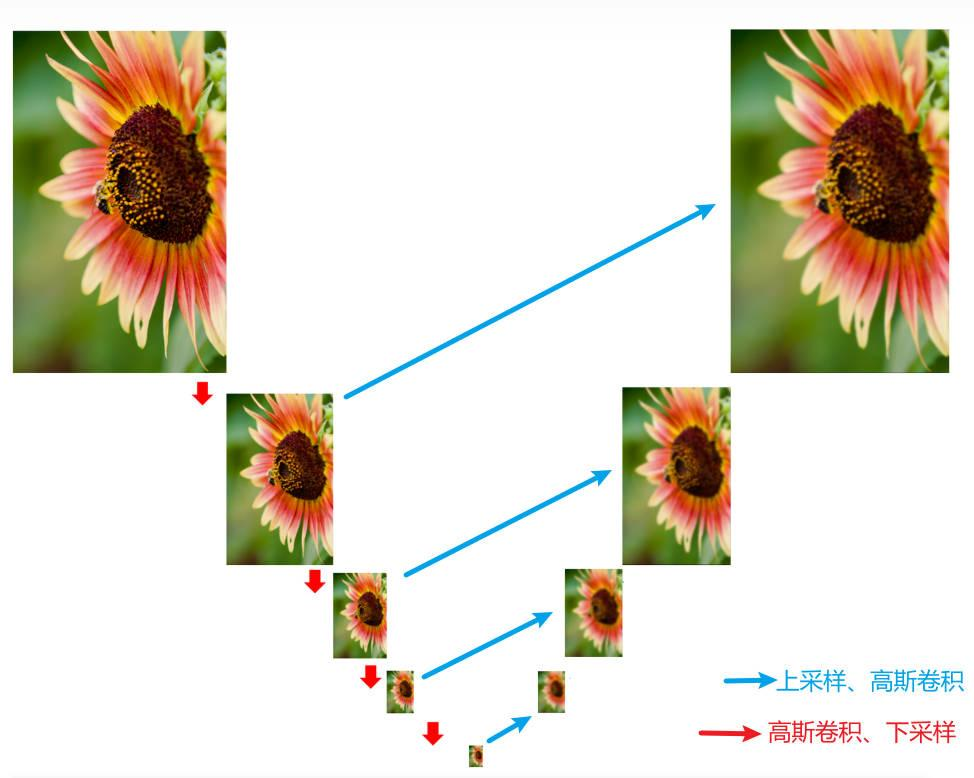
OpenCV 提供了函数 cv2.pyrDown()和函数 cv2.pyrUp()，分别用于实现图像高斯金字塔操作中的向下采样和向上采样，其语法形式为：

dst = cv2.pyrDown( src[, dstsize[, borderType]] )

dst = cv2.pyrUp( src[, dstsize[, borderType]] )

• dstsize 为目标图像的大小。
• borderType 为边界类型， 默认值为 BORDER_DEFAULT ，且仅支持 BORDER_DEFAULT。

注意：如果先对原始图像进行向上采样，再进行向下采样，不会得到原始图像，即不可逆 ！

因为在此操作的过程中，经过删除列和行，会有信息的丢失。

向下采样运行结果图，如下：

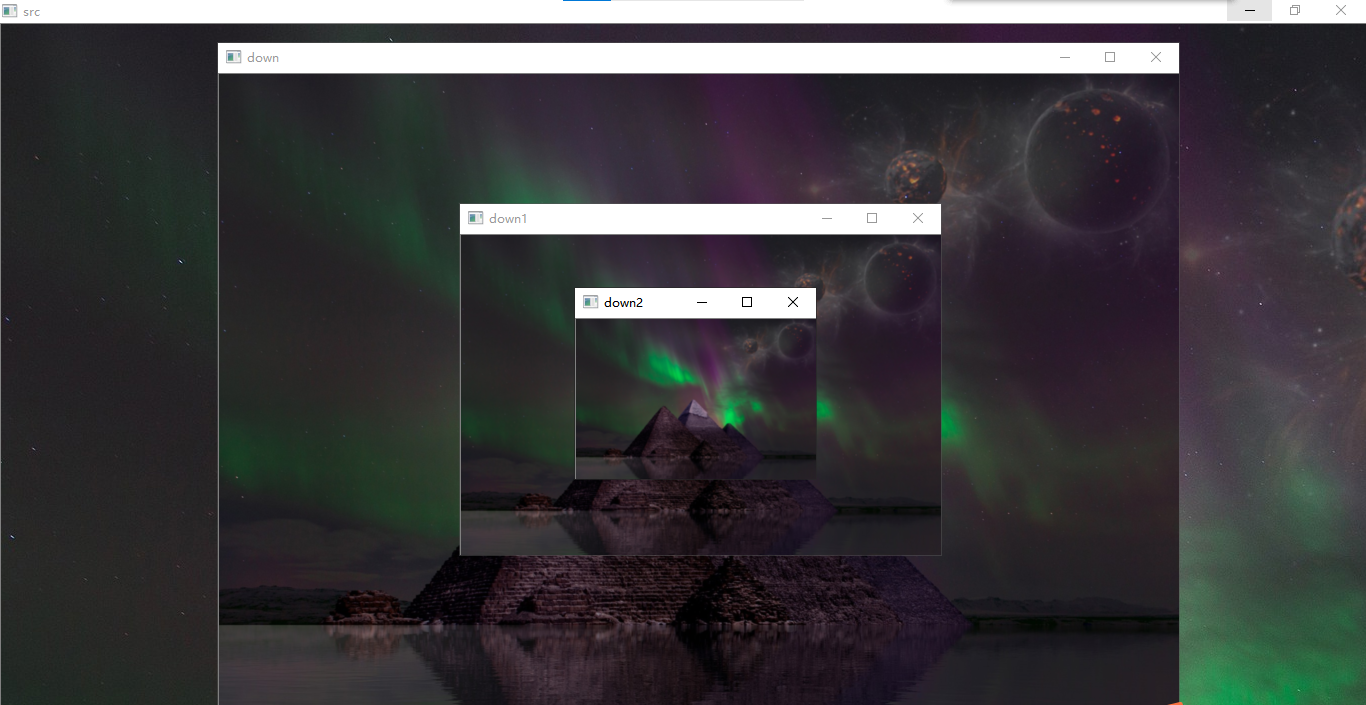
向上采样运行结果图，如下所示，明显可以发现图像已模糊

三、拉普拉斯金字塔

前面我们已经介绍过，一幅图像在经过向下采样后，再对其进行向上采样，是无法恢复为原始状态的。为了在向上采样时能够恢复具有较高分辨率的原始图像，就要获取在采样过程中所丢失的信息，这些丢失的信息就构成了拉普拉斯金字塔。

拉普拉斯金字塔的定义形式为：

L i = G i − p y r U p ( G i + 1 ) Li = Gi - pyrUp(Gi + 1) Li=Gi−pyrUp(Gi+1)

• L i L_i Li 表示拉普拉斯金字塔中的第 i 层。

• G i G_i Gi 表示高斯金字塔中的第 i 层。

• G i G_i Gi+1 表示高斯金字塔中的第 i+1 层。

拉普拉斯金字塔中的第 i 层 ，等于"高斯金字塔中的第 i 层"与"高斯金字塔中的第 i+1 层的向上采样结果"之差。如下图所示，展示了高斯金字塔和拉普拉斯金字塔的对应关系。

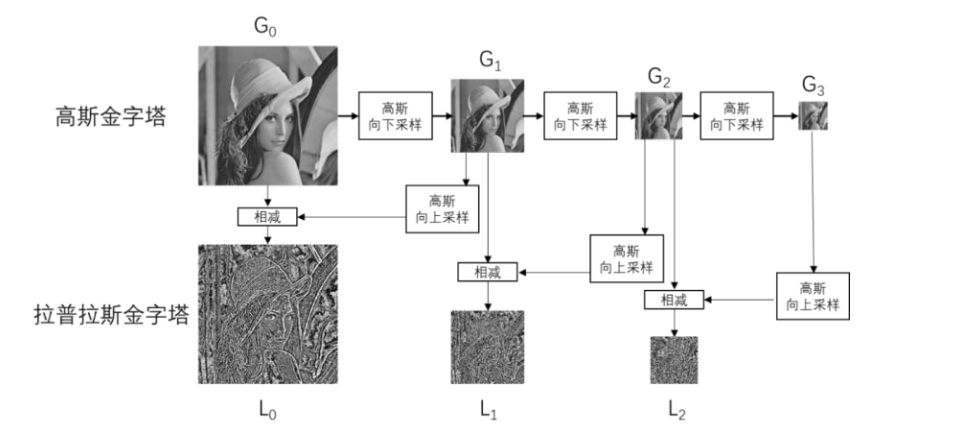
可以发现，先下采样，后上采样，丢失了很多细节（下采样和上采样不是可逆的，而上采样是病态多解问题）。那么同分辨率相减，多层叠加起来就是拉普拉斯金字塔！

可以发现，不同尺度下关注的细节是不一样的！如下图，将最小分辨率和最高分辨率的拉普拉斯图同尺度比较，可以发现，低分辨率关注的是接近于 base 的基础纹理（大纹理），而高分辨率下关注的细节是更精细的纹理（小纹理）

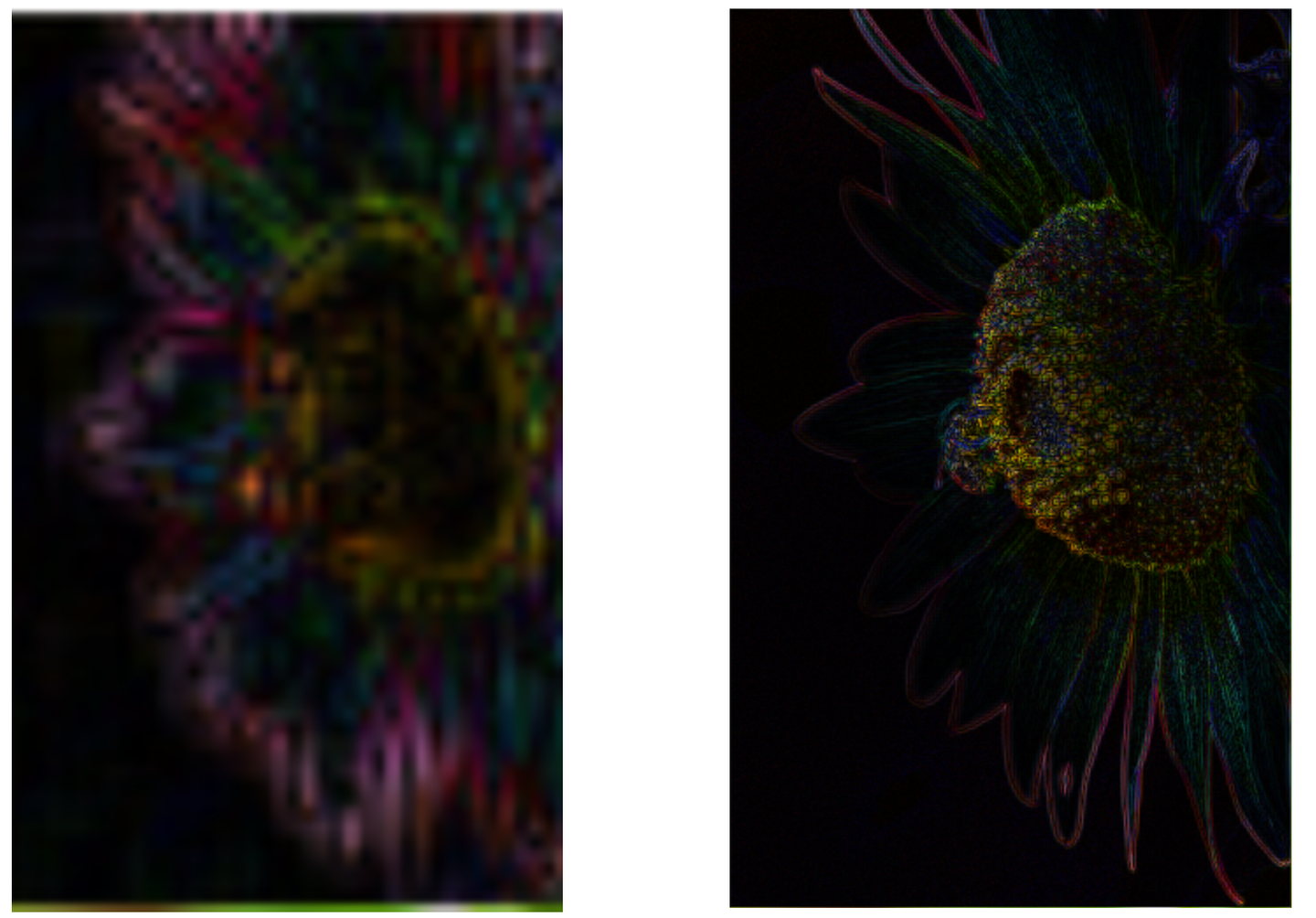
为了显示更清楚，灰度值 x 2

建立拉普拉斯金字塔的代码如下：

有一些小细节，例如，存储拉普拉斯结果的数据类型是 short，可表示 -32767 ~ 32767 之间，而图像一般是以8位 unsigned char 存储，范围 0 ~ 255，因此图像相减的值取值在 -255 ~ 255 之间，short 足够存储这个残差值（int 就太浪费了，精度也不会更高，毕竟后面用于压缩，能省一点是一点；char 只能表示 0~128；unsigned short 不能表示负数）。

using res_type = short;

std::vector< std::vector<res_type> > build_laplace_pyramid(const std::vector<cv::Mat>& gaussi_pyramid) {
    // 查看几层
    const int layers_num = gaussi_pyramid.size();
    // 准备一个结果
    std::vector< std::vector<res_type> > laplace_pyramid;
    laplace_pyramid.reserve(layers_num - 1);
    // 从低分辨率开始构建拉普拉斯金字塔
    for(int i = layers_num - 1; i >= 1; --i) {
        // 首先低分辨率先上采样到两倍大小
        cv::Mat upsampled = pyramid_upsample(gaussi_pyramid[i]);
        // 填补值，没用高斯
        pyramid_upsample_interpolate(upsampled);
        // 放到拉普拉斯金字塔
        const int length = upsampled.rows * upsampled.cols * upsampled.channels();
        std::vector<res_type> residual(length, 0);
        for(int k = 0;k < length; ++k)
            residual[k] = gaussi_pyramid[i - 1].data[k] - upsampled.data[k];
        laplace_pyramid.emplace_back(residual);
    }
    std::reverse(laplace_pyramid.begin(), laplace_pyramid.end());
    return laplace_pyramid;
}

四、重构

拉普拉斯金字塔的作用在于，能够恢复高分辨率的图像。下图演示了如何通过拉普拉斯金字塔恢复高分辨率图像。其中，右图是对左图的简化。

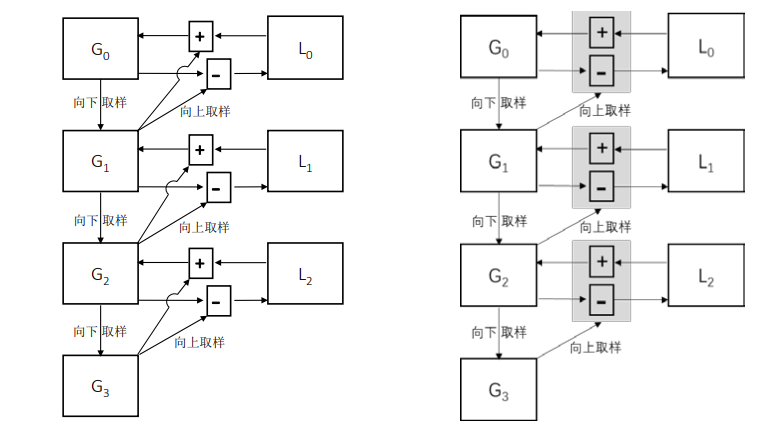
上图中各个标记的含义如下：

• G 0 、 G 1 、 G 2 、 G 3 G_0、G_1、G_2、G_3 G0、G1、G2、G3分别是高斯金字塔的第 0 层、第 1 层、第 2 层、第 3 层。
• L 0 、 L 1 、 L 2 L_0、L_1、L_2 L0、L1、L2分别是拉普拉斯金字塔的第 0 层、第 1 层、第 2 层。
• 向下的箭头表示向下采样操作（对应 cv2.pyrDown()函数）。
• 向右上方的箭头表示向上采样操作（对应 cv2.pyrUp()函数）。
• 加号"+"表示加法操作。
• 减号"-"表示减法操作

拉普拉斯金字塔恢复高分辨率图像的步骤：
 
1. 向下采样（高斯金字塔的构成）
G1=cv2.pyrDown(G0)
G2=cv2.pyrDown(G1)
G3=cv2.pyrDown(G2)
 
2. 拉普拉斯金字塔
L0=G0-cv2.pyrUp(G1)
L1=G1-cv2.pyrUp(G2)
L2=G2-cv2.pyrUp(G3)
 
3. 向上采样恢复高分辨率图像
G0=L0+cv2.pyrUp(G1)
G1=L1+cv2.pyrUp(G2)
​​​​​​​G2=L2+cv2.pyrUp(G3) 
 
虽然是简单的相加减关系，但是可以此过程的中间操作图像，进行创新

实际效果也确实还可以，增强了不少细节

为了显示清楚，细节 x2。并且，每个尺度下重构的图像都是无损还原！

全部代码

import cv2
 
src = cv2.imread("pyramid.jpg")
 
# 向下采样
down0 = cv2.pyrDown(src)
down1 = cv2.pyrDown(down0)
down2 = cv2.pyrDown(down1)
print("逐个向下采样后的图像尺寸：", "\n", src.shape, "\n", down0.shape, "\n", down1.shape, "\n", down2.shape)
 
# 向上采样
up2 = cv2.pyrUp(down2)
up1 = cv2.pyrUp(up2)
up0 = cv2.pyrUp(up1)
print("逐个向上采样后的图像尺寸：", "\n", up2.shape, "\n", up1.shape, "\n", up0.shape)
 
# 拉普拉斯变换(原理)
L0 = down0 - cv2.pyrUp(down1)
L1 = down1 - cv2.pyrUp(down2)
print("拉普拉斯变换后的图像尺寸：", "\n", L0.shape, "\n", L1.shape)
 
# 拉普拉斯变换(恢复原始图像)
src_L0 = L0 + cv2.pyrUp(down1)
src_L1 = L1 + cv2.pyrUp(down2)
print("拉普拉斯变换恢复的图像尺寸：", "\n", src_L0.shape, "\n", src_L1.shape)
 
cv2.imshow("src", src)
cv2.imshow("down", down0)
cv2.imshow("down1", down1)
cv2.imshow("down2", down2)
cv2.waitKey(0)
cv2.destroyAllWindows()
 
cv2.imshow("up2", up2)
cv2.imshow("up1", up1)
cv2.imshow("up", up0)
cv2.waitKey(0)
cv2.destroyAllWindows()
 
cv2.imshow("L0", L0)
cv2.imshow("L1", L1)
cv2.waitKey(0)
cv2.destroyAllWindows()
 
cv2.imshow("src_L0", src_L0)
cv2.imshow("src_L1", src_L1)
cv2.waitKey(0)
cv2.destroyAllWindows()

五、图像压缩

前面知道，拉普拉斯金字塔分解和重构，输入什么，输出的就是输入，并没有什么意思，但是这对于压缩而言，具有意义。从分解到重构是无损失的，那如果有损失呢？每个尺度下都损失一部分不重要的分量，保留主要分量，然后按照拉普拉斯金字塔重构，得到的结果虽然是有损的，但变化不大，且由于去除了一部分不重要的分量，存储上可以做优化。

那去掉哪一部分呢？

图像中 base 低频分量占主要部分，是图像的主要内容，但由于重构只需要最低分辨率下的小图，这一部分存储占的比例很小。图像中 detail 高频分量是占少数的，在这里就是多尺度下的拉普拉斯金字塔，但通过观察发现，每个尺度下的细节是很少的，如下，我们真正需要保存的就是细节中的更高频分量，那些接近于 0 的细节可以剔除！

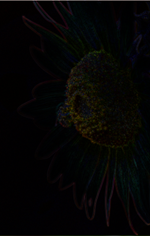
最高分辨率时的细节

下图是阈值为 6 时，每个尺度的拉普拉斯金字塔保留的点的比例，和信息损失，可见，在高分辨率下，PSNR 可以达到 41.5db，肉眼上其实看不大出来

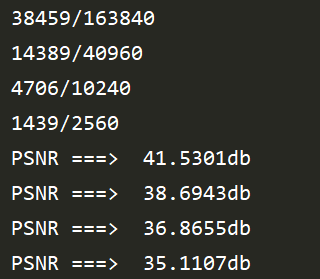
分辨率从高到低

压缩前后的对比；右侧是细节对比

可以发现，虽然整体内容上看不大出来区别，但细节上确实有一定损失的，而且因为根据阈值筛选是全局的操作，因此不保证之前的弱边缘还能保持连续。

以上是对图像信息的压缩，那如果是存储呢？根据 laplace 金字塔压缩信息的特点，对有损图像进行存储优化，实际需要保存的信息就是

• 低分辨率小图
• laplace 金字塔每一层中，大于某个阈值的点坐标，以及这个点在多个通道上的灰度值 实际表现，图像分辨率 520x320，金字塔层数5，阈值 6

实际表现，图像分辨率 520x320，金字塔层数 5，阈值 6

初次压缩的效果

reconstructed 是无损存储，compressed 是有损存储，压缩之后所需空间非但没有降低，还增大了！

如果增加金字塔的层数，毕竟尺度越大的高频细节越稀疏，同时提高阈值，过滤更多的无关细节，分辨率 4224x2886，金字塔层数 7，阈值 20，效果如下：

laplace_compressed: 经过拉普拉斯压缩后的图片，以 opencv 的 png 保存的结果；

laplace_reconstructed: 没有压缩的图片，包含了原图高分辨率的所有信息，opencv 的 png 保存；

compressed: 按照上面的存储格式，实际存储的结果，只存储了最低分辨率的结果以及压缩之后的拉普拉斯金字塔信息；

reconstructed: 没有压缩的图片，和 compressed 一样存储成二进制格式，存储宽、高、通道数目和图像内容等信息；

从上面可以看出几个初步结论：

• laplace_compressed 和 compressed 对比，34 MB VS 5MB，都是压缩的图像，前者是存储的原始分辨率的有损图像， 后者是只存储了按照 laplace金字塔和低分辨率图像写入的二进制文件，二者包含的图像信息是一样多的，但存储上确实有效，我上面的尝试是可行的！
• laplace_reconstructed 和 laplace_compressed 对比，前者无损，后者有损，但是直接用 OpenCV以 png 格式存储，二者所需存储一模一样，分辨率一样，还都是 unsigned char数据，因此在存储上没有任何优化，这也说明了上一条的必要性。
• laplace_reconstructed 和 reconstructed的存储所需空间很相近，说明宽、高、通道数目和图像内容足够描述原来的图像信息 。

但是由于压缩的太狠了，所以信息损失地有点多！重建的最高分辨率相比原图只有 35db。

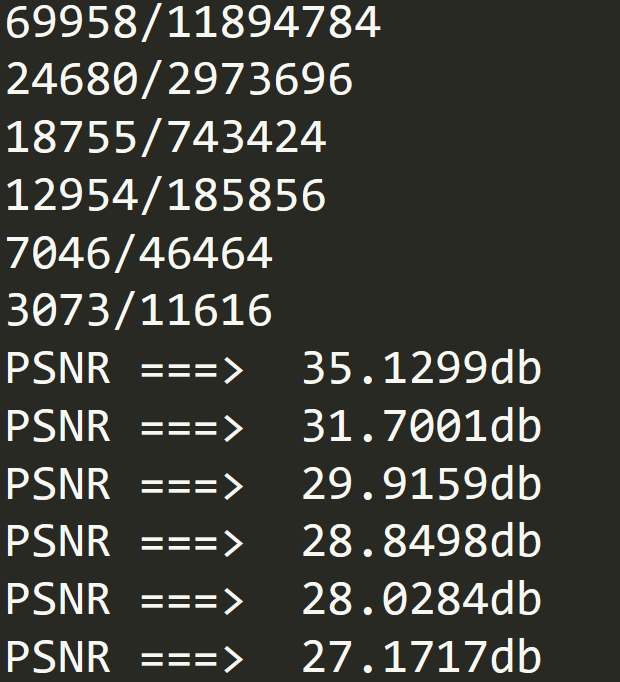
多尺度细节保留的点的比例，和对应信息损失

压缩之前

压缩之后

虽然效果不是很好，却是一次很好的实践！

六、图像融合

拼接

单纯从上面的 laplace 金字塔分解和重构，我是想不到还可以用于图像融合的。还是从一些博客中提到用来图像拼接之类的引用。

假设，现在有以下左右两幅图，我想把左图 L 的一半和右图 R 的一半拼接在一起

左图 L；右图 R

也就是按照下面的 mask 图，设为 M，输出 O = M ∗ L + ( 1 − M ) ∗ R O=M*L+(1-M)*R O=M∗L+(1−M)∗R

mask 图

直接拼在一起，可以得到下图

很明显，中间过渡的部分存在一条缝！因为左图和右图在亮度和颜色上都不同，怎么解决？

一个很直观的想法就是，把中间那条缝给模糊掉，比如使用高斯模糊等手段对 mask 图，使得左图右图交界处相互渗透，平滑灰度突变的结果，再将二者融合，灰度突变也许就不会这么明显了。

（为什么是对 mask 图做模糊，而不是对左图右图？因为要保留左图和右图的细节，不宜平滑二者细节，于是平滑 mask 图，对 mask 的平滑不影响原来的细节强弱）

直接实验

高斯模糊的半径为 2 时的结果

不大行，继续！

高斯模糊的半径为 14 时的结果

好像有点效果，缝隙减弱了很多，继续 ！

高斯模糊的半径为 30 时的结果

好像又更好了！缝隙已经不大看的出来了，但是二者亮度差还是有点大，加大力度！

高斯模糊的半径为 180 时的结果

高斯模糊的半径为 300 时的结果

我的天！现在缝隙已经消失了，而且从左边到右边的过渡也自然多了，完成任务！

虽然上面逐渐增强高斯模糊的力度，但是存在两个问题

• 这计算量太大了！高斯模糊的半径 300，高斯核大小 600x600，消耗太大了！
• 我们该如何确定，选多狠的高斯模糊是最合适的？

第一个问题------这就可以用到金字塔，构建多尺度，不必每次都增大高斯模糊的半径，降低分辨率可以近似"更大半径的高斯模糊"的效果。想象一下，有一张分辨率高分辨率图像，构建高斯金字塔，每个尺度下根据上面的方法，对当前尺度下的 mask 做高斯模糊，目的是平滑中间突变的部分，根据模糊后的 mask 拼接这个尺度的左图、右图，每个尺度下都可以得到一个拼接的结果，但实际上我们只需要最高分辨率时的拼接结果，如何结合那些更小分辨率的结果？

考虑这次的 laplace 金字塔，每个尺度下对那个尺度下的 mask 做模糊，但是拼接的不是各尺度的高斯金字塔的图像，拼接的是各尺度的 laplace 金字塔图像！融合的过程不变，改变的是低分辨率图和 laplace 金字塔

• 低分辨率由最小分辨率下左图、右图，根据同分辨率模糊的 mask 加权拼接得到；
• laplace 金字塔由每个尺度下左图、右图的 laplace 细节根据同分辨率下模糊的 mask 加权拼接得到。

根据这二者做 laplace 金字塔重建，这样从低分辨率到高分辨率重建就可以得到一张最高分辨率的图像，

发生了什么？每个尺度下其实都对不同尺度关注的细节做了 mask 平滑，低分辨率可以近似从远处观察的结果，低分辨率下 mask 平滑了拼接处的大纹理的过渡，近似于高分辨率下就是一大段的平滑效果...最高分辨率下的 mask 平滑的程度比较弱，处理的就是那些更小的纹理的过渡------这样多个尺度不断平滑，使得多个尺度的细节过渡都更自然，因此，最后得到的高分辨率结果就是过渡自然的结果。

第二个问题------选多狠的高斯模糊是最合适的呢，waiting...

根据上面的分析，对 laplace 做图像拼接的过程做个总结

步骤

1. 求左图、右图的高斯金字塔 G L G_L GL 、 G R G_R GR
2. 求左图、右图的 laplace 金字塔 L a p L Lap_{L} LapL 、 L a p R Lap_{R} LapR
3. 求 mask 图的高斯金字塔 G m a s k G_{mask} Gmask
4. 每个尺度（分辨率）下，根据当前尺度的 G m a s k G_{mask} Gmask拼接左、右图的 L a p L Lap_{L} LapL 、 L a p R Lap_{R} LapR ，最终得到拼接的laplace 金字塔 L a p f u s e d Lap_{fused} Lapfused
5. 生成最低分辨率的起始图------都选取最低分辨率下的 G L G_L GL 、 G R G_R GR ，根据同分辨率下的 G m a s k G_{mask} Gmask 进行拼接，得到最低分辨率下的拼接结果 O m i n O_{min} Omin
6. 从 O m i n O_{min} Omin开始，根据 L a p f u s e d Lap_{fused} Lapfused 构建得到最高分辨率的拼接结果。

直接实验：

3 层拉普拉斯金字塔的拼接结果

5 层拉普拉斯金字塔的拼接结果

8 层拉普拉斯金字塔的拼接结果

可以发现，随着拉普拉斯金字塔层数的增大，拼接的效果是越来越好的。这也近似于之前使用了更狠的高斯模糊。

虽然看起来效果还不错，但这是建立在左图右图"能"拼接的基础上，比如上面的例子，左图跟右图在拼接处是比较吻合的，没有一高一低的情况。因此基于 laplace 金字塔的图像拼接限制挺大的，对左图和右图匹配性有很高的要求，一般需要先经过配准。

参考资料：
图像处理基础（十）拉普拉斯金字塔、压缩、图像融合
你真正了解图像金字塔吗？详细介绍拉普拉斯金字塔和高斯金字塔（pyrDown() and pyrUp()），参考《OpenCV轻松入门：面向Python》

---

结~~~