作业:对心脏病数据集进行处理
在 Day25 的文章中,我们讨论了特征筛选(Feature Selection),即从原始特征中"挑选"出最有用的子集。今天我们进入数据预处理的另一个重要领域---降维(Dimensionality Reduction)。
与特征筛选不同,降维不是简单地丢弃特征,而是将原始的高维特征映射到一个低维空间中,生成全新的特征(Latent Features)。今天我们将通过心脏病数据集(Heart Disease Dataset),实战对比三种最常见的降维算法:PCA、t-SNE 和 LDA。
1. 为什么要降维?
在机器学习中,随着特征数量的增加,我们经常会遇到"维度灾难"(Curse of Dimensionality),导致模型过拟合或计算量爆炸。降维主要有以下目的:
压缩数据:减少计算量和存储空间。
去除噪声:丢弃次要的方差信息,保留主要信号。
可视化:将高维数据压扁到 2D 或 3D 以便人眼观察。
2.数据准备与基准模型
2.1数据加载与预处理
python
# Day26 常见的降维算法
#作业:对心脏病数据集进行处理
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import warnings
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.manifold import TSNE
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
import time
warnings.filterwarnings("ignore")
# 设置中文字体(解决中文显示问题)
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False
data = pd.read_csv("heart.csv")
# 处理分类变量(如有)
cat_cols = data.select_dtypes(include=["object"]).columns
if len(cat_cols) > 0:
data = pd.get_dummies(data, columns=cat_cols)
# 将 bool 转为 int
bool_cols = data.select_dtypes(include=["bool"]).columns
if len(bool_cols) > 0:
data[bool_cols] = data[bool_cols].astype(int)
# 数值列缺失值用众数填充
num_cols = data.select_dtypes(include=["number"]).columns
if len(num_cols) > 0:
data[num_cols] = data[num_cols].fillna(data[num_cols].mode().iloc[0])
# 如果存在 Id 列则删除
if "Id" in data.columns:
data.drop(columns=["Id"], inplace=True)
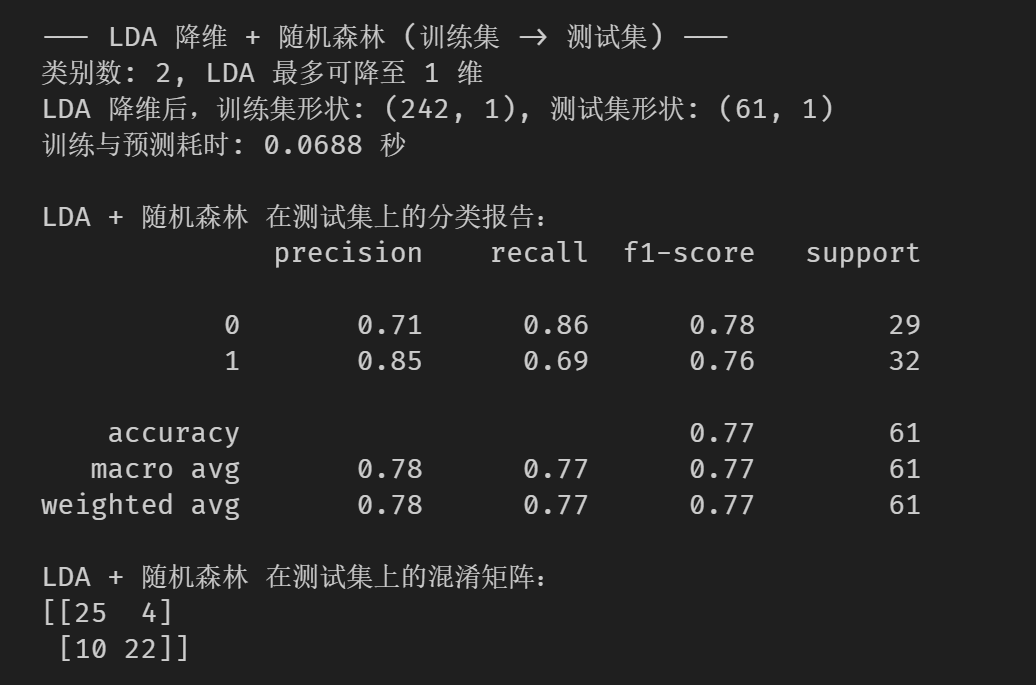
data.info()
# 划分特征和标签
X = data.drop(["target"], axis=1)
y = data["target"]
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)效果图
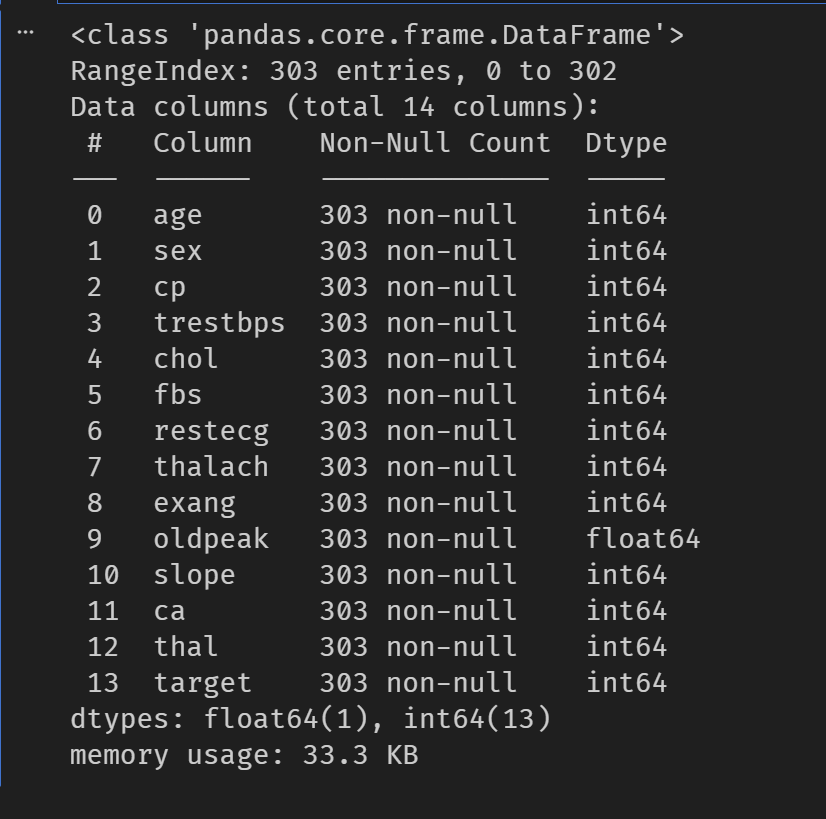
2.2默认随机森林(基准模型)
python
# 默认随机森林(基准模型)
print("--- 默认随机森林 (训练集 -> 测试集) ---")
start_time = time.time()
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train)
rf_pred = rf_model.predict(X_test)
end_time = time.time()
print(f"训练与预测耗时: {end_time - start_time:.4f} 秒")
print("\n默认随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred))
print("默认随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred))效果图
3. 算法一:主成分分析 (PCA)
原理:PCA(Principal Component Analysis)是一种无监督的线性降维方法。它的核心思想是找到数据方差最大的方向(主成分),将数据投影到这些方向上,从而尽可能多地保留原始信息。
我们尝试将数据降维,保留 95% 的方差:
python
# PCA + 随机森林(简洁版)
print("--- PCA 降维 + 随机森林 (训练集 -> 测试集) ---")
start_time = time.time()
# 步骤 1: 特征缩放
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)
# 步骤 2: PCA降维(保留95%方差)
pca = PCA(random_state=42)
pca.fit(X_train_scaled)
n_components_95 = np.argmax(np.cumsum(pca.explained_variance_ratio_) >= 0.95) + 1
print(f"为了保留95%的方差,需要的主成分数量: {n_components_95}")
pca = PCA(n_components=n_components_95, random_state=42)
X_train_pca = pca.fit_transform(X_train_scaled)
X_test_pca = pca.transform(X_test_scaled)
# 训练与评估
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train_pca, y_train)
pred = rf_model.predict(X_test_pca)
end_time = time.time()
print(f"训练与预测耗时: {end_time - start_time:.4f} 秒")
我们测试下降低到10维的效果
python
# 我们测试下降低到10维的效果
n_components_pca = 10
pca_manual = PCA(n_components=n_components_pca, random_state=42)
X_train_pca = pca_manual.fit_transform(X_train_scaled)
X_test_pca = pca_manual.transform(X_test_scaled) # 使用在训练集上fit的pca
print(f"PCA降维后,训练集形状: {X_train_pca.shape}, 测试集形状: {X_test_pca.shape}")
start_time_pca_manual = time.time()
# 步骤 3: 训练随机森林分类器
rf_model_pca = RandomForestClassifier(random_state=42)
rf_model_pca.fit(X_train_pca, y_train)
# 步骤 4: 在测试集上预测
rf_pred_pca_manual = rf_model_pca.predict(X_test_pca)
end_time_pca_manual = time.time()
print(f"手动PCA降维后,训练与预测耗时: {end_time_pca_manual - start_time_pca_manual:.4f} 秒")
print("\n手动 PCA + 随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred_pca_manual))
print("手动 PCA + 随机森林 在测试集上的混淆矩阵:")
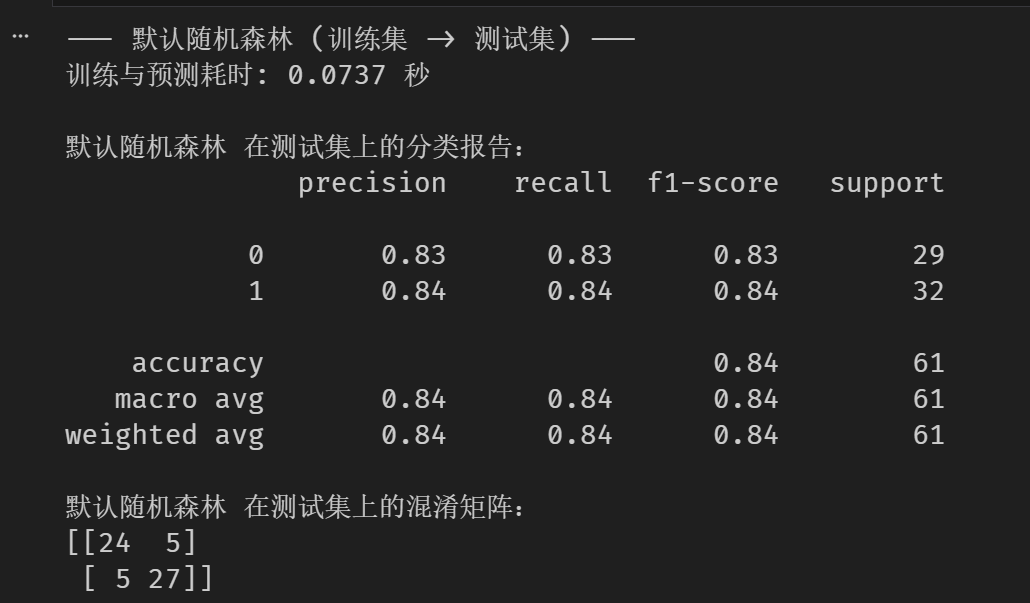
print(confusion_matrix(y_test, rf_pred_pca_manual))效果图:
分析 :PCA 将特征从 13 维降至 10 维后,准确率反而从 84% 微升至 85%。这说明原始数据中包含了一定的噪声或冗余信息,PCA 有效地提取了主要信号。
4. 算法二:t-SNE (t-Distributed Stochastic Neighbor Embedding)
原理:t-SNE 是一种非线性降维算法。与 PCA 不同,它主要关注保持数据的局部结构,非常适合将高维数据降维到 2D 或 3D 进行可视化。
注意 :t-SNE 计算量大,且通常不适合用于分类器的特征工程(因为它不能很好地保留全局距离,且对新样本的转换较困难)。让我们看看实战结果是否印证了这一点。
python
# t-SNE + 随机森林(简洁版)
print("\n--- t-SNE 降维 + 随机森林 (训练集 -> 测试集) ---")
print("注意: t-SNE 主要用于可视化,用于分类可能效果不佳\n")
# 步骤 1: 特征缩放
scaler_tsne = StandardScaler()
X_train_scaled_tsne = scaler_tsne.fit_transform(X_train)
X_test_scaled_tsne = scaler_tsne.transform(X_test)
# 步骤 2: t-SNE 降维(降至2维)
n_components_tsne = 2
print(f"正在对训练集进行 t-SNE 降维至 {n_components_tsne} 维...")
start_tsne_train = time.time()
tsne_train = TSNE(
n_components=n_components_tsne,
perplexity=30,
n_iter=1000,
init='pca',
learning_rate='auto',
random_state=42,
n_jobs=-1
)
X_train_tsne = tsne_train.fit_transform(X_train_scaled_tsne)
end_tsne_train = time.time()
print(f"训练集 t-SNE 完成,耗时: {end_tsne_train - start_tsne_train:.2f} 秒")
print(f"正在对测试集进行 t-SNE 降维至 {n_components_tsne} 维...")
start_tsne_test = time.time()
tsne_test = TSNE(
n_components=n_components_tsne,
perplexity=30,
n_iter=1000,
init='pca',
learning_rate='auto',
random_state=42,
n_jobs=-1
)
X_test_tsne = tsne_test.fit_transform(X_test_scaled_tsne)
end_tsne_test = time.time()
print(f"测试集 t-SNE 完成,耗时: {end_tsne_test - start_tsne_test:.2f} 秒")
print(f"t-SNE 降维后,训练集形状: {X_train_tsne.shape}, 测试集形状: {X_test_tsne.shape}")
# 步骤 3: 训练与评估
start_rf = time.time()
rf_model_tsne = RandomForestClassifier(random_state=42)
rf_model_tsne.fit(X_train_tsne, y_train)
rf_pred_tsne = rf_model_tsne.predict(X_test_tsne)
end_rf = time.time()
print(f"随机森林训练与预测耗时: {end_rf - start_rf:.4f} 秒")
total_time = (end_tsne_train - start_tsne_train) + (end_tsne_test - start_tsne_test) + (end_rf - start_rf)
print(f"t-SNE 总耗时(包括两次降维和RF): {total_time:.2f} 秒")
print("\nt-SNE + 随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred_tsne))
print("t-SNE + 随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred_tsne))效果图
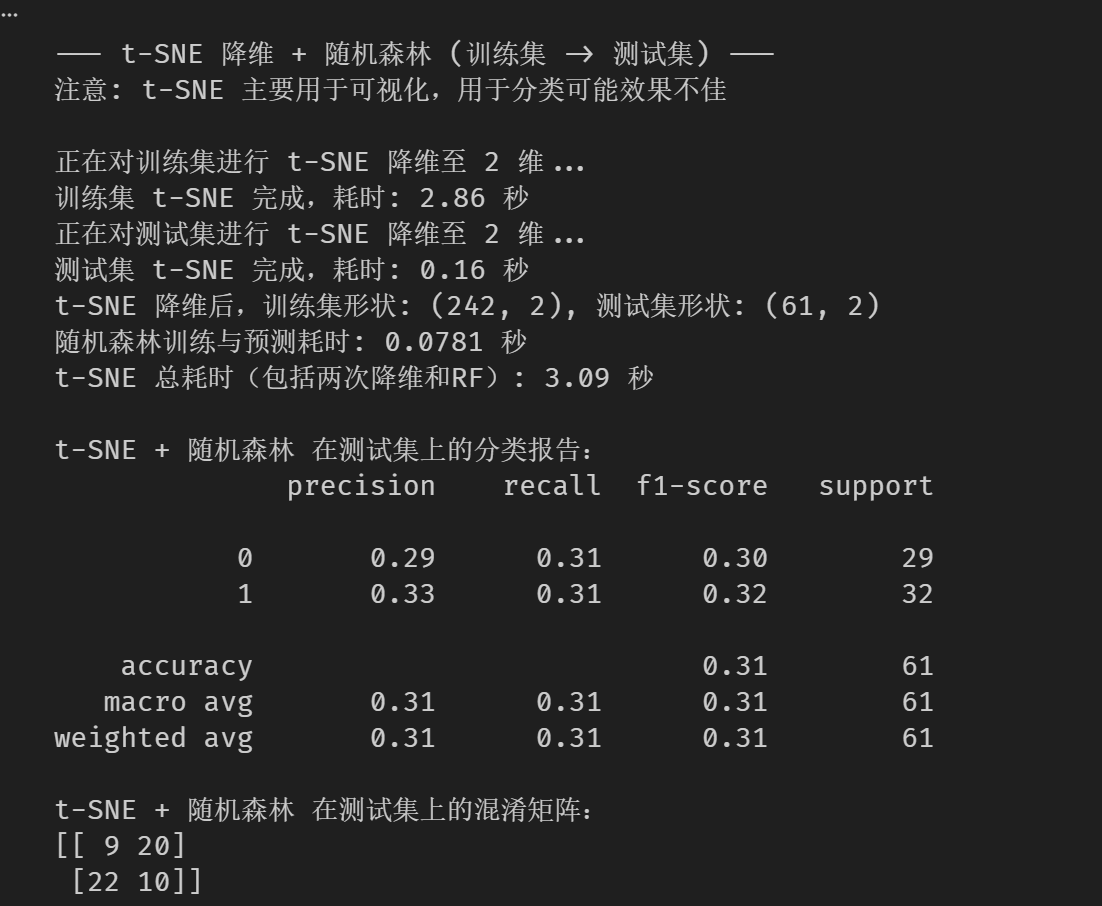
分析 :惨败 。准确率仅为 31%.
原因:
非参数化映射:t-SNE 学习的是样本间的概率分布,而不是一个通用的投影函数,因此很难将测试集"正确地"映射到与训练集相同的空间中。
目标不同:t-SNE 是为了"好看"(可视化聚类),而不是为了"好分"(分类边界清晰)。
结论 :永远不要直接把 t-SNE 的结果喂给分类器,请只用它来画图。
5. 算法三:线性判别分析 (LDA)
原理:LDA(Linear Discriminant Analysis)是一种有监督的降维方法。与 PCA 寻找"最大方差"不同,LDA 寻找的是"最大化类间距离,最小化类内距离"的方向。它天生就是为了分类而生的。
限制:LDA 降维后的最大维度是K-1(K为类别数)因为我们是二分类问题(有病/没病),LDA 只能降到 1维。
python
# LDA + 随机森林
print("\n--- LDA 降维 + 随机森林 (训练集 -> 测试集) ---")
# 步骤 1: 特征缩放
scaler_lda = StandardScaler()
X_train_scaled_lda = scaler_lda.fit_transform(X_train)
X_test_scaled_lda = scaler_lda.transform(X_test)
# 步骤 2: 计算 LDA 最大降维维度
n_classes = y_train.nunique() if hasattr(y_train, 'nunique') else len(np.unique(y_train))
max_lda_components = min(X_train_scaled_lda.shape[1], n_classes - 1)
print(f"类别数: {n_classes}, LDA 最多可降至 {max_lda_components} 维")
# 步骤 3: LDA 降维
lda = LDA(n_components=max_lda_components, solver='svd')
X_train_lda = lda.fit_transform(X_train_scaled_lda, y_train)
X_test_lda = lda.transform(X_test_scaled_lda)
print(f"LDA 降维后,训练集形状: {X_train_lda.shape}, 测试集形状: {X_test_lda.shape}")
# 步骤 4: 训练与评估
start_time = time.time()
rf_model_lda = RandomForestClassifier(random_state=42)
rf_model_lda.fit(X_train_lda, y_train)
rf_pred_lda = rf_model_lda.predict(X_test_lda)
end_time = time.time()
print(f"训练与预测耗时: {end_time - start_time:.4f} 秒")
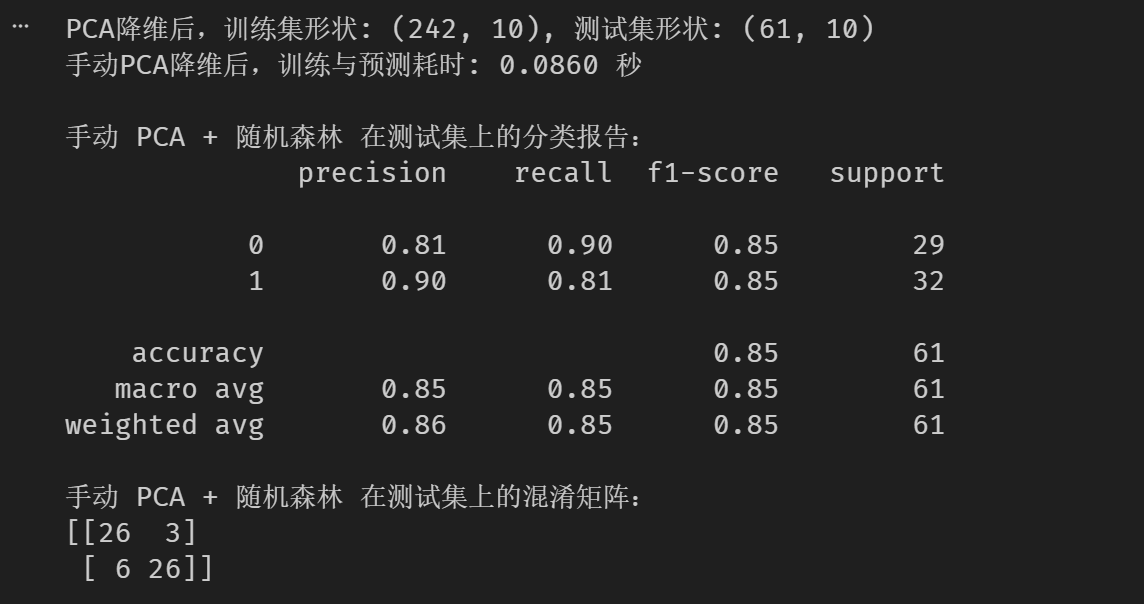
print("\nLDA + 随机森林 在测试集上的分类报告:")
print(classification_report(y_test, rf_pred_lda))
print("LDA + 随机森林 在测试集上的混淆矩阵:")
print(confusion_matrix(y_test, rf_pred_lda))效果图: