倒立摆模型
1. 系统描述与建模假设
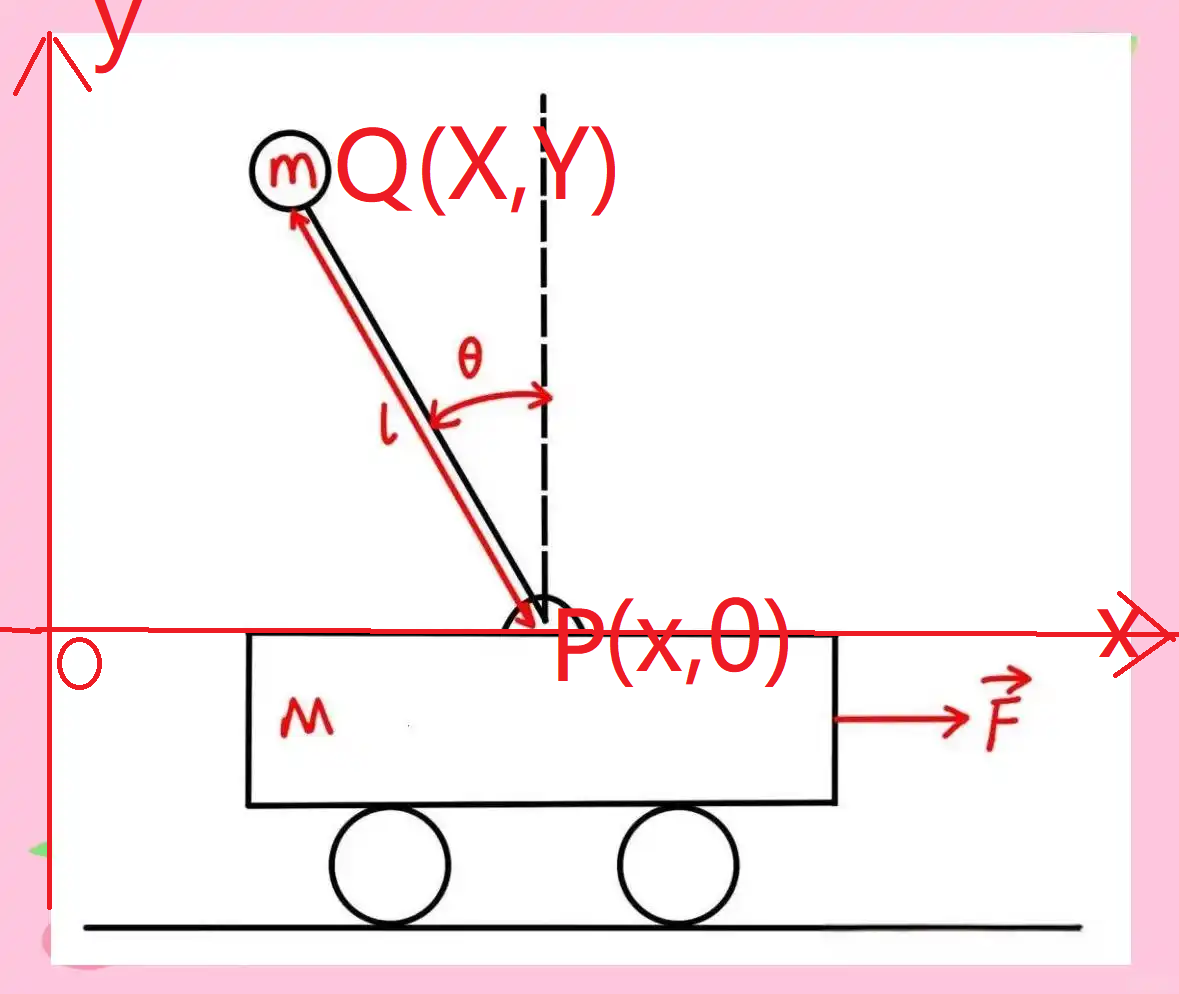
1.1 系统结构
- 小车质量: M M M,沿水平方向运动
- 摆杆长度: l l l,刚性杆,质量忽略
- 摆端小球质量: m m m
- 摆轴位置 P ( x , 0 ) P(x,0) P(x,0)
- 摆轴旋转角度 θ \theta θ
- 摆端小球位置: Q ( X , Y ) Q(X,Y) Q(X,Y)
- 小车受水平控制力: F F F
目标:通过控制小车水平控制力 F F F ,使摆杆稳定在倒立位置。
1.2 广义坐标选取
选取如下广义坐标:
- x x x:小车的水平位移
- θ \theta θ:摆杆相对于竖直向上方向的夹角(逆时针为正)
约定倒立平衡点为:
θ = 0 \theta = 0 θ=0
2. 运动学关系
2.1 摆球位置
摆球在惯性坐标系中的位置为:
X = x − l sin θ Y = l cos θ \begin{aligned} X &= x - l\sin\theta \\ Y &= l\cos\theta \end{aligned} XY=x−lsinθ=lcosθ
2.2 速度表达式
对时间求导:
X ˙ = x ˙ − l θ ˙ cos θ Y ˙ = − l θ ˙ sin θ \begin{aligned} \dot X &= \dot x - l\dot\theta\cos\theta \\ \dot Y &= -l\dot\theta\sin\theta \end{aligned} X˙Y˙=x˙−lθ˙cosθ=−lθ˙sinθ
速度平方为:
v 2 = X ˙ 2 + Y ˙ 2 = x ˙ 2 − 2 l x ˙ θ ˙ cos θ + l 2 θ ˙ 2 \begin{aligned} v^2 &= \dot X^2 + \dot Y^2 \\ &= \dot x^2 - 2l\dot x\dot\theta\cos\theta + l^2\dot\theta^2 \end{aligned} v2=X˙2+Y˙2=x˙2−2lx˙θ˙cosθ+l2θ˙2
3. 能量表达式
3.1 动能 T T T
小车的动能:
T cart = 1 2 M x ˙ 2 T_{\text{cart}} = \frac{1}{2} M \dot x^2 Tcart=21Mx˙2
摆球的动能:
T pend = 1 2 m v 2 T_{\text{pend}} = \frac{1}{2} m v^2 Tpend=21mv2
系统总动能:
T = 1 2 ( M + m ) x ˙ 2 − m l x ˙ θ ˙ cos θ + 1 2 m l 2 θ ˙ 2 T=\frac{1}{2}(M+m)\dot x^2- ml\dot x\dot\theta\cos\theta+ \frac{1}{2}ml^2\dot\theta^2 T=21(M+m)x˙2−mlx˙θ˙cosθ+21ml2θ˙2
3.2 势能 V V V
以小车铰点高度为零势能参考:
V = m g l cos θ V = m g l \cos\theta V=mglcosθ
倒立位置 θ = 0 \theta = 0 θ=0 对应势能最大值,是一个不稳定平衡点。
4. 拉格朗日函数
拉格朗日量定义为:
L = T − V \mathcal{L} = T - V L=T−V
代入得:
L = 1 2 ( M + m ) x ˙ 2 − m l x ˙ θ ˙ cos θ + 1 2 m l 2 θ ˙ 2 − m g l cos θ \mathcal{L}=\frac{1}{2}(M+m)\dot x^2- ml\dot x\dot\theta\cos\theta+ \frac{1}{2}ml^2\dot\theta^2- mgl\cos\theta L=21(M+m)x˙2−mlx˙θ˙cosθ+21ml2θ˙2−mglcosθ
5. 拉格朗日方程
拉格朗日方程为:
d d t ( ∂ L ∂ q ˙ i ) − ∂ L ∂ q i = Q i \frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial \dot q_i}\right)-\frac{\partial \mathcal{L}}{\partial q_i}= Q_i dtd(∂q˙i∂L)−∂qi∂L=Qi
其中广义力为:
- Q x = F Q_x = F Qx=F
- Q θ = 0 Q_\theta = 0 Qθ=0
5.1 关于 x x x 的方程
( M + m ) x ¨ − m l ( θ ¨ cos θ − θ ˙ 2 sin θ ) = F (M+m)\ddot x- ml(\ddot\theta\cos\theta - \dot\theta^2\sin\theta)= F (M+m)x¨−ml(θ¨cosθ−θ˙2sinθ)=F
5.2 关于 θ \theta θ 的方程
− m l x ¨ cos θ + m l 2 θ ¨ − m g l sin θ = 0 -ml\ddot x\cos\theta+ ml^2\ddot\theta- mgl\sin\theta= 0 −mlx¨cosθ+ml2θ¨−mglsinθ=0
5.3 完整非线性动力学模型
{ ( M + m ) x ¨ − m l θ ¨ cos θ + m l θ ˙ 2 sin θ = F m l 2 θ ¨ − m l x ¨ cos θ − m g l sin θ = 0 \begin{cases} (M+m)\ddot x - ml\ddot\theta\cos\theta + ml\dot\theta^2\sin\theta = F \\ ml^2\ddot\theta-ml\ddot x\cos\theta -mgl\sin\theta = 0 \end{cases} {(M+m)x¨−mlθ¨cosθ+mlθ˙2sinθ=Fml2θ¨−mlx¨cosθ−mglsinθ=0
6. 平衡点与线性化
6.1 倒立平衡点
θ = 0 , θ ˙ = 0 , x ˙ = 0 \theta = 0,\quad \dot\theta = 0,\quad \dot x = 0 θ=0,θ˙=0,x˙=0
小角度近似:
sin θ ≈ θ , cos θ ≈ 1 \sin\theta \approx \theta,\qquad \cos\theta \approx 1 sinθ≈θ,cosθ≈1
6.2 线性化方程
{ ( M + m ) x ¨ − m l θ ¨ = F − m l x ¨ + m l 2 θ ¨ = m g l θ \begin{cases} (M+m)\ddot x - ml\ddot\theta = F \\ -ml\ddot x+ml^2\ddot\theta= mgl\theta \end{cases} {(M+m)x¨−mlθ¨=F−mlx¨+ml2θ¨=mglθ
7. 状态空间表示
M + m − m l − m l m l 2 \] \[ x ¨ θ ¨ \] = \[ F m g l θ \] \\begin{bmatrix} M+m \& -ml \\\\ -ml \& ml\^2 \\end{bmatrix} \\begin{bmatrix} \\ddot x \\\\ \\ddot\\theta \\end{bmatrix} = \\begin{bmatrix} F \\\\ mgl\\,\\theta \\end{bmatrix} \[M+m−ml−mlml2\]\[x¨θ¨\]=\[Fmglθ
定义状态向量为:
x = [ x x ˙ θ θ ˙ ] \mathbf{x} = \begin{bmatrix} x \\ \dot x \\ \theta \\ \dot\theta \end{bmatrix} x= xx˙θθ˙
控制输入为:
u = F u = F u=F
则系统的状态空间模型可写为:
x ˙ = [ 0 1 0 0 0 0 m g M 0 0 0 0 1 0 0 ( M + m ) g M l 0 ] x + [ 0 1 M 0 1 M l ] u \dot{\mathbf{x}} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{mg}{M} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{(M+m)g}{Ml} & 0 \end{bmatrix} \mathbf{x} + \begin{bmatrix} 0 \\ \frac{1}{M} \\ 0 \\ \frac{1}{Ml} \end{bmatrix} u x˙= 000010000Mmg0Ml(M+m)g0010 x+ 0M10Ml1 u
8. 系统特性分析
8.1 稳定性分析
- 倒立位置是无控制下的 不稳定平衡点
- 系统矩阵 (A) 的特征值分析:
eig ( A ) = 特征值 \text{eig}(A) = \text{特征值} eig(A)=特征值
其中必有正实部 → 系统不稳定
8.2 可控性与可观性
- 可控性矩阵:
C = [ B , A B , A 2 B , A 3 B ] \mathcal{C} = [B, AB, A^2B, A^3B] C=[B,AB,A2B,A3B] - 可观性矩阵:
O = [ C C A C A 2 C A 3 ] \mathcal{O} = \begin{bmatrix} C \\ CA \\ CA^2 \\ CA^3 \end{bmatrix} O= CCACA2CA3 - 对倒立摆系统,可控且可观,意味着可以通过状态反馈实现稳定控制
9. 控制器设计
9.1 状态反馈控制
- 控制目标:选择状态反馈增益矩阵 (K),使闭环系统稳定
- 控制律:
u = − K x u = -K \mathbf{x} u=−Kx - 闭环系统:
x ˙ = ( A − B K ) x \dot{\mathbf{x}} = (A - BK)\mathbf{x} x˙=(A−BK)x
9.2 LQR 最优控制
- 代价函数:
J = ∫ 0 ∞ ( x T Q x + u T R u ) d t J = \int_0^\infty (\mathbf{x}^T Q \mathbf{x} + u^T R u)\, dt J=∫0∞(xTQx+uTRu)dt - 求解连续时间 Riccati 方程得到最优反馈增益:
K = R − 1 B T P K = R^{-1} B^T P K=R−1BTP
9.3 极点配置 (Pole Placement)
- 根据系统自然频率与阻尼比设计期望闭环极点
- 使用 MATLAB / Python 的
place或手工设计矩阵 (K)
10. 仿真与验证
- 使用 MATLAB / Simulink 仿真:
- 非线性模型 + 状态反馈
- 初始角度扰动:(\theta_0 \neq 0)
- 观察 ( θ \theta θ(t)) 收敛到 0,(x(t)) 平稳移动
- 控制力 (F(t)) 观察:
- 是否合理,避免过大饱和
- 可绘制曲线:
- θ ( t ) \theta(t) θ(t)
- x ( t ) x(t) x(t)
- 控制输入 ( t ) (t) (t)