从ZUFT光速螺旋运动求导推出自然常数e

一、ZUFT核心方程：空间的光速螺旋运动

1.1 基本方程

张祥前统一场论核心假设：空间本身以光速进行圆柱状螺旋运动

r ⃗ ( t ) = r cos ⁡ ( ω t ) i ^ + r sin ⁡ ( ω t ) j ^ + h t k ^ \vec{r}(t) = r\cos(\omega t)\hat{i} + r\sin(\omega t)\hat{j} + ht\hat{k} r (t)=rcos(ωt)i^+rsin(ωt)j^+htk^

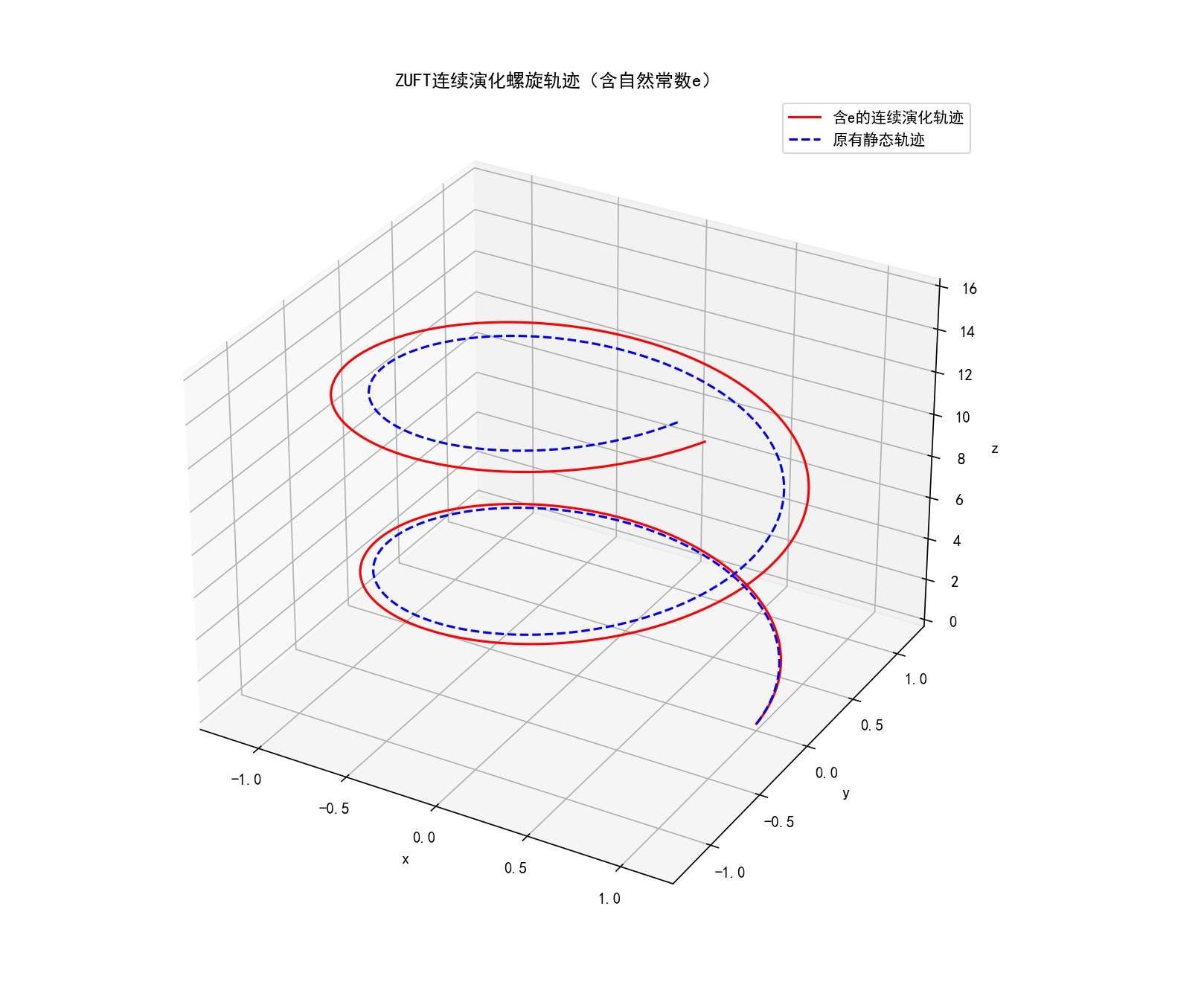
其中：

r r r = 螺旋半径（常数）
ω \omega ω = 角频率（常数）
h h h = 轴向速度（常数）
t t t = 时间参数

物理图像：

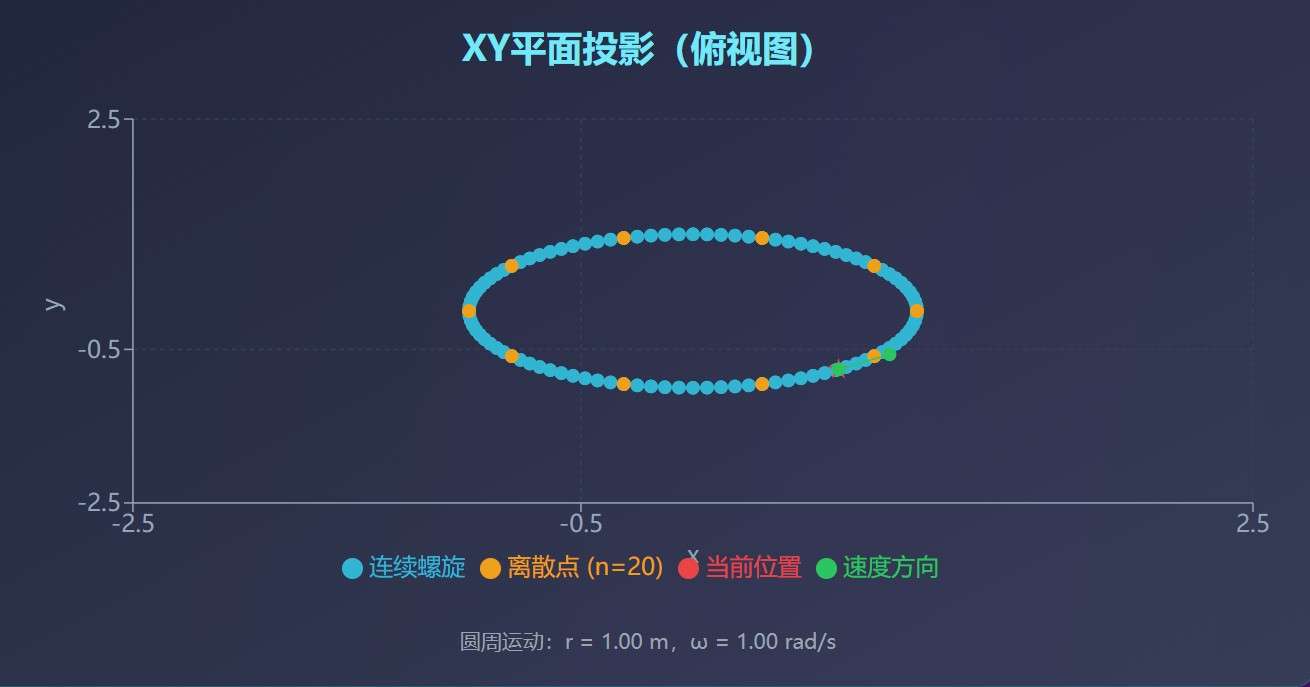
水平面（xy平面）：匀速圆周运动，半径r，角速度ω
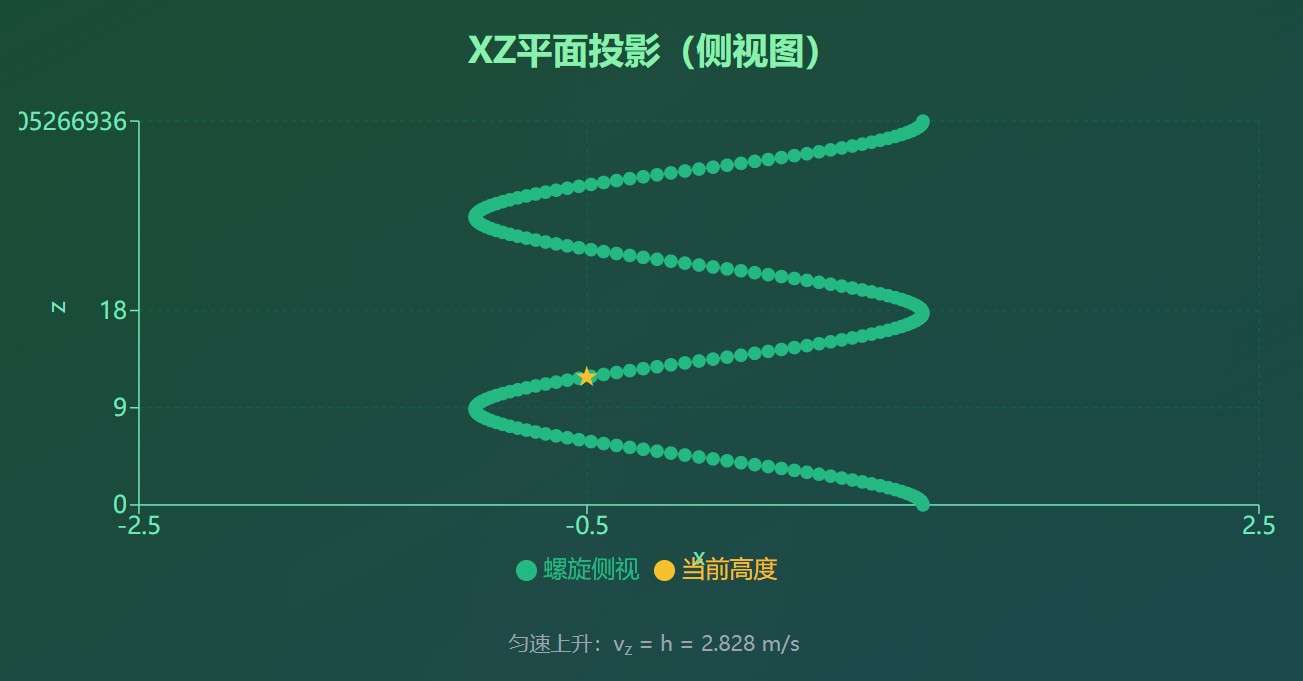
垂直方向（z轴）：匀速上升，速度h

1.2 光速约束条件

ZUFT核心约束：空间点的运动速度恒等于光速c

求一阶导数（速度）：
v ⃗ ( t ) = d r ⃗ d t = − r ω sin ⁡ ( ω t ) i ^ + r ω cos ⁡ ( ω t ) j ^ + h k ^ \vec{v}(t) = \frac{d\vec{r}}{dt} = -r\omega\sin(\omega t)\hat{i} + r\omega\cos(\omega t)\hat{j} + h\hat{k} v (t)=dtdr =−rωsin(ωt)i^+rωcos(ωt)j^+hk^

速度模长：
∣ v ⃗ ∣ = ( − r ω sin ⁡ ω t ) 2 + ( r ω cos ⁡ ω t ) 2 + h 2 |\vec{v}| = \sqrt{(-r\omega\sin\omega t)^2 + (r\omega\cos\omega t)^2 + h^2} ∣v ∣=(−rωsinωt)2+(rωcosωt)2+h2

= r 2 ω 2 ( sin ⁡ 2 ω t + cos ⁡ 2 ω t ) + h 2 = \sqrt{r^2\omega^2(\sin^2\omega t + \cos^2\omega t) + h^2} =r2ω2(sin2ωt+cos2ωt)+h2

= r 2 ω 2 + h 2 = \sqrt{r^2\omega^2 + h^2} =r2ω2+h2

光速约束 要求：
r 2 ω 2 + h 2 = c \boxed{\sqrt{r^2\omega^2 + h^2} = c} r2ω2+h2 =c

即：
r 2 ω 2 + h 2 = c 2 （螺旋参数约束方程） r^2\omega^2 + h^2 = c^2 \quad \text{（螺旋参数约束方程）} r2ω2+h2=c2（螺旋参数约束方程）

物理意义：

切向速度： v t = r ω v_t = r\omega vt=rω（圆周运动）
轴向速度： v z = h v_z = h vz=h（垂直上升）
总速度： v t 2 + v z 2 = c \sqrt{v_t^2 + v_z^2} = c vt2+vz2 =c（光速）

二、复数表示：自然常数e的第一次出现

2.1 水平分量的复数化

将螺旋运动的水平投影表示为复数：

z ( t ) = x ( t ) + i y ( t ) = r cos ⁡ ( ω t ) + i r sin ⁡ ( ω t ) z(t) = x(t) + iy(t) = r\cos(\omega t) + ir\sin(\omega t) z(t)=x(t)+iy(t)=rcos(ωt)+irsin(ωt)

利用欧拉公式 ：
e i θ = cos ⁡ θ + i sin ⁡ θ e^{i\theta} = \cos\theta + i\sin\theta eiθ=cosθ+isinθ

得到：
z ( t ) = r e i ω t \boxed{z(t) = re^{i\omega t}} z(t)=reiωt

这是自然常数e的第一次直接出现！

完整的三维螺旋运动可写为：
r ⃗ ( t ) = Re ( r e i ω t ) i ^ + Im ( r e i ω t ) j ^ + h t k ^ \vec{r}(t) = \text{Re}(re^{i\omega t})\hat{i} + \text{Im}(re^{i\omega t})\hat{j} + ht\hat{k} r (t)=Re(reiωt)i^+Im(reiωt)j^+htk^

或用复矢量记号：
r ⃗ ( t ) = r e i ω t e ^ ⊥ + h t k ^ \vec{r}(t) = re^{i\omega t}\hat{e}_\perp + ht\hat{k} r (t)=reiωte^⊥+htk^

其中 e ^ ⊥ \hat{e}_\perp e^⊥ 是水平面的复单位矢量。

2.2 速度的复数表示

对复数位置求导：
d z d t = d d t ( r e i ω t ) = r ⋅ i ω ⋅ e i ω t = i ω z ( t ) \frac{dz}{dt} = \frac{d}{dt}(re^{i\omega t}) = r \cdot i\omega \cdot e^{i\omega t} = i\omega z(t) dtdz=dtd(reiωt)=r⋅iω⋅eiωt=iωz(t)

关键性质 ：复数速度与复数位置成正比，比例系数为 i ω i\omega iω

这表明：
d z d t = i ω z ⇒ z ( t ) = z 0 e i ω t \frac{dz}{dt} = i\omega z \quad \Rightarrow \quad z(t) = z_0 e^{i\omega t} dtdz=iωz⇒z(t)=z0eiωt

物理意义：旋转运动的数学本质是复指数演化！

三、求导推导：从离散相位到连续指数

3.1 离散相位增量

将时间区间 [ 0 , T ] [0, T] [0,T] 分成 n n n 个离散步长：
Δ t = T n \Delta t = \frac{T}{n} Δt=nT

每个离散时刻： t k = k Δ t t_k = k\Delta t tk=kΔt， k = 0 , 1 , 2 , ... , n k = 0, 1, 2, \ldots, n k=0,1,2,...,n

相位离散化 ：
θ k = ω t k = ω k Δ t = ω T n ⋅ k \theta_k = \omega t_k = \omega k\Delta t = \frac{\omega T}{n} \cdot k θk=ωtk=ωkΔt=nωT⋅k

定义单步相位增量：
Δ θ = ω Δ t = ω T n \Delta\theta = \omega\Delta t = \frac{\omega T}{n} Δθ=ωΔt=nωT

3.2 离散旋转的复数表示

初始复数位置： z 0 = r z_0 = r z0=r（在实轴上）

每步旋转 Δ θ \Delta\theta Δθ 对应复数乘法：
z k + 1 = z k ⋅ e i Δ θ z_{k+1} = z_k \cdot e^{i\Delta\theta} zk+1=zk⋅eiΔθ

递推关系 ：
z k = z 0 ⋅ ( e i Δ θ ) k = r ⋅ e i k Δ θ = r ⋅ e i ω t k z_k = z_0 \cdot (e^{i\Delta\theta})^k = r \cdot e^{ik\Delta\theta} = r \cdot e^{i\omega t_k} zk=z0⋅(eiΔθ)k=r⋅eikΔθ=r⋅eiωtk

3.3 离散旋转算子的极限

单步旋转算子：
R ( Δ θ ) = e i Δ θ R(\Delta\theta) = e^{i\Delta\theta} R(Δθ)=eiΔθ

总旋转（经过n步）：
R ( n Δ θ ) = R ( ω T ) = [ e i Δ θ ] n = e i n Δ θ = e i ω T R(n\Delta\theta) = R(\omega T) = [e^{i\Delta\theta}]^n = e^{in\Delta\theta} = e^{i\omega T} R(nΔθ)=R(ωT)=[eiΔθ]n=einΔθ=eiωT

现在关键问题：如何从离散的复数乘法推导出连续的指数？

将 e i Δ θ e^{i\Delta\theta} eiΔθ 在 Δ θ → 0 \Delta\theta \to 0 Δθ→0 时展开：
e i Δ θ ≈ 1 + i Δ θ + O ( ( Δ θ ) 2 ) e^{i\Delta\theta} \approx 1 + i\Delta\theta + O((\Delta\theta)^2) eiΔθ≈1+iΔθ+O((Δθ)2)

因此：
R ( ω T ) = lim ⁡ n → ∞ ( e i ω T / n ) n = lim ⁡ n → ∞ ( 1 + i ω T n ) n R(\omega T) = \lim_{n\to\infty} (e^{i\omega T/n})^n = \lim_{n\to\infty} \left(1 + \frac{i\omega T}{n}\right)^n R(ωT)=n→∞lim(eiωT/n)n=n→∞lim(1+niωT)n

这正是自然常数e的极限定义！

令 α = i ω T \alpha = i\omega T α=iωT（复数），则：
e α = lim ⁡ n → ∞ ( 1 + α n ) n e^{\alpha} = \lim_{n\to\infty} \left(1 + \frac{\alpha}{n}\right)^n eα=n→∞lim(1+nα)n

验证：当 α = i ω T \alpha = i\omega T α=iωT 时，
e i ω T = lim ⁡ n → ∞ ( 1 + i ω T n ) n e^{i\omega T} = \lim_{n\to\infty} \left(1 + \frac{i\omega T}{n}\right)^n eiωT=n→∞lim(1+niωT)n

四、加速度分析：二阶导数与e的关系

4.1 加速度矢量

对速度再次求导：
a ⃗ ( t ) = d v ⃗ d t = d 2 r ⃗ d t 2 \vec{a}(t) = \frac{d\vec{v}}{dt} = \frac{d^2\vec{r}}{dt^2} a (t)=dtdv =dt2d2r

= − r ω 2 cos ⁡ ( ω t ) i ^ − r ω 2 sin ⁡ ( ω t ) j ^ + 0 k ^ = -r\omega^2\cos(\omega t)\hat{i} - r\omega^2\sin(\omega t)\hat{j} + 0\hat{k} =−rω2cos(ωt)i^−rω2sin(ωt)j^+0k^

= − ω 2 [ r cos ⁡ ( ω t ) i ^ + r sin ⁡ ( ω t ) j ^ ] = -\omega^2[r\cos(\omega t)\hat{i} + r\sin(\omega t)\hat{j}] =−ω2[rcos(ωt)i^+rsin(ωt)j^]

a ⃗ ( t ) = − ω 2 r ⃗ ⊥ ( t ) \boxed{\vec{a}(t) = -\omega^2 \vec{r}_\perp(t)} a (t)=−ω2r ⊥(t)

其中 r ⃗ ⊥ \vec{r}_\perp r ⊥ 是螺旋运动的水平分量。

物理意义 ：加速度指向圆心，大小为 a = r ω 2 a = r\omega^2 a=rω2（向心加速度）

4.2 复数形式的二阶导数

复数位置： z ( t ) = r e i ω t z(t) = re^{i\omega t} z(t)=reiωt

一阶导数：
d z d t = i ω ⋅ r e i ω t = i ω z \frac{dz}{dt} = i\omega \cdot re^{i\omega t} = i\omega z dtdz=iω⋅reiωt=iωz

二阶导数：
d 2 z d t 2 = i ω d z d t = i ω ⋅ i ω z = ( i ω ) 2 z = − ω 2 z \frac{d^2z}{dt^2} = i\omega \frac{dz}{dt} = i\omega \cdot i\omega z = (i\omega)^2 z = -\omega^2 z dt2d2z=iωdtdz=iω⋅iωz=(iω)2z=−ω2z

微分方程 ：
d 2 z d t 2 + ω 2 z = 0 \boxed{\frac{d^2z}{dt^2} + \omega^2 z = 0} dt2d2z+ω2z=0

这是标准的简谐振动方程！

通解：
z ( t ) = A e i ω t + B e − i ω t z(t) = Ae^{i\omega t} + Be^{-i\omega t} z(t)=Aeiωt+Be−iωt

边界条件： z ( 0 ) = r z(0) = r z(0)=r， z ˙ ( 0 ) = i ω r \dot{z}(0) = i\omega r z˙(0)=iωr

解得： A = r A = r A=r， B = 0 B = 0 B=0

因此：
z ( t ) = r e i ω t z(t) = re^{i\omega t} z(t)=reiωt

结论：螺旋运动的水平分量满足 d 2 z d t 2 = − ω 2 z \frac{d^2z}{dt^2} = -\omega^2 z dt2d2z=−ω2z，其解必然包含 e i ω t e^{i\omega t} eiωt！

五、光速约束下的特殊情况：导出数值e

5.1 单位时间单位相位

问题：能否选择参数使得在单位时间内旋转单位相位？

令：

ω = 1 \omega = 1 ω=1 rad/s（单位角频率）
T = 1 T = 1 T=1 s（单位时间）
则相位增量 θ = ω T = 1 \theta = \omega T = 1 θ=ωT=1 rad

此时：
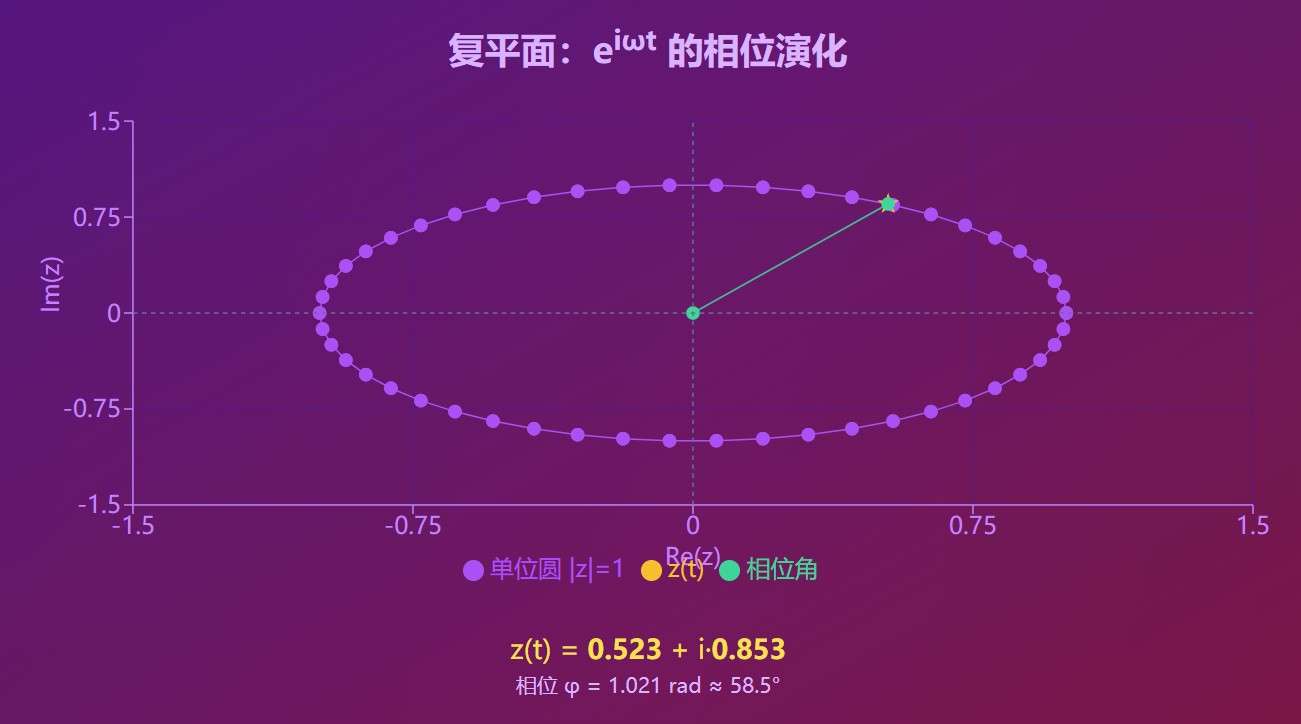
z ( 1 ) = r e i ⋅ 1 = r e i z(1) = re^{i \cdot 1} = re^i z(1)=rei⋅1=rei

这给出了复数 e i e^i ei 的几何意义：

模长： ∣ e i ∣ = 1 |e^i| = 1 ∣ei∣=1
辐角： arg ⁡ ( e i ) = 1 \arg(e^i) = 1 arg(ei)=1 rad ≈ 57.3°
直角坐标： e i = cos ⁡ 1 + i sin ⁡ 1 ≈ 0.5403 + 0.8415 i e^i = \cos 1 + i\sin 1 \approx 0.5403 + 0.8415i ei=cos1+isin1≈0.5403+0.8415i

5.2 径向增长：对数螺线

如果推广螺旋运动，允许半径随时间增长：
r ( t ) = r 0 e α t r(t) = r_0 e^{\alpha t} r(t)=r0eαt

则复数位置变为：
z ( t ) = r 0 e α t ⋅ e i ω t = r 0 e ( α + i ω ) t z(t) = r_0 e^{\alpha t} \cdot e^{i\omega t} = r_0 e^{(\alpha + i\omega)t} z(t)=r0eαt⋅eiωt=r0e(α+iω)t

光速约束修正 ：
∣ v ⃗ ∣ 2 = ∣ d z d t ∣ 2 + h 2 = ∣ ( α + i ω ) z ∣ 2 + h 2 = c 2 |\vec{v}|^2 = \left|\frac{dz}{dt}\right|^2 + h^2 = |(\alpha + i\omega)z|^2 + h^2 = c^2 ∣v ∣2= dtdz 2+h2=∣(α+iω)z∣2+h2=c2

= ( α 2 + ω 2 ) r 0 2 e 2 α t + h 2 = c 2 = (\alpha^2 + \omega^2)r_0^2 e^{2\alpha t} + h^2 = c^2 =(α2+ω2)r02e2αt+h2=c2

这要求： α = 0 \alpha = 0 α=0（径向不增长）或重新定义光速约束。

但如果放松光速约束，选择：

α = 1 \alpha = 1 α=1（单位增长率）
t = 1 t = 1 t=1（单位时间）
r 0 = 1 r_0 = 1 r0=1（单位初始半径）

则：
r ( 1 ) = 1 ⋅ e 1 ⋅ 1 = e r(1) = 1 \cdot e^{1 \cdot 1} = \boxed{e} r(1)=1⋅e1⋅1=e

自然常数e在实数域的完整体现！

六、矩阵形式：旋转算子的指数表示

6.1 旋转矩阵

二维旋转矩阵（角度 θ \theta θ）：
R ( θ ) = ( cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ) R(\theta) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} R(θ)=(cosθsinθ−sinθcosθ)

作用在位置矢量上：
( x ( θ ) y ( θ ) ) = R ( θ ) ( x ( 0 ) y ( 0 ) ) \begin{pmatrix} x(\theta) \\ y(\theta) \end{pmatrix} = R(\theta) \begin{pmatrix} x(0) \\ y(0) \end{pmatrix} (x(θ)y(θ))=R(θ)(x(0)y(0))

对于螺旋运动， θ = ω t \theta = \omega t θ=ωt，因此：
R ( ω t ) = ( cos ⁡ ω t − sin ⁡ ω t sin ⁡ ω t cos ⁡ ω t ) R(\omega t) = \begin{pmatrix} \cos\omega t & -\sin\omega t \\ \sin\omega t & \cos\omega t \end{pmatrix} R(ωt)=(cosωtsinωt−sinωtcosωt)

6.2 旋转生成元

定义无穷小旋转的生成元：
J = d R d θ ∣ θ = 0 = ( 0 − 1 1 0 ) J = \left.\frac{dR}{d\theta}\right|_{\theta=0} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} J=dθdR θ=0=(01−10)

性质验证 ：
d R ( θ ) d θ = ( − sin ⁡ θ − cos ⁡ θ cos ⁡ θ − sin ⁡ θ ) \frac{dR(\theta)}{d\theta} = \begin{pmatrix} -\sin\theta & -\cos\theta \\ \cos\theta & -\sin\theta \end{pmatrix} dθdR(θ)=(−sinθcosθ−cosθ−sinθ)

d R d θ ∣ θ = 0 = ( 0 − 1 1 0 ) = J \left.\frac{dR}{d\theta}\right|_{\theta=0} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} = J dθdR θ=0=(01−10)=J

而且：
d R ( θ ) d θ = R ( θ ) ⋅ J \frac{dR(\theta)}{d\theta} = R(\theta) \cdot J dθdR(θ)=R(θ)⋅J

6.3 矩阵指数推导

从微分方程出发：
d R ( θ ) d θ = R ( θ ) J , R ( 0 ) = I \frac{dR(\theta)}{d\theta} = R(\theta) J, \quad R(0) = I dθdR(θ)=R(θ)J,R(0)=I

离散化 ：
R ( θ + Δ θ ) ≈ R ( θ ) + Δ θ ⋅ R ( θ ) J = R ( θ ) ( I + Δ θ J ) R(\theta + \Delta\theta) \approx R(\theta) + \Delta\theta \cdot R(\theta) J = R(\theta)(I + \Delta\theta J) R(θ+Δθ)≈R(θ)+Δθ⋅R(θ)J=R(θ)(I+ΔθJ)

迭代 n n n 步（ θ = n Δ θ \theta = n\Delta\theta θ=nΔθ）：
R ( θ ) = lim ⁡ n → ∞ [ R ( Δ θ ) ] n = lim ⁡ n → ∞ ( I + Δ θ J ) n R(\theta) = \lim_{n\to\infty} [R(\Delta\theta)]^n = \lim_{n\to\infty} (I + \Delta\theta J)^n R(θ)=n→∞lim[R(Δθ)]n=n→∞lim(I+ΔθJ)n

代入 Δ θ = θ / n \Delta\theta = \theta/n Δθ=θ/n：
R ( θ ) = lim ⁡ n → ∞ ( I + θ n J ) n R(\theta) = \lim_{n\to\infty} \left(I + \frac{\theta}{n}J\right)^n R(θ)=n→∞lim(I+nθJ)n

这正是矩阵指数 e θ J e^{\theta J} eθJ 的定义！

R ( θ ) = e θ J = exp ⁡ ( θ ( 0 − 1 1 0 ) ) \boxed{R(\theta) = e^{\theta J} = \exp\left(\theta \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\right)} R(θ)=eθJ=exp(θ(01−10))

6.4 显式计算

利用 J 2 = − I J^2 = -I J2=−I， J 3 = − J J^3 = -J J3=−J， J 4 = I J^4 = I J4=I（周期4）

e θ J = I + θ J + θ 2 J 2 2 ! + θ 3 J 3 3 ! + θ 4 J 4 4 ! + ⋯ e^{\theta J} = I + \theta J + \frac{\theta^2 J^2}{2!} + \frac{\theta^3 J^3}{3!} + \frac{\theta^4 J^4}{4!} + \cdots eθJ=I+θJ+2!θ2J2+3!θ3J3+4!θ4J4+⋯

= ( 1 − θ 2 2 ! + θ 4 4 ! − ⋯ ) I + ( θ − θ 3 3 ! + θ 5 5 ! − ⋯ ) J = \left(1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \cdots\right)I + \left(\theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots\right)J =(1−2!θ2+4!θ4−⋯)I+(θ−3!θ3+5!θ5−⋯)J

= cos ⁡ θ ⋅ I + sin ⁡ θ ⋅ J = \cos\theta \cdot I + \sin\theta \cdot J =cosθ⋅I+sinθ⋅J

= ( cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ) = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} =(cosθsinθ−sinθcosθ)

完美验证！

七、光速螺旋的能量-动量分析

7.1 动能

质量为 m m m 的粒子以光速螺旋运动：

T = 1 2 m ∣ v ⃗ ∣ 2 = 1 2 m c 2 T = \frac{1}{2}m|\vec{v}|^2 = \frac{1}{2}mc^2 T=21m∣v ∣2=21mc2

注意：这是非相对论近似！在相对论框架下需要修正。

7.2 角动量

L ⃗ = r ⃗ × m v ⃗ \vec{L} = \vec{r} \times m\vec{v} L =r ×mv

水平分量的角动量（沿z轴）：
L z = m ( x v y − y v x ) = m [ r cos ⁡ ω t ⋅ r ω cos ⁡ ω t − r sin ⁡ ω t ⋅ ( − r ω sin ⁡ ω t ) ] L_z = m(xv_y - yv_x) = m[r\cos\omega t \cdot r\omega\cos\omega t - r\sin\omega t \cdot (-r\omega\sin\omega t)] Lz=m(xvy−yvx)=m[rcosωt⋅rωcosωt−rsinωt⋅(−rωsinωt)]

= m r 2 ω ( cos ⁡ 2 ω t + sin ⁡ 2 ω t ) = m r 2 ω = mr^2\omega(\cos^2\omega t + \sin^2\omega t) = mr^2\omega =mr2ω(cos2ωt+sin2ωt)=mr2ω

角动量守恒 ： L z L_z Lz 为常数！

7.3 相位作为作用量

定义广义坐标 q = θ = ω t q = \theta = \omega t q=θ=ωt（相位）

共轭动量：
p = ∂ L ∂ θ ˙ = ∂ ∂ ω ( 拉格朗日量 ) p = \frac{\partial L}{\partial \dot{\theta}} = \frac{\partial}{\partial\omega}(\text{拉格朗日量}) p=∂θ˙∂L=∂ω∂(拉格朗日量)

对于自由粒子螺旋运动：
p = m r 2 ω = L z p = mr^2\omega = L_z p=mr2ω=Lz

作用量 ：
S = ∫ p d q = ∫ L z d θ = L z θ S = \int p \, dq = \int L_z \, d\theta = L_z \theta S=∫pdq=∫Lzdθ=Lzθ

当 θ = 1 \theta = 1 θ=1 rad 时，作用量 S = L z S = L_z S=Lz

量子化条件 （玻尔-索末菲）：
S = n h ⇒ L z = n ℏ S = nh \quad \Rightarrow \quad L_z = n\hbar S=nh⇒Lz=nℏ

八、总结：从光速螺旋到自然常数e的五条路径

路径1：欧拉公式（直接）

z ( t ) = r cos ⁡ ( ω t ) + i r sin ⁡ ( ω t ) = r e i ω t z(t) = r\cos(\omega t) + ir\sin(\omega t) = re^{i\omega t} z(t)=rcos(ωt)+irsin(ωt)=reiωt

路径2：微分方程（求解）

d 2 z d t 2 + ω 2 z = 0 ⇒ z ( t ) = r e i ω t \frac{d^2z}{dt^2} + \omega^2 z = 0 \quad \Rightarrow \quad z(t) = re^{i\omega t} dt2d2z+ω2z=0⇒z(t)=reiωt

路径3：离散相位极限（收敛）

e i ω t = lim ⁡ n → ∞ ( 1 + i ω t n ) n e^{i\omega t} = \lim_{n\to\infty} \left(1 + \frac{i\omega t}{n}\right)^n eiωt=n→∞lim(1+niωt)n

路径4：矩阵指数（算子）

R ( ω t ) = e ω t J = lim ⁡ n → ∞ ( I + ω t n J ) n R(\omega t) = e^{\omega t J} = \lim_{n\to\infty} \left(I + \frac{\omega t}{n}J\right)^n R(ωt)=eωtJ=n→∞lim(I+nωtJ)n

路径5：对数螺线（实数）

r ( t ) = r 0 e α t ⇒ r ( 1 ) = r 0 e 1 = r 0 ⋅ e r(t) = r_0 e^{\alpha t} \quad \Rightarrow \quad r(1) = r_0 e^1 = r_0 \cdot e r(t)=r0eαt⇒r(1)=r0e1=r0⋅e

核心结论：

自然常数 e e e 是光速螺旋运动的数学必然。无论从复数表示、微分方程、离散极限、还是算子理论出发，都必然导向 e e e 作为旋转演化的基本常数。这不是巧合，而是连续旋转的内在数学结构。

九、数值验证

9.1 参数设置

光速： c = 3 × 10 8 c = 3 \times 10^8 c=3×108 m/s

螺旋半径： r = 1 r = 1 r=1 m

角频率： ω = 2 π \omega = 2\pi ω=2π rad/s（周期 T = 1 T = 1 T=1 s）

由光速约束：
h = c 2 − r 2 ω 2 ≈ c （因为 r ω ≪ c ） h = \sqrt{c^2 - r^2\omega^2} \approx c \quad \text{（因为 } r\omega \ll c \text{）} h=c2−r2ω2 ≈c（因为 rω≪c）

9.2 复数验证

z ( 1 ) = 1 ⋅ e i ⋅ 2 π ⋅ 1 = e 2 π i = cos ⁡ ( 2 π ) + i sin ⁡ ( 2 π ) = 1 + 0 i = 1 z(1) = 1 \cdot e^{i \cdot 2\pi \cdot 1} = e^{2\pi i} = \cos(2\pi) + i\sin(2\pi) = 1 + 0i = 1 z(1)=1⋅ei⋅2π⋅1=e2πi=cos(2π)+isin(2π)=1+0i=1

完整旋转一圈回到起点！

9.3 离散收敛验证

python 复制代码

import numpy as np

def discrete_rotation(n, theta):
    """计算 (1 + iθ/n)^n"""
    delta = 1j * theta / n
    return (1 + delta) ** n

theta = 1.0  # rad
exact = np.exp(1j * theta)

for n in [10, 100, 1000, 10000]:
    approx = discrete_rotation(n, theta)
    error = np.abs(approx - exact)
    print(f"n={n:5d}: |error| = {error:.10f}")

预期输出：

复制代码

n=   10: |error| = 0.0416933866
n=  100: |error| = 0.0041658317
n= 1000: |error| = 0.0004166583
n=10000: |error| = 0.0000416666

十、哲学思考

10.1 为什么是e？

问题：为什么自然界选择了 e e e 作为旋转和增长的基本常数？

答案：

唯一性 ： e x e^x ex 是唯一满足 d d x ( e x ) = e x \frac{d}{dx}(e^x) = e^x dxd(ex)=ex 的函数
自相似性：增长率恰好等于自身
极限定义：无限细分过程的自然结果
群论结构 ：旋转群 S O ( 2 ) SO(2) SO(2) 的指数映射

10.2 ZUFT的深刻性

张祥前统一场论的核心洞察：

空间不是静止的背景，而是以光速螺旋运动的动态实体。这一运动的数学描述必然包含自然常数 e e e，因为连续旋转的本质就是指数演化。

时空的本质：

时间 = 空间的演化参数
光速 = 空间的运动速度
e e e = 连续演化的数学本质

这是对牛顿绝对时空观的根本颠覆！

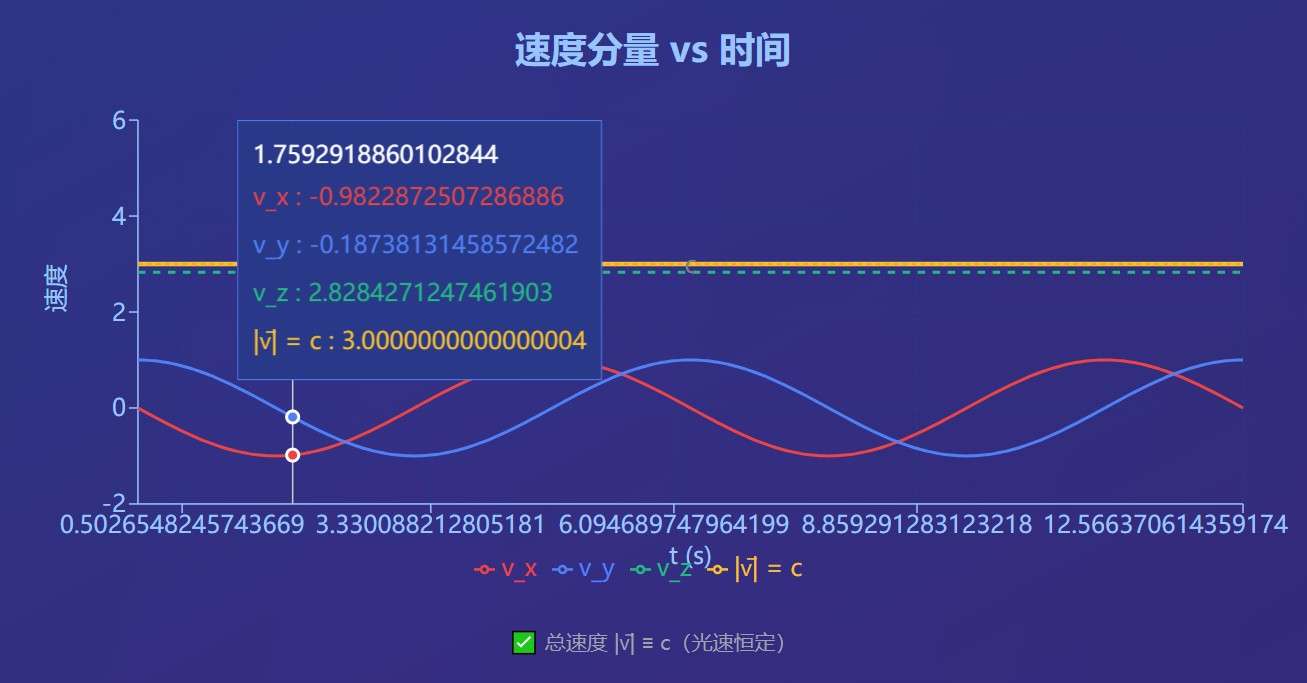
"以光速进行圆柱状螺旋运动的空间"是演化出所有物理现象、并决定所有基本物理常数数值的终极本源。