硅基计划4.0 算法动态规划入门

文章目录

一、斐波那契数大类
- [1. 第N个泰波那契数](#1. 第N个泰波那契数)
- [2. 三步之和](#2. 三步之和)
- [3. 使用最小花费爬楼梯](#3. 使用最小花费爬楼梯)
- [4. 解码方法](#4. 解码方法)
二、路径大类
- [1. 不同路径](#1. 不同路径)
- [2. 不同路径II](#2. 不同路径II)
- [3. 珠宝的最高价值](#3. 珠宝的最高价值)
- [4. 下降路径最小和](#4. 下降路径最小和)
- [5. 最小路径和](#5. 最小路径和)
- [6. 地下城游戏](#6. 地下城游戏)

一、斐波那契数大类

1. 第N个泰波那契数

题目链接

我们先来解析这道题，题目让我们求第N个泰波那契数，其实就是让我们求Tn=Tn-1 + Tn-2 + Tn-3，那这不就是我们的斐波那契数模型吗

接下来我们讲讲这一题的动态规划思想，总结为五个步骤状态表示，状态转移方程，初始化，填表顺序，返回值，我们一个个来看

首先就是状态表示，我们到时候要创建一个dp表，对于dp表的每一个元素我们都要去分析

根据题目，我们要求的是第N个数，那我们是不是要去N-1 N-2 N-3三个位置进行寻找，那我们是不是可以把这三种状态用一个数组存起来，也就是我们俗话说的dp表

到时候我们需要都时候直接去取就好了

因此我们的状态表示dp[i]表示第i个泰波那契数

好，我们接下来取推导状态转移方程，我们是不是需要的是前三个数字啊

因此我们的状态转移方程就是dp[i] = dp[i-1]+dp[i-2]+dp[i-3]

接下来我们再看看初始化的问题，注意我们填表是要获取前三个位置元素，但是如果是dp[0],dp[1],dp[2]这三个位置是会越界的，并且dp[0]也没有实际意义

那我们为什么还要开辟这个空间呢，这是为了多一个位置尽可能使得初始化没有那么麻烦，后面我会讲到

因此我们初始化为dp[0] = 0,dp[1] = dp[2] = 1

好，我们再看我们的填表顺序，因为我们每一次都是需要的是前三个元素

因此我们要从左向右进行填表

我们来确定返回值，因为要的是第N个数

因此直接返回dp[n]

java 复制代码

class Solution {
    public int tribonacci(int n) {
        int [] dp = new int[n+1];
        if(n <= 0){
            return 0;
        }
        if(n == 1 || n == 2){
            return 1;
        }
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 1;
        for(int i = 3;i <= n;i++){
            dp[i] = dp[i-1]+dp[i-2]+dp[i-3];
        }
        return dp[n];
    }
}

我们再想想，是不是我们每次只需要用到前三个数啊，因此我们可以使用常数的空间优化，使用"滚动数组"

java 复制代码

class Solution {
    public int tribonacci(int n) {
        if(n == 0){
            return 0;
        }
        if(n == 1 || n == 2){
            return 1;
        }
        int dp1 = 0;
        int dp2 = 1;
        int dp3 = 1;
        int dp4 = 0;
        for(int i = 3;i <=n;i++){
            dp4 = dp1+dp2+dp3;
            //状态转移
            dp1 = dp2;
            dp2 = dp3;
            dp3 = dp4;
        }
        return dp4;
    }
}

这一题我们还可以使用递归的记忆化搜索，代码如下

java 复制代码

class Solution {
    int [] memory;
    public int tribonacci(int n) {
        memory = new int[n+1];
        return dfs(n);
    }

    private int dfs(int n){
        if(n == 0){
            return 0;
        }
        if(n == 1 || n == 2){
            memory[n] = 1;
            return memory[n];
        }
        if(memory[n] != 0){
            return memory[n];
        }
        memory[n] = dfs(n-1)+dfs(n-2)+dfs(n-3);
        return memory[n];
    }
}

2. 三步之和

题目链接

这一题本质上就是上楼梯问题，我们针对每一个台阶来分析

比如我上到第四个台阶，我可以从1->4，也可以从2->4，也可以从3->4

我不管你之前是从哪一个台阶来的，反正你到我这里无非就这三种方法，因此我们把这三种方式加起来就好

好，我们就可以以每一个台阶作为媒介，来研究状态表示

状态表示：dp[i]表示到达第i个台阶一共有几种方法

好，我们来研究状态转移方程，我们是不是可以从前三楼的任意一个台阶来呀

状态转移方程：dp[i] = dp[i-1]+dp[i-2]+dp[i-3]，注意不能+1，因为我们研究的是种类不是台阶数量

好，我们再来看看初始化问题，老样子我们还是看看是否会有越界问题，因此我们还是初始化

根据我们状态表示

初始化：dp[0] = 0,dp[1] = 1,dp[2] = 2,dp[3] = 4，多留一个位置作为辅助，后续我会讲到为什么这么做

好，我们再来看看填表顺序，因为我们要的是前三个值，因此从左到右填表

填表顺序：从左到右
返回值：dp[n]

java 复制代码

class Solution {
    public int waysToStep(int n) {
        int [] dp = new int[n+1];
        if(n == 1){
            return 1;
        }
        if(n == 2){
            return 2;
        }
        if(n == 3){
            return 4;
        }
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 4;
        int mod = (int)1e9+7;
        for(int i = 4;i <= n;i++){
            //每次做加法都可能溢出，因此每次加法都要取模
            dp[i] = ((dp[i-1]+dp[i-2])%mod+dp[i-3])%mod;
        }
        return dp[n];
    }
}

优化下空间，使用"滚动数组"

java 复制代码

class Solution {
    public int waysToStep(int n) {
        if(n == 1){
            return 1;
        }
        if(n == 2){
            return 2;
        }
        if(n == 3){
            return 4;
        }
        int dp1 = 1;
        int dp2 = 2;
        int dp3 = 4;
        int dp4 = 0;
        int mod = (int)1e9+7;
        for(int i = 4;i <= n;i++){
            dp4 = ((dp1+dp2)%mod+dp3)%mod;
            dp1 = dp2;
            dp2 = dp3;
            dp3 = dp4;
        }
        return dp4;
    }
}

递归结合记忆化搜索

java 复制代码

class Solution {
    int [] memory;
    int mod = (int)1e9+7;
    public int waysToStep(int n) {
        memory = new int[n+1];
        return dfs(n);
    }

    private int dfs(int n){
        if(n == 1){
            memory[1] = 1;
            return 1;
        }
        if(n == 2){
            memory[2] = 2;
            return 2;
        }
        if(n == 3){
            memory[3] = 4;
            return 4;
        }
        if(memory[n] != 0){
            return memory[n];
        }
        memory[n] = (((dfs(n-1)+dfs(n-2))%mod+dfs(n-3)))%mod;
        return memory[n];
    }
}

3. 使用最小花费爬楼梯

题目链接

这一道题意思就是我们可以从0号1号开始爬楼梯，注意我们到达楼顶的方式是要数组最后一个下标越界才算到楼顶，每一次我们可以向上爬1~2个台阶

好，我们来定义我们的状态表示，dp[i]表示到达i位置所需要的最小花费

那么我们来分析状态转移方程，我们想，想要到达i位置，是不是可以

从i-2位置跨越2个台阶过来同时支付cost[i-2]费用
从i-1位置跨越1个台阶过来同时支付cost[i-1]费用

我们是不是要的是最小值啊，因此我们直接取最小值，因此dp[i] = Math.min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1])

好，我们继续来看初始化，我们要保证我们填写i位置状态的时候不能越界，因此我们要初始化dp[0] = dp[1] = 1，这代表到第0位置（原地）和第1个位置（题目说了可以从这里开始）花的钱

我们继续来看填表顺序，我们要的是前面状态的值，因此我们是从左到右填表

同时我们的返回值是dp[n]

java 复制代码

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int length = cost.length;
        int [] dp = new int[length+1];
        //题目中说了可以从0和1号台阶开始，因此默认是0
        for(int i = 2;i <= length;i++){
            dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[length];
    }
}

当然我们还有另外一种思路，我们可以让dp[i]表示从i位置到楼顶的最小花费

那么这样，我们初始化dp[n-1] = cost[n-1]就表示从i-1位置到达楼顶最小花费，同理dp[n-2]表示从i-2位置到达楼顶的最小花费

那我们推导状态转移方程，因为我们是从当前位置去楼顶，那我们是不是要先知道从下一个位置/下两个位置到楼顶最小花费，再加上当前位置的花费就好啦

因此dp[i] = Math.min(dp[i+1cost[i],dp[i+2]+cost[i])

我们每个状态都是依赖于后边的状态的，因此我们要从右往左填表

返回值注意，我们起点有两个，要返回两个起点的最小值

java 复制代码

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int length = cost.length;
        int [] dp = new int[length];
        dp[length-1] = cost[length-1];
        dp[length-2] = cost[length-2];
        for(int i = length-3;i >= 0;i--){
            dp[i] = Math.min(dp[i+1]+cost[i],dp[i+2]+cost[i]);
        }
        //注意题目中说了起点从0或1开始，要返回两者最小值
        return Math.min(dp[0],dp[1]);
    }
}

4. 解码方法

题目链接

题目的意思就是数字映射字母，并且说06这种前缀0的数字是无效的

好，我们来定义状态表示，dp[i]表示以i位置字符为结尾的时候有多少种解码方法

我们想想看，一个字符映射一个/两个数字，因此我们分类讨论

如果我们只针对一个字符。若当前字符是0，不用看了解码失败，说明我们从开头到现在的解码方式都是错的，前面划分有误；若当前字符非0，则解码成功，说明我们前面划分是正确的；
如果我们针对当前字符和前面一个字符（结合）。如果成功解码（即字符范围在10~26），则代表成功，否则直接作废

因此我们的状态转移方程就是dp[i] = dp[i-1]+dp[i-2]，注意只有在解码成功的时候才加上，因此我们还要一起做判断

我们再看初始化问题，dp[0]表示只有一个字符（字符下标从0开始），如果成功就是1，否则就是0。dp[1]表示有两个字符，分情况（一个字符单独，两个字符结合）...

我们因为需要前面的状态，因此我们的填表顺序就是从左往右，返回值就是dp[length-1]

java 复制代码

class Solution {
    public int numDecodings(String s) {
        char [] ss = s.toCharArray();
        int length = ss.length;
        int [] dp = new int[length];
        //第一个字符只要不是0就可以解码成功
        if(ss[0] != '0'){
            dp[0] = 1;
        }
        //如果只有字符串长度只有1
        if(length == 1){
            return dp[0];
        }
        //第一个字符和第二个字符结合必须满足>=10&&<=26
        //首先来判断第一个字符和第二个字符是不是0，如果有一个是0则不满足情况
        if(ss[0]-'0' != 0 && ss[1]-'0' != 0){
            dp[1]++;
        }
        int num = (ss[0]-'0')*10+(ss[1]-'0');
        if(num >= 10 && num <= 26){
            dp[1] += 1;
        }
        for(int i = 2;i < length;i++){
            //如果i位置单独解码成功
            if(ss[i]-'0' != 0){
                dp[i] += dp[i-1];
            }
            //如果i与i-1位置结合一起解码成功
            int nums = ((ss[i-1]-'0')*10)+(ss[i]-'0');
            if(nums >= 10 && nums <= 26){
                dp[i] += dp[i-2];
            }
        }
        return dp[length-1];
    }
}

但是这样初始化判断是不是太麻烦了，我们是不是可以加入一个虚拟节点，也就是"滚动数组"

这样我们初始化就很方便了，但是注意我们加入一个虚拟节点后和原数组下标正好是错开的，因此下表要-1

并且还要保证后续的填表正确，因此我们dp[0] = 1

java 复制代码

class Solution {
    public int numDecodings(String s) {
        char [] ss = s.toCharArray();
        int length = ss.length;
        //注意整个dp表相对于原字符串向后移了一位
        int [] dp = new int[length+1];
        dp[0] = 1;
        if(ss[0] != '0'){
            dp[1] = 1;
        }
        for(int i = 2;i <= length;i++){
            //如果i位置单独解码成功
            if(ss[i-1]-'0' != 0){
                dp[i] += dp[i-1];
            }
            //如果i与i-1位置结合一起解码成功
            int nums = ((ss[i-2]-'0')*10)+(ss[i-1]-'0');
            if(nums >= 10 && nums <= 26){
                dp[i] += dp[i-2];
            }
        }
        return dp[length];
    }
}

二、路径大类

1. 不同路径

题目链接

这道题就是让我们求到达终点有多少种方法

我们的路线有很多，因此我们可以这样定义状态表示

dp[i][j]表示从起点到达[i,j]位置一共有多少种方式

好，我们再来推导状态转移方程，根据最后一个位置也就是[i,j]位置进行问题划分，我们知道，要想到达[i,j]位置，只能从两个方向来，也就是↓和→

我们的状态转移方程就是dp[i][j] = dp[i-1][j]+dp[i][j-1]，为什么不需要+1呢，因为我们求的是方法数不是步数

好，我们再来想想如何初始化，为了方便后续的填表，也为了不用太难地处理边界情况，我们引入一行和一列作为辅助的虚拟边界

引入虚拟边界后，我们要考虑两个问题，一个是边界数值要保证后续填表正确，并且明确和原数组的下标映射方式

我们再来看看填表顺序，因为我们填表需要依赖左边和上边的值，因此需要从上到下，从左到右集训填表。返回值方面，我们直接返回dp[n][n]就好

java 复制代码

class Solution {
    public int uniquePaths(int m, int n) {
        int [][] dp = new int[m+1][n+1];
        dp[0][1] = 1;
        for(int i = 1;i <= m;i++){
            for(int j = 1;j <= n;j++){
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m][n];
    }
}

当然，这一题也可以用递归的解法，融合记忆化搜索

java 复制代码

class Solution {
    int [][] memory;
    public int uniquePaths(int m, int n) {
        //使用记忆化搜索
        memory = new int[m+1][n+1];
        return dfs(m,n);
    }

    private int dfs(int posx,int posy){
        if(memory[posx][posy] != 0){
            //说明这个位置已经被递归过了
            return memory[posx][posy];
        }
        if(posx == 1 && posy == 1){
            //此时位于起点，算一种方法
            memory[1][1] = 1;
            return memory[1][1];
        }
        if(posx == 0 || posy == 0){
            //此时已经越界
            return 0;
        }
        //此时递归之前先存好值，因为从周边来到这里的方式只有一种
        memory[posx][posy] = dfs(posx, posy-1)+dfs(posx-1, posy);
        return memory[posx][posy];
    }
}

2. 不同路径II

题目链接

这一题就是在上一题基础上增加了一个障碍物选项，因此其他还是一样，只不过要特判

如果当前位置是障碍物，则表示无法到达，因此dp[i][j] = 0

java 复制代码

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int height = obstacleGrid.length;
        int wide = obstacleGrid[0].length;
        int [][] dp = new int[height+1][wide+1];
        dp[0][1] = 1;//dp[1][0] = 1也可以
        for(int i = 1;i <= height;i++){
            for(int j = 1;j <= wide;j++){
                if(obstacleGrid[i-1][j-1] == 1){
                    dp[i][j] = 0;
                    continue;
                }
                dp[i][j] = dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[height][wide];
    }
}

3. 珠宝的最高价值

题目链接

这一天道题还是我们典型的路径问题，因此我们这样取定义状态表示
dp[i][j]表示到达[i,j]位置所能获取到的最大价值

题目说了，我们可以从上面或者是左边来，我们只需取两个路径的最大值再加上当前位置价值就好，因此我们的状态转移方程
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])+frame[i][j]

对于初始化，我们还是多加一行一列作为辅助节点，这样，我们就要明确填表正确性和下标映射关系，好，对于第一行和第一列都是指的到达0位置，我们下标默认都从1开始，因此不需要初始化

填表顺序方面，因为我们需要的是左边和上方的值，因此要从上往下，从左到右进行填表，最后返回dp表右下角值

java 复制代码

class Solution {
    public int jewelleryValue(int[][] frame) {
        int height = frame.length;
        int wide = frame[0].length;
        int [][] dp = new int[height+1][wide+1];
        for(int i = 1;i <= height;i++){
            for(int j = 1;j <= wide;j++){
                dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1])+frame[i-1][j-1];
            }
        }
        return dp[height][wide];
    }
}

4. 下降路径最小和

题目链接

依据题意，结合经验，我们定义dp[i][j]表示到达[i,j]位置的最小下降路径和

那我们来推导状态转移方程，我们要知道，到达当前位置，可以从↘️⬇️↙️三个方向来

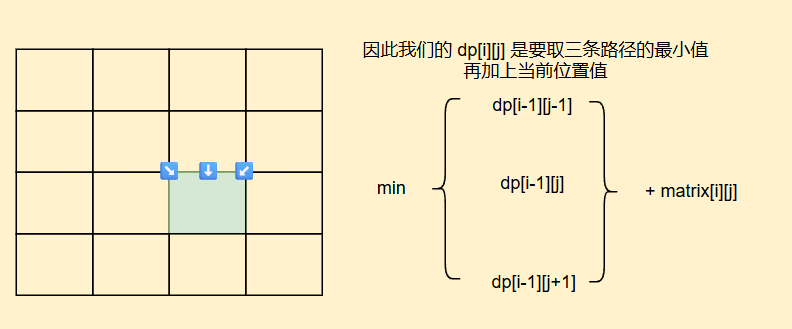
好，我们接下来看初始化，这个初始化特别讲究，我们还是使用辅助行和列进行初始化，当填表在左边界的时候，因为需要左上角，上面，右上角三个地方进行最小值取值，如果我们把边界初始化为0的话，这样最小值比较就会把这个边界0算进去，影响最后判断，因此我们要初始化为+∞，右边界也是一样的道理

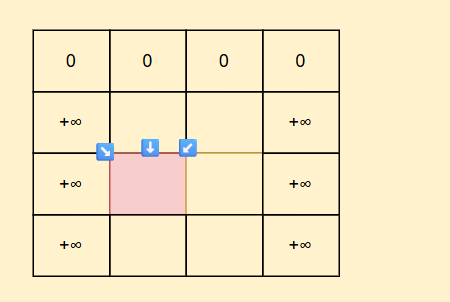
对于填表顺序，我们每次都只会用到上一行值，因此保证从上到下就好

返回值就返回最后一行的最小值，因为我们最后的着陆点可能是最后一行的任意位置

java 复制代码

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int size = matrix.length;
        //注意这里宽度是wide+2，因为要多给一列虚拟列
        int [][] dp = new int[size+1][size+2];
        //初始化dp表
        for(int i = 1;i <= size;i++){
            dp[i][0] = dp[i][size+1] = Integer.MAX_VALUE;
        }
        //进行动态规划计算
        int ret = Integer.MAX_VALUE;
        for(int i = 1;i <= size;i++){
            for(int j = 1;j <= size;j++){
                dp[i][j] = Math.min(Math.min(dp[i-1][j-1],dp[i-1][j]),dp[i-1][j+1])+matrix[i-1][j-1];
                if(i == size){
                    //如果到达最后一行直接判断就好
                    ret = Math.min(ret,dp[i][j]);
                }
            }
        }
        return ret;
    }
}

5. 最小路径和

题目链接

这一题我们根据经验，状态表示为dp[i][j]表示到达[i,j]位置的最小路径和

我们依赖的是上面和左边的值，因此我们状态转移方程就是dp[i,j] = Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j]

这个初始化也是特别讲究，和上一题一样，使用辅助行和辅助列，但是我们也要考虑边界问题

填表顺序，我们依赖上面和左边的值，因此是从上到下，从左到右填表。返回值就是返回dp表右下角值

java 复制代码

class Solution {
    public int minPathSum(int[][] grid) {
        int height = grid.length;
        int wide = grid[0].length;
        int [][] dp = new int[height+1][wide+1];
        //初始化dp表
        for(int i = 0;i <= height;i++){
            Arrays.fill(dp[i],Integer.MAX_VALUE);
        }
        //特殊处理dp表
        dp[0][1] = dp[1][0] = 0;
        for(int i = 1;i <= height;i++){
            for(int j = 1;j <= wide;j++){
                dp[i][j] = Math.min(dp[i-1][j],dp[i][j-1])+grid[i-1][j-1];
            }
        }
        return dp[height][wide];
    }
}

当然这一题也可以使用记忆化搜索

java 复制代码

class Solution {
    int height;
    int wide;
    int [][] memory;
    public int minPathSum(int[][] grid) {
        height = grid.length;
        wide = grid[0].length;
        memory = new int[height][wide];
        return dfs(grid,0,0);
    }

    int [] x = {0,1};
    int [] y = {1,0};

    private int dfs(int [][] grid,int posx,int posy){
        if(memory[posx][posy] != 0){
            return memory[posx][posy];
        }
        if (posx >= height || posy >= wide) {
            //返回最大值，不参与最小路径竞争
            return Integer.MAX_VALUE;
        }
        if(posx == height-1 && posy == wide-1){
            return grid[height-1][wide-1];
        }
        int minPath = Integer.MAX_VALUE;
        for(int i = 0;i < 2;i++){
            int curX = posx+x[i];
            int curY = posy+y[i];
            if(curX >= 0 && curX < height && curY >= 0 && curY < wide){
                minPath = Math.min(minPath,dfs(grid,curX,curY));
            }
        }
        if(minPath == Integer.MAX_VALUE){
            memory[posx][posy] = grid[posx][posy];
        }else{
            memory[posx][posy] = minPath+grid[posx][posy];
        }
        return memory[posx][posy];
    }
}

6. 地下城游戏

题目链接

这一题有点抽象，我们先按照我们传统做法定义一下状态表示
dp[i][j]表示从起点到达[i,j]位置所需要的最低初始状态，但是为什么说这个状态我们无法推导出状态转移方程呢，因为我们在每个牢房可能会有回复生命的道具，一旦恢复，我们的初始生命状态就变化了

也就是说，我们到达[i,j]位置骑士的生命值并不只取决于整体的初始状态，还跟从上面来和从左边来的状态有关

因此我们转变策略，dp[i][j]表示从[i,j]位置到达右下角所需的初始健康点数，这样我们状态只依赖于右边和下边了，这就确保了状态的唯一性

好，我们来推导下状态转移方程，我们的牢房总共就分四类回血，空，掉血，公主

但是请注意，我们的dp[i][j]可能是一个负数，这就代表我们到当前位置不需要任何初始血量，也就代表当前位置是一个回血了很大的牢房

但是我们血量不能用负数表示，因此我们最低初始血量要是一滴血

好，我们接下来看初始化，我们想想，在到达公主牢房后，是不是至少要保证一滴血的血量啊

但是我们到达公主牢房后是不是就到了尽头啊，按照方程我们要去右边和下边的值，那我们已经救到了公主了，因此此时我们就把右边和下边初始化为1，让min比较可以取得1

其他地方边界，我们不能让右边界值和下边界值参与比较，因此我们初始化为+∞就好啦

我们再来看填表顺序，我们都是要右边和下边的值，因此我们要从下往上，从右往左填表。最后返回dp表左上角值就好，别忘了我们状态表示

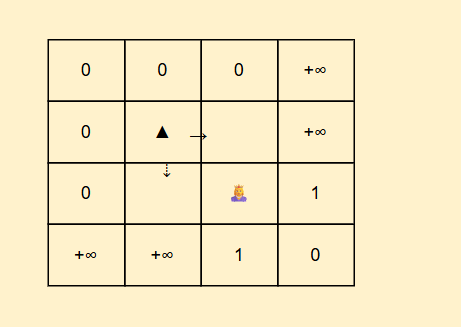
java 复制代码

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        int height = dungeon.length;
        int wide = dungeon[0].length;
        int [][] dp = new int[height+1][wide+1];
        //初始化
        for(int i = 0;i <= height;i++){
            Arrays.fill(dp[i],Integer.MAX_VALUE);
        }
        dp[height][wide-1] = dp[height-1][wide] = 1;
        //开始填表
        for(int i = height-1;i >= 0;i--){
            for(int j = wide-1;j >= 0;j--){
                dp[i][j] = Math.min(dp[i+1][j],dp[i][j+1])-dungeon[i][j];
                dp[i][j] = Math.max(1,dp[i][j]);
            }
        }
        return dp[0][0];
    }
}

感谢你的阅读

END

硅基计划4.0 算法 动态规划入门

文章目录

一、斐波那契数大类

1. 第N个泰波那契数

2. 三步之和

3. 使用最小花费爬楼梯

4. 解码方法

二、路径大类

1. 不同路径

2. 不同路径II

3. 珠宝的最高价值

4. 下降路径最小和

5. 最小路径和

6. 地下城游戏

硅基计划4.0 算法动态规划入门