leetcode 1895. 最大的幻方 中等

一个 k x k 的幻方 指的是一个 k x k 填满整数的方格阵，且每一行、每一列以及两条对角线的和 全部 相等 。幻方中的整数 不需要互不相同 。显然，每个 1 x 1 的方格都是一个幻方。

给你一个 m x n 的整数矩阵 grid ，请你返回矩阵中 最大幻方 的 尺寸 （即边长 k）。

示例 1：

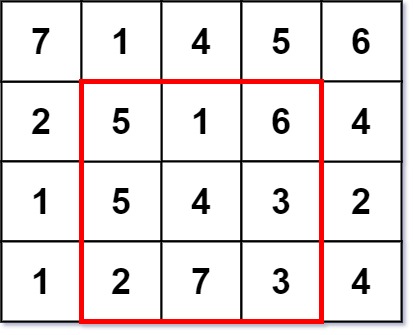
输入：grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
输出：3
解释：最大幻方尺寸为 3 。
每一行，每一列以及两条对角线的和都等于 12 。
- 每一行的和：5+1+6 = 5+4+3 = 2+7+3 = 12
- 每一列的和：5+5+2 = 1+4+7 = 6+3+3 = 12
- 对角线的和：5+4+3 = 6+4+2 = 12

示例 2：

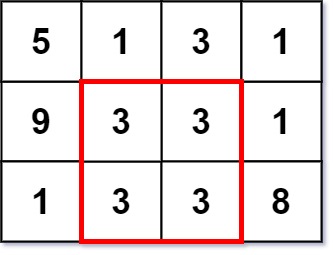
输入：grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
输出：2

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• 1 <= grid[i][j] <= 10^6

分析：先求出水平、垂直、主对角线、反对角线的前缀和，再枚举幻方边长，遍历矩阵的每个点作为左上角点时幻方是否满足条件。

int largestMagicSquare(int** grid, int gridSize, int* gridColSize) {
    int n=gridSize,m=gridColSize[0],ans=1;
    int sum_hor[n+5][m+5],sum_ver[n+5][m+5],sum_lr[n+5][m+5],sum_rl[n+5][m+5];
    for(int i=0;i<=n;++i)
        for(int j=0;j<=m;++j)
            sum_hor[i][j]=sum_ver[i][j]=sum_lr[i][j]=sum_rl[i][j]=0;

    for(int i=0;i<n;++i)
        for(int j=m-1;j>=0;--j)
            sum_hor[i][j]=grid[i][j]+sum_hor[i][j+1];
    for(int j=0;j<m;++j)
        for(int i=n-1;i>=0;--i)
            sum_ver[i][j]=grid[i][j]+sum_ver[i+1][j];
    for(int i=n-1;i>=0;--i)
        for(int j=m-1;j>=0;--j)
            sum_lr[i][j]=grid[i][j]+sum_lr[i+1][j+1];
    for(int i=n-1;i>=0;--i)
        for(int j=0;j<m;++j)
        {
            sum_rl[i][j]=grid[i][j];
            if(j)sum_rl[i][j]+=sum_rl[i+1][j-1];
        }
    
    int maxn=fmin(n,m);
    for(int l=1;l<maxn;++l)
    {
        for(int i=0;i<n-l;++i)
        {
            for(int j=0;j<m-l;++j)
            {
                int temp=sum_lr[i][j]-sum_lr[i+l+1][j+l+1],f1=0;
                if(j-1>=0)
                {
                    if(sum_rl[i][j+l]-sum_rl[i+l+1][j-1]==temp)f1=1;
                }
                else if(sum_rl[i][j+l]==temp)f1=1;

                for(int k=0;k<=l&&f1;++k)
                {
                    if(sum_hor[i+k][j]-sum_hor[i+k][j+l+1]!=temp)f1=0;
                    if(sum_ver[i][j+k]-sum_ver[i+l+1][j+k]!=temp)f1=0;
                }
                if(f1)ans=fmax(ans,l+1);
            }
        }
    }
    
    return ans;
}