MATLAB代码实现了一个带交叉验证的Lasso回归(Lasso Regression)模型,适用于广义线性模型(GLM)框架下的特征选择与正则化回归分析。以下是对该代码的全面分析:
一、研究背景
Lasso回归是一种常用的特征选择与正则化方法 ,通过对回归系数施加L1范数惩罚,使得部分系数趋于零,从而实现变量筛选。该方法特别适用于高维数据 (特征数大于样本数)或存在多重共线性的情形。本代码结合了交叉验证 与广义线性模型,可适应不同分布类型的目标变量。
二、主要功能
- 数据导入:从Excel文件中读取特征矩阵X和目标变量Y。
- 模型配置:支持多种分布类型(正态、泊松、二项等)和链接函数。
- 正则化路径计算:通过设置Lambda序列进行Lasso系数路径分析。
- 交叉验证:使用K折交叉验证选择最优正则化参数λ。
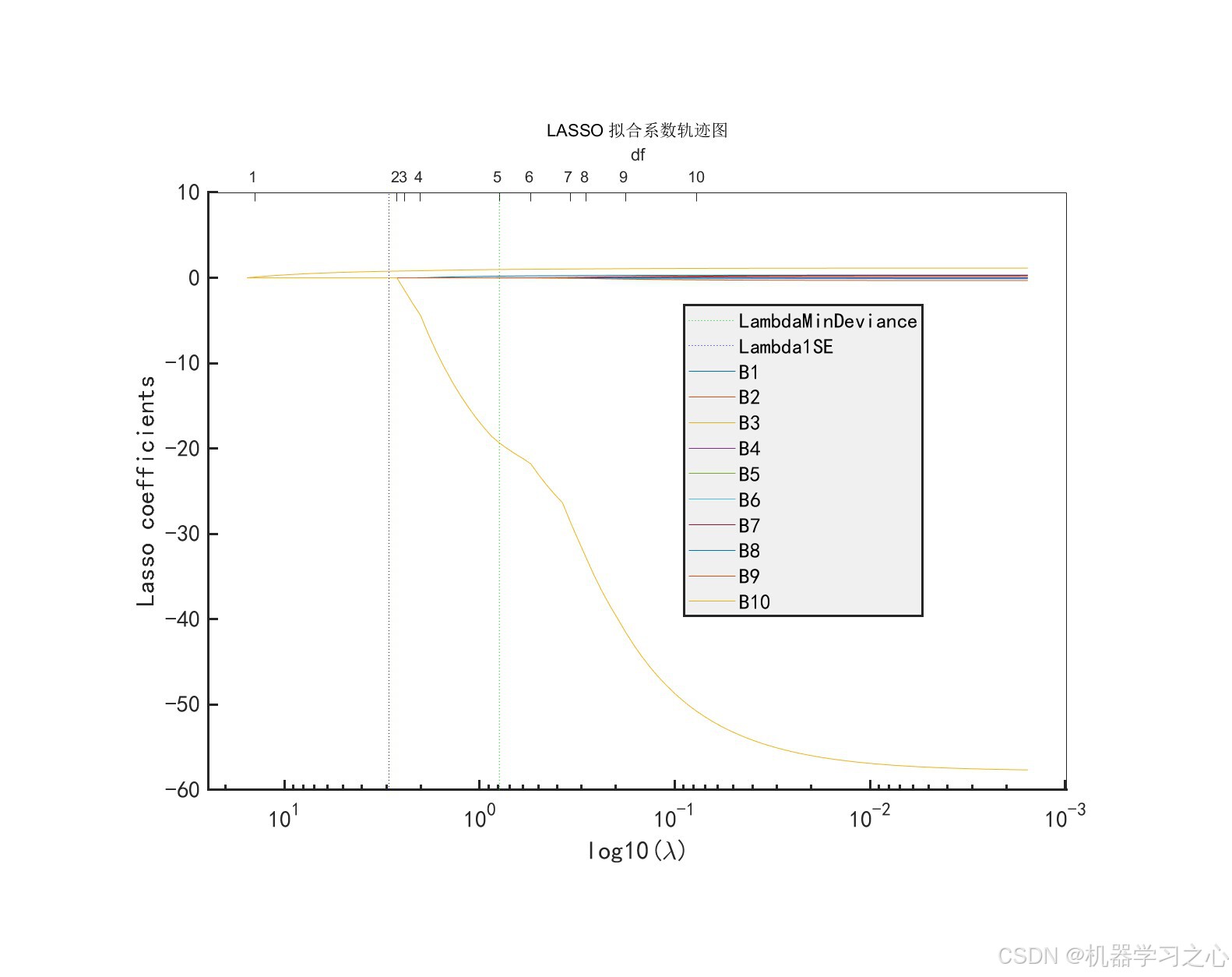
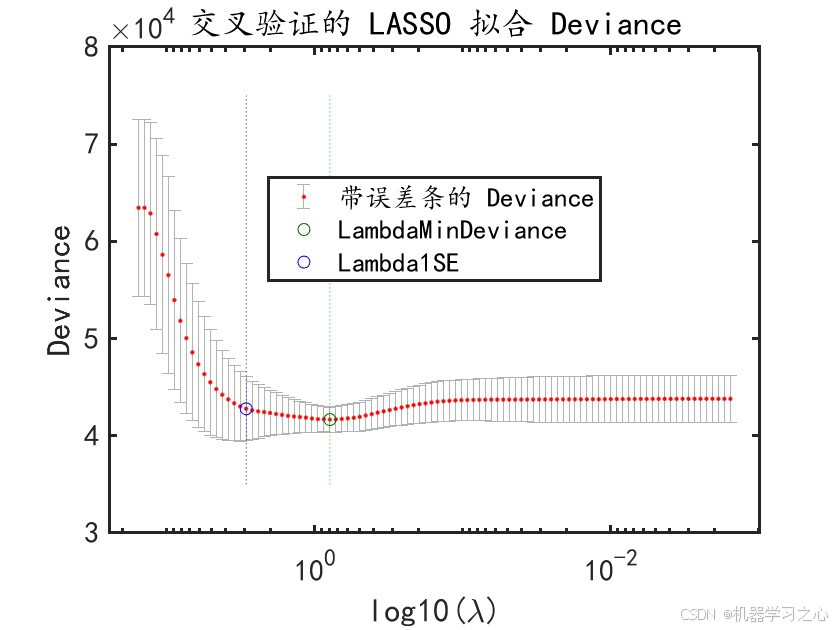
- 结果可视化:绘制系数路径图和交叉验证误差图。
- 特征筛选:输出在最优λ下非零系数对应的特征及其系数值。
三、算法步骤
- 数据准备:读取并分割X和Y。
- 参数验证:检查分布与链接函数的匹配性。
- 模型训练 :调用
lassoglm函数进行Lasso回归。 - 路径分析:绘制系数随λ变化的路径图。
- 交叉验证选择λ :
- 使用最小MSE对应的λ(绿色虚线)
- 使用"1SE原则"对应的λ(蓝色虚线)
- 输出结果:打印非零系数特征及其系数。
四、技术路线
- 核心函数 :
lassoglm(MATLAB内置的Lasso GLM函数) - 可视化 :
lassoPlot - 交叉验证:内置CV选项,支持K折交叉验证
- 正则化路径:通过λ序列计算系数变化路径
五、公式原理
Lasso回归的目标函数为:
minβ{−ℓ(β)+λ∑j=1p∣βj∣} \min_{\beta} \left\{ -\ell(\beta) + \lambda \sum_{j=1}^{p} |\beta_j| \right\} βmin{−ℓ(β)+λj=1∑p∣βj∣}
其中:
- ℓ(β)\ell(\beta)ℓ(β) 是对数似然函数(依赖于分布类型)
- λ\lambdaλ 为正则化参数
- ∑∣βj∣\sum |\beta_j|∑∣βj∣为L1惩罚项,促使系数稀疏化
六、参数设定
| 参数 | 说明 |
|---|---|
distr |
Y的分布类型(normal/binomial/poisson/gamma/inverse gaussian) |
Link |
链接函数,与分布对应 |
Lambda |
正则化系数序列,空则自动生成 |
LambdaRatio |
最小λ与最大λ之比 |
NumLambda |
自动生成的λ数量 |
CV |
K折交叉验证折数 |
seed |
随机种子(保证可重复性) |
Alpha |
弹性网络混合参数(1为Lasso,0为Ridge) |
Standardize |
是否标准化特征 |
七、运行环境
- 软件:MATLAB2020+(需Statistics and Machine Learning Toolbox)
- 数据格式:Excel文件(.xlsx)
- 内存要求:取决于数据规模(100×10示例数据较小)
八、应用场景
- 高维特征选择:如基因表达数据、文本特征、金融指标筛选。
- 模型简化:通过稀疏化降低模型复杂度,提高可解释性。
- 共线性处理:在多重共线性存在时仍可稳定估计。
- 广义线性建模:适用于非正态响应变量(如计数、二分类数据)。
总结
该代码是一个功能完整、参数灵活、输出丰富的Lasso回归实现工具,适用于多种统计建模与特征选择任务,尤其适合需要在广义线性模型框架下进行正则化回归的研究者使用。用户可通过调整λ、分布类型、交叉验证等参数以适应不同数据特点。