leetcode hot100 73.矩阵置零 medium

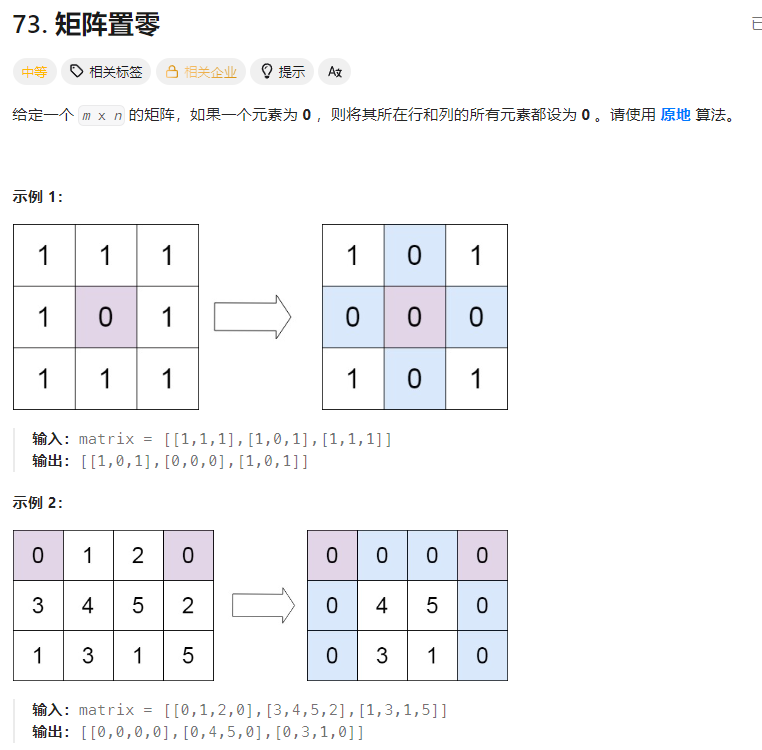
注意是修改原始矩阵的0

暴力解法：

符合题目的要求（原地修改），不过用了额外的空间来存储需要设置为 0 的行和列。

python 复制代码

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        row0 = []
        col0 = []
        m = len(matrix)
        n = len(matrix[0])
        
        for row in range(m):
            for col in range(n):
                if matrix[row][col] == 0:
                    row0.append(row)
                    col0.append(col)

        row0 = set(row0)
        col0 = set(col0)
        for row in row0:
            for j in range(n):
                matrix[row][j] = 0

        for col in col0:
            for i in range(m):
                matrix[i][col] = 0

时间复杂度 ： O(m * n)

第一步：O(m * n)（遍历整个矩阵）

第二步：O(m * n)（修改包含 0 的行）

第三步：O(m * n)（修改包含 0 的列）

所以，总的时间复杂度是 O(m * n)

空间复杂度 ：O(m + n)

使用了两个集合 row0 和 col0 来存储所有为 0 的行和列。

row0 最多包含 m 个行，col0 最多包含 n 个列。因此，空间复杂度是 O(m + n)。

为了优化这个算法，使其空间复杂度从 O(m + n) 降低到 O(1)，我们可以通过原地标记 的方式来避免使用额外的空间（例如 row0 和 col0）。具体的思路如下

优化思路：

使用矩阵的第一行和第一列作为标记：使用第一行来标记哪些列需要置 0。使用第一列来标记哪些行需要置 0
标记到第一行第一列，如果被标记，说明这一行本来也要改为0，所以对第一行第一列的"污染"不影响
再次遍历矩阵，将相应的行和列置 0
最后，检查第一行和第一列，决定是否需要将它们全部置为 0

python 复制代码

class Solution:
    def setZeroes(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        m = len(matrix)
        n = len(matrix[0])
        
        # 标记第一行和第一列是否需要置为0，布尔值
        row0 = False
        for j in range(n):
            if matrix[0][j] == 0:
                row0 =  True

        col0 =  False
        for i in range(m):
            if matrix[i][0] == 0:
                col0 =  True

        # 遍历时从第二行和第二列开始：
        # 标记到第一行第一列，如果被标记，说明这一行本来也要改为0，所以对第一行第一列的"污染"不影响
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][j] == 0:
                    matrix[i][0] = 0  # 标记第 i 行需要置0
                    matrix[0][j] = 0  # 标记第 j 列需要置0    
        
        # 遍历时从第二行和第二列开始：
        # 如果第一行第一列为0，置零
        for i in range(1, m):
            for j in range(1, n):
                if matrix[i][0] == 0 or matrix[0][j] == 0:
                    matrix[i][j] = 0 

        # 最后处理第一行第一列
        if row0:
            for j in range(n):
                matrix[0][j] = 0 
        if col0:
            for i in range(m):
                matrix[i][0] = 0