《机器学习》第三章 - 监督学习

啊阿狸不会拉杆2026-01-21 13:47

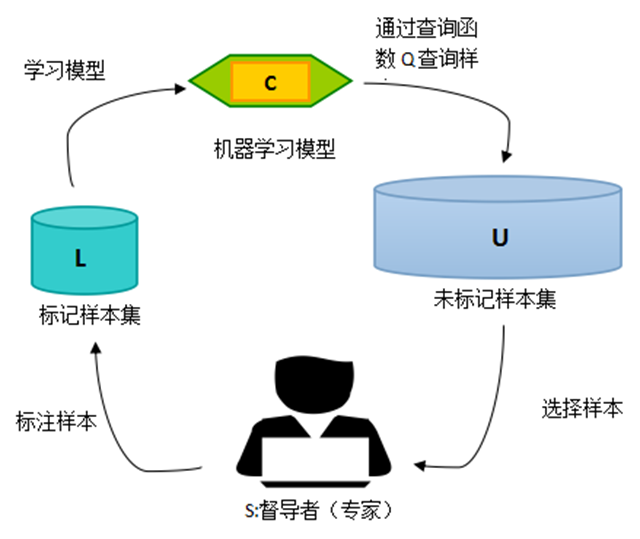
正文

大家好！今天给大家分享《机器学习》第三章监督学习的核心内容，本文会从基础概念到代码实战，把线性模型、决策树、贝叶斯、SVM 这些核心监督学习算法讲透，所有代码均可直接运行，配套可视化对比图，新手也能轻松上手～

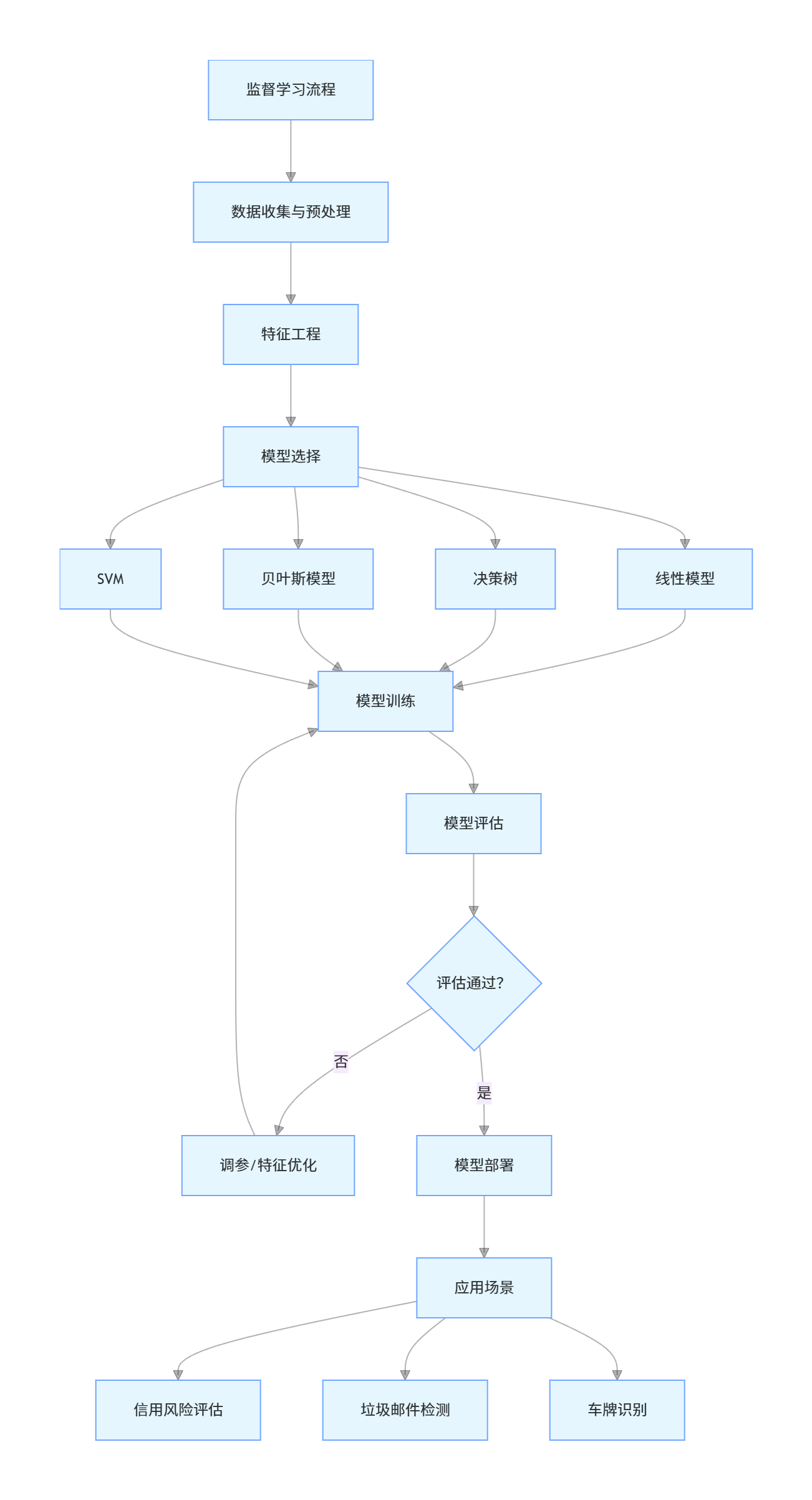
一、思维导图

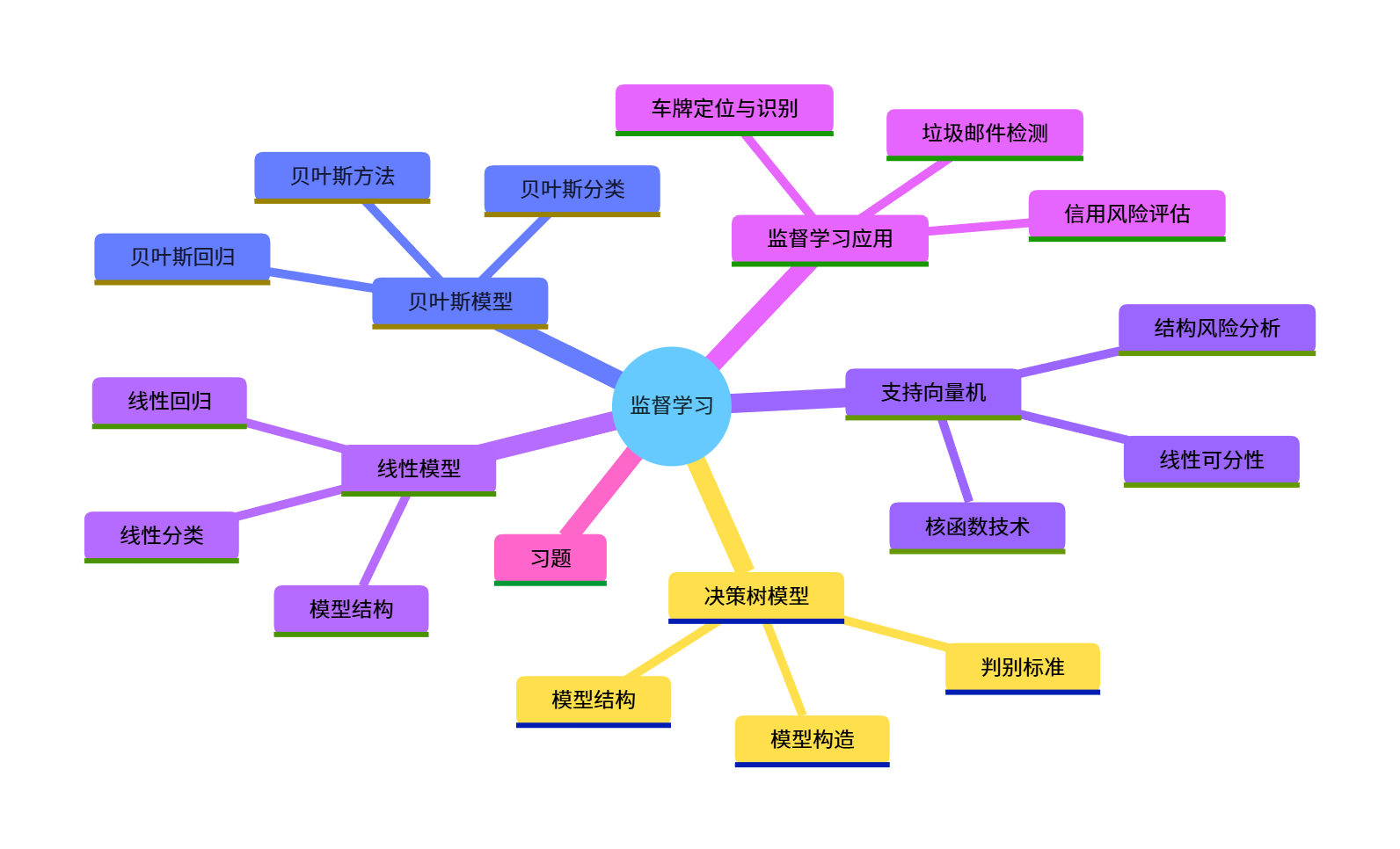
3.1 线性模型

3.1.1 模型结构

线性模型是监督学习中最基础的模型，核心思想是用线性函数拟合输入特征和输出标签的关系，数学表达式为：

3.1.2 线性回归

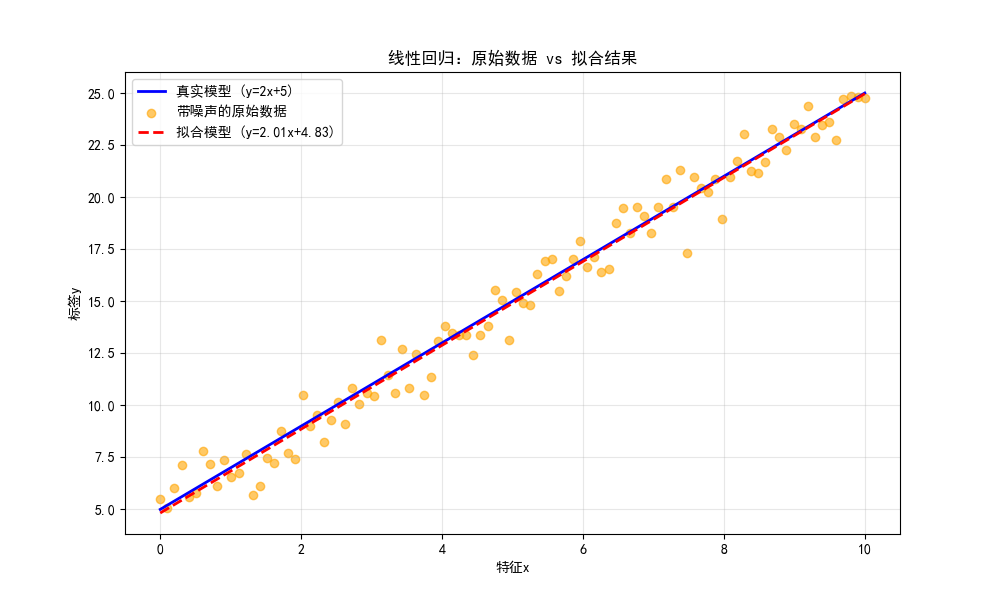
线性回归用于解决回归问题（输出是连续值），核心是通过最小二乘法求解最优权重和偏置。

完整代码 + 可视化对比
复制代码 
import numpy as np
import matplotlib.pyplot as plt
# 设置中文字体，解决matplotlib中文显示问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成模拟数据
np.random.seed(42)  # 固定随机种子，保证结果可复现
x = np.linspace(0, 10, 100)  # 生成0-10的100个均匀数
y_true = 2 * x + 5  # 真实模型：y=2x+5
y_noise = y_true + np.random.normal(0, 1, size=len(x))  # 加入高斯噪声

# 2. 线性回归模型训练
from sklearn.linear_model import LinearRegression
# 转换数据格式（sklearn要求输入是二维数组）
x_reshaped = x.reshape(-1, 1)
model = LinearRegression()
model.fit(x_reshaped, y_noise)  # 拟合数据

# 3. 预测
y_pred = model.predict(x_reshaped)

# 4. 可视化对比（原始数据vs拟合结果）
plt.figure(figsize=(10, 6))
# 绘制原始真实数据
plt.plot(x, y_true, 'b-', label='真实模型 (y=2x+5)', linewidth=2)
# 绘制带噪声的原始数据点
plt.scatter(x, y_noise, c='orange', alpha=0.6, label='带噪声的原始数据')
# 绘制拟合的线性回归模型
plt.plot(x, y_pred, 'r--', label=f'拟合模型 (y={model.coef_[0]:.2f}x+{model.intercept_:.2f})', linewidth=2)

plt.xlabel('特征x')
plt.ylabel('标签y')
plt.title('线性回归：原始数据 vs 拟合结果')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()

# 输出模型参数
print(f"拟合得到的权重w：{model.coef_[0]:.4f}")
print(f"拟合得到的偏置b：{model.intercept_:.4f}")
代码说明
  • np.random.normal：给真实数据加入噪声，模拟真实场景的数据集
  • LinearRegression：sklearn 内置的线性回归模型，自动用最小二乘法求解
  • 可视化部分同时展示了真实模型、带噪声原始数据、拟合模型，直观对比拟合效果

3.1.3 线性分类

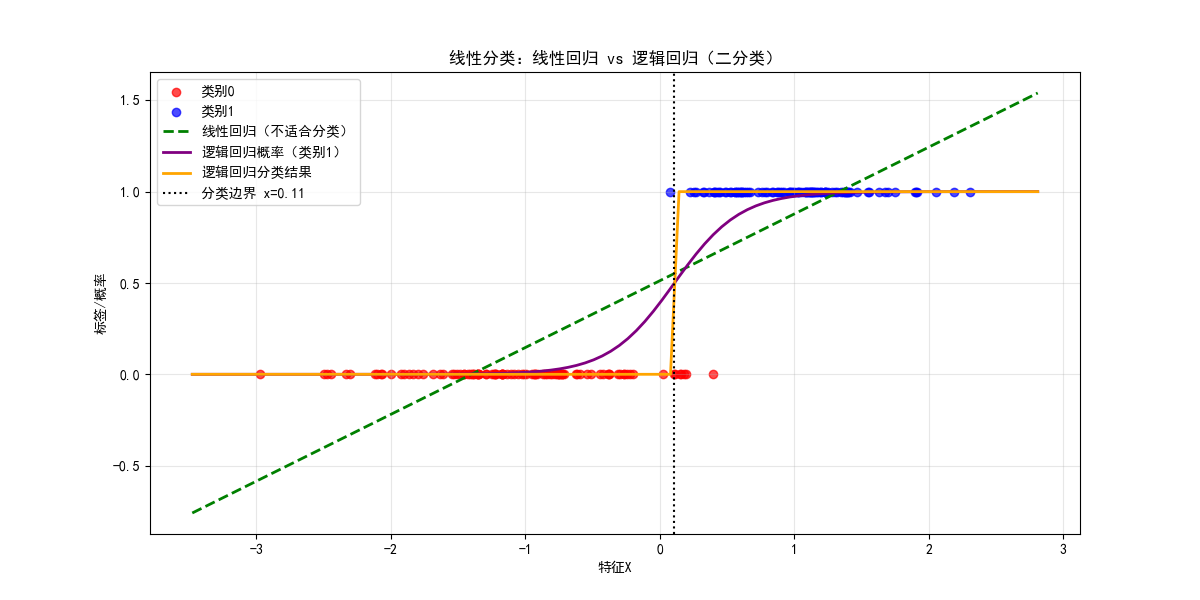
线性分类用于解决分类问题（输出是离散类别），常用的有逻辑回归（二分类）、Softmax 回归（多分类）。这里以逻辑回归为例，对比线性回归和逻辑回归的效果。

完整代码 + 可视化对比
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression, LinearRegression
from sklearn.datasets import make_classification
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成二分类模拟数据
X, y = make_classification(
    n_samples=200, n_features=1, n_informative=1, 
    n_redundant=0, n_classes=2, n_clusters_per_class=1,
    random_state=42
)

# 2. 训练线性回归和逻辑回归模型
# 线性回归（不适合分类）
lr_reg = LinearRegression()
lr_reg.fit(X, y)
y_lr_pred = lr_reg.predict(X)

# 逻辑回归（适合分类）
lr_clf = LogisticRegression()
lr_clf.fit(X, y)
# 生成预测概率和分类结果
x_range = np.linspace(X.min()-0.5, X.max()+0.5, 100).reshape(-1, 1)
y_logit_prob = lr_clf.predict_proba(x_range)[:, 1]
y_logit_pred = lr_clf.predict(x_range)

# 3. 可视化对比（线性回归vs逻辑回归）
plt.figure(figsize=(12, 6))
# 绘制原始数据点
plt.scatter(X[y==0], y[y==0], c='red', label='类别0', alpha=0.7)
plt.scatter(X[y==1], y[y==1], c='blue', label='类别1', alpha=0.7)

# 绘制线性回归结果
plt.plot(x_range, lr_reg.predict(x_range), 'g--', label='线性回归（不适合分类）', linewidth=2)
# 绘制逻辑回归概率曲线和分类边界
plt.plot(x_range, y_logit_prob, 'purple', label='逻辑回归概率（类别1）', linewidth=2)
plt.plot(x_range, y_logit_pred, 'orange', label='逻辑回归分类结果', linewidth=2)
# 绘制分类边界
decision_boundary = -lr_clf.intercept_[0] / lr_clf.coef_[0][0]
plt.axvline(x=decision_boundary, color='black', linestyle=':', label=f'分类边界 x={decision_boundary:.2f}')

plt.xlabel('特征X')
plt.ylabel('标签/概率')
plt.title('线性分类：线性回归 vs 逻辑回归（二分类）')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
代码说明
  • make_classification：生成二分类模拟数据集
  • 逻辑回归通过sigmoid函数将线性输出映射到 0-1 之间（概率），更适合分类
  • 可视化对比了线性回归（连续输出）和逻辑回归（概率 + 分类）的核心差异

3.2 决策树模型

3.2.1 模型结构

决策树是一种树形结构的分类 / 回归模型，由根节点、内部节点、叶节点组成：

  • 根节点：整个数据集的起始点
  • 内部节点：特征判断条件
  • 叶节点：最终的预测结果

3.2.2 判别标准

决策树的核心是选择最优特征划分数据集，常用判别标准：

  • 分类树：信息增益、信息增益比、Gini 系数
  • 回归树：均方误差（MSE）、平均绝对误差（MAE）

3.2.3 模型构造

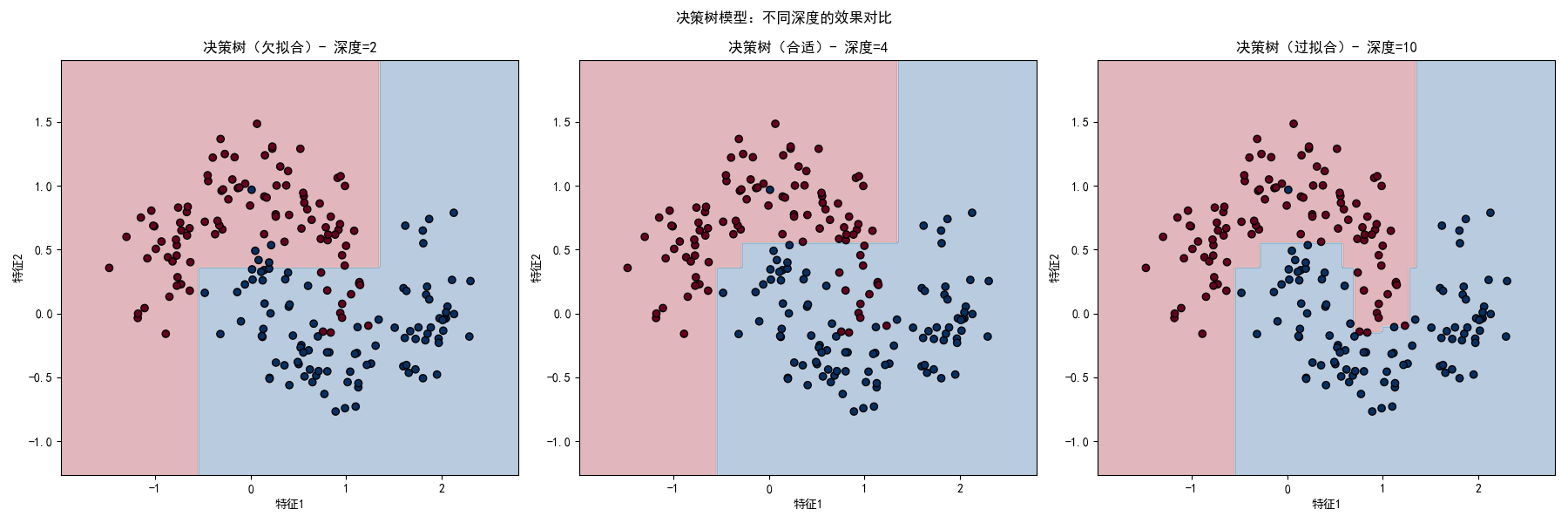
以下代码实现决策树分类，并对比不同深度的决策树效果（过拟合 vs 欠拟合）。

完整代码 + 可视化对比
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.tree import DecisionTreeClassifier, plot_tree
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成非线性可分的模拟数据
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)

# 2. 训练不同深度的决策树
# 欠拟合：深度太小
tree_under = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_under.fit(X, y)

# 过拟合：深度太大
tree_over = DecisionTreeClassifier(max_depth=10, random_state=42)
tree_over.fit(X, y)

# 合适的深度
tree_best = DecisionTreeClassifier(max_depth=4, random_state=42)
tree_best.fit(X, y)

# 3. 生成网格数据用于绘制决策边界
x1_min, x1_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
x2_min, x2_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 200),
                       np.linspace(x2_min, x2_max, 200))
X_grid = np.c_[xx1.ravel(), xx2.ravel()]

# 4. 可视化对比（不同深度决策树的决策边界）
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

# 绘制欠拟合决策树
y_under = tree_under.predict(X_grid).reshape(xx1.shape)
axes[0].contourf(xx1, xx2, y_under, alpha=0.3, cmap='RdBu')
axes[0].scatter(X[:, 0], X[:, 1], c=y, cmap='RdBu', edgecolors='black')
axes[0].set_title('决策树（欠拟合）- 深度=2')
axes[0].set_xlabel('特征1')
axes[0].set_ylabel('特征2')

# 绘制合适深度决策树
y_best = tree_best.predict(X_grid).reshape(xx1.shape)
axes[1].contourf(xx1, xx2, y_best, alpha=0.3, cmap='RdBu')
axes[1].scatter(X[:, 0], X[:, 1], c=y, cmap='RdBu', edgecolors='black')
axes[1].set_title('决策树（合适）- 深度=4')
axes[1].set_xlabel('特征1')
axes[1].set_ylabel('特征2')

# 绘制过拟合决策树
y_over = tree_over.predict(X_grid).reshape(xx1.shape)
axes[2].contourf(xx1, xx2, y_over, alpha=0.3, cmap='RdBu')
axes[2].scatter(X[:, 0], X[:, 1], c=y, cmap='RdBu', edgecolors='black')
axes[2].set_title('决策树（过拟合）- 深度=10')
axes[2].set_xlabel('特征1')
axes[2].set_ylabel('特征2')

plt.suptitle('决策树模型：不同深度的效果对比')
plt.tight_layout()
plt.show()

# 绘制最优决策树的结构
plt.figure(figsize=(15, 8))
plot_tree(tree_best, filled=True, feature_names=['特征1', '特征2'], class_names=['类别0', '类别1'], fontsize=10)
plt.title('决策树结构（深度=4）')
plt.show()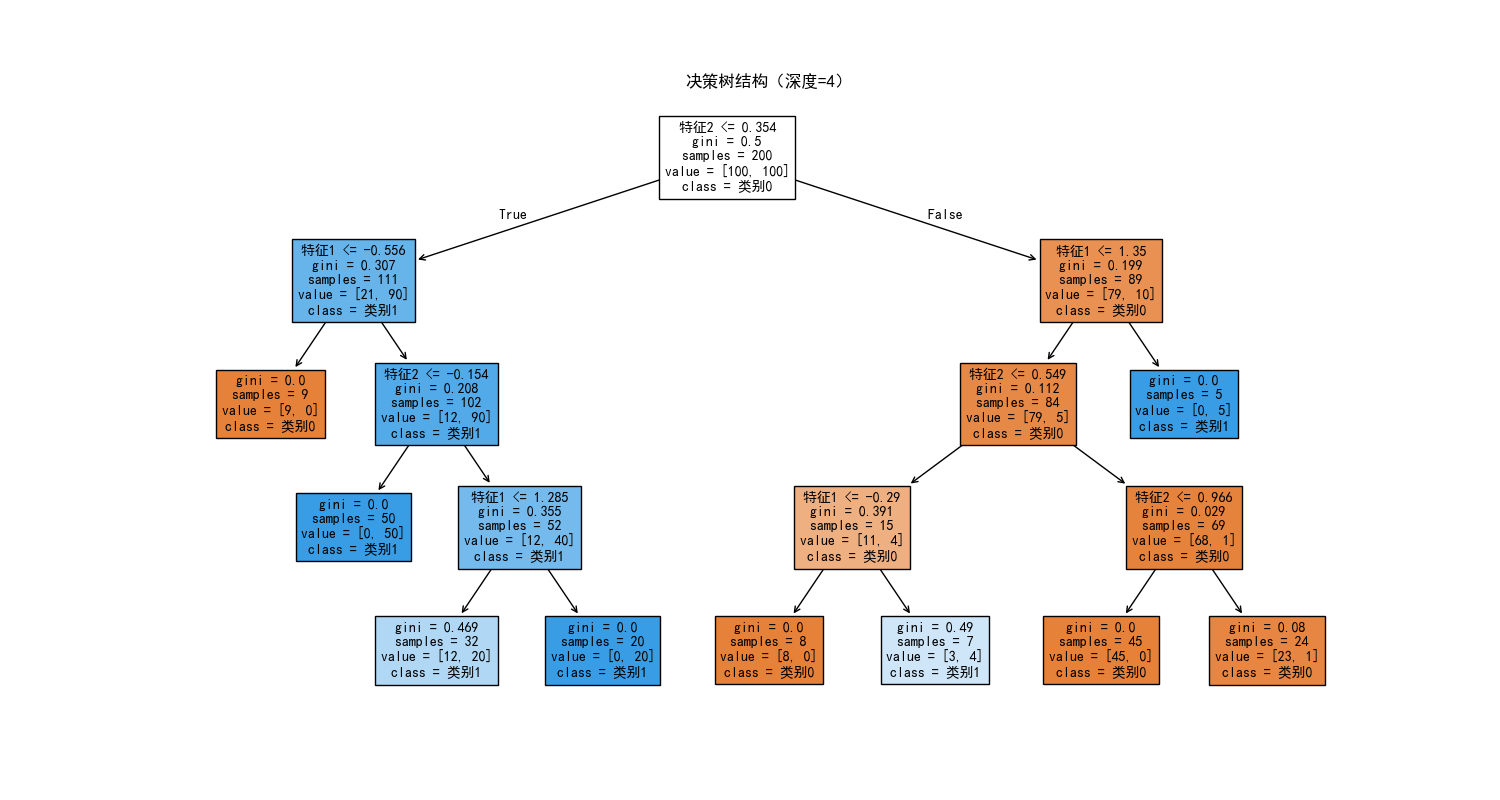
代码说明
  • make_moons：生成非线性可分的月牙形数据，适合测试决策树的非线性拟合能力
  • max_depth：控制决策树深度，是防止过拟合的核心参数
  • 可视化对比了欠拟合（深度 2）、合适（深度 4）、过拟合（深度 10）三种情况的决策边界

3.3 贝叶斯模型

3.3.1 贝叶斯方法

3.3.2 贝叶斯分类

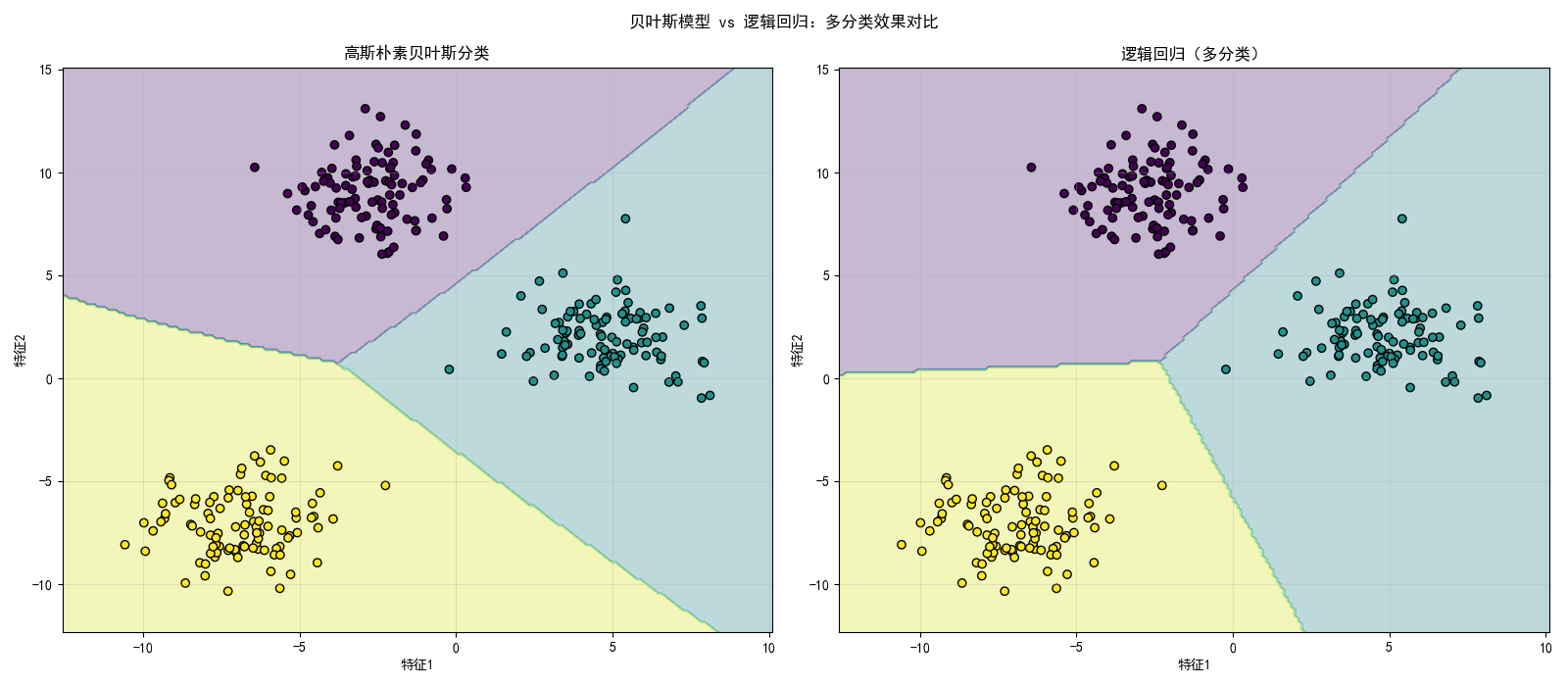
以高斯朴素贝叶斯为例，实现分类任务，并对比贝叶斯和逻辑回归的分类效果。

完整代码 + 可视化对比
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import LogisticRegression
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成多分类模拟数据
X, y = make_blobs(n_samples=300, n_features=2, centers=3, cluster_std=1.5, random_state=42)

# 2. 训练模型
# 高斯朴素贝叶斯
gnb = GaussianNB()
gnb.fit(X, y)

# 逻辑回归（多分类）
lr = LogisticRegression(multi_class='multinomial', random_state=42)
lr.fit(X, y)

# 3. 生成网格数据
x1_min, x1_max = X[:, 0].min() - 2, X[:, 0].max() + 2
x2_min, x2_max = X[:, 1].min() - 2, X[:, 1].max() + 2
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 200),
                       np.linspace(x2_min, x2_max, 200))
X_grid = np.c_[xx1.ravel(), xx2.ravel()]

# 4. 预测
y_gnb = gnb.predict(X_grid).reshape(xx1.shape)
y_lr = lr.predict(X_grid).reshape(xx1.shape)

# 5. 可视化对比（贝叶斯vs逻辑回归）
fig, axes = plt.subplots(1, 2, figsize=(16, 7))

# 贝叶斯分类结果
axes[0].contourf(xx1, xx2, y_gnb, alpha=0.3, cmap='viridis')
axes[0].scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolors='black')
axes[0].set_title('高斯朴素贝叶斯分类')
axes[0].set_xlabel('特征1')
axes[0].set_ylabel('特征2')
axes[0].grid(True, alpha=0.3)

# 逻辑回归分类结果
axes[1].contourf(xx1, xx2, y_lr, alpha=0.3, cmap='viridis')
axes[1].scatter(X[:, 0], X[:, 1], c=y, cmap='viridis', edgecolors='black')
axes[1].set_title('逻辑回归（多分类）')
axes[1].set_xlabel('特征1')
axes[1].set_ylabel('特征2')
axes[1].grid(True, alpha=0.3)

plt.suptitle('贝叶斯模型 vs 逻辑回归：多分类效果对比')
plt.tight_layout()
plt.show()

# 输出分类准确率
print(f"高斯朴素贝叶斯准确率：{gnb.score(X, y):.4f}")
print(f"逻辑回归准确率：{lr.score(X, y):.4f}")

3.3.3 贝叶斯回归

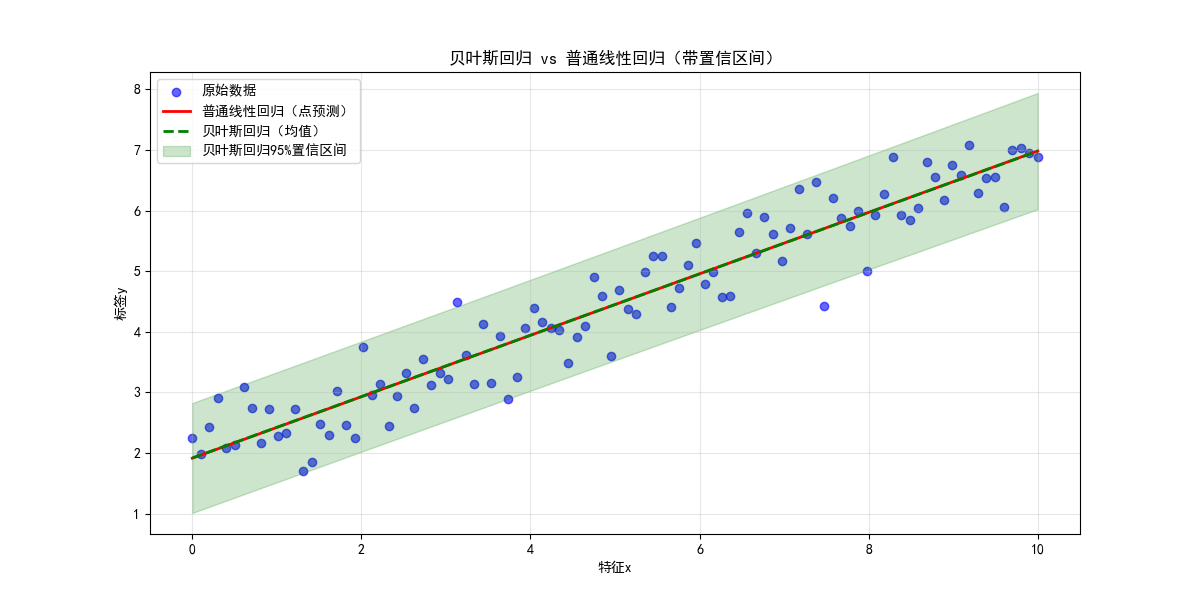
贝叶斯回归结合了贝叶斯推断和线性回归，能给出预测的置信区间（不确定性），对比普通线性回归的点预测。

完整代码 + 可视化对比
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, BayesianRidge
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成模拟数据
np.random.seed(42)
x = np.linspace(0, 10, 100).reshape(-1, 1)
y_true = 0.5 * x + 2 + np.random.normal(0, 0.5, size=x.shape)

# 2. 训练模型
# 普通线性回归
lr = LinearRegression()
lr.fit(x, y_true)
y_lr = lr.predict(x)

# 贝叶斯回归
br = BayesianRidge()
br.fit(x, y_true)
y_br, y_br_std = br.predict(x, return_std=True)  # 返回预测值和标准差

# 3. 可视化对比（普通线性回归vs贝叶斯回归）
plt.figure(figsize=(12, 6))
# 原始数据
plt.scatter(x, y_true, alpha=0.6, label='原始数据', color='blue')
# 普通线性回归
plt.plot(x, y_lr, 'r-', label='普通线性回归（点预测）', linewidth=2)
# 贝叶斯回归（均值+置信区间）
plt.plot(x, y_br, 'g--', label='贝叶斯回归（均值）', linewidth=2)
# 绘制95%置信区间（均值±2*标准差）
plt.fill_between(x.ravel(), y_br.ravel()-2*y_br_std, y_br.ravel()+2*y_br_std, 
                 alpha=0.2, color='green', label='贝叶斯回归95%置信区间')

plt.xlabel('特征x')
plt.ylabel('标签y')
plt.title('贝叶斯回归 vs 普通线性回归（带置信区间）')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
代码说明
  • 贝叶斯回归不仅返回预测值，还返回标准差，可绘制置信区间
  • 置信区间能反映预测的不确定性，这是普通线性回归不具备的优势

3.4 支持向量机

3.4.1 线性可分性

支持向量机（SVM）的核心是寻找最优超平面，最大化分类间隔。对于线性可分数据，SVM 能找到最优分类边界。

3.4.2 核函数技术

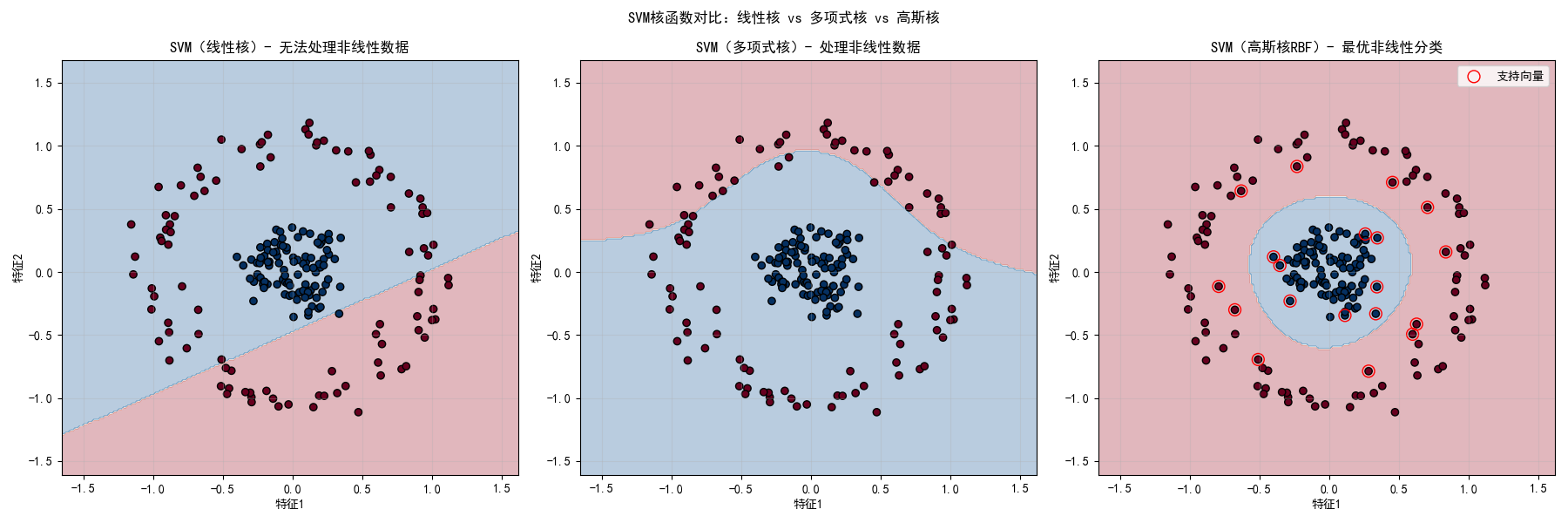
对于非线性可分数据，SVM 通过核函数将数据映射到高维空间，使其线性可分。常用核函数：线性核、多项式核、高斯核（RBF）。

3.4.3 结构风险分析

SVM 通过正则化参数控制模型复杂度，平衡经验风险和结构风险，防止过拟合。

完整代码 + 可视化对比（不同核函数 SVM）
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.svm import SVC
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成非线性可分的环形数据
X, y = make_circles(n_samples=200, noise=0.1, factor=0.2, random_state=42)

# 2. 训练不同核函数的SVM
# 线性核（无法处理非线性数据）
svm_linear = SVC(kernel='linear', C=1.0, random_state=42)
svm_linear.fit(X, y)

# 多项式核
svm_poly = SVC(kernel='poly', degree=3, C=1.0, random_state=42)
svm_poly.fit(X, y)

# 高斯核（RBF）
svm_rbf = SVC(kernel='rbf', gamma='scale', C=1.0, random_state=42)
svm_rbf.fit(X, y)

# 3. 生成网格数据
x1_min, x1_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
x2_min, x2_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 200),
                       np.linspace(x2_min, x2_max, 200))
X_grid = np.c_[xx1.ravel(), xx2.ravel()]

# 4. 预测
y_linear = svm_linear.predict(X_grid).reshape(xx1.shape)
y_poly = svm_poly.predict(X_grid).reshape(xx1.shape)
y_rbf = svm_rbf.predict(X_grid).reshape(xx1.shape)

# 5. 可视化对比（不同核函数SVM）
fig, axes = plt.subplots(1, 3, figsize=(18, 6))

# 线性核SVM
axes[0].contourf(xx1, xx2, y_linear, alpha=0.3, cmap='RdBu')
axes[0].scatter(X[:, 0], X[:, 1], c=y, cmap='RdBu', edgecolors='black')
axes[0].set_title('SVM（线性核）- 无法处理非线性数据')
axes[0].set_xlabel('特征1')
axes[0].set_ylabel('特征2')
axes[0].grid(True, alpha=0.3)

# 多项式核SVM
axes[1].contourf(xx1, xx2, y_poly, alpha=0.3, cmap='RdBu')
axes[1].scatter(X[:, 0], X[:, 1], c=y, cmap='RdBu', edgecolors='black')
axes[1].set_title('SVM（多项式核）- 处理非线性数据')
axes[1].set_xlabel('特征1')
axes[1].set_ylabel('特征2')
axes[1].grid(True, alpha=0.3)

# 高斯核SVM
axes[2].contourf(xx1, xx2, y_rbf, alpha=0.3, cmap='RdBu')
axes[2].scatter(X[:, 0], X[:, 1], c=y, cmap='RdBu', edgecolors='black')
# 绘制支持向量
sv = svm_rbf.support_vectors_
axes[2].scatter(sv[:, 0], sv[:, 1], s=100, facecolors='none', edgecolors='red', label='支持向量')
axes[2].set_title('SVM（高斯核RBF）- 最优非线性分类')
axes[2].set_xlabel('特征1')
axes[2].set_ylabel('特征2')
axes[2].legend()
axes[2].grid(True, alpha=0.3)

plt.suptitle('SVM核函数对比：线性核 vs 多项式核 vs 高斯核')
plt.tight_layout()
plt.show()

# 输出准确率
print(f"线性核SVM准确率：{svm_linear.score(X, y):.4f}")
print(f"多项式核SVM准确率：{svm_poly.score(X, y):.4f}")
print(f"高斯核SVM准确率：{svm_rbf.score(X, y):.4f}")
代码说明
  • make_circles：生成环形非线性可分数据，测试不同核函数的效果
  • 线性核无法处理非线性数据，多项式核和高斯核能有效拟合
  • 高斯核（RBF）是最常用的核函数，适应性最强

3.5 监督学习应用

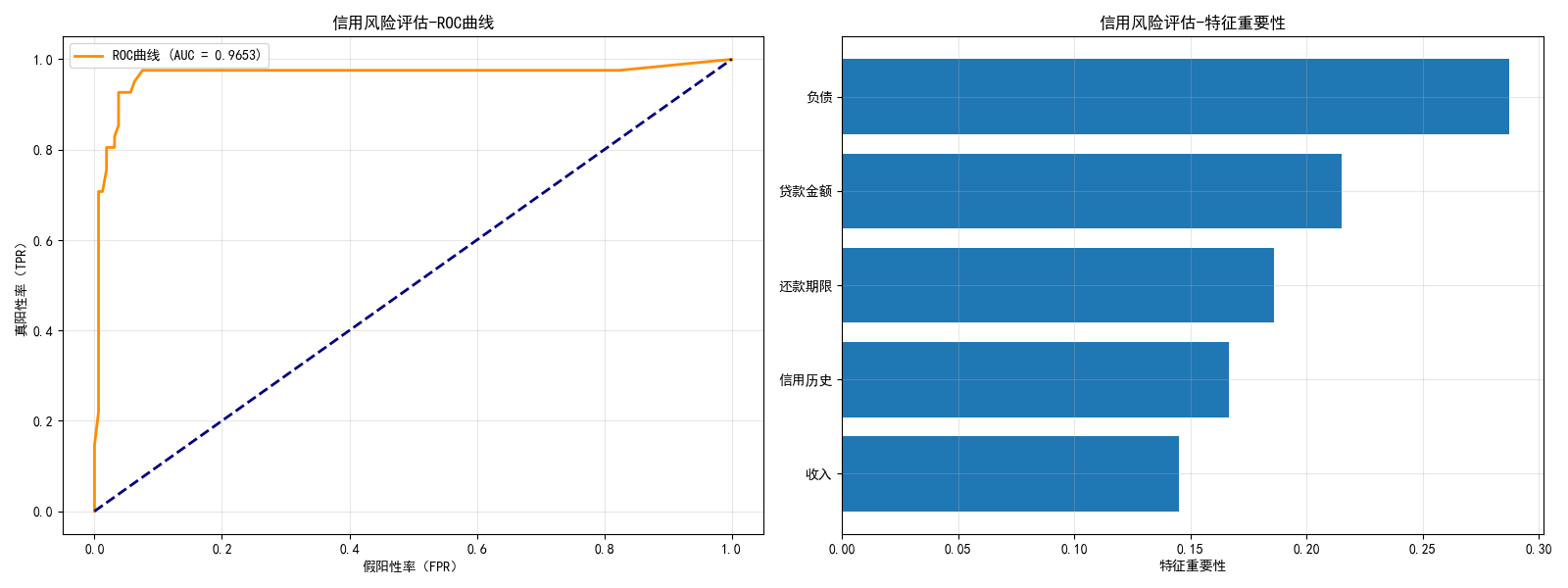
3.5.1 信用风险评估

基于监督学习的分类算法，评估用户的信用风险（违约 / 不违约）。

完整代码
复制代码 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import classification_report, roc_curve, auc
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 生成模拟信用风险数据
# 特征：收入、负债、信用历史、贷款金额、还款期限
X, y = make_classification(
    n_samples=1000, n_features=5, n_informative=4,
    n_redundant=1, n_classes=2, weights=[0.8, 0.2],  # 不平衡数据（80%正常，20%违约）
    random_state=42
)
feature_names = ['收入', '负债', '信用历史', '贷款金额', '还款期限']
df = pd.DataFrame(X, columns=feature_names)
df['违约'] = y

# 2. 数据划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42, stratify=y)

# 3. 训练随机森林模型（集成决策树，效果更好）
rf = RandomForestClassifier(n_estimators=100, random_state=42)
rf.fit(X_train, y_train)

# 4. 预测与评估
y_pred = rf.predict(X_test)
y_pred_prob = rf.predict_proba(X_test)[:, 1]

# 输出分类报告
print("信用风险评估模型报告：")
print(classification_report(y_test, y_pred, target_names=['不违约', '违约']))

# 5. 可视化：ROC曲线 + 特征重要性
fig, axes = plt.subplots(1, 2, figsize=(16, 6))

# ROC曲线
fpr, tpr, _ = roc_curve(y_test, y_pred_prob)
roc_auc = auc(fpr, tpr)
axes[0].plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC曲线 (AUC = {roc_auc:.4f})')
axes[0].plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
axes[0].set_xlabel('假阳性率（FPR）')
axes[0].set_ylabel('真阳性率（TPR）')
axes[0].set_title('信用风险评估-ROC曲线')
axes[0].legend()
axes[0].grid(True, alpha=0.3)

# 特征重要性
importances = rf.feature_importances_
sorted_idx = np.argsort(importances)
axes[1].barh(np.array(feature_names)[sorted_idx], importances[sorted_idx])
axes[1].set_xlabel('特征重要性')
axes[1].set_title('信用风险评估-特征重要性')
axes[1].grid(True, alpha=0.3)

plt.tight_layout()
plt.show()

3.5.2 垃圾邮件检测

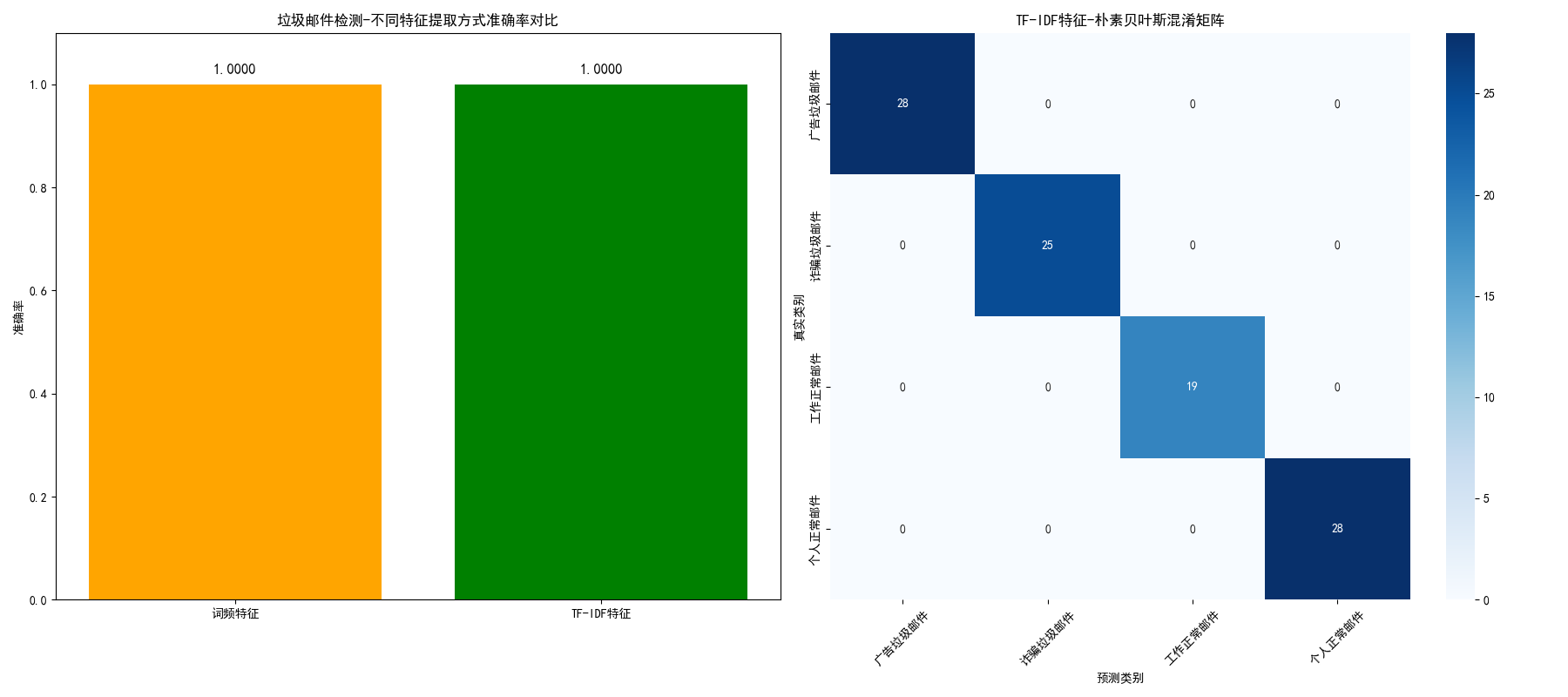
基于贝叶斯分类器（朴素贝叶斯）实现垃圾邮件检测，对比不同特征提取方式的效果。

完整代码
python 复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score, confusion_matrix
import seaborn as sns

# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 构造模拟邮件文本数据（替代20newsgroups）
# 标签说明：0=广告垃圾邮件, 1=诈骗垃圾邮件, 2=工作正常邮件, 3=个人正常邮件
np.random.seed(42)  # 固定随机种子，保证结果可复现

# 定义各类邮件的特征词汇和模板
spam_ad_words = ["促销", "打折", "优惠", "限时", "抢购", "返利", "爆款", "低价", "包邮"]
spam_scam_words = ["中奖", "转账", "验证码", "账户", "安全", "退款", "领奖", "手续费"]
normal_work_words = ["会议", "报告", "项目", "进度", "邮件", "文档", "合作", "方案"]
normal_personal_words = ["周末", "聚餐", "旅行", "家人", "朋友", "生日", "礼物", "假期"]


# 生成模拟文本数据的函数（修正核心：所有return都在函数内部）
def generate_mock_emails(num_samples_per_class=100):
    emails = []
    labels = []

    # 生成广告垃圾邮件
    for _ in range(num_samples_per_class):
        # 随机选3-5个广告词汇生成句子
        words = np.random.choice(spam_ad_words, size=np.random.randint(3, 6), replace=True)
        email = " ".join(words) + " 点击链接立即参与活动！"
        emails.append(email)
        labels.append(0)

    # 生成诈骗垃圾邮件
    for _ in range(num_samples_per_class):
        words = np.random.choice(spam_scam_words, size=np.random.randint(3, 6), replace=True)
        email = " ".join(words) + " 请立即操作避免账户冻结！"
        emails.append(email)
        labels.append(1)

    # 生成工作正常邮件
    for _ in range(num_samples_per_class):
        words = np.random.choice(normal_work_words, size=np.random.randint(3, 6), replace=True)
        email = " ".join(words) + " 请尽快回复确认。"
        emails.append(email)
        labels.append(2)

    # 生成个人正常邮件
    for _ in range(num_samples_per_class):
        words = np.random.choice(normal_personal_words, size=np.random.randint(3, 6), replace=True)
        email = " ".join(words) + " 期待你的回复！"
        emails.append(email)
        labels.append(3)

    # 打乱数据顺序
    combined = list(zip(emails, labels))
    np.random.shuffle(combined)
    emails, labels = zip(*combined)

    return list(emails), list(labels)  # return在函数内部，语法正确


# 生成总数据并划分训练/测试集（修正逻辑：拆分函数职责，避免return混淆）
total_samples_per_class = 125  # 训练100个/类，测试25个/类
all_emails, all_labels = generate_mock_emails(total_samples_per_class)

# 划分训练集和测试集（8:2比例）
train_size = int(len(all_emails) * 0.8)
train_data = all_emails[:train_size]
train_target = all_labels[:train_size]
test_data = all_emails[train_size:]
test_target = all_labels[train_size:]

# 类别名称（用于可视化）
target_names = ["广告垃圾邮件", "诈骗垃圾邮件", "工作正常邮件", "个人正常邮件"]

# 2. 特征提取
# 方式1：词频统计（CountVectorizer）
count_vec = CountVectorizer()  # 中文无需设置stop_words
X_train_count = count_vec.fit_transform(train_data)
X_test_count = count_vec.transform(test_data)

# 方式2：TF-IDF（更适合文本分类）
tfidf_vec = TfidfVectorizer()
X_train_tfidf = tfidf_vec.fit_transform(train_data)
X_test_tfidf = tfidf_vec.transform(test_data)

# 3. 训练朴素贝叶斯模型
# 词频特征模型
nb_count = MultinomialNB()
nb_count.fit(X_train_count, train_target)
y_pred_count = nb_count.predict(X_test_count)

# TF-IDF特征模型
nb_tfidf = MultinomialNB()
nb_tfidf.fit(X_train_tfidf, train_target)
y_pred_tfidf = nb_tfidf.predict(X_test_tfidf)

# 4. 评估效果
acc_count = accuracy_score(test_target, y_pred_count)
acc_tfidf = accuracy_score(test_target, y_pred_tfidf)

print(f"词频特征-朴素贝叶斯准确率：{acc_count:.4f}")
print(f"TF-IDF特征-朴素贝叶斯准确率：{acc_tfidf:.4f}")

# 5. 可视化对比
fig, axes = plt.subplots(1, 2, figsize=(18, 8))

# 准确率对比
models = ['词频特征', 'TF-IDF特征']
accuracies = [acc_count, acc_tfidf]
axes[0].bar(models, accuracies, color=['orange', 'green'])
axes[0].set_ylim(0, 1.1)  # 调整y轴范围，让文本显示更清晰
axes[0].set_ylabel('准确率')
axes[0].set_title('垃圾邮件检测-不同特征提取方式准确率对比')
for i, acc in enumerate(accuracies):
    axes[0].text(i, acc + 0.02, f'{acc:.4f}', ha='center', fontsize=12)

# 混淆矩阵（TF-IDF模型）
cm = confusion_matrix(test_target, y_pred_tfidf)
sns.heatmap(cm, annot=True, fmt='d', cmap='Blues', ax=axes[1],
            xticklabels=target_names, yticklabels=target_names)
axes[1].set_xlabel('预测类别', fontsize=10)
axes[1].set_ylabel('真实类别', fontsize=10)
axes[1].set_title('TF-IDF特征-朴素贝叶斯混淆矩阵', fontsize=12)
# 旋转x轴标签，避免重叠
axes[1].tick_params(axis='x', rotation=45)

plt.tight_layout()
plt.show()

3.5.3 车牌定位与识别（简化版）

基于监督学习的图像分类，模拟车牌字符识别任务。

完整代码
复制代码 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 1. 加载手写数字数据集（模拟车牌字符）
digits = load_digits()
X = digits.images  # 8x8像素的数字图像
y = digits.target  # 数字标签（0-9）

# 2. 数据预处理：将2D图像转为1D特征
X_flatten = X.reshape((len(X), -1))

# 3. 数据划分
X_train, X_test, y_train, y_test, X_img_train, X_img_test = train_test_split(
    X_flatten, y, X, test_size=0.2, random_state=42
)

# 4. 训练SVM模型
svm = SVC(kernel='rbf', gamma=0.001, random_state=42)
svm.fit(X_train, y_train)

# 5. 预测
y_pred = svm.predict(X_test)

# 6. 输出评估报告
print("车牌字符识别（数字）模型报告：")
print(classification_report(y_test, y_pred))

# 7. 可视化：原始图像 vs 预测结果
fig, axes = plt.subplots(2, 5, figsize=(12, 6))
axes = axes.ravel()

# 随机选10个测试样本
np.random.seed(42)
random_idx = np.random.choice(len(X_test), 10, replace=False)

for i, idx in enumerate(random_idx):
    axes[i].imshow(X_img_test[idx], cmap='gray')
    axes[i].set_title(f'真实：{y_test[idx]}\n预测：{y_pred[idx]}')
    axes[i].axis('off')

plt.suptitle('车牌字符识别：原始图像 vs 预测结果')
plt.tight_layout()
plt.show()

# 可视化混淆矩阵
plt.figure(figsize=(10, 8))
cm = confusion_matrix(y_test, y_pred)
plt.imshow(cm, interpolation='nearest', cmap='Blues')
plt.title('车牌字符识别-混淆矩阵')
plt.colorbar()
tick_marks = np.arange(10)
plt.xticks(tick_marks, range(10))
plt.yticks(tick_marks, range(10))
plt.xlabel('预测标签')
plt.ylabel('真实标签')

# 在混淆矩阵上标注数值
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
    for j in range(cm.shape[1]):
        plt.text(j, i, format(cm[i, j], 'd'),
                 ha="center", va="center",
                 color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.show()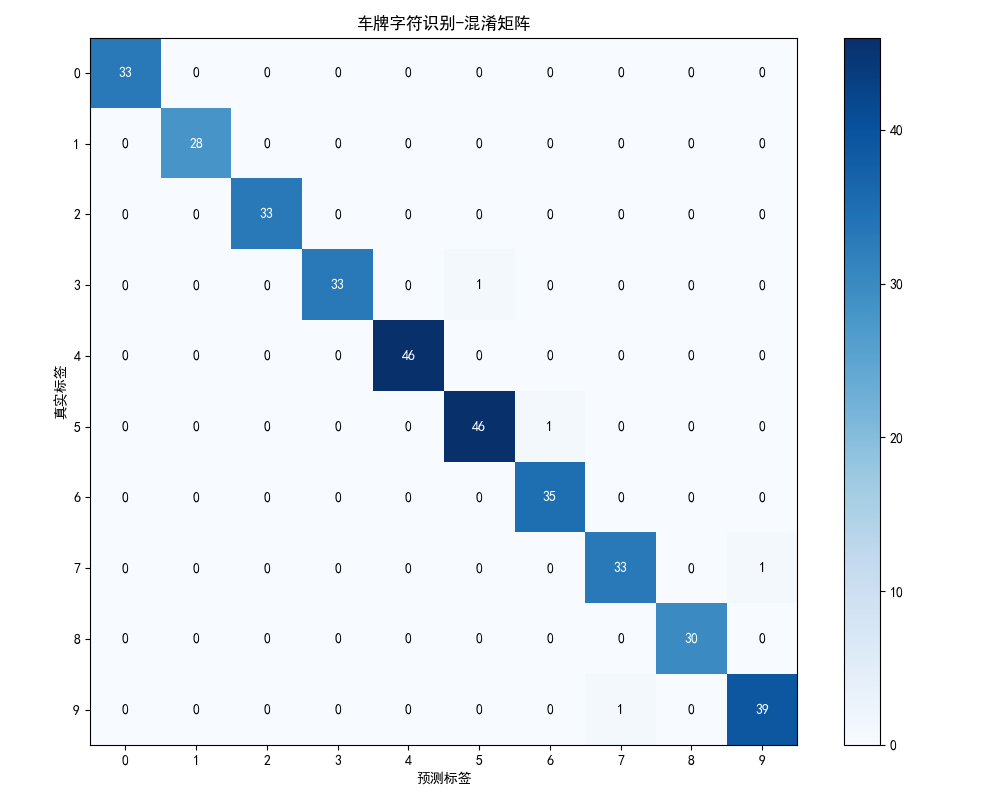

3.6 习题

基础题

  1. 简述线性回归和逻辑回归的核心区别，并用代码实现两者的效果对比。
  2. 决策树的过拟合如何解决？修改 3.2.3 中的代码，添加剪枝参数（如 min_samples_split），对比剪枝前后的效果。
  3. 朴素贝叶斯的 "朴素" 体现在哪里？为什么朴素贝叶斯适合文本分类？

进阶题

  1. 基于 3.5.1 的信用风险评估代码，尝试使用不同的模型（如逻辑回归、SVM），对比各模型的效果。
  2. 基于 3.5.2 的垃圾邮件检测代码，添加自定义的垃圾邮件关键词特征，提升模型准确率。
  3. 基于 3.5.3 的车牌识别代码，尝试使用 CNN（卷积神经网络）替换 SVM，对比识别效果。

流程图

总结

  1. 核心模型特点：线性模型简单易解释，决策树非线性拟合能力强，贝叶斯模型能给出概率 / 不确定性，SVM 通过核函数处理非线性数据效果优。
  2. 可视化关键：所有代码均包含对比图（原始数据 / 不同模型 / 不同参数），直观展示算法效果差异，帮助理解核心概念。
  3. 实战应用：覆盖信用风险、垃圾邮件、车牌识别三大典型监督学习场景，代码可直接运行，新手可快速上手修改和扩展。

如果觉得本文有帮助，欢迎点赞、收藏、关注～有任何问题，评论区交流！

相关推荐
明月醉窗台2 小时前
Ryzen AI --- AMD XDNA架构的部署框架
人工智能·opencv·目标检测·机器学习·计算机视觉·架构
Java程序员威哥2 小时前
用Java玩转机器学习：协同过滤算法实战（比Python快3倍的工程实现）
java·开发语言·后端·python·算法·spring·机器学习
Lips6112 小时前
第六章 支持向量机
算法·机器学习·支持向量机
一条闲鱼_mytube2 小时前
智能体设计模式（五）人机协同-知识检索RAG-智能体间通信
网络·人工智能·设计模式
雨大王5122 小时前
工业AI大模型在汽车制造中的应用：如何选择最适合的解决方案？
人工智能
AC赳赳老秦2 小时前
Kubernetes 与 DeepSeek：高效 Pod 部署配置与资源调度优化指南
人工智能·云原生·容器·kubernetes·自动化·notepad++·deepseek
sjg200104142 小时前
GoFrame学习随便记3（待续）
学习
OpenCSG2 小时前
兼顾开源创新与数据安全：CSGHub 为企业 AI 选型提供最优解
人工智能·开源
AI工具测评大师2 小时前
如何有效降低英文文本的Turnitin AI检测率？安全指南与工具推荐
人工智能·深度学习·自然语言处理·文心一言·ai写作·ai自动写作
热门推荐
01GitHub 镜像站点02OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)032025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）04UV安装并设置国内源05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08BongoCat - 跨平台键盘猫动画工具09Claude Code Skills 实用使用手册10Linux下V2Ray安装配置指南