数据结构基础：二叉树高效数据结构的奥秘

1、什么是树？

树是一种非线性的数据结构，它模仿了自然界中树的层级结构。最常见的例子就是家族的族谱或者公司的组织架构图。

与数组、链表这类将数据"一条线"串起来的线性结构不同，树结构能够非常高效地表示数据的层级关系和分组关系。

为什么需要树结构？
想象一下，如果我们要在一个拥有数百万用户的系统中查找某个特定用户。如果用数组或链表，最坏的情况下我们需要从头到尾检查每一个用户，时间复杂度是O(n)。但如果我们将用户数据组织成一棵有序的树（比如后面会讲到的二叉搜索树），查找时间可以缩短到O(log n)，效率天差地别。对于大数据量，这种效率提升是革命性的。

2、二叉树的定义和基本术语

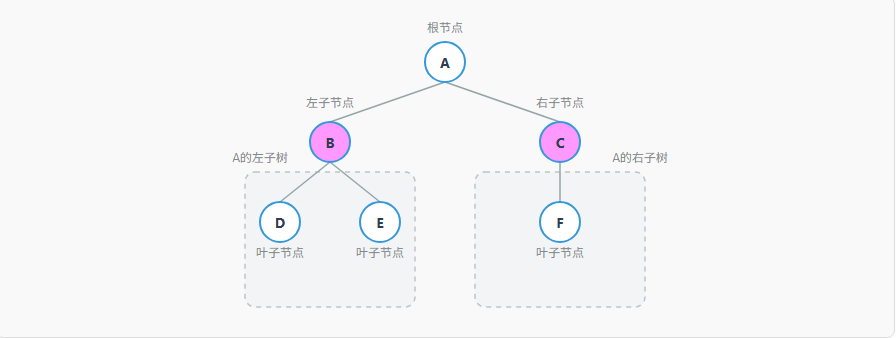
二叉树（Binary Tree） 是树结构中最简单且最常用的一种。它的核心特点是：每个节点最多有两个子节点，分别称为"左子节点"和"右子节点"。

术语	定义	示例说明
节点	树的基本组成部分，包含数据和指向其他节点的指针。
根节点	树的顶部节点，没有父节点	上图中的节点A
父节点	一个节点的上级节点	如A是B和C的父节点
子节点	一个节点的下级节点	如B和C是A的子节点
兄弟节点	拥有相同父节点的节点	如B和C是兄弟节点
叶子节点	没有子节点的节点	上图中的节点D、E、F
子树	以某个节点的子节点为根构成的树	整个以B为根的部分就是A的左子树
路径	从一个节点到另一个节点所经过的节点序列。
深度	从根节点到某节点的路径长度	根节点的深度为0。
高度	从某节点到叶子节点的最长路径	根节点A的高度为2
节点的度	一个节点拥有的子树的个数。在二叉树中，节点的度只能是0、1或2。	上图中，A和B的度为2，C的度为1，D、E、F的度为0。

二叉树的五种基本形态

从结构上讲，任何复杂的二叉树都是由以下五种最基本的形态（或者说是它们的组合）构成的。它们是二叉树的"原子"结构。

3、二叉树的种类

根据结构的不同，二叉树又可以细分为几种特殊的类型。

3.1、满二叉树

在一棵满二叉树中，除了叶子节点外，每个节点都有两个子节点。也就是说，所有节点的度（子节点数量）要么是0，要么是2。

通俗理解： 想象一个"要求严格"的家庭，每个家庭成员（节点）要么一个孩子都没有（成为叶子节点），要么就必须生两个孩子凑成"好"字。绝对不允许只生一个孩子的情况出现。

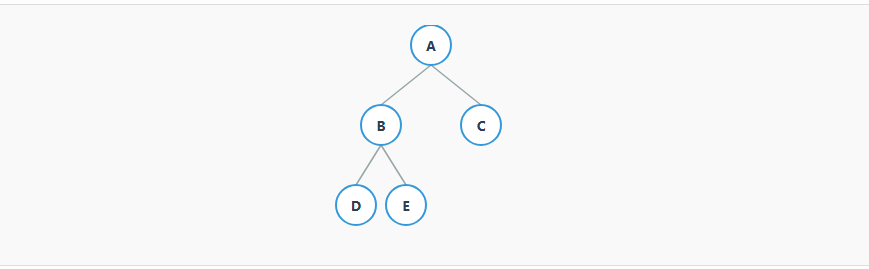
这种结构非常规整，性质也很简单。它为我们理解更复杂的树结构（如完全二叉树）打下了基础。

3.2、完全二叉树

一棵完全二叉树，除了最后一层外，其他各层节点数都达到最大，并且最后一层的节点都从左到右连续排列。满二叉树是一种特殊的完全二叉树。

通俗理解： 想象一下往一个空的书架上放书，你肯定会从最高层开始，从左到右 一本一本地放满，然后再去放下一层。完全二叉树的节点排列就是这个规则：层层都尽量填满，最后一层的书必须从最左边开始连续摆放，中间不能有空位。

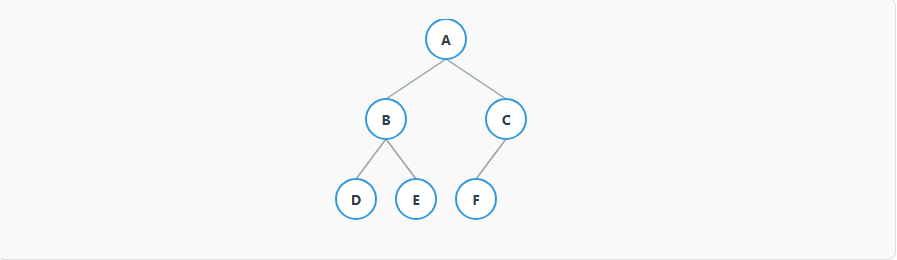
上图就是一棵完全二叉树。如果节点F不存在，而C有一个右子节点G，那么它就不是完全二叉树，因为最后一层的节点不是从左到右连续的。

完全二叉树它有一个极其重要的特性：可以用数组来存储和表示，而不需要指针。数组的索引和树的节点可以完美对应。比如，一个节点的索引为 i，那么它的左子节点索引就是 2*i+1，右子节点是 2*i+2。这使得它成为实现堆这种数据结构的不二之选，像堆排序、优先队列等高效算法都依赖于此。

3.3、完美二叉树

它是一棵满二叉树，并且所有叶子节点都在同一层。这是一种最理想、最平衡的形态。

通俗理解： 这是最"强迫症"的一种树，它既要满足满二叉树的"生就生俩"的规则，又要所有叶子节点（没有孩子的节点）都必须在同一层。最终形态是一个完美的、稳固的三角形。

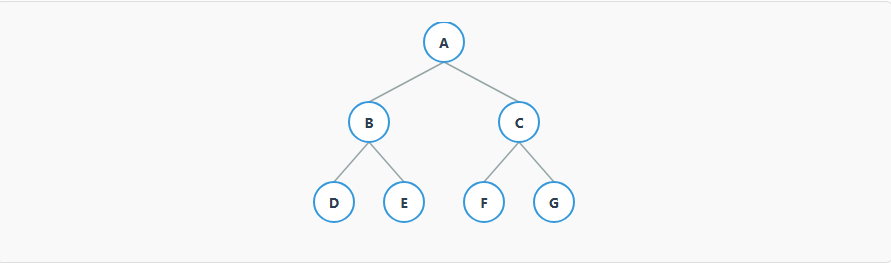
3.4、关系总结

这三者的关系可以用一句话总结：完美二叉树是最严格的，它既是满二叉树，也是完全二叉树。

• 一个完美 的，必然是满 的，也必然是完全的。
• 一个完全 的，不一定是满的。（比如3.2的例子，节点C只有一个孩子，不"满"）
• 一个满 的，也不一定是完全的。（比如3.1的例子，如果节点C也有两个孩子，但B的右孩子E没有，就不"完全"了）

特征 / 对比	满二叉树 ("不生则已，一鸣惊人")	完全二叉树 ("排队要紧凑")	完美二叉树 ("整齐划一")
节点的孩子数	要么0个，要么2个	0, 1, 或 2个都可以	要么0个，要么2个
最后一层	无特殊要求	必须从左到右连续	必须是满的
叶子节点位置	可以在不同层级	集中在最后两层	必须在同一层级
总体形态	不一定规整	比较紧凑	完美的三角形

4、二叉树的重要性质

二叉树有一些重要的数学性质，理解它们有助于我们进行算法分析。

• 性质1 : 在二叉树的第 i 层（根节点为第0层），最多有 2\^i 个节点。
• 性质2 : 高度为 h 的二叉树，最多有 2\^{h+1}-1 个节点。
• 性质3 : 对于任何一棵非空二叉树，如果叶子节点数为 n0，度为2的节点数为 n2，则 n0 = n2 + 1。

接下来我们从数学的角度证明一下n0 = n2 + 1这个等式。

我们先准备几个变量：

• N: 树中的总节点数
• E: 树中的总边数
• n0: 度为0的节点数（叶子节点）
• n1: 度为1的节点数（只有一个孩子的节点）
• n2: 度为2的节点数（有两个孩子的节点）

很显然，树的总节点数 N = n0 + n1 + n2。

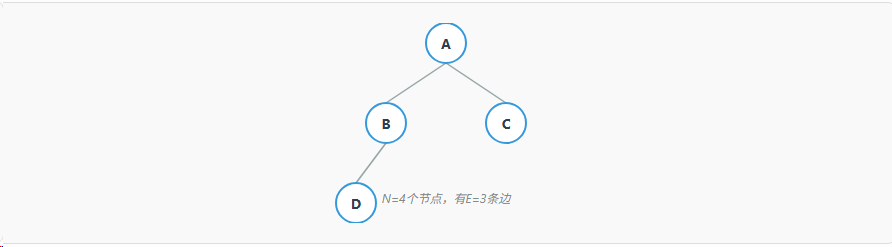
• 第一步：从"孩子"的角度数边
  • 在一棵树中，除了根节点没有"父亲"之外，其他每一个节点都有且仅有一条来自其父节点的边指向它。
  • 如果总共有 N 个节点，那么就有 N-1 个节点拥有父节点，也就意味着有 N-1 条边。 所以，我们得到了第一个关于边的公式：
  • **E = N - 1**
• 第二步：从"父亲"的角度数边
  • 边是从父节点"长出来"指向子节点的。
    • 叶子节点 (n0 类) 不会长出任何边。
    • 只有一个孩子的节点 (n1 类) 会长出 1 条边。
    • 有两个孩子的节点 (n2 类) 会长出 2 条边。
  • 所以，把所有节点长出的边加起来，就是总边数 E。 我们得到了第二个关于边的公式：
  • E = (n1 * 1) + (n2 * 2)
• 第三步：让两个公式"相遇"
  • 既然两个公式计算的都是总边数 E，那么它们必然相等： N - 1 = n1 + 2*n2
  • 现在，我们把 N = n0 + n1 + n2 这个关系代入上面的等式中： (n0 + n1 + n2) - 1 = n1 + 2*n2
• 第四步：化简
  • 这是一个简单的代数化简，我们一步步来：
  • 等式两边都有 n1，直接消掉： n0 + n2 - 1 = 2*n2
  • 把等式左边的 n2 移到右边（两边同时减去 n2）： n0 - 1 = 2*n2 - n2``n0 - 1 = n2
  • 把 -1 移到右边，整理一下： **n0 = n2 + 1**

这个结论在很多算法问题中都有妙用。

5、二叉树的实现

我们通常使用一个类来表示树的节点，节点内部包含数据和指向左右子节点的引用。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


# 定义二叉树节点
class TreeNode:
    def __init__(self, value):
        self.val = value  # 节点存储的值
        self.left = None  # 左子节点引用
        self.right = None # 右子节点引用


# 创建一棵简单的树
#      1
#     / \
#    2   3
#   / \
#  4   5
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)

print("根节点的值:", root.val)
print("根节点的左子节点的值:", root.left.val)
print("根节点的左子节点的右子节点的值:", root.left.right.val)

# 根节点的值: 1
# 根节点的左子节点的值: 2
# 根节点的左子节点的右子节点的值: 5

6、二叉树的遍历

遍历是指按照某种特定的顺序访问树中的所有节点，并且每个节点只被访问一次。这是二叉树所有操作的基础。遍历主要分为深度优先搜索（DFS）和广度优先搜索（BFS）两大类。

遍历的本质是"以某种顺序访问所有节点"。不同顺序产生不同的结构化信息，因此用途不同。

为了方便理解，我们用下面这棵树作为所有遍历方法的示例：

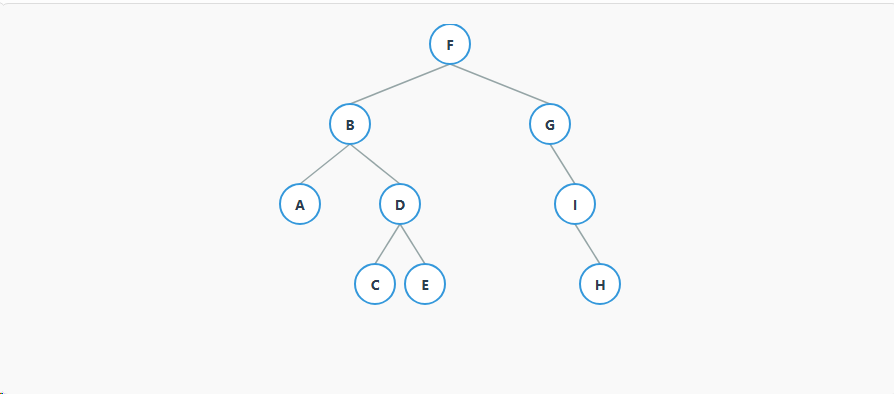
6.1、深度优先搜索 (DFS)

DFS会尽可能深地搜索树的分支。根据访问根节点的时机不同，DFS分为三种主要类型。

前序遍历

访问顺序：根节点 -> 左子树 -> 右子树

对于示例树，前序遍历结果是：F, B, A, D, C, E, G, I, H

def preorder_traversal(node):
    if node is None:
        return
    print(node.val, end=' ')  # 1. 访问根节点
    preorder_traversal(node.left)   # 2. 遍历左子树
    preorder_traversal(node.right)  # 3. 遍历右子树

前序遍历的一个典型应用是创建树的副本 。因为我们总是先处理根节点，可以先创建当前节点，然后递归地处理其左右子树来构建整个副本。另外，在数学表达式树中，前序遍历可以得到波兰表示法（前缀表达式）。

中序遍历

访问顺序：左子树 -> 根节点 -> 右子树

对于示例树，中序遍历结果是：A, B, C, D, E, F, G, I, H

def inorder_traversal(node):
    if node is None:
        return
    inorder_traversal(node.left)   # 1. 遍历左子树
    print(node.val, end=' ')  # 2. 访问根节点
    inorder_traversal(node.right)  # 3. 遍历右子树

中序遍历最著名的应用是在二叉搜索树（BST） 上。对一棵BST进行中序遍历，得到的结果会是一个升序排列的序列。这个特性非常关键。

后序遍历

访问顺序：左子树 -> 右子树 -> 根节点

对于示例树，后序遍历结果是：A, C, E, D, B, H, I, G, F

def postorder_traversal(node):
    if node is None:
        return
    postorder_traversal(node.left)   # 1. 遍历左子树
    postorder_traversal(node.right)  # 2. 遍历右子树
    print(node.val, end=' ')  # 3. 访问根节点

后序遍历的顺序保证了在处理一个节点之前，它的所有子节点都已经被处理完毕。这个特性使得它非常适合用来释放或销毁树的节点 ，因为你可以在删除一个节点之前安全地删除它的所有子孙。另外，它也可以用于计算逆波兰表示法（后缀表达式）。

6.2、广度优先搜索 (BFS) / 层序遍历

访问顺序：从上到下，从左到右，逐层访问

对于示例树，层序遍历结果是：F, B, G, A, D, I, C, E, H

层序遍历通常借助一个队列（Queue）来实现。

from collections import deque

def level_order_traversal(root):
    if root is None:
        return
    
    queue = deque([root]) # 使用双端队列
    
    while queue:
        node = queue.popleft() # 从队列头部取出一个节点
        print(node.val, end=' ')
        
        if node.left:
            queue.append(node.left) # 将左子节点加入队列尾部
        if node.right:
            queue.append(node.right) # 将右子节点加入队列尾部

层序遍历在寻找最短路径问题中非常有用。因为它是逐层扩展的，所以当它第一次找到目标时，所经过的路径必然是层数最少的，也就是最短的。很多图算法，如Dijkstra，都基于类似的思想。

6.3、遍历算法复杂度分析

假设树中有 N 个节点，树的高度为 H。

时间复杂度

对于我们讨论的所有四种遍历方法（前序、中序、后序、层序），时间复杂度都是 O(N)。

因为无论采用哪种顺序，每种遍历算法都必须访问树中的每一个节点且仅访问一次，才能完成整个遍历过程。因此，操作的总量与节点的数量 N 呈线性关系。

空间复杂度

空间复杂度则更有趣，因为它取决于实现方式（递归还是迭代）和树的形状。

遍历方法	实现方式	空间复杂度	原因分析
前序、中序、后序 (DFS)	递归	O(H)	空间消耗主要来自函数调用的递归栈。栈的最大深度等于树的高度 H + 最坏情况: 树退化成一个链表，高度 H = N，空间复杂度为 O(N) 。 + 最好情况: 树是完美平衡的，高度 H = log(N)，空间复杂度为 O(log N)。
层序遍历 (BFS)	迭代 + 队列	O(W)	空间消耗主要来自存储节点的队列。队列在某一时刻的最大长度取决于树的最宽层的节点数，我们称之为宽度 W + 最坏情况: 树是一个完美的完全二叉树，最后一层有大约 N/2 个节点，此时 W 约等于 N/2，空间复杂度O(N) 。 + 最好情况: 树退化成一个链表，每一层都只有一个节点，宽度 W = 1，空间复杂度为 O(1)。

虽然所有遍历方法的时间复杂度相同，但在空间使用上，深度优先遍历（递归）在树极度不平衡时可能导致栈溢出，而广度优先遍历则在树"矮胖"时会消耗更多内存。这是在选择具体遍历策略时需要考虑的权衡。

6.4、可视化演示

https://code.juejin.cn/pen/7554232474402816000?embed=true)

7、Python实现二叉树

下面是一个完整的Python类，它封装了二叉树的节点、构建、遍历

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from collections import deque


# 1. 定义树节点类
class TreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None


# 2. 完整的二叉树操作类
class BinaryTree:
    def __init__(self, root_node=None):
        self.root = root_node

    # --- 遍历方法 ---
    def preorder_traversal(self):
        result = []
        self._preorder_recursive(self.root, result)
        return result

    def _preorder_recursive(self, node, result):
        if node is None:
            return
        result.append(node.val)
        self._preorder_recursive(node.left, result)
        self._preorder_recursive(node.right, result)

    def inorder_traversal(self):
        result = []
        self._inorder_recursive(self.root, result)
        return result

    def _inorder_recursive(self, node, result):
        if node is None:
            return
        self._inorder_recursive(node.left, result)
        result.append(node.val)
        self._inorder_recursive(node.right, result)

    def postorder_traversal(self):
        result = []
        self._postorder_recursive(self.root, result)
        return result

    def _postorder_recursive(self, node, result):
        if node is None:
            return
        self._postorder_recursive(node.left, result)
        self._postorder_recursive(node.right, result)
        result.append(node.val)

    def level_order_traversal(self):
        if self.root is None:
            return []
        
        queue = deque([self.root])
        result = []
        while queue:
            node = queue.popleft()
            result.append(node.val)
            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)
        return result

    def print_tree(self):
        print("--- 树的结构可视化 (横向) ---")
        if self.root is None:
            print("(空树)")
        else:
            self._print_recursive(self.root)
        print("---------------------------------")
    
    def _print_recursive(self, node, prefix="", is_left=True):
        if node.right:
            self._print_recursive(node.right, prefix + ("│   " if is_left else "    "), False)

        print(prefix + ("└── " if is_left else "┌── ") + str(node.val))

        if node.left:
            self._print_recursive(node.left, prefix + ("    " if is_left else "│   "), True)


def build_example_tree():
    F = TreeNode('F')
    B = TreeNode('B')
    G = TreeNode('G')
    A = TreeNode('A')
    D = TreeNode('D')
    I = TreeNode('I')
    C = TreeNode('C')
    E = TreeNode('E')
    H = TreeNode('H')

    F.left = B
    F.right = G
    B.left = A
    B.right = D
    D.left = C
    D.right = E
    G.right = I # I是G的右子节点
    I.right = H # H是I的右子节点
    
    return F


if __name__ == "__main__":
    # 创建节点并构建树
    example_root = build_example_tree()
    
    # 将树的根节点交给BinaryTree类管理
    tree = BinaryTree(example_root)
    
    # 可视化打印树的结构
    tree.print_tree()
    
    # 执行并打印各种遍历结果
    preorder_res = tree.preorder_traversal()
    print(f"前序遍历 (根-左-右): {' -> '.join(preorder_res)}")
    
    inorder_res = tree.inorder_traversal()
    print(f"中序遍历 (左-根-右): {' -> '.join(inorder_res)}")

    postorder_res = tree.postorder_traversal()
    print(f"后序遍历 (左-右-根): {' -> '.join(postorder_res)}")
    
    levelorder_res = tree.level_order_traversal()
    print(f"层序遍历 (逐层):   {' -> '.join(levelorder_res)}")

#   --- 树的结构可视化 (横向) ---
# │           ┌── H
# │       ┌── I
# │   ┌── G
# └── F
#     │       ┌── E
#     │   ┌── D
#     │   │   └── C
#     └── B
#         └── A
# ---------------------------------
# 前序遍历 (根-左-右): F -> B -> A -> D -> C -> E -> G -> I -> H
# 中序遍历 (左-根-右): A -> B -> C -> D -> E -> F -> G -> I -> H
# 后序遍历 (左-右-根): A -> C -> E -> D -> B -> H -> I -> G -> F
# 层序遍历 (逐层):   F -> B -> G -> A -> D -> I -> C -> E -> H

8、重要应用：二叉搜索树（BST）

二叉搜索树（Binary Search Tree），也叫二叉排序树，是一种特殊的二叉树。它满足以下性质：

1. 对于树中的任意节点，其左子树中所有节点的值都小于该节点的值。
2. 其右子树中所有节点的值都大于该节点的值。
3. 它的左右子树也分别为二叉搜索树。

这个特性每个节点满足"左子树所有节点值 < 根 < 右子树所有节点值"。这使得查找/插入/删除都能沿着单一路径进行，平均时间复杂度接近 O(log n)。

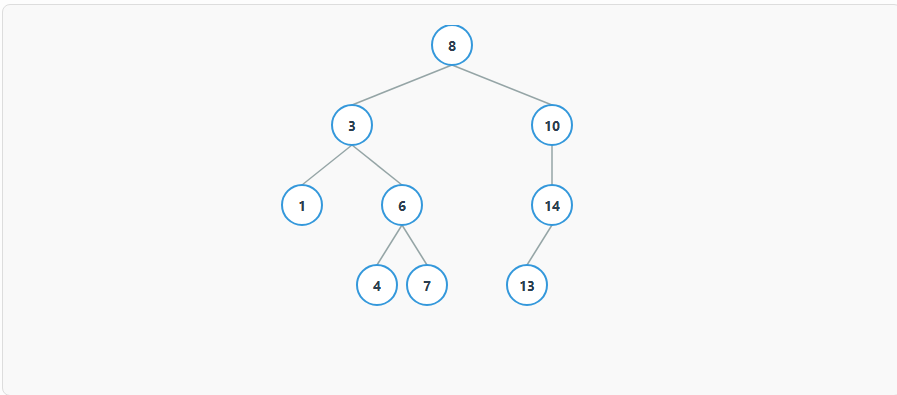
8.1、查找操作

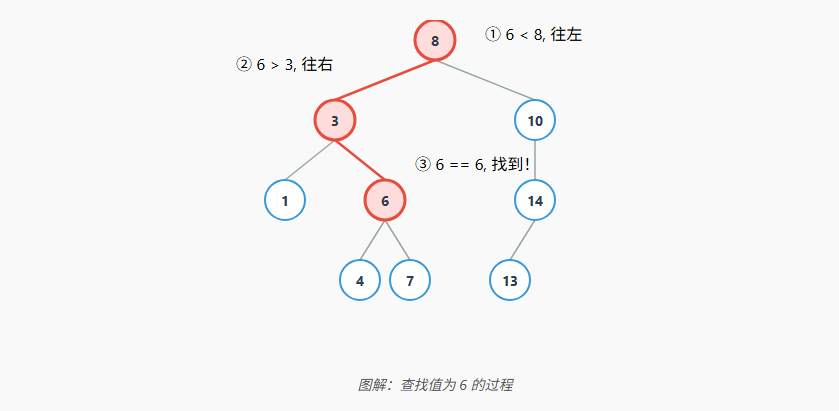
查找过程利用了BST的排序特性，每次比较都能排除掉一半的节点，非常高效。从根节点开始：

• 如果目标值等于当前节点值，查找成功。
• 如果目标值小于当前节点值，则在左子树中继续查找。
• 如果目标值大于当前节点值，则在右子树中继续查找。

def search_bst(root, target):
    node = root
    while node is not None:
        if target == node.val:
            return node # 找到了
        elif target < node.val:
            node = node.left # 去左子树找
        else:
            node = node.right # 去右子树找
    return None # 没找到

8.2、插入操作

插入过程与查找类似，首先找到新值应该被插入的"空位"，然后将新节点挂载上去。

def insert_bst(root, value):
    if root is None:
        return TreeNode(value)
    
    node = root
    while True:
        if value < node.val:
            if node.left is None:
                node.left = TreeNode(value)
                return root
            node = node.left
        else: # value >= node.val, 通常BST不允许重复值, 这里简化为放右边
            if node.right is None:
                node.right = TreeNode(value)
                return root
            node = node.right

8.3 删除操作

删除操作是BST中最复杂的一环，因为它必须在删除节点后，依然维持BST的性质。我们需要分三种情况讨论：

情况1: 删除的节点是叶子节点 (度为0)

这是最简单的情况。直接找到该节点的父节点，并将父节点指向它的链接断开即可。

情况2: 删除的节点只有一个子节点 (度为1)

这种情况也比较简单。将该节点的父节点，直接链接到该节点的那个唯一的子节点上，相当于"跳过"了被删除的节点。

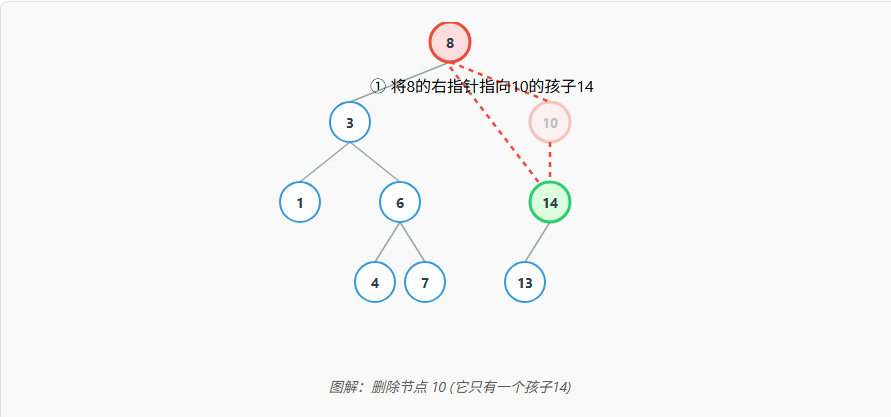
情况3: 删除的节点有两个子节点 (度为2)

这是最复杂的情况。我们不能简单地删除它，因为会留下两个"孤儿"子树。**核心思想是：**在不破坏BST性质的前提下，找一个节点来"顶替"被删除节点的位置。

这个"顶替者"有两个选择：

1. 中序后继 : 从被删除节点的右子树 中，找到值最小的那个节点。
2. 中序前驱 : 从被删除节点的左子树 中，找到值最大的那个节点。

我们以最常用的中序后继 为例，分步图解删除节点 3 的过程：

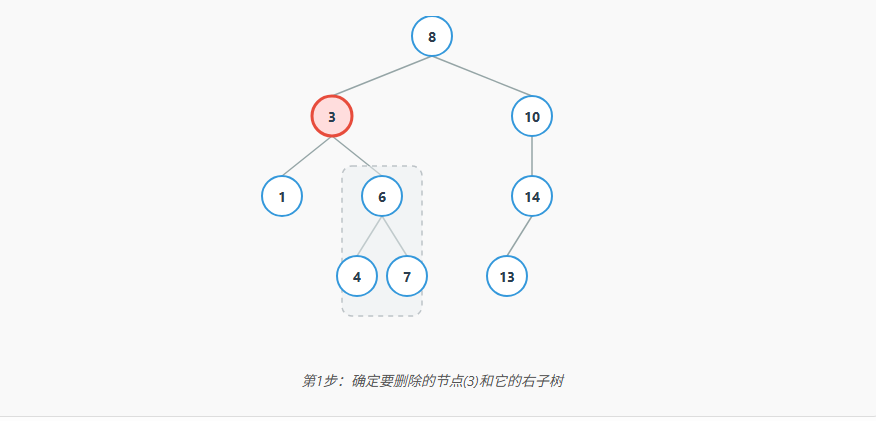
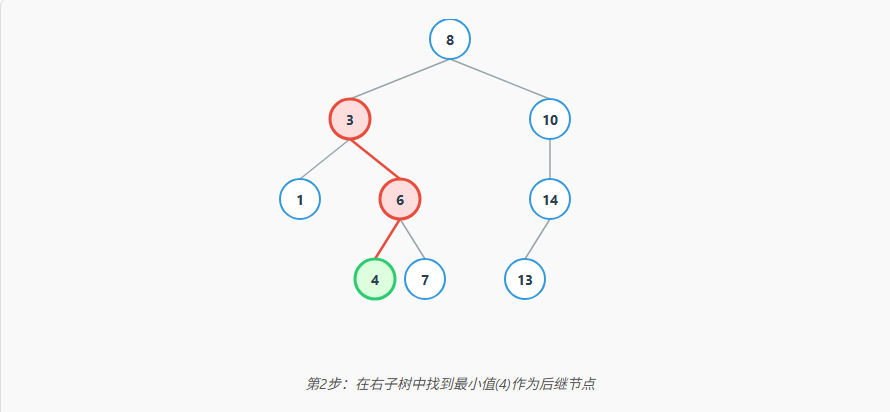
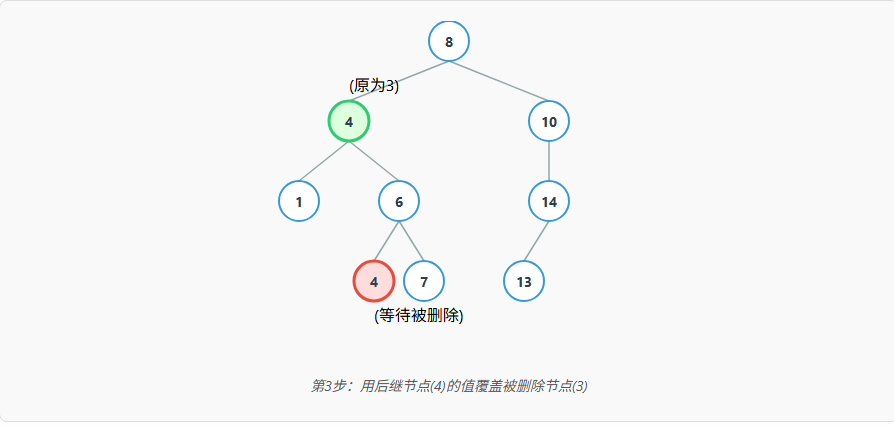
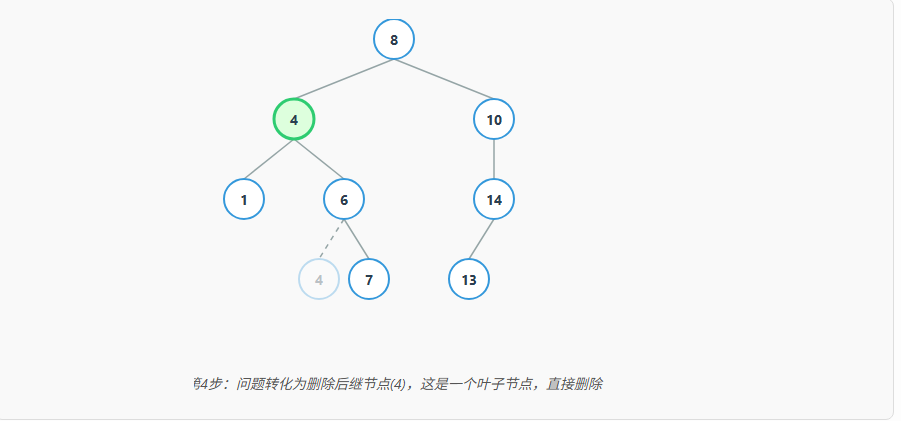
通过这个转换，我们就把一个复杂问题（删除有两个孩子的节点）转化成了一个简单问题（删除叶子节点或只有一个孩子的节点）。

def delete_bst_node(root, key):
    if not root: # 如果树为空，直接返回
        return root

    if key < root.val: # 如果key在左子树
        root.left = delete_bst_node(root.left, key)
    elif key > root.val: # 如果key在右子树
        root.right = delete_bst_node(root.right, key)
    else: # 找到了要删除的节点
        # 情况1: 是叶子节点 或 只有一个右孩子
        if not root.left:
            return root.right
        # 情况2: 只有一个左孩子
        elif not root.right:
            return root.left
        
        # 情况3: 有两个孩子
        # 找到右子树中的最小节点 (中序后继)
        temp = root.right
        while temp.left:
            temp = temp.left
        
        # 用后继节点的值覆盖当前节点
        root.val = temp.val
        
        # 递归地在右子树中删除那个后继节点
        root.right = delete_bst_node(root.right, root.val)
        
    return root

8.4、致命缺点

如果插入的数据是有序的 （例如：1, 2, 3, 4, 5），BST会退化成一个链表。

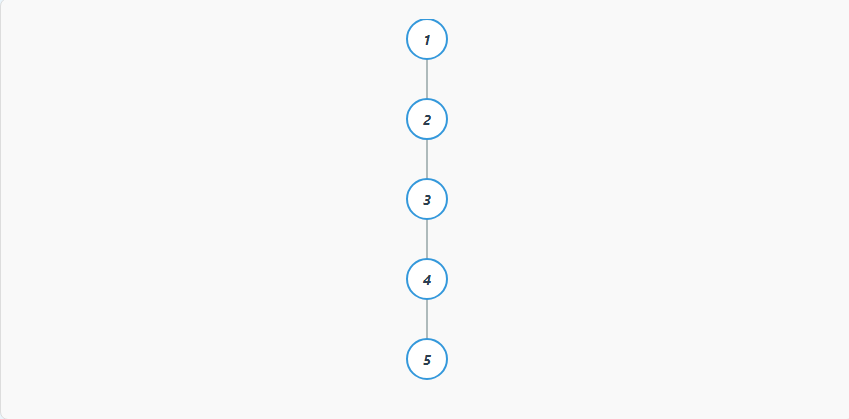
在这种情况下，所有操作的时间复杂度都会从O(log n)恶化到O(n)，失去了树结构的优势。 如何解决？ 这就是平衡二叉搜索树（如AVL树、红黑树）存在的意义。它们通过在插入和删除后进行"旋转"等操作，强制维持树的平衡，从而保证在任何情况下操作的时间复杂度都为O(log n)。这部分内容更为复杂，但其根源就是为了解决BST的不平衡问题。

8.5、完整代码实现

下面是一个完整的Python类，它封装了二叉搜索树的所有核心操作。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


class TreeNode:
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None


class BinarySearchTree:
    def __init__(self):
        self.root = None

    # --- 插入操作 ---
    def insert(self, value):
        # 如果是空树，新节点就是根
        if self.root is None:
            self.root = TreeNode(value)
        else:
            # 否则，调用递归辅助函数
            self._insert_recursive(self.root, value)
    
    def _insert_recursive(self, node, value):
        if value < node.val:
            if node.left is None:
                node.left = TreeNode(value)
            else:
                self._insert_recursive(node.left, value)
        elif value > node.val: # BST 通常不允许重复值
            if node.right is None:
                node.right = TreeNode(value)
            else:
                self._insert_recursive(node.right, value)

    # --- 查找操作 ---
    def search(self, value):
        return self._search_recursive(self.root, value)

    def _search_recursive(self, node, value):
        # 递归终止条件：找到节点或遍历到空
        if node is None or node.val == value:
            return node
        # 根据大小关系，决定去左子树还是右子树
        if value < node.val:
            return self._search_recursive(node.left, value)
        else:
            return self._search_recursive(node.right, value)
            
    # --- 删除操作 ---
    def delete(self, value):
        # 删除操作会返回新的子树根节点
        self.root = self._delete_recursive(self.root, value)
        
    def _delete_recursive(self, node, key):
        # 使用之前章节讲解的递归删除逻辑
        if not node:
            return node

        if key < node.val:
            node.left = self._delete_recursive(node.left, key)
        elif key > node.val:
            node.right = self._delete_recursive(node.right, key)
        else: # 找到要删除的节点
            # 情况1或2：节点只有一个孩子或没有孩子
            if not node.left:
                return node.right
            elif not node.right:
                return node.left
            
            # 情况3：节点有两个孩子
            # 找到中序后继节点（右子树的最小值）
            successor = node.right
            while successor.left:
                successor = successor.left
            
            # 用后继节点的值替换当前节点
            node.val = successor.val
            # 递归地删除那个后继节点
            node.right = self._delete_recursive(node.right, successor.val)
            
        return node

    def print_tree(self):
        print("--- BST 结构可视化 ---")
        if self.root is None:
            print("(空树)")
        else:
            self._print_recursive(self.root)
        print("-----------------------")
    
    def _print_recursive(self, node, prefix="", is_left=True):
        if node.right:
            self._print_recursive(node.right, prefix + ("│   " if is_left else "    "), False)
        print(prefix + ("└── " if is_left else "┌── ") + str(node.val))
        if node.left:
            self._print_recursive(node.left, prefix + ("    " if is_left else "│   "), True)


if __name__ == "__main__":
    bst = BinarySearchTree()
    values_to_insert = [8, 3, 10, 1, 6, 14, 4, 7, 13]
    print(f"待插入数据: {values_to_insert}\n")
    for val in values_to_insert:
        bst.insert(val)
        
    print("--- 初始化的二叉搜索树 ---")
    bst.print_tree()
    
    print("\n--- 查找节点 6 ---")
    found_node = bst.search(6)
    print(f"结果: {'找到了！' if found_node else '未找到。'}")
        
    print("\n--- 删除叶子节点 1 ---")
    bst.delete(1)
    bst.print_tree()
    
    print("\n--- 删除只有一个孩子的节点 14 ---")
    bst.delete(14)
    bst.print_tree()

    print("\n--- 删除有两个孩子的节点 3 ---")
    bst.delete(3)
    bst.print_tree()
    
    print("\n--- 删除根节点 8 ---")
    bst.delete(8)
    bst.print_tree()
    

# 待插入数据: [8, 3, 10, 1, 6, 14, 4, 7, 13]

# --- 初始化的二叉搜索树 ---
# --- BST 结构可视化 ---
# │       ┌── 14
# │       │   └── 13
# │   ┌── 10
# └── 8
#     │       ┌── 7
#     │   ┌── 6
#     │   │   └── 4
#     └── 3
#         └── 1
# -----------------------

# --- 查找节点 6 ---
# 结果: 找到了！

# --- 删除叶子节点 1 ---
# --- BST 结构可视化 ---
# │       ┌── 14
# │       │   └── 13
# │   ┌── 10
# └── 8
#     │       ┌── 7
#     │   ┌── 6
#     │   │   └── 4
#     └── 3
# -----------------------

# --- 删除只有一个孩子的节点 14 ---
# --- BST 结构可视化 ---
# │       ┌── 13
# │   ┌── 10
# └── 8
#     │       ┌── 7
#     │   ┌── 6
#     │   │   └── 4
#     └── 3
# -----------------------

# --- 删除有两个孩子的节点 3 ---
# --- BST 结构可视化 ---
# │       ┌── 13
# │   ┌── 10
# └── 8
#     │   ┌── 7
#     └── 6
#         └── 4
# -----------------------

# --- 删除根节点 8 ---
# --- BST 结构可视化 ---
# │   ┌── 13
# └── 10
#     │   ┌── 7
#     └── 6
#         └── 4
# -----------------------

8.6、可视化演示

https://code.juejin.cn/pen/7554329133264535561?embed=true

9、平衡二叉搜索树

为了解决普通BST在最坏情况下的性能退化问题，科学家们设计了多种自平衡二叉搜索树。它们的核心思想是：在每次插入或删除节点后，通过一系列操作来检查并恢复树的平衡，确保树的高度始终保持在 O(log N) 级别，从而保证各种操作的效率。

我们以最经典的一种------AVL树为例，来深入了解其工作原理。

9.1、AVL树

AVL树得名于其发明者 Adelson-Velsky 和 Landis。它是一种严格的自平衡树，要求树中任何节点的左右子树高度差的绝对值不能超过1。

平衡因子(Balance Factor)

为了衡量节点的平衡性，我们引入了平衡因子的概念：

平衡因子 = 左子树高度 - 右子树高度

AVL树的硬性规定是：所有节点的平衡因子只能是 -1, 0, 或 1。

• 如果一个节点的平衡因子是 2，说明它的左子树比右子树高了2层，称为"左边太重"，需要调整。
• 如果一个节点的平衡因子是 -2，说明它的右子树比左子树高了2层，称为"右边太重"，需要调整。

9.2、核心操作：旋转

当插入或删除一个节点导致某个祖先节点的平衡被打破时，AVL树会通过旋转操作来恢复平衡。旋转的本质是在不破坏BST"左<根<右"性质的前提下，调整节点的位置，降低树的高度。

主要有四种导致不平衡的情况，需要通过两种单旋转和两种双旋转来解决。

情况一：左-左 (LL) -> 右旋

场景： 在新节点插入到失衡节点 (A) 的左子树 (B) 的左子树上，导致A的平衡因子变为2。

解决方法： 对失衡节点A进行一次右旋。

**右旋过程：**可以想象B是新的"轴心"，它"提"着A转上来。A下降成为B的右子节点，而B原来的右子树（如果存在）则需要"过继"给A，成为A的左子节点，以维持BST的性质。

情况二：右-右 (RR) -> 左旋

场景： 在新节点插入到失衡节点 (A) 的右子树 (B) 的右子树上，导致A的平衡因子变为-2。

解决方法： 对失衡节点A进行一次左旋。

**左旋过程：**与右旋相反，B是轴心，A下降成为B的左子节点，B原来的左子树成为A的右子节点。

情况三：左-右 (LR) -> 先左旋后右旋

场景： 在新节点插入到**失衡节点 (A) 的左子树 (B) 的右子树 ©**上，这是一个"拐弯"的情况。

**解决方法：**分两步走，先将这个LR结构转换成我们熟悉的LL结构，再进行右旋。

1. 对子节点B进行一次左旋，使其变为LL型。
2. 对失衡节点A进行一次右旋。

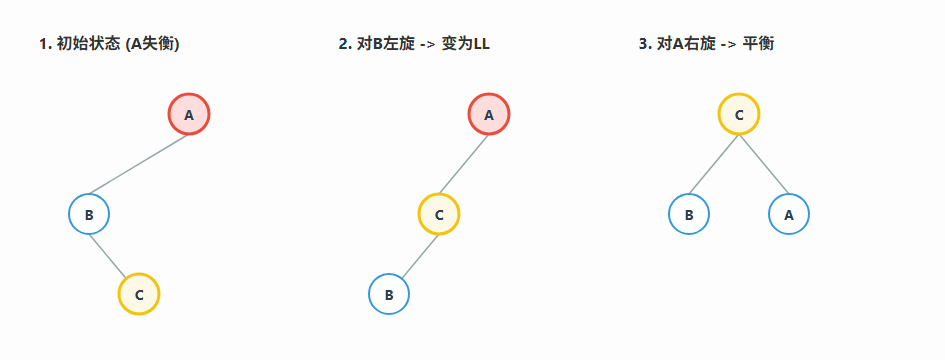
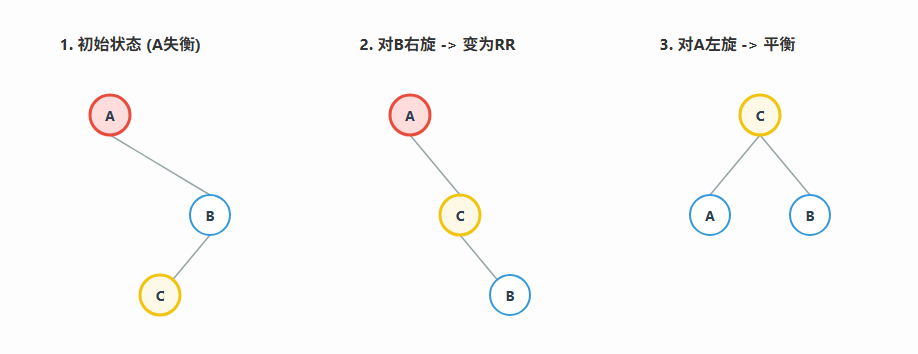
情况四：右-左 (RL) -> 先右旋后左旋

场景： 与LR对称，新节点插入到**失衡节点 (A) 的右子树 (B) 的左子树 ©**上。

**解决方法：**同样分两步，先转成RR，再左旋。

1. 对子节点B进行一次右旋。
2. 对失衡节点A进行一次左旋。

9.3、AVL树 vs. 红黑树

除了AVL树，另一种非常著名的平衡二叉搜索树是红黑树 (Red-Black Tree)。它在工程中应用更广，我们后面会单独写篇文章讲解红黑树。

一句话概括：AVL树是严格的平衡，而红黑树是大致的平衡。

• AVL树 追求极致的平衡（高度差不超过1），这使得它的查找性能非常稳定且高效 。但为了维持这种严格的平衡，它可能需要进行更频繁的旋转操作，因此在插入和删除密集型场景下开销较大。
• 红黑树 的平衡条件相对宽松，它通过节点颜色（红/黑）和五条规则来确保最长路径不超过最短路径的两倍。这意味着它能容忍一定程度的不平衡，从而减少了旋转的次数。在写操作（插入、删除）频繁的场景下，它的综合性能通常优于AVL树。

简单来说，如果你的应用场景是"查多改少"，AVL树可能是更好的选择。如果是"增删改查比较均衡"或者"改多查少"，红黑树通常表现更佳。

9.4、完整代码实现

下面是一个AVL树的完整Python实现。代码通过递归方式实现插入和自平衡。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


class AVLNode:
    """AVL 树节点类，包含值、左右子节点和高度属性。"""
    def __init__(self, value):
        self.val = value
        self.left = None
        self.right = None
        self.height = 1 # 新节点的高度初始为1



class AVLTree:
    """AVL 树实现，包含插入和旋转操作，并打印树结构。"""
    def __init__(self):
        self.root = None

    # 获取节点高度
    def getHeight(self, node):
        if not node:
            return 0
        return node.height

    # 获取平衡因子
    def getBalance(self, node):
        if not node:
            return 0
        return self.getHeight(node.left) - self.getHeight(node.right)

    # 右旋
    def rightRotate(self, z):
        y = z.left
        T3 = y.right

        # 执行旋转
        y.right = z
        z.left = T3

        # 更新高度
        z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right))
        y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right))

        # 返回新的根节点
        return y

    # 左旋
    def leftRotate(self, z):
        y = z.right
        T2 = y.left

        # 执行旋转
        y.left = z
        z.right = T2

        # 更新高度
        z.height = 1 + max(self.getHeight(z.left), self.getHeight(z.right))
        y.height = 1 + max(self.getHeight(y.left), self.getHeight(y.right))
        
        # 返回新的根节点
        return y

    # 插入操作
    def insert(self, value):
        print(f"--- 插入值: {value} ---")
        self.root = self._insert_recursive(self.root, value)
        self.print_tree()

    def _insert_recursive(self, node, value):
        # 1. 标准的BST插入
        if not node:
            return AVLNode(value)
        elif value < node.val:
            node.left = self._insert_recursive(node.left, value)
        else:
            node.right = self._insert_recursive(node.right, value)

        # 2. 更新祖先节点的高度
        node.height = 1 + max(self.getHeight(node.left), self.getHeight(node.right))

        # 3. 获取平衡因子
        balance = self.getBalance(node)

        # 4. 如果失衡，进行旋转
        # 左-左 (LL)
        if balance > 1 and value < node.left.val:
            print(f"检测到 LL 型不平衡，在节点 {node.val} 处进行右旋")
            return self.rightRotate(node)

        # 右-右 (RR)
        if balance < -1 and value > node.right.val:
            print(f"检测到 RR 型不平衡，在节点 {node.val} 处进行左旋")
            return self.leftRotate(node)

        # 左-右 (LR)
        if balance > 1 and value > node.left.val:
            print(f"检测到 LR 型不平衡，在节点 {node.left.val} 处先左旋，再在节点 {node.val} 处右旋")
            node.left = self.leftRotate(node.left)
            return self.rightRotate(node)

        # 右-左 (RL)
        if balance < -1 and value < node.right.val:
            print(f"检测到 RL 型不平衡，在节点 {node.right.val} 处先右旋，再在节点 {node.val} 处左旋")
            node.right = self.rightRotate(node.right)
            return self.leftRotate(node)

        return node
    
    # 可视化打印
    def print_tree(self):
        if self.root is None:
            print("(空树)")
        else:
            self._print_recursive(self.root)
        print("---------------------\n")

    def _print_recursive(self, node, prefix="", is_left=True):
        if node.right:
            self._print_recursive(node.right, prefix + ("│   " if is_left else "    "), False)
        print(prefix + ("└── " if is_left else "┌── ") + str(node.val))
        if node.left:
            self._print_recursive(node.left, prefix + ("    " if is_left else "│   "), True)


if __name__ == "__main__":
    avl_tree = AVLTree()
    
    # 演示一个会导致多次旋转的插入序列
    # 普通BST会退化成链表
    nodes_to_insert = [10, 20, 30, 40, 50, 25]

    for node_val in nodes_to_insert:
        avl_tree.insert(node_val)

# --- 插入值: 10 ---
# └── 10
# ---------------------

# --- 插入值: 20 ---
# │   ┌── 20
# └── 10
# ---------------------

# --- 插入值: 30 ---
# 检测到 RR 型不平衡，在节点 10 处进行左旋
# │   ┌── 30
# └── 20
#     └── 10
# ---------------------

# --- 插入值: 40 ---
# │       ┌── 40
# │   ┌── 30
# └── 20
#     └── 10
# ---------------------

# --- 插入值: 50 ---
# 检测到 RR 型不平衡，在节点 30 处进行左旋
# │       ┌── 50
# │   ┌── 40
# │   │   └── 30
# └── 20
#     └── 10
# ---------------------

# --- 插入值: 25 ---
# 检测到 RL 型不平衡，在节点 40 处先右旋，再在节点 20 处左旋
# │       ┌── 50
# │   ┌── 40
# └── 30
#     │   ┌── 25
#     └── 20
#         └── 10
# ---------------------

9.5、可视化演示

https://code.juejin.cn/pen/7555066908882501686?embed=true

10、总结

二叉树是数据结构领域一块重要的基石。它不仅本身是一种高效的数据组织方式，还衍生出了像二叉搜索树、堆、哈夫曼树（后面补充）等一系列强大的数据结构，广泛应用于数据库索引、文件系统、编译器、排序算法等众多领域。

概念	核心思想	为什么重要？
二叉树	每个节点最多两个子节点	所有复杂树结构的基础，简单且高效。
完全二叉树	节点在底层从左到右紧密排列	可以用数组高效表示，是实现"堆"的关键。
树的遍历	按特定顺序访问所有节点（前、中、后、层序）	所有树操作的基础，不同顺序有不同应用场景。
二叉搜索树(BST)	左 < 根 < 右	实现了高效的动态数据查找、插入和删除 (平均O(log n))。
平衡BST (AVL, 红黑树)	在BST基础上通过旋转等操作维持平衡	解决了BST在最坏情况下性能退化的问题，保证了任何情况都是O(log n)的性能。