Leetcode347:前K个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1：

**输入：**nums = $1,1,1,2,2,3$ , k = 2

输出： $1,2$

示例 2：

**输入：**nums = $1$ , k = 1

输出： $1$

示例 3：

**输入：**nums = $1,2,1,2,1,2,3,1,3,2$ , k = 2

输出： $1,2$

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104
k 的取值范围是 [1, 数组中不相同的元素的个数]
题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

进阶： 你所设计算法的时间复杂度必须优于 O(n log n) ，其中 n是数组大小。

非常简单，直接上代码：

java 复制代码

class Solution {
    /**解题思路：线统计每个数出现的次数，然后建立一个容量为k的小顶堆
    堆里面根据出现次数排序，如果满了并且当前要加进去的比堆顶的次数大就把最上面的弹出
    然后把当前的加进去，遍历完所有的，堆里面的就是前k个高频元素*/
    public int[] topKFrequent(int[] nums, int k) {
        if(nums.length == 1) {
            return new int[] {nums[0]};
        }
        /**定义一个hashmap，key是数字，value是数字出现的次数 */
        HashMap<Integer, Integer> countMap = new HashMap<>();
        /**遍历一遍数组统计元素出现的次数*/
        for(int num : nums) {
            countMap.put(num, countMap.getOrDefault(num, 0) + 1);
        }
        /**使用优先级队列实现一个大根堆（小顶堆） */
        PriorityQueue<int[]> heap = new PriorityQueue<>((a,b)->a[1]-b[1]);
        for(int num : countMap.keySet()) {
            int[] arr = new int[]{num, countMap.get(num)};
            /**没有满就直接放 */
            if(heap.size() < k) {
                heap.offer(arr);
            } else {
                int[] peek = heap.peek();
                if(arr[1] > peek[1]) {
                    heap.poll();
                    heap.offer(arr);
                }
            }
        }
        /**定义结果数组 */
        int[] ans = new int[k];
        int curIndex = 0;
        /**从大根堆往外拿数组填满ans */
        while(!heap.isEmpty()) {
            int[] poll = heap.poll();
            ans[curIndex ++] = poll[0];
        }
        return ans;
    }
}

我这个其实已经达到了进阶的时间复杂度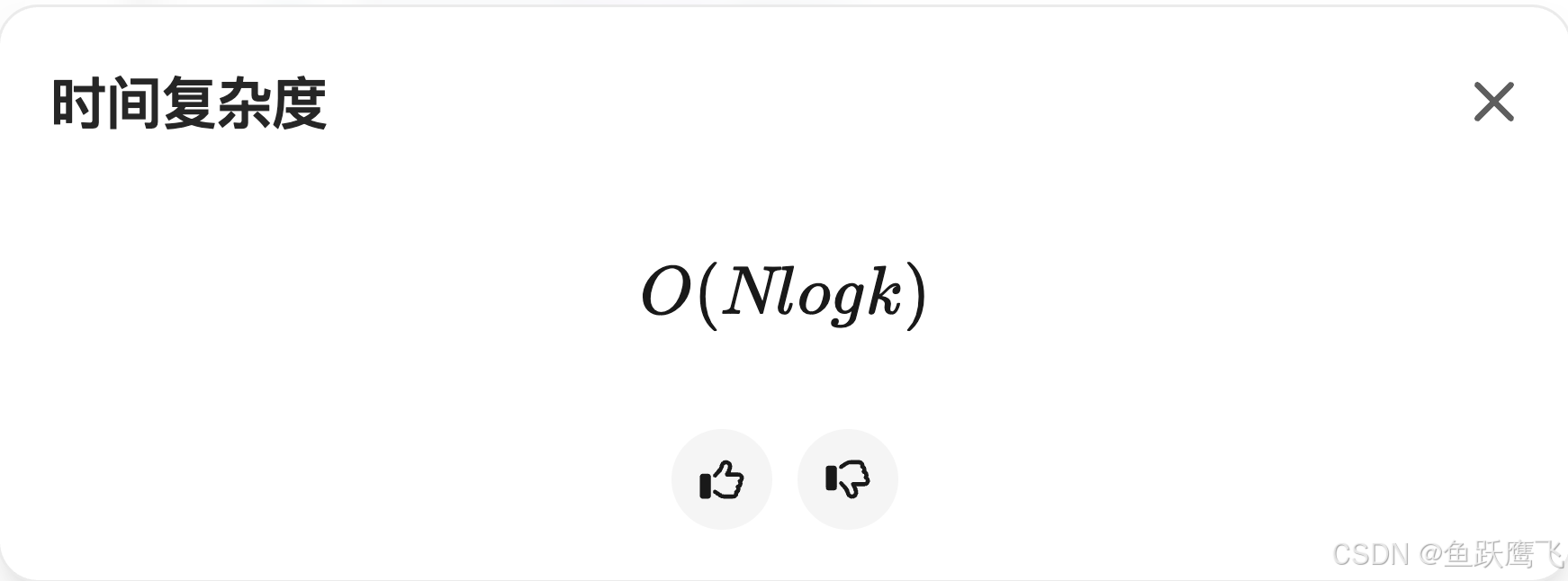

运行结果：