一、什么是单应矩阵(Homography)
一句话定义(最重要)
单应矩阵是一个 3×3 矩阵,用来描述"同一平面"在两幅图像之间的射影变换关系。
记作: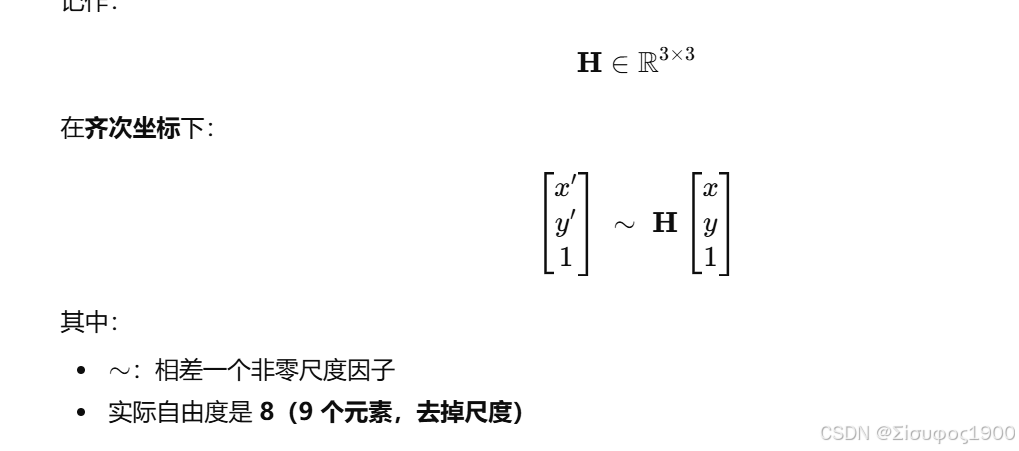
二、 特征是什么?
-
矩阵形式:是一个 3×3 的矩阵,有 9 个元素。
H=[h11h12h13h21h22h23h31h32h33]H=h11h21h31h12h22h32h13h23h33
-
齐次坐标与尺度不变性:
-
它工作在齐次坐标 下。对于一个点
p₁ = (x₁, y₁, 1)ᵀ(齐次坐标),变换后得到p₂' = H * p₁。 -
得到的
p₂' = (x₂', y₂', w)ᵀ不是直接的像素坐标,需要转换为非齐次坐标 :p₂ = (x₂'/w, y₂'/w, 1)。 -
由于齐次坐标的尺度等价性,单应矩阵
H本身也具有尺度不变性 。即,H和kH(k为非零标量)表示的是同一个几何变换。因此,H只有 8 个自由度 (通常通过令h₃₃ = 1或其他约束来固定尺度)。
-
-
点对应关系 :
给定一对匹配点
p₁ <-> p₂,其关系为: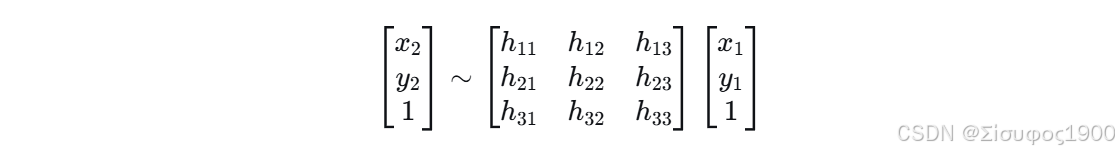
符号
~表示"在尺度意义上相等"。 -
可逆性 :如果
H是从图像1到图像2的单应,那么H⁻¹就是从图像2到图像1的单应。 -
保线性 :单应变换是一种射影变换,它保持直线的"直线性"(直线变换后仍是直线),但不一定保持平行性和长度比例。
三、单应矩阵的数学推导(从相机模型出发)
1️⃣ 针孔成像模型
空间点 X 投影到图像:
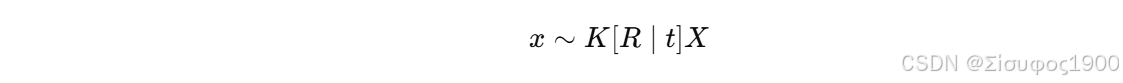
2️⃣ 点在平面上
设平面:
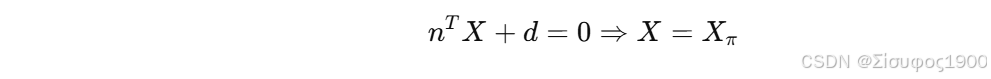
代入投影关系,可消去深度自由度。
3️⃣ 两个视角之间的关系
两幅图像的点满足:

四、单应矩阵是如何"算出来的"?
https://zhuanlan.zhihu.com/p/138266214
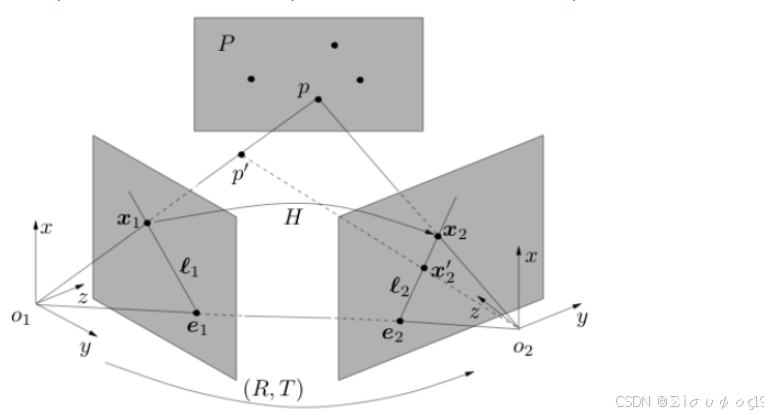
1️⃣ 基本关系
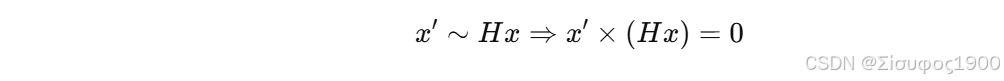
这是一个 线性约束
2️⃣ 对每一对点,得到 2 条独立方程
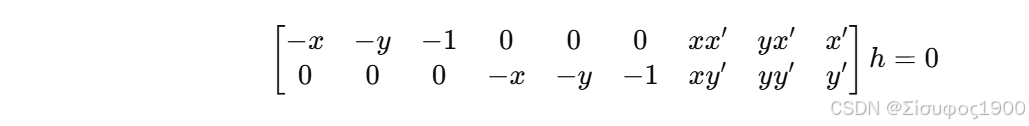
3️⃣ 堆叠成齐次线性系统
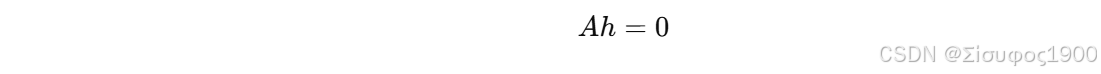
-
至少 4 对点
-
这是你熟悉的 DLT
4️⃣ 用 SVD 求解
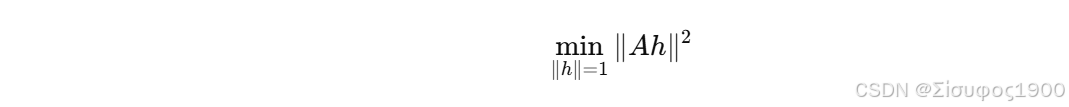
最小奇异值对应的向量
五、matlab : DLT + SVD 手写单应矩阵
cpp
% 四对平面点
pts1 = [0 0;
1 0;
1 1;
0 1];
pts2 = [100 100;
300 80;
320 300;
80 280];
A = [];
for i = 1:4
x = pts1(i,1); y = pts1(i,2);
xp = pts2(i,1); yp = pts2(i,2);
A = [A;
-x -y -1 0 0 0 x*xp y*xp xp;
0 0 0 -x -y -1 x*yp y*yp yp];
end
[~,~,V] = svd(A);
h = V(:,end);
H = reshape(h,3,3)';
H = H / H(3,3)
% 验证映射效果
p = [0.5; 0.5; 1];
p2 = H * p;
p2 = p2 / p2(3)
disp(p2(1:2))
% MATLAB 内置函数(工程推荐)
tform = fitgeotrans(pts1, pts2, 'projective');
H_matlab = tform.T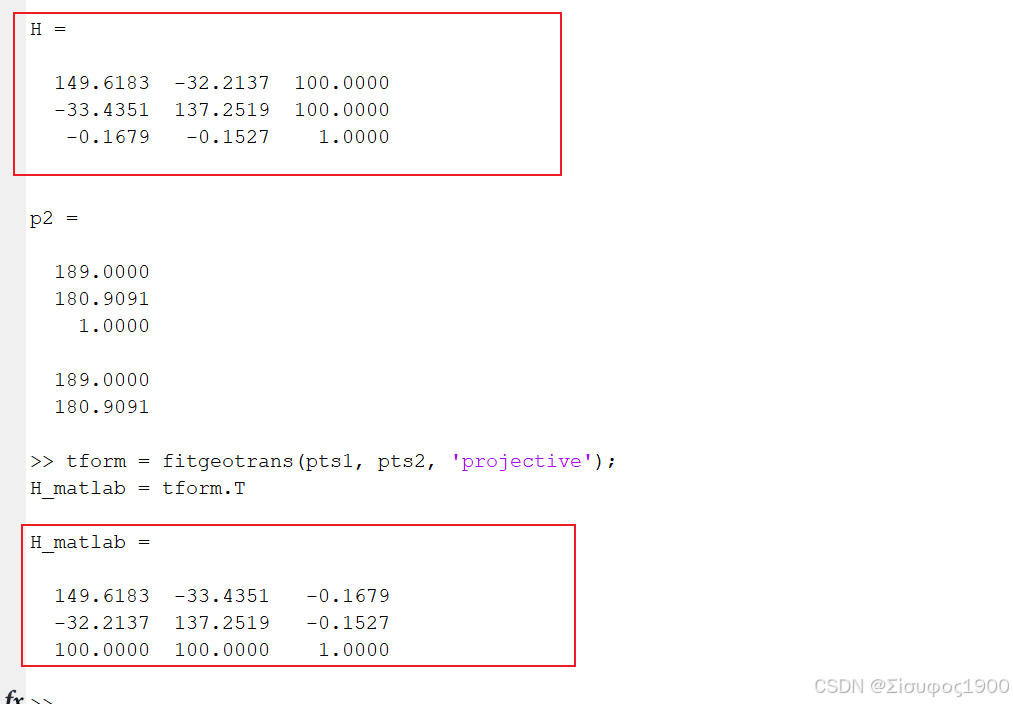
应矩阵是描述"同一平面"在两幅图像之间射影映射关系的 3×3 矩阵, 它用线性方法(DLT + SVD)求解,却表达了相机运动 + 平面几何