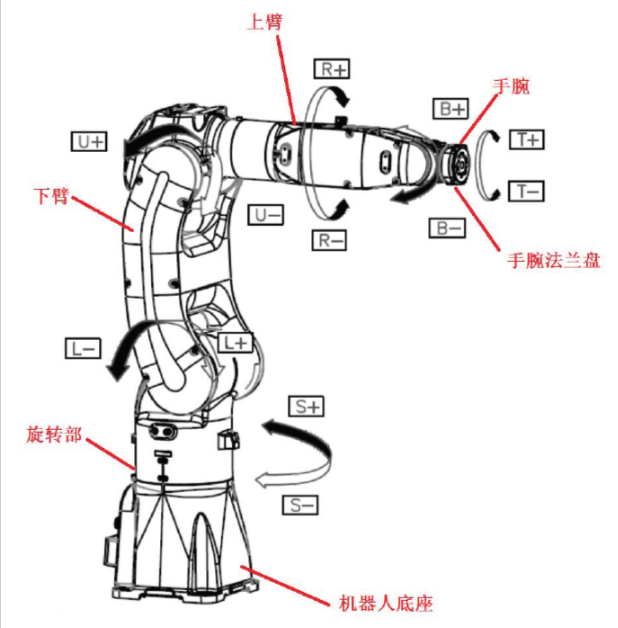
机器人学的第一部分------机器人如何理解空间:运动学与旋转矩阵
机器人学第二部分------深入旋转矩阵:轴、坐标系与坐标变换
在本系列的前两部分中,我们为理解三维空间中的旋转打下了坚实的基础。我们从将坐标系附着在机器人和工具上的概念入手,然后通过简单的几何推导,得出了绕 x、y 和 z 轴的旋转矩阵。我们了解了这些矩阵如何在不同坐标系之间转换坐标(P = R·P′),以及它们如何描述空间中向量的主动旋转。
然而,真实的机器人很少只绕单一轴旋转。机械臂、相机云台或无人机机身,通常最终会处于某种任意的姿态,而这种姿态是由若干个旋转组合而成的。
直接使用 3×3 矩阵来描述每一个姿态虽然可行,但这并不能告诉我们该姿态是如何达到的,或者该如何去控制它。
这就引出了"三角度表示法"。
在本文中,我们将:
- 利用欧拉旋转定理,理解为何任意三维旋转都可以由一系列简单的旋转组合而成;
- 介绍欧拉角的约定,重点以经典的 ZYZ 旋转为例;
- 将其与机器人学和航空航天领域更直观的横滚-俯仰-偏航 (RPY) 角度联系起来;
- 并探讨逆问题:给定一个旋转矩阵 R,我们如何反推出对应的角度?
阅读完本文后,你将能自如地在"矩阵语言"和"角度语言"之间切换:使用矩阵乘积来组合旋转,将其解释为绕特定轴的一系列旋转序列,并能从给定的旋转矩阵中提取出角度。
旋转矩阵的组合
为了处理真实的机器人,我们很少只在两个坐标系之间转换。相反,我们通常面对的是一个完整的坐标系链条:基座、关节、末端执行器、传感器等等。旋转矩阵让我们能够以一种清晰、系统化的方式沿着这条链条进行转换。
我们将使用以下符号约定:
- Pⁱ = 同一点 P 在坐标系 i 中的坐标
- Rⱼⁱ = 坐标系 j 相对于坐标系 i 的旋转矩阵
按照这个约定,
Pⁱ = Rⱼⁱ Pʲ
这句话的意思是:"取点 P 在坐标系 j 中的坐标,并将其表达在坐标系 i 中。"
1. 坐标系串联(当前坐标系视角)
考虑三个共享同一个原点的坐标系:
- 坐标系 0,其轴为 (x₀, y₀, z₀)
- 坐标系 1,其轴为 (x₁, y₁, z₁)
- 坐标系 2,其轴为 (x₂, y₂, z₂)
设 P²、P¹ 和 P⁰ 分别为同一点 P 在坐标系 2、1 和 0 中的坐标:
根据 Rⱼⁱ 的定义:
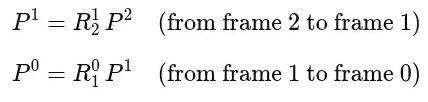
如果我们把第一个关系式代入第二个关系式中,就会得到:
P⁰ = R₁⁰ (R₂¹P²) = (R₁⁰ R₂¹)P²
因此,直接将坐标从坐标系 2 转换到坐标系 0 的旋转矩阵为:
R₂⁰ = R₁⁰ R₂¹
用通俗的话来说就是:
当每一次旋转都是相对于当前坐标系(即"动坐标系")定义时,我们在沿着坐标系链条推导时,需要通过"右乘"(后乘)各个旋转矩阵来获得总的旋转效果。
如果我们加入更多的坐标系,规律也是一样的。例如,对于坐标系 0--1--2--3:
R₃⁰ = R₂⁰ R₃² = R₁⁰ R₂¹ R₃²
通常情况下,我们通过在右侧不断乘上新的矩阵来累积旋转。
这正是正向运动学(Forward Kinematics)所采用的观点:从基座坐标系开始,依次施加旋转(稍后还会加上平移),最终到达末端执行器的坐标系。
2. 向量的连续旋转(固定坐标系视角)
还有另一种常见的情况:这次我们不再串联坐标系,而是保持一个坐标系固定不动,直接对向量本身进行多次旋转。
想象一下,在一个固定的坐标系 O--xyz 中有一个向量 P。
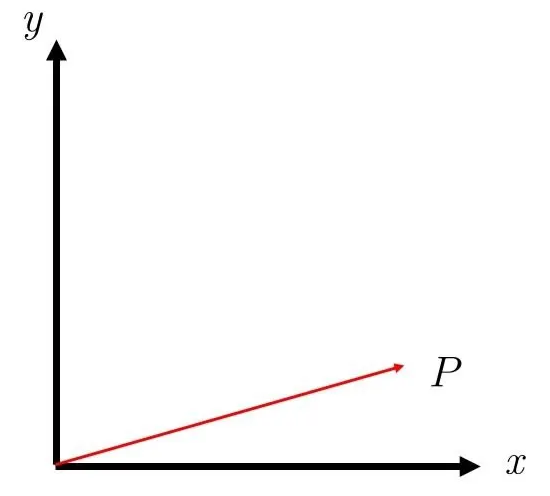
我们首先让它绕 Z 轴旋转一个角度 α:
P′=Rz(α) P
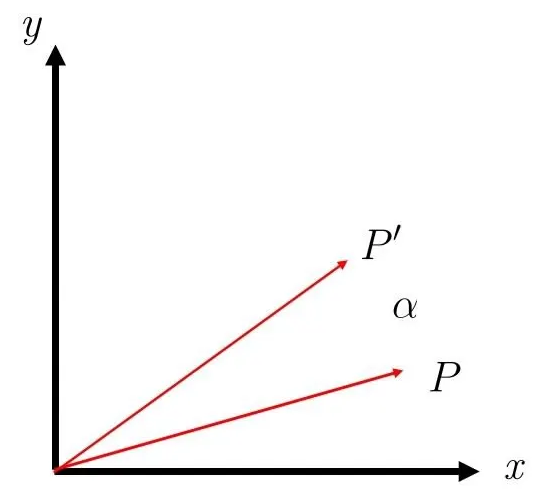
然后,我们再绕同一个固定的轴施加第二个旋转,旋转角度为 β :
P′′=Rz(β) P′
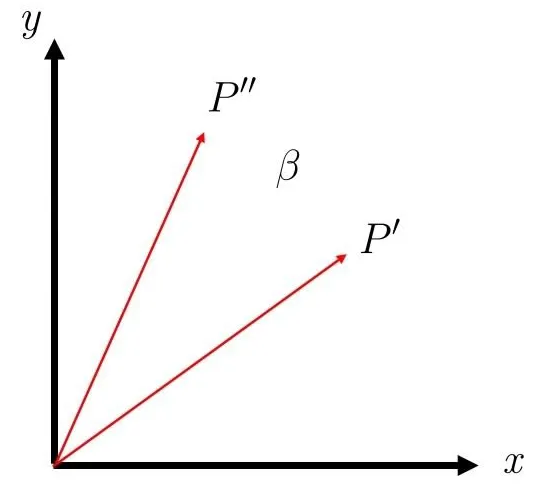
将第一个关系式代入第二个式子,可得
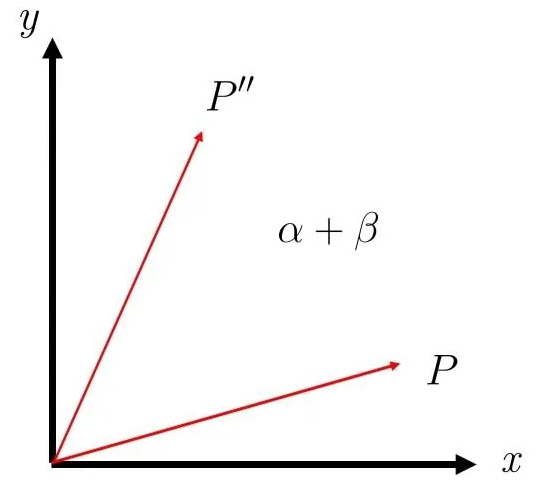
P′′=Rz(β)(Rz(α) P)=(Rz(β)Rz(α)) P
其中矩阵
Rtot=Rz(β)Rz(α)
代表了相对于同一个固定坐标系,这两个连续旋转组合后的总效果。
这里顺序非常重要:
当我们执行一系列绕固定坐标系的旋转时,总的旋转矩阵是通过"左乘"(前乘)各个旋转矩阵得到的,且矩阵的顺序与旋转发生的顺序一致。
我们可以在三维空间中应用同样的逻辑,只不过旋转轴各不相同。例如,如果我们先绕 z 轴旋转 α 角,再绕 y 轴旋转 β 角,最后绕 x 轴旋转 γ 角,且所有旋转都是相对于同一个固定坐标系进行的,那么总的旋转矩阵为:
Rtot=Rx(γ) Ry(β) Rz(α)
3. 为什么旋转顺序至关重要
三维旋转的一个关键特性是:
通常情况下,旋转操作是不可交换的。
先执行旋转 A 再执行旋转 B,其结果不等于先执行旋转 B 再执行旋转 A。
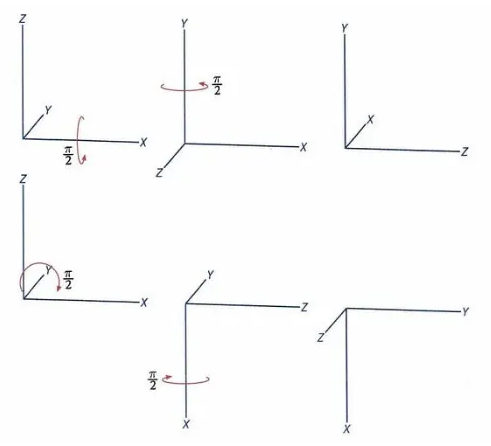
图片中用一个简单的例子展示了这一现象,即两次90°的旋转。
我们从同一个初始坐标系(X, Y, Z)开始:
上排:
-
绕 X 轴旋转 π/2。
-
然后绕 Y 轴旋转 π/2。
-
用矩阵符号表示,这一序列是:
-
R_total = Ry(π/2) Rx(π/2)
下排:
-
绕 Y 轴旋转 π/2。
-
然后绕 X 轴旋转 π/2。此时的序列是:R_total = Rx(π/2) Ry(π/2)
尽管我们使用的角度相同、涉及的轴也相同,但图片中两行的最终坐标系显然不同:标签 X、Y、Z 最终指向了完全不同的方向。
我们也可以直接通过矩阵计算来看出这一差异。利用绕 X 轴和 Y 轴的标准旋转矩阵:
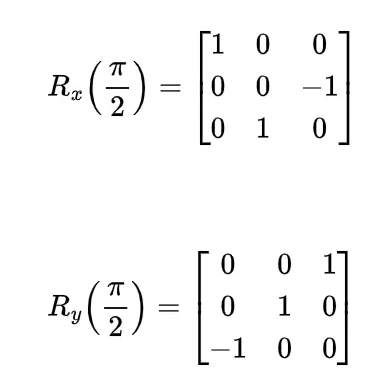
如果先绕 X 轴旋转,再绕 Y 轴旋转,总的旋转矩阵为
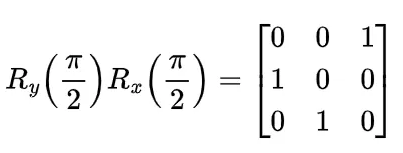
如果我们将顺序对调,先绕 Y 轴旋转,再绕 X 轴旋转,则得到
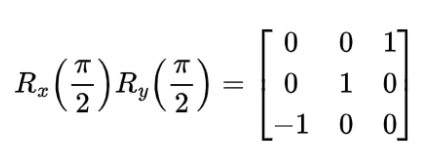
这两个矩阵并不相等,它们正好分别对应图中所示的两个不同的最终坐标系。
这就是为什么当我们写下类似
Rtot = Rx(γ) Ry(β) Rz(α)
这样的公式时,顺序至关重要。这个公式编码了一个精确的旋转序列:
首先绕 z 轴旋转角度 α ,
然后绕 y 轴旋转角度 β ,
最后绕 x 轴旋转角度 γ ,
(在本例中,所有旋转均相对于选定的固定坐标系进行)。
改变矩阵的相乘顺序,意味着改变了物体的实际运动路径,最终会导致机器人、相机或无人机的朝向完全不同。
4. 从旋转矩阵到三角度表示
旋转矩阵功能强大,但它们也存在冗余性:
-
一个三维旋转矩阵包含 9 个数值。
-
但由于矩阵的行和列必须满足标准正交(Orthonormal)条件,这带来了 6 个独立约束。
-
因此,真正剩下的自由度只有 3 个。
所以,尽管我们喜欢用矩阵来进行计算,但我们知道,实际上只要有 3 个独立参数就足以描述刚体在空间中的任意姿态了。用群论的语言来说,这就是三维旋转群 SO(3) 是一个三维空间的事实;一般来说, SO(m) 需要(m−1)/2 个参数。
这就引出了最小表示法的概念:
姿态的最小表示法,是指任何一组能够唯一地(除了一些奇异情况外)描述三维旋转的三个独立参数。
像欧拉角和横滚-俯仰-偏航角这样的三角度描述方法,就是此类最小表示法的典型例子。
5. 欧拉旋转定理
欧拉旋转定理为我们提供了理论基石:
欧拉旋转定理
任意两个相互独立的正交坐标系,都可以通过不超过三次绕坐标轴的旋转来相互对齐。其中,任意两个连续的旋转不能绕同一轴进行。
这一定理告诉我们:
-
我们总是可以通过最多三次基本旋转,来实现从一个坐标系到另一个坐标系的变换。
-
选择这三个旋转轴和对应角度的方式有很多。
如果我们仅限于绕 x、y、z 轴旋转,并且要求任意两个连续的旋转不能绕同一轴进行 ,那么我们一共可以得到 12 种合法的轴组合(例如 ZYZ、ZXZ、ZYX 等)。每一种组合定义了一种特定的欧拉角约定。
在机器人学和航空航天领域,有两种组合尤为常见:
- ZYZ 欧拉角
- ZYX 角(即横滚-俯仰-偏航角 / RPY)
接下来,我们将先从 ZYZ 角开始讲解,使用你之前已经见过的"当前坐标系视角"。
6. ZYZ 欧拉角(当前坐标系视角)
想象一下,你有一个初始坐标系 O--XYZ ,想要到达某个最终坐标系O--X‴Y‴Z‴。ZYZ 约定使用了三次旋转:
- 绕原始 Z 轴旋转一个角度 φφ 。
- 绕新的 Y 轴(通常记作Y′)旋转一个角度 θθ 。
- 绕第二次旋转后的新 Z 轴(通常记作Z″)旋转一个角度 ψψ 。
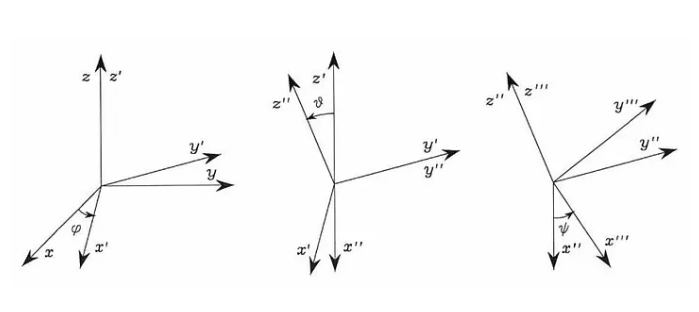
你可以通过三张图来展示这三个步骤:
- 步骤 1:绕 Z 轴旋转 φφ 后的坐标系。
- 步骤 2:绕 Y′ 轴旋转 θθ 后的坐标系。
- 步骤 3:绕 Z″ 轴旋转 ψψ 后的坐标系,即最终姿态。
因为每一次旋转都是相对于当前坐标系 定义的,所以总的旋转矩阵是通过基本旋转矩阵的右乘得到的:R = Rz(φ) Ry(θ) Rz(ψ)
R=Rz(φ)Ry(θ)Rz(ψ
其中:
-
Rz(φ)= 绕 Z 轴旋转角度 φ
-
Ry(θ)= 绕当前 Y 轴旋转角度 θ
-
Rz(ψ) = 绕当前 Z 轴旋转角度 ψ
如果你喜欢更紧凑的符号表示法,可以做如下简写:
-
cφ = cosφ, sφ = sinφ
-
cθ = cosθ, sθ = sinθ
-
cψ = cosψ, sψ = sinψ
然后,完整的矩阵 R 就可以写成:
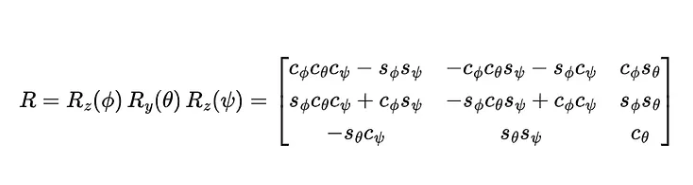
最重要的是不要死记硬背这个矩阵,而是要理解它的结构:
- 它仅仅是三个基本旋转矩阵的乘积。
- 矩阵的顺序与物理旋转顺序相对应:"先绕 Z 轴旋转,再绕 Y′ 轴旋转,最后绕 Z″ 轴旋转"。
- 如果改变这一顺序,就会得到一个完全不同的矩阵和最终姿态。
在实际应用中,ZYZ 角 经常被用于机器人机械臂,因为它们能很好地映射到球形手腕的结构上,或者适用于那些末端执行器需要绕工具轴达到某种对称姿态的问题。
什么是无监督学习?理解人工智能中无监督学习的机制、各类算法的类型与应用
7. ZYZ 角:逆问题
到目前为止,我们已经了解了如何从三个 ZYZ 角度(φ,θ,ψ)计算出旋转矩阵 RR。
但在实际应用中,我们经常面临相反的问题:
已知一个旋转矩阵 R ,我们该如何反推出角度θ, φ, ψ ?
这在本质上与逆运动学非常相似:我们不再是通过角度去计算姿态,而是希望通过姿态去反算出所需的角度。
假设 R 具有如下形式:
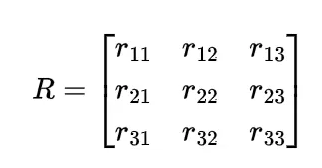
并假设它是通过以下公式生成的:R = Rz(φ) Ry(θ) Rz(ψ)
其中使用了紧凑的符号表示法:
cφ = cosφ, sφ = sinφ, cθ = cosθ, sθ = sinθ, cψ = cosψ, sψ = sinψ
从上述公式的显式矩阵表达式(即等式右边的部分)中,我们特别可以看出:
r₁₃ = cφ sθ
r₂₃ = sφ sθ
r₃₃ = cθ
r₃₁ = −sθ cψ
r₃₂ = sθ sψ
这些矩阵元素仅包含一个或两个角度,这使得它们非常适合用于反推求解。
7.1 一般情况: sθ ≠ 0 (θ ∈ (0, π))
首先假设 sθ≠0sθ ≠ 0sθ=0,即 θ 不等于 0 或 π 。这是没有奇异性的"常规"情况。
- 从 (1,3) 和 (2,3) 位置的元素反推 φ 由
φ = Atan2(r₂₃, r₁₃)和r₁₃ = cφ sθ 可得 tanφ = r₂₃ / r₁₃ 为了正确处理所有四个象限,我们使用双参数反正切函数:φ = Atan2(r₂₃, r₁₃)
(注: Atan2(y,x) 返回一个角度,该角度的余弦-正弦对分量为 (x,y) ,并会自动跟踪符号。)
-
从同一列反推 θ 依然根据
r₁₃ = cφ sθ,r₂₃ = sφ sθ以及 r₃₃ = cθ,我们得到r₁₃² + r₂₃² = (cφ² + sφ²) sθ² = sθ² 所以 sθ = √(r₁₃² + r₂₃²) cθ = r₃₃ 再次使用 Atan2 函数,并将 θ 限定在 (0,π) 范围内:θ = Atan2( √(r₁₃² + r₂₃²), r₃₃ ) -
从最后一行反推 ψ 由 r₃₁ = −sθ cψ 和 r₃₂ = sθ sψ 可得
tanψ = r₃₂ / (−r₃₁)
因此
ψ = Atan2( r₃₂, −r₃₁ )
综上所述,在一般情况 sθ≠0 and θ ∈ (0, π) 且
φ = Atan2( r₂₃, r₁₃ )θ = Atan2( √(r₁₃² + r₂₃²), r₃₃ ) 其中 θ ∈ (0, π)ψ = Atan2( r₃₂, −r₃₁ )
这些公式接收一个已知由 ZYZ 角生成的旋转矩阵 (φ, θ, ψ) 。
7.2 第二组解(多解分支)
由于三角函数具有周期性且不是一一对应的,通常会有多个有效的角度三元组对应同一个矩阵 R 。可以通过将 θ 取在区间 (−π,0) 而非 (0,π) 来获得第二组解。一种方便的写法是:
φ = Atan2( −r₂₃, −r₁₃ )θ = Atan2( −√(r₁₃² + r₂₃²), r₃₃ ) 其中 θ ∈ (−π, 0)ψ = Atan2( −r₃₂, r₃₁ )
你可以通过代入验证,将这两个分支代入公式 R = Rz(φ) Ry(θ) Rz(ψ)后,都会产生相同的矩阵 R 。
在实际应用中(例如机械臂手腕的逆运动学),我们通常会使用额外的判据来选择使用哪个分支:例如关节角度限制、与上一时刻解的连续性,或者运动量最小化原则。
7.3 奇异情况: θ=0 或 θ=π (类似万向节的退化)
上述公式假设了sθ≠0 。如果 sθ=0,则 θ 为 0 或 π ,此时几个关键的矩阵元素变为零:
r₁₃ = cφ sθ = 0r₂₃ = sφ sθ = 0r₃₁ = −sθ cψ = 0r₃₂ = sθ sψ = 0r₃₃ = cθ = ±1
此时,矩阵 R 简化为
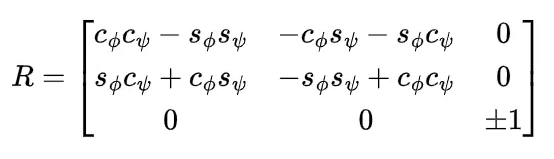
在这种情况下, φ 和 ψ 只会以角度的和(或差)的形式出现,因此它们不再能被唯一确定:许多不同的 (φ, ψ) 组合都会产生同一个矩阵 RR 。
这是 ZYZ 欧拉角的一个典型奇异点(类似于万向节死锁):当中间的角度 θ 为 0 或 π 时,第一次和第三次旋转会变得无法区分(因为它们实际上变成了绕同一轴的旋转)。在实际应用中,通常的做法是:
- 通过 r33=cθ 确定 θ=0 (或 π ),
- 设定 φ=0 ,让 ψ 承担全部旋转量,或者反过来,
- 或者利用应用中的额外信息来选择一个合适的 (φ,ψ) 组合。
有了这些公式,你现在就掌握了完整的双向转换:
- 正向问题:从 (φ,θ,ψ) 到R ,通过公式 R=Rz(φ)Ry(θ)Rz(ψ)
- 逆向问题:从 R 回到 (φ,θ,ψ) ,同时处理了一般情况和奇异情况。
8. 横滚-俯仰-偏航角
在机器人学和航空航天领域,姿态通常使用横滚-俯仰-偏航角来描述。这其实就是一种特定的 ZYX 约定:
横滚-俯仰-偏航角是代表绕固定坐标系旋转的 ZYX 角(即使用左乘/前乘规则)。
使用通常的命名习惯:
- ψ = 横滚(Roll,绕 X 轴的旋转)
- θ = 俯仰(Pitch,绕 Y 轴的旋转)
- φ = 偏航(Yaw,绕 Z 轴的旋转)
按照绕固定坐标系旋转的顺序,步骤如下:
- 绕固定的 X 轴旋转 ψ 角 → Rx(ψ)
- 绕固定的 Y 轴旋转 θ 角 → Ry(θ)
- 绕固定的 Z 轴旋转 φ 角 → Rz(φ)
由于这些旋转都是相对于固定坐标系定义的,因此总的旋转矩阵为:
R = Rz(φ) Ry(θ) Rx(ψ)
如果我们使用简写符号 cφ = cosφ, sφ = sinφ, cθ = cosθ, sθ = sinθ, cψ = cosψ, sψ = sinψ, 那么完整的矩阵形式为
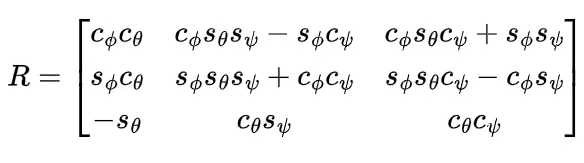
同样的,核心思想与 ZYZ 角度是一致的:
-
这个矩阵仅仅是三个简单旋转的乘积,
-
其顺序编码了围绕 z、y、x 轴的确切 RPY 序列,
-
改变顺序就会改变最终生成的姿态。
- 滚转-俯仰-偏航角的逆问题
就像 ZYZ 角度一样,在实际应用中,我们通常已知旋转矩阵 R ,并希望反推出角度 (ϕ,θ,ψ) 。
写成
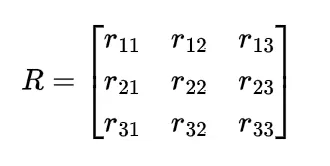
并假设它通过 RPY 角度由公式 R = Rz(φ) Ry(θ) Rx(ψ) 得出。
从上面的显式表达式中,我们可以读取一些有用的矩阵元素:
r₃₁ = −sθr₃₂ = cθ sψr₃₃ = cθ cψr₂₁ = sφ cθr₁₁ = cφ cθ
9.1 一般情况: cθ ≠ 0
如果 cθ ≠ 0(即 θ 不等于 ±π/2 ),提取角度的过程是直接的:
φ = Atan2( r₂₁, r₁₁ )θ = Atan2( −r₃₁, √(r₃₂² + r₃₃²) ) 其中 θ ∈ (−π/2, π/2)ψ = Atan2( r₃₂, r₃₃ )
对于给定的旋转矩阵 R ,这给出了一组一致的三元组 (ϕ,θ,ψ) 。
由于三角函数具有周期性,存在第二个有效的解分支;一种方便的形式是:
φ = Atan2( −r₂₁, −r₁₁ )θ = Atan2( −r₃₁, −√(r₃₂² + r₃₃²) ) 其中 θ ∈ (π/2, 3π/2)ψ = Atan2( −r₃₂, −r₃₃ )
当将这两个分支代回公式 R = Rz(φ) Ry(θ) Rx(ψ) 时,它们对应相同的 R ;在实际应用中,我们通常选择最符合关节限制或连续性要求的那个解。
9.2 奇异情况: cosθ=0 (类似万向节的退化)
当 cosθ=0 时,俯仰角 θ 为 ±π/2 ,上述表达式变得奇异:只有 ϕ 和 ψ 的和或差被唯一确定。
从几何上看,这与 ZYZ 角度中看到的"万向节锁"现象相同:两个旋转轴对齐,导致角度三元组丢失部分信息。在实践中,通常采取以下方法之一:
-
根据 r₃₁ 确定 θ=±π/2 ;
-
将 ϕ 和 ψ 合并为一个有效的偏航/滚转角;
-
或者在这些奇点附近切换到其他表示形式(例如四元数)。
结论
在本系列的第三部分中,我们从单一旋转过渡到了由多个旋转和三个角度构建的完整 3D 姿态描述。
首先,我们看到了旋转矩阵是如何组合的:
-
在当前坐标系(current-frame)视角下,我们通过 Pⁱ = Rʲⁱ Pʲ 和类似 的乘积来连接坐标系。
-
这是机器人手臂正向运动学的语言:我们通过后乘(post-multiplying)连续坐标系之间的旋转,从基座走到末端执行器。
-
在固定坐标系(fixed-frame)视角下,我们保持一个坐标系静止,并对同一个向量应用多次旋转,乘积形式如 P″ = Rz(β) Rz(α) P 。
-
在这里,旋转是按应用顺序前乘(pre-multiplied)的。
通过使用 Rx(π/2) 和 Ry(π/2) 的简单示例,我们明确了旋转不满足交换律:改变顺序会改变最终姿态。这就是为什么像 R_tot = Rx(γ) Ry(β) Rz(α) 这样的表达式中,因子的顺序具有真实的几何意义。
接下来,我们介绍了三角度表示法:
-
ZYZ 欧拉角 (ϕ,θ,ψ) ,在当前坐标系视角下构建为 R = Rz(φ) Ry(θ) Rz(ψ)。
-
我们写出了完整的矩阵,然后解决了逆问题,从 R 的元素中反推出 (ϕ,θ,ψ) ,包括常规情况和奇异(类似万向节锁)情况。
-
滚转-俯仰-偏航角(RPY),解释为固定坐标系视角下的 ZYX 约定:R = Rz(φ) Ry(θ) Rx(ψ) 。
同样,我们推导了正向矩阵和逆公式,并观察到当俯仰角 θ 达到 ±π/2 时,奇异点是如何出现的。
贯穿所有这些内容,有几个关键思想反复出现:
-
无论我们用矩阵还是角度来描述,3D 姿态只有三个自由度。
-
旋转矩阵非常适合计算和组合;而角度三元组(欧拉角、RPY)非常适合人类直觉和指定指令。
-
约定的选择(ZYZ、ZYX、当前坐标系、固定坐标系)以及乘积中因子的顺序至关重要------它们编码了实际的物理运动。
通过第 I 至 III 部分,你现在拥有了一个完整的工具包来思考机器人学中的旋转问题:
-
坐标系和旋转矩阵
-
坐标变换和向量旋转
-
旋转的组合
-
两种最常见的三角度参数化方法及其逆映射
在后续的学习中,你可以在此基础上进一步探索四元数、完整的齐次变换(旋转 + 平移),以及最终真实机器人手臂的完整正向和逆向运动学。