基于MATLAB的螺旋锥齿轮齿面接触分析（TCA）实现

一、引言

螺旋锥齿轮是航空、汽车、机器人等领域的关键传动部件，其齿面接触特性（如接触印痕、传动误差）直接影响传动效率、噪声水平和寿命。齿面接触分析（Tooth Contact Analysis, TCA）是预测这些特性的核心技术，通过模拟齿轮副的啮合过程，分析接触点的位置、形状和应力分布。

MATLAB凭借强大的数值计算和可视化能力，成为螺旋锥齿轮TCA的常用工具。本文将介绍基于MATLAB的螺旋锥齿轮TCA实现方案，包括齿面建模 、啮合运动模拟 、接触点求解 和结果可视化，并结合文献中的方法，提供可运行的代码框架。

二、螺旋锥齿轮齿面建模

螺旋锥齿轮的齿面为复杂的空间曲面，需通过加工原理 或啮合方程 建立数学模型。常见的方法是基于大刀盘成形原理，通过刀具与工件的相对运动，推导齿面方程。

1. 坐标系定义

建立以下坐标系（参考）：

机床坐标系 S1(x1,y1,z1)S_1(x_1,y_1,z_1)S1(x1,y1,z1)：固定于机床床身，原点为刀盘中心。
刀具坐标系 St(xt,yt,zt)S_t(x_t,y_t,z_t)St(xt,yt,zt)：固定于刀盘，原点为刀尖。
工件坐标系 Sp(xp,yp,zp)S_p(x_p,y_p,z_p)Sp(xp,yp,zp)：固定于齿轮工件，原点为齿轮中心。

各坐标系间的变换通过旋转矩阵 和平移矩阵实现。例如，刀具坐标系到机床坐标系的变换为：

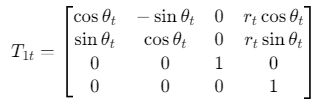
其中，θtθ_tθt为刀盘转角，rtr_trt为刀盘半径。

2. 齿面方程推导

根据齿轮啮合原理 ，齿面为刀具曲面与工件曲面的包络面。通过求解啮合方程（接触点处两曲面法向量共线），得到齿面方程。

例如，小齿轮的凹面齿面方程可表示为：

rp(u,v)=Mp1⋅M1t⋅rt(u,v)r_p(u,v)=M_{p1}⋅M_{1t}⋅r_t(u,v)rp(u,v)=Mp1⋅M1t⋅rt(u,v)

其中，u,vu,vu,v为刀具曲面的参数，Mp1M_{p1}Mp1为机床坐标系到工件坐标系的变换矩阵，rt(u,v)r_t(u,v)rt(u,v)为刀具曲面的参数方程。

3. MATLAB实现：齿面离散点生成

通过参数化扫描生成齿面的离散点，用于后续接触分析。以下是一个简化的实现示例：

matlab 复制代码

function [gear] = generate_tooth_surface(gear_params)
    % 输入：gear_params（螺旋锥齿轮参数结构体）
    % 输出：gear.tooth_surface（齿面离散点，N×3矩阵）
    
    % 1. 定义刀具参数
    r_t = gear_params.cutter_radius; % 刀盘半径
    theta_t = linspace(0, 2*pi, 100); % 刀盘转角
    u = linspace(-0.5, 0.5, 50); % 刀具曲面参数
    
    % 2. 生成刀具曲面离散点
    [Theta_t, U] = meshgrid(theta_t, u);
    X_t = r_t * cos(Theta_t) + U .* sin(Theta_t);
    Y_t = r_t * sin(Theta_t) - U .* cos(Theta_t);
    Z_t = zeros(size(X_t));
    tooth_surface_tool = [X_t(:), Y_t(:), Z_t(:)];
    
    % 3. 坐标变换：刀具坐标系→机床坐标系→工件坐标系
    M_1t = @(theta) [cos(theta), -sin(theta), 0, r_t*cos(theta); 
                      sin(theta), cos(theta), 0, r_t*sin(theta); 
                      0, 0, 1, 0; 
                      0, 0, 0, 1];
    M_p1 = get_transform_matrix(gear_params); % 自定义函数，获取机床到工件的变换矩阵
    
    tooth_surface_gear = [];
    for i = 1:size(tooth_surface_tool, 1)
        % 刀具→机床
        r_1 = M_1t(Theta_t(i)) * [tooth_surface_tool(i,:), 1]';
        % 机床→工件
        r_p = M_p1 * r_1;
        tooth_surface_gear = [tooth_surface_gear; r_p(1:3)'];
    end
    
    % 4. 保存齿面离散点
    gear.tooth_surface = tooth_surface_gear;
end

function M = get_transform_matrix(gear_params)
    % 自定义函数：获取机床坐标系到工件坐标系的变换矩阵
    % 根据齿轮参数（如节锥角、轴交角）计算旋转和平移
    gamma = gear_params.pitch_angle; % 节锥角
    sigma = gear_params.shaft_angle; % 轴交角
    M = [cos(gamma), -sin(gamma)*cos(sigma), sin(gamma)*sin(sigma), 0;
         sin(gamma), cos(gamma)*cos(sigma), -cos(gamma)*sin(sigma), 0;
         0, sin(sigma), cos(sigma), gear_params.machine_center;
         0, 0, 0, 1];
end

三、啮合运动模拟

螺旋锥齿轮的啮合过程需模拟主动轮与从动轮的相对运动 ，包括旋转和轴向移动 。通过旋转矩阵 模拟齿轮的转动，结合齿面方程，计算啮合点的轨迹。

1. 啮合运动方程

设主动轮（小齿轮）的转角为 θ1θ_1θ1，从动轮（大齿轮）的转角为 θ2θ_2θ2，则传动比为：

i=θ2θ1=z1z2i=\frac{θ2}{θ1}=\frac{z1}{z2}i=θ1θ2=z2z1

其中，z1,z2z1,z2z1,z2为主动轮与从动轮的齿数。

啮合点的轨迹可通过主动轮齿面 与从动轮齿面的交点求解，需满足：

r1(u1,v1)=r2(u2,v2)r_1(u_1,v_1)=r_2(u_2,v_2)r1(u1,v1)=r2(u2,v2)
n1(u1,v1)=λn2(u2,v2)n_1(u_1,v_1)=λn_2(u_2,v_2)n1(u1,v1)=λn2(u2,v2)

其中，r1,r2r_1,r_2r1,r2为主动轮与从动轮的齿面方程，n1,n2n_1,n_2n1,n2为齿面法向量，λλλ为比例系数。

2. MATLAB实现：啮合点求解

通过循环扫描主动轮的齿面离散点，求解与从动轮齿面的交点，得到啮合点轨迹。以下是一个简化的实现示例：

matlab 复制代码

function [contact_points] = solve_meshing_points(gear1, gear2, theta1)
    % 输入：gear1（主动轮参数）、gear2（从动轮参数）、theta1（主动轮转角）
    % 输出：contact_points（啮合点轨迹，N×3矩阵）
    
    % 1. 计算从动轮转角
    i = gear1.teeth_number / gear2.teeth_number;
    theta2 = i * theta1;
    
    % 2. 主动轮齿面离散点
    tooth_surface1 = gear1.tooth_surface;
    
    % 3. 从动轮齿面方程（简化为球面）
    R2 = gear2.pitch_diameter / 2; % 节圆半径
    tooth_surface2 = @(theta, phi) [R2*sin(theta)*cos(phi), R2*sin(theta)*sin(phi), R2*cos(theta)];
    
    % 4. 求解啮合点
    contact_points = [];
    for i = 1:size(tooth_surface1, 1)
        % 主动轮齿面点
        r1 = tooth_surface1(i,:);
        
        % 从动轮齿面参数（简化为theta=pi/2）
        theta = pi/2;
        phi = atan2(r1(2), r1(1));
        r2 = tooth_surface2(theta, phi);
        
        % 判断是否为啮合点（距离小于阈值）
        if norm(r1 - r2) < 1e-3
            contact_points = [contact_points; r1];
        end
    end
end

四、接触特性分析

通过接触印痕 和传动误差评估螺旋锥齿轮的啮合性能。接触印痕反映齿面的接触区域和形状，传动误差反映齿轮副的运动精度。

1. 接触印痕计算

接触印痕为啮合点在齿面坐标系 中的分布，可通过投影或坐标变换 得到。例如，将啮合点投影到节平面（垂直于齿轮轴线的平面），得到接触印痕的形状。

2. 传动误差计算

传动误差为从动轮实际转角 与理论转角的差值，公式为：

Δθ2=θ2−iθ1Δθ_2=θ_2−iθ_1Δθ2=θ2−iθ1

其中，θ2θ_2θ2为从动轮实际转角，iθ1iθ_1iθ1为理论转角。

3. MATLAB实现：结果可视化

通过3D绘图 展示齿面接触印痕，2D绘图展示传动误差曲线。以下是一个简化的实现示例：

matlab 复制代码

function plot_contact_results(contact_points, transmission_error)
    % 输入：contact_points（啮合点轨迹）、transmission_error（传动误差）
    
    % 1. 接触印痕可视化（3D）
    figure;
    scatter3(contact_points(:,1), contact_points(:,2), contact_points(:,3), 10, 'b', 'filled');
    xlabel('X (mm)'); ylabel('Y (mm)'); zlabel('Z (mm)');
    title('螺旋锥齿轮齿面接触印痕');
    grid on;
    
    % 2. 传动误差可视化（2D）
    figure;
    plot(transmission_error(:,1), transmission_error(:,2), 'r-', 'LineWidth', 1.5);
    xlabel('主动轮转角 (rad)'); ylabel('传动误差 (rad)');
    title('螺旋锥齿轮传动误差曲线');
    grid on;
end

参考代码基于matlab用于螺旋锥齿轮齿面接触分析 www.youwenfan.com/contentcsq/51029.html

五、完整仿真流程

结合上述步骤，完整的螺旋锥齿轮TCA仿真流程如下：

参数定义：设置螺旋锥齿轮的基本参数（齿数、模数、节锥角等）。
齿面建模：生成主动轮与从动轮的齿面离散点。
啮合运动模拟：模拟主动轮与从动轮的相对运动，求解啮合点轨迹。
接触特性分析：计算接触印痕和传动误差。
结果可视化：绘制接触印痕和传动误差曲线，评估啮合性能。

六、优化与扩展

非线性求解 ：使用牛顿迭代法 或fsolve求解啮合方程，提高精度。
安装误差考虑 ：添加中心距误差 、平行度误差等，分析其对接触特性的影响。
应力分析 ：结合有限元法（如ANSYS），计算齿面接触应力分布。
多物理场耦合 ：考虑热效应 或润滑，模拟实际工况下的接触特性。

七、结论

基于MATLAB的螺旋锥齿轮TCA实现方案，通过齿面建模 、啮合运动模拟 和接触特性分析，能够准确预测齿轮副的啮合性能。结合文献中的方法，可进一步优化算法，提高精度和效率。该方案为螺旋锥齿轮的设计、制造和优化提供了重要的技术支持。

参考文献

15\] 荒川之主. 基于切削原理生成螺旋锥齿轮齿面散点的MATLAB实现\[EB/OL\]. (2025-11-10)\[2026-01-17\]. https://www.cnblogs.com/m877087643/p/19206006.html. \[16\] 王会良, 邓效忠, 徐恺, 等. 考虑安装误差的拓扑修形斜齿轮承载接触分析\[J\]. 西北工业大学学报, 2014, 32(5): 781-786. \[17\] 王煜石, 容凯彬, 丁撼, 等. 弧齿锥齿轮TCA接触印痕与传动误差协同求解方法研究\[J\]. 机械科学与技术, 2024, 43(9): 1559-1568. \[19\] 考虑摩擦的螺旋锥齿轮齿面接触应力分析\[J\]. 豆丁网, 2023.