访问大角几何官网(https://dajiaoai.com/)
在数学教学的数字化转型中,大角几何Beta版的函数图像绘制功能摒弃了华而不实的"自动魔法",将数学严谨性置于首位,让教师重拾对可视化过程的完全掌控。
数学可视化的十字路口:自动便捷与教学严谨的抉择
当前数学教学工具大多面临一个根本性矛盾:是追求"一键生成"的便捷性,还是坚守数学呈现的严谨性?许多号称智能的工具通过自动化简化了操作,却常常在数学细节上做出妥协------自动取整导致的坐标偏移、算法优化形成的图像畸变、预设模板带来的表达限制。这些微小偏差在专业教师眼中尤为刺眼,可能误导学生对数学概念的精确理解。
大角几何Beta版选择了截然不同的道路。它不追求表面的自动化魔法,而是深入数学教学的本质需求,打造了一个既直观又精确的可视化环境。在这里,每一个像素都经过严谨的数学计算,每一次呈现都忠实于函数表达式。
大角几何Beta版:数学严谨性的技术实现
精确渲染引擎:从表达式到图像的零误差转换
大角几何的代数面板接受函数输入后,其核心算法确保了从数学表达式到视觉图像的精确转换:
关键特性:
-
自适应采样算法:根据函数特性动态调整采样密度,在曲率大的区域自动增加采样点,保证图像平滑;在近似线性区域减少采样点,提升渲染效率。
-
数学精确计算:避免浮点数误差积累,确保关键点(零点、极值点、不连续点)位置精确。
-
无限缩放支持:保持数学比例一致性,放大缩小过程中不损失精度,满足微观与宏观观察需求。
教学应用示例:
输入函数y=sin(1/x),大角几何在x=0附近自动增加采样点,清晰展示函数在这一区域的振荡特性,而许多简化工具会因采样不足而产生误导性平滑图像。
表达式解析的数学完整性
大角几何的代数引擎支持广泛的函数类型和表达形式:
支持的函数类别:
-
多项式与有理函数
-
三角函数及其反函数
-
指数与对数函数
-
隐函数表达式(如圆锥曲线方程)
严谨性体现:
对于函数y=sqrt(x),系统自动限制定义域为x≥0;对于y=1/x,在x=0处正确处理渐近线行为。这种对定义域和特殊点的精确处理,是数学严谨性的直接体现。
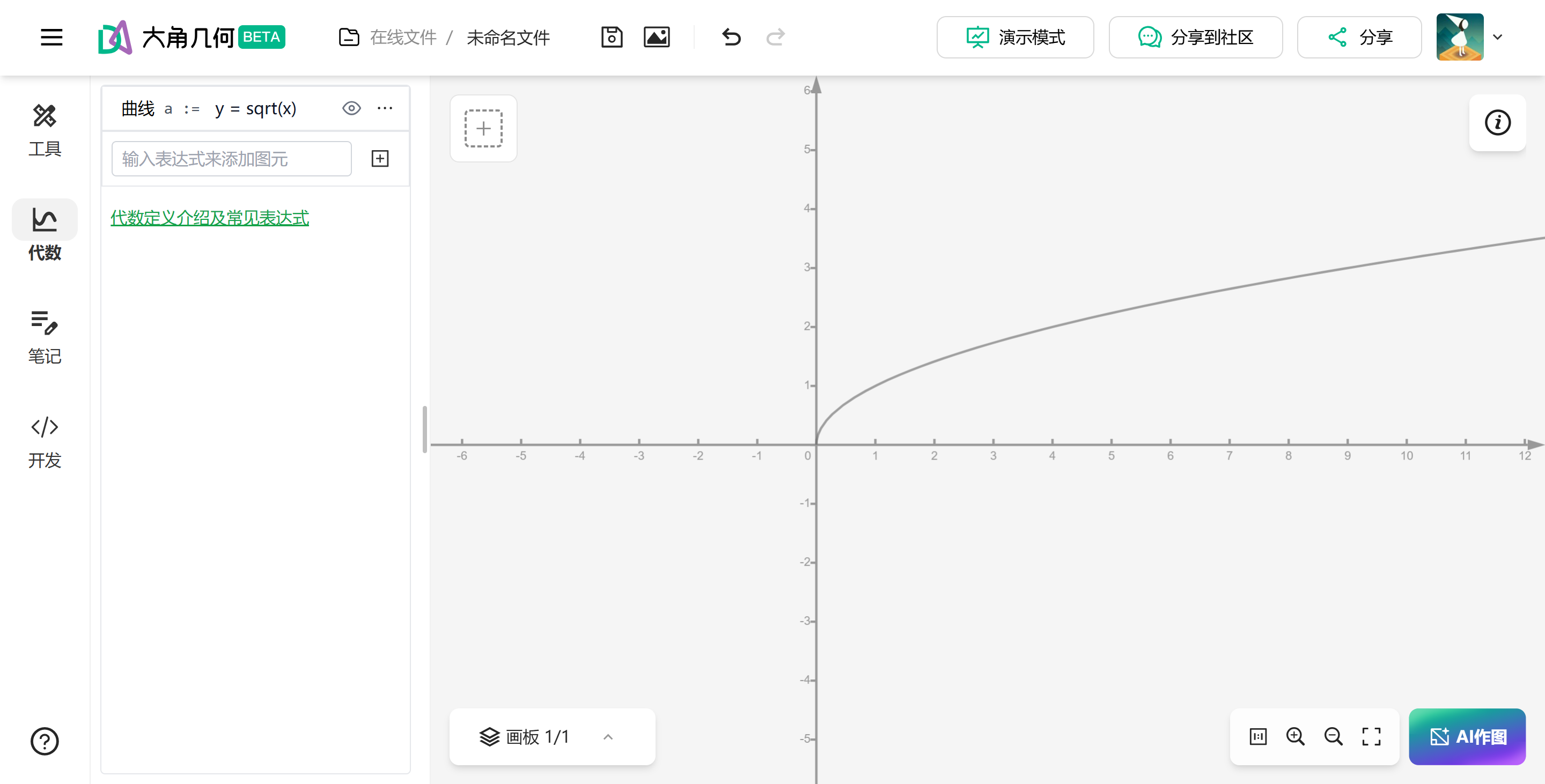
教学场景深度应用:严谨性如何提升教学效果
场景一:函数极限的直观教学
传统教学中,极限是学生最难建立直观理解的概念之一。大角几何Beta版通过精确的可视化提供了突破这一难点的工具:
教学步骤:
-
绘制函数
y=sin(x)/x -
观察函数在x=0附近的行为(虽然函数在x=0处未定义)
-
添加动点从两侧趋近于0
-
手动添加标注说明极限值为1
这种基于精确图像的直观展示,比纯代数推导更容易帮助学生建立极限概念的直觉理解。
场景二:函数变换的精确分析
函数变换是高中数学的核心内容,细微差别可能导致完全不同的函数性质:
大角几何能精确呈现这两种表达方式对应的图像生成逻辑,帮助学生理解形式不同但本质相同的数学表达。
场景三:探索数学猜想与反例
数学学习不仅是接受已知结论,更是探索未知可能:
教学应用:
学生提出猜想:"所有可导函数都是连续的。"教师可快速绘制函数y=x²·sin(1/x)(补充定义x=0时y=0),展示这是一个处处可导但导数不连续的函数,作为反例。这种即时的可视化验证,极大促进了学生的探究性学习。
从精确工具到数学思维培养
大角几何Beta版的价值远不止于生成图像,更在于通过精确可视化促进学生数学思维的发展:
培养数学表达的严谨性
当学生看到数学表达式中的每一个符号变化都对应图像的确切改变时,他们自然学会关注数学表达的精确性。一个正负号的差异、一个括号的位置、一个系数的变化,都会在图像中清晰体现。
建立数学直觉与形式证明的桥梁
精确可视化帮助学生将形式证明与几何直觉联系起来。例如,中值定理的证明过程可以通过函数图像上弦与切线的可视化得到直观支持,使抽象证明变得具体可感。
促进数学发现的乐趣
当学生能够即时看到自己构造的数学表达式的图像时,数学探索的反馈周期大大缩短。他们可以尝试各种函数组合,观察产生的效果,体验数学创造的乐趣。
教师角色的转变:从技术操作员到数学引导者
大角几何Beta版将教师从繁琐的技术操作中解放出来,使其能够专注于数学教学的本质:
课前准备阶段
教师不再花费大量时间调整自动化工具产生的瑕疵,而是专注于选择最合适的函数案例,设计最能揭示数学本质的可视化方案。
课堂实施阶段
教师可以根据学生反应即时调整可视化策略,快速响应课堂生成性问题。当学生提出未曾预料的问题时,教师可以现场输入函数表达式,即时生成精确图像进行探讨。
课后反思阶段
教学过程中生成的函数图像可以轻松保存、整理,形成具有个人特色的教学资源库,这些资源因其数学精确性而具有长期使用价值。
对比分析:严谨性优先的设计哲学
| 对比维度 | 大角几何Beta版 | 常见自动化工具 |
|---|---|---|
| 图像精确度 | 数学精确,忠实于表达式 | 常有近似处理,可能产生视觉误导 |
| 特殊点处理 | 正确处理定义域、不连续点等 | 常简化处理或忽略 |
| 用户控制 | 完全控制可视化每个环节 | 自动化预设,调整空间有限 |
| 学习曲线 | 需要理解数学逻辑 | 操作简单但理解受限 |
| 教学深度 | 支持深入数学探讨 | 适合基础展示 |
| 资源复用性 | 高,数学内容不过时 | 依赖特定模板,易过时 |
实践建议:最大化严谨性工具的教学价值
函数选择策略
-
典型代表函数:选择最能体现一类函数共性的代表
-
边界情况函数:包含定义域边界、不连续点等特殊情况
-
对比组函数:形成对比,突出特定性质差异
课堂呈现技巧
-
渐进式展示:先展示基础函数,再逐步添加复杂元素
-
问题引导:基于图像提出引导性问题,激发学生思考
-
学生参与:邀请学生提供函数表达式,即时可视化
资源建设方法
-
按主题分类:将函数图像按数学主题整理
-
标注关键特征:在图像上标注关键数学特征
-
添加教学笔记:记录每个图像的教学使用经验
数学教学技术的未来:走向深度而非表面
大角几何Beta版代表了数学教学工具发展的一个方向:从追求表面的便捷性转向深度的教育价值。这种转变反映了对数学教学本质的深刻理解------数学学习不仅是获取知识,更是发展思维;数学工具不仅是节省时间,更是提升理解。
未来,我们期待更多像大角几何这样的工具,它们不过度承诺"自动化魔法",而是扎实提供"精确工具";它们不试图替代教师的专业判断,而是增强教师的数学表达能力。在这样的工具辅助下,数学教学将更加深入、更加精确、更加激发思考。
结语:让数学回归严谨,让教学回归本质
在技术快速发展的时代,数学教学面临着诸多诱惑------炫目的动画、自动的生成、智能的推荐。然而,数学的本质是严谨,教学的灵魂是引导。大角几何Beta版通过提供数学精确的可视化功能,帮助我们在这个纷繁的技术环境中保持清醒:最好的教学工具不是替代思考的自动化机器,而是延伸思维的精确放大器。
当一位教师能够信任工具呈现的每一个数学细节时,他便可以全身心投入于教学的真正核心------引导学生思考、激发学生探索、培养学生对数学严谨之美的欣赏。
访问大角几何官网(https://dajiaoai.com/),体验数学严谨性与教学实用性完美结合的函数可视化工具。在这里,每一个像素都是数学真理的忠实呈现,每一次操作都是教学艺术的自由表达。